본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

• 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
  • IDE : IntelliJ IDEA (Ultimate Edition)
  • Java : JDK 21 (corretto-21)
  • Python : 3.9 (conda env)

[알고리즘] 정렬(Sorting) - Bubble Sort & Selection Sort

• 정렬 알고리즘의 전반적인 개요와 분류는 다음 포스팅에서 확인하실 수 있습니다.
  • [알고리즘] 정렬(Sorting) - 개요 (Java와 Python의 주요 정렬 방식 소개)

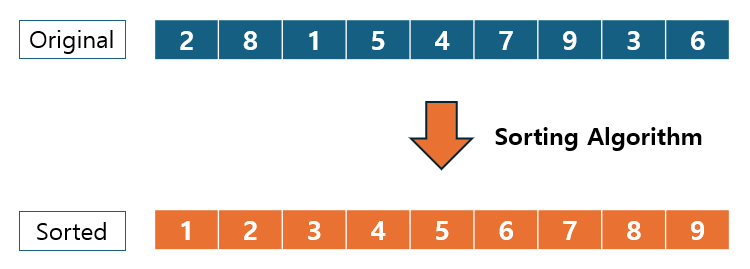
1. 단순 정렬 (Basic Sorting)

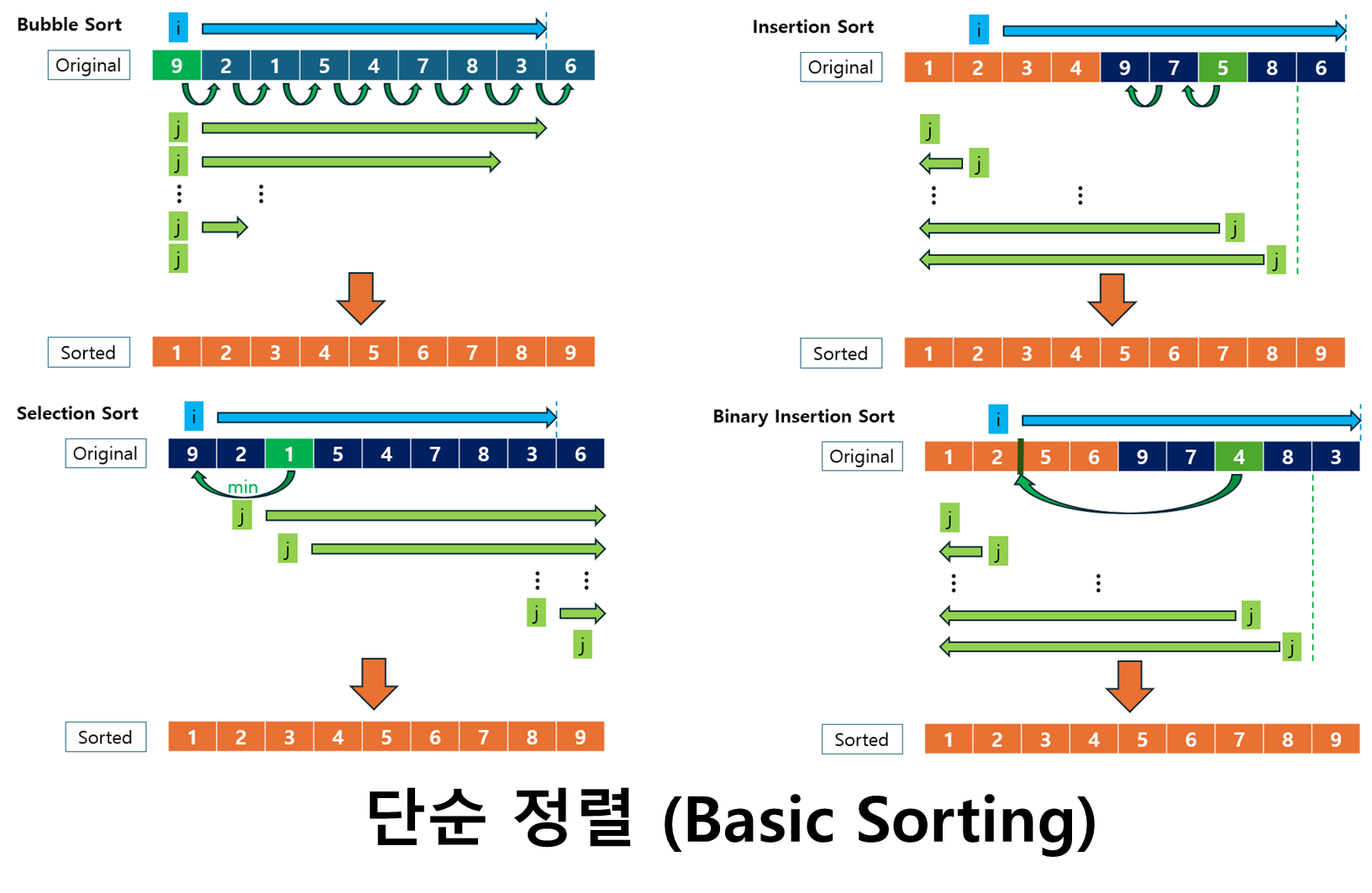
단순 정렬(Basic Sorting) 알고리즘은 기본적인 정렬 방식으로, 구현이 간단하고 상대적으로 이해하기 쉽습니다.

• 주로 데이터 크기가 작거나, 이미 정렬된 데이터에 대해 사용될 수 있습니다.
• 그러나 대부분의 경우 시간 복잡도가 $O(n^2)$로 비효율적이기 때문에, 대규모 데이터에서는 잘 사용되지 않습니다.

단순 정렬 알고리즘은 비교 기반 정렬로, 배열이나 리스트의 요소를 차례로 비교하며 정렬을 수행합니다.

• 각 알고리즘은 비교적 간단한 동작 원리를 기반으로 하기 때문에, 이해하기 쉽고 초보자에게 적합합니다.

대표적인 단순 정렬 알고리즘으로는 버블 정렬 (Bubble Sort), 선택 정렬 (Selection Sort), 삽입 정렬 (Insertion Sort) 등이 있으며, 이들은 주로 교육용이나 작은 데이터셋에 적합합니다.

• 이번 포스팅에서는 버블 정렬과 선택 정렬을 다루며, 다음 포스팅에서 삽입 정렬과 이진 삽입 정렬을 다룰 예정입니다.

다만, 실무 관점에서는 이 중에서 가장 중요하다 여겨지는 알고리즘은 삽입 정렬 (Insertion Sort)이라 볼수 있습니다.

• 다양한 프로그래밍 언어에서 일반적으로 작은 길이의 데이터에 대한 표준 정렬 알고리즘으로 가장 많이 쓰이는 방식이기 때문입니다.

2. Bubble Sort (버블 정렬)

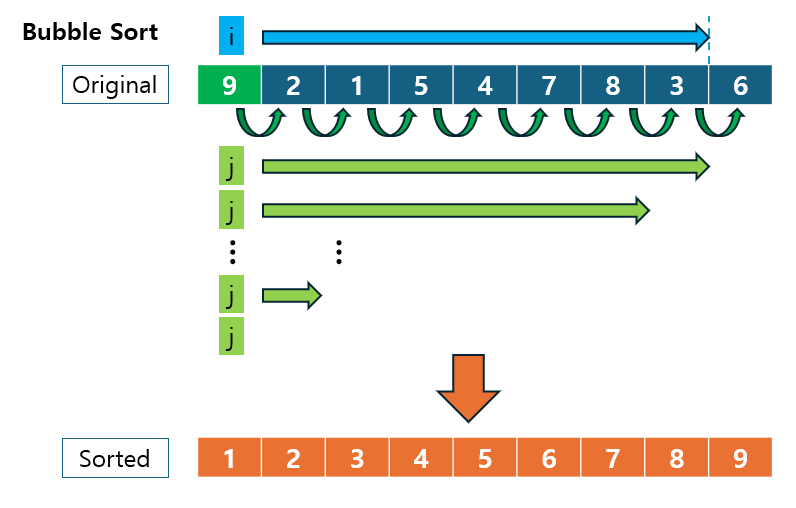
버블 정렬 (Bubble Sort)은 가장 간단한 정렬 알고리즘 중 하나로, 인접한 두 요소를 반복적으로 비교하여, 잘못된 순서의 요소들을 교환하며 정렬하는 방식입니다.

• 이 과정이 마치 "거품이 올라오는" 과정과 비슷해서 Bubble Sort라는 이름이 붙었습니다.

2.1 Bubble Sort란?

Bubble Sort는 비교 기반 정렬 알고리즘으로, 주어진 배열이나 리스트에서 인접한 두 요소를 비교하여 크기가 잘못된 경우 교환합니다.

• 이 과정을 배열의 끝까지 반복하는데, 한 번의 패스에서 가장 큰 값이 오른쪽 끝으로 이동하게 됩니다.
• 이 과정을 여러 번 반복하여 모든 요소가 정렬될 때까지 수행합니다.

• 시간 복잡도:
  • 최악 및 평균 : $O(n^2)$,
  • 최선 : $O(n)$ (이미 정렬된 경우)
• 특징:
  • 간단한 구현
  • 성능이 낮지만, 학습용으로 자주 사용됨

2.2 Bubble Sort 동작 원리

Bubble Sort는 다음과 같은 순서로 동작합니다:

1. 배열의 첫 번째 요소부터 마지막에서 두 번째 요소까지 순차적으로 인접한 요소와 비교합니다.
2. 왼쪽 요소가 오른쪽 요소보다 크면 두 요소를 교환합니다.
3. 한 번의 패스가 끝나면, 가장 큰 요소가 오른쪽 끝에 위치하게 됩니다.
4. 이 과정을 반복하면서, 비교 범위를 줄여나가며 배열을 정렬합니다.
5. 배열이 완전히 정렬될 때까지 패스를 반복합니다.

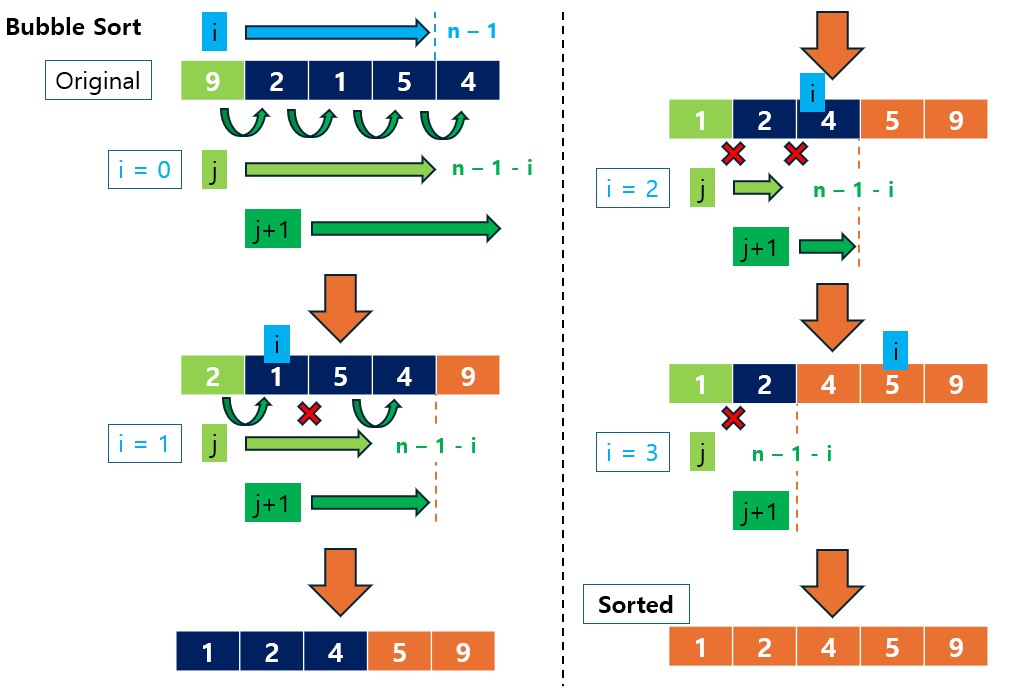
동작 예시:

주어진 배열 [9, 2, 1, 5, 4]를 Bubble Sort로 정렬하는 과정:

• 첫 번째 패스: 인접한 두 요소를 비교하며, 가장 큰 값이 배열의 끝으로 이동
  • [9, 2, 1, 5, 4] → [2, 9, 1, 5, 4] → [2, 1, 9, 5, 4] → [2, 1, 5, 9, 4] → [2, 1, 5, 4, 9]
  • 결과: 가장 큰 값인 9가 배열의 맨 끝으로 이동
• 두 번째 패스: 9는 이미 정렬되었으므로, 남은 부분을 정렬
  • [2, 1, 5, 4, 9] → [1, 2, 5, 4, 9] → [1, 2, 5, 4, 9] → [1, 2, 4, 5, 9]
  • 결과: 두 번째로 큰 값 5가 그 다음 위치로 이동
• 세 번째 패스: 더 이상 교환할 값이 없어 정렬 완료
  • [1, 2, 4, 5, 9] (정렬 완료)

2.3 Bubble Sort 구현 (Java)

import java.util.Arrays;

public class BubbleSort {
    public static void bubbleSort(int[] arr) {
        int n = arr.length;
        // 배열 전체에 대해 반복
        for (int i = 0; i < n - 1; i++) {
            // 마지막 i개의 요소는 이미 정렬되었으므로 비교할 필요 없음
            for (int j = 0; j < n - i - 1; j++) {
                // 인접한 두 요소 비교
                if (arr[j] > arr[j + 1]) {
                    // 두 요소를 교환
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = {9, 2, 1, 5, 4};
        bubbleSort(arr);
        System.out.println("Sorted array: " + Arrays.toString(arr));
    }
}

Java 구현 설명:

• 이중 for문을 사용하여 배열의 각 요소를 비교하고, 인접한 두 요소가 잘못된 순서일 경우 교환하는 방식입니다.
• 외부 루프는 배열의 패스 횟수를 제어하고, 내부 루프는 배열을 순차적으로 비교하여 정렬을 진행합니다.
• 배열이 정렬될 때까지 가장 큰 요소가 오른쪽 끝으로 이동하고, 이 과정을 반복합니다.

출력 예시:

Sorted array: [1, 2, 4, 5, 9]

2.4 Bubble Sort 구현 (Python)

def bubble_sort(arr):
    n = len(arr)
    # 배열 전체에 대해 반복
    for i in range(n-1):
        # 마지막 i개의 요소는 이미 정렬되었으므로 비교할 필요 없음
        for j in range(n-1-i):
            # 인접한 두 요소 비교
            if arr[j] > arr[j+1]:
                # 두 요소를 교환
                arr[j], arr[j+1] = arr[j+1], arr[j]

# 예시 배열
arr = [9, 2, 1, 5, 4]
bubble_sort(arr)
print("Sorted array:", arr)

Python 구현 설명:

• 파이썬의 for문과 range() 함수를 사용하여 배열의 각 요소를 반복적으로 비교합니다.
• 배열 내 요소 교환은 파이썬의 특수 문법을 사용하여 간편하게 표현(arr[j], arr[j+1] = arr[j+1], arr[j]) 가능합니다.
• 배열의 끝에서부터 가장 큰 값을 찾아가는 방식으로 정렬됩니다.

출력 예시:

Sorted array: [1, 2, 4, 5, 9]

3. Selection Sort (선택 정렬)

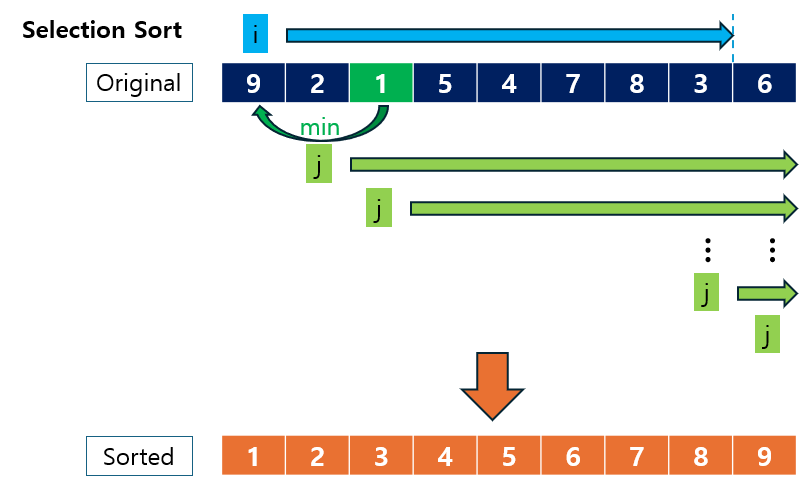
선택 정렬 (Selection Sort)은 배열에서 가장 작은(또는 가장 큰) 요소를 반복적으로 선택하여, 정렬되지 않은 부분의 맨 앞 요소와 교환하는 방식으로 정렬하는 알고리즘입니다. 이 과정이 끝날 때마다 배열의 일부가 정렬됩니다.

3.1 Selection Sort란?

Selection Sort는 비교 기반 정렬 알고리즘으로, 가장 작은 요소를 반복적으로 찾아 배열의 앞부분에 배치합니다.

• 이 방식은 배열에서 최소값을 찾아내고, 해당 값을 배열의 첫 번째 요소와 교환한 후, 나머지 부분에서 다시 최소값을 찾아 순차적으로 교환을 반복합니다.

• 시간 복잡도:
  • $O(n^2)$ (최선, 평균, 최악 모두 동일)
• 특징:
  • 비교 횟수는 많지만, 교환 횟수는 적음.
  • 작은 배열에서는 효율적일 수 있음.
  • 불안정 정렬.

3.2 Selection Sort 동작 원리

Selection Sort는 다음과 같은 순서로 동작합니다:

1. 배열에서 가장 작은 요소를 찾습니다.
2. 가장 작은 요소를 정렬되지 않은 부분의 맨 앞 요소와 교환합니다.
3. 배열의 맨 앞 요소는 정렬된 상태로 확정됩니다.
4. 나머지 배열에 대해 이 과정을 반복하여, 가장 작은 요소를 찾아 정렬합니다.
5. 배열의 끝까지 이 과정을 반복하여 배열을 정렬합니다.

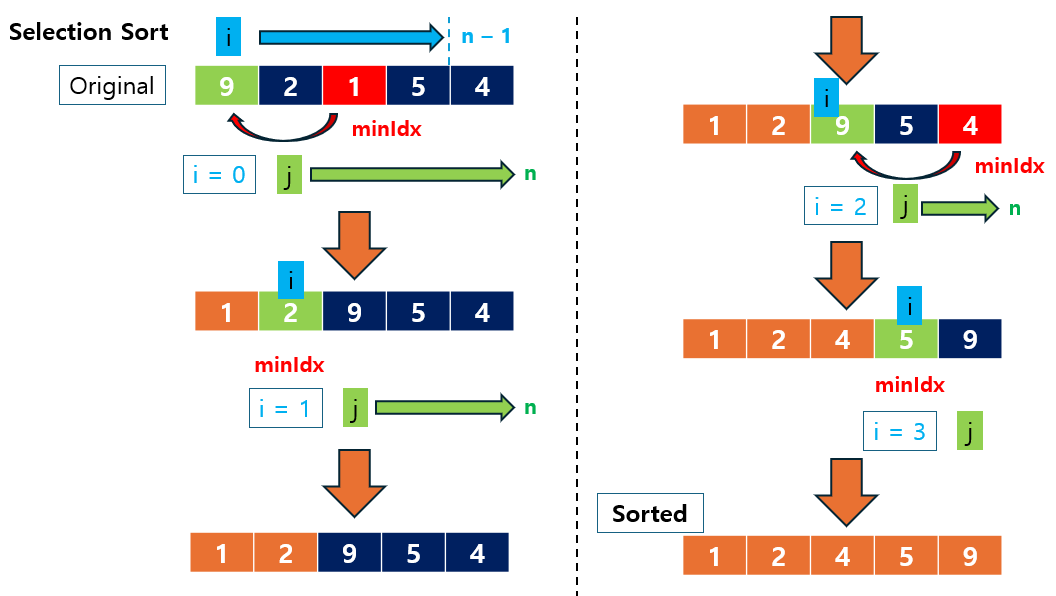
동작 예시:

주어진 배열 [9, 2, 1, 5, 4]를 Selection Sort로 정렬하는 과정:

• 첫 번째 패스: 배열에서 가장 작은 값 1을 찾아 맨 앞 요소 9와 교환
  • [9, 2, 1, 5, 4] → [1, 2, 9, 5, 4]
• 두 번째 패스: 나머지 배열 [2, 9, 5, 4]에서 가장 작은 값 2는 이미 제자리에 있음
  • [1, 2, 9, 5, 4] (변화 없음)
• 세 번째 패스: 배열 [9, 5, 4]에서 가장 작은 값 4를 찾아 9와 교환
  • [1, 2, 9, 5, 4] → [1, 2, 4, 5, 9]
• 네 번째 패스: 마지막으로 남은 배열 [5, 9]에서 정렬 완료
  • [1, 2, 4, 5, 9] (정렬 완료)

3.3 Selection Sort 구현 (Java)

import java.util.Arrays;

public class SelectionSort {
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        // 배열 전체에 대해 반복
        for (int i = 0; i < n - 1; i++) {
            // 현재 구간에서 가장 작은 요소 찾기
            int minIndex = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            // 가장 작은 요소를 현재 구간의 맨 앞 요소와 교환
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }

    public static void main(String[] args) {
        int[] arr = {9, 2, 1, 5, 4};
        selectionSort(arr);
        System.out.println("Sorted array: " + Arrays.toString(arr));
    }
}

Java 구현 설명:

• 이중 for문을 사용하여 배열에서 가장 작은 요소를 찾아 현재 구간의 맨 앞 요소와 교환합니다.
• 내부 루프에서 최소값의 인덱스를 찾아 교환 작업을 수행합니다.
• 배열의 끝까지 이 과정을 반복하면서 정렬이 완료됩니다.

출력 예시:

Sorted array: [1, 2, 4, 5, 9]

3.4 Selection Sort 구현 (Python)

def selection_sort(arr):
    n = len(arr)
    # 배열 전체에 대해 반복
    for i in range(n-1):
        # 현재 구간에서 가장 작은 요소 찾기
        min_index = i
        for j in range(i+1, n):
            if arr[j] < arr[min_index]:
                min_index = j
        # 가장 작은 요소를 현재 구간의 맨 앞 요소와 교환
        arr[i], arr[min_index] = arr[min_index], arr[i]

# 예시 배열
arr = [9, 2, 1, 5, 4]
selection_sort(arr)
print("Sorted array:", arr)

Python 구현 설명:

• 파이썬의 for문을 사용하여 배열에서 최소값을 찾아 현재 구간의 첫 번째 요소와 교환합니다.
• 배열 내 요소 교환은 파이썬의 특수 문법을 사용하여 간단하게 처리(arr[i], arr[min_index] = arr[min_index], arr[i])합니다.
• 배열이 끝날 때까지 최소값을 찾아가며 배열이 정렬됩니다.

출력 예시:

Sorted array: [1, 2, 4, 5, 9]

4. 단순 정렬 알고리즘 비교

단순 정렬 알고리즘들은 구현이 쉽고 이해하기 간단하지만, 대규모 데이터에서는 비효율적일 수 있습니다.

• 버블 정렬과 선택 정렬은 모두 평균적으로 $O(n^2)$의 시간 복잡도를 가지고 있습니다.

알고리즘	시간 복잡도 (최악, 평균)	공간 복잡도	특징
Bubble Sort	$O(n^2)$	$O(1)$	구현이 간단하지만 비교 및 교환이 빈번하게 발생
Selection Sort	$O(n^2)$	$O(1)$	교환 횟수는 적지만, 비교 횟수는 많음
Insertion Sort	$O(n^2)$ (최선 $O(n)$)	$O(1)$	작은 배열이나 이미 정렬된 배열에서 효율적

• 버블 정렬은 인접한 요소를 교환하며 배열을 정렬하는 방식으로, 비교적 느리지만 단순한 구조로 학습 목적에 적합합니다.
• 반면, 선택 정렬은 비교 횟수는 많지만 교환 횟수가 적어, 교환 비용이 큰 경우 적합할 수 있습니다.

이들 알고리즘은 모두 작은 배열에서의 사용에 적합하며, 대규모 데이터에서는 보다 효율적인 정렬 알고리즘을 사용하는 것이 바람직합니다.

마무리

이번 포스팅에서는 대표적인 단순 정렬 알고리즘인 버블 정렬과 선택 정렬을 다루었습니다.

• 두 정렬 모두 시간 복잡도 면에서는 비효율적일 수 있지만, 구현이 간단하고 교육 목적으로 많이 활용되는 알고리즘입니다.
• 단순 정렬 알고리즘은 작은 데이터셋에서는 여전히 유용하며, 각각의 알고리즘이 어떻게 동작하는지 이해하는 것은 복잡한 정렬 알고리즘을 배우는 데 중요한 토대가 됩니다.

다음 포스팅에서는 단순 정렬 알고리즘 중에서 가장 활용도가 높은 삽입 정렬과 이진 삽입 정렬에 대해 다룰 예정입니다.