본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

• 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
  • IDE : IntelliJ IDEA (Ultimate Edition)
  • Java : JDK 21 (corretto-21)
  • Python : 3.9 (conda env)

[알고리즘] 분할 정복(Divide and Conquer)

1. Divide and Conquer란?

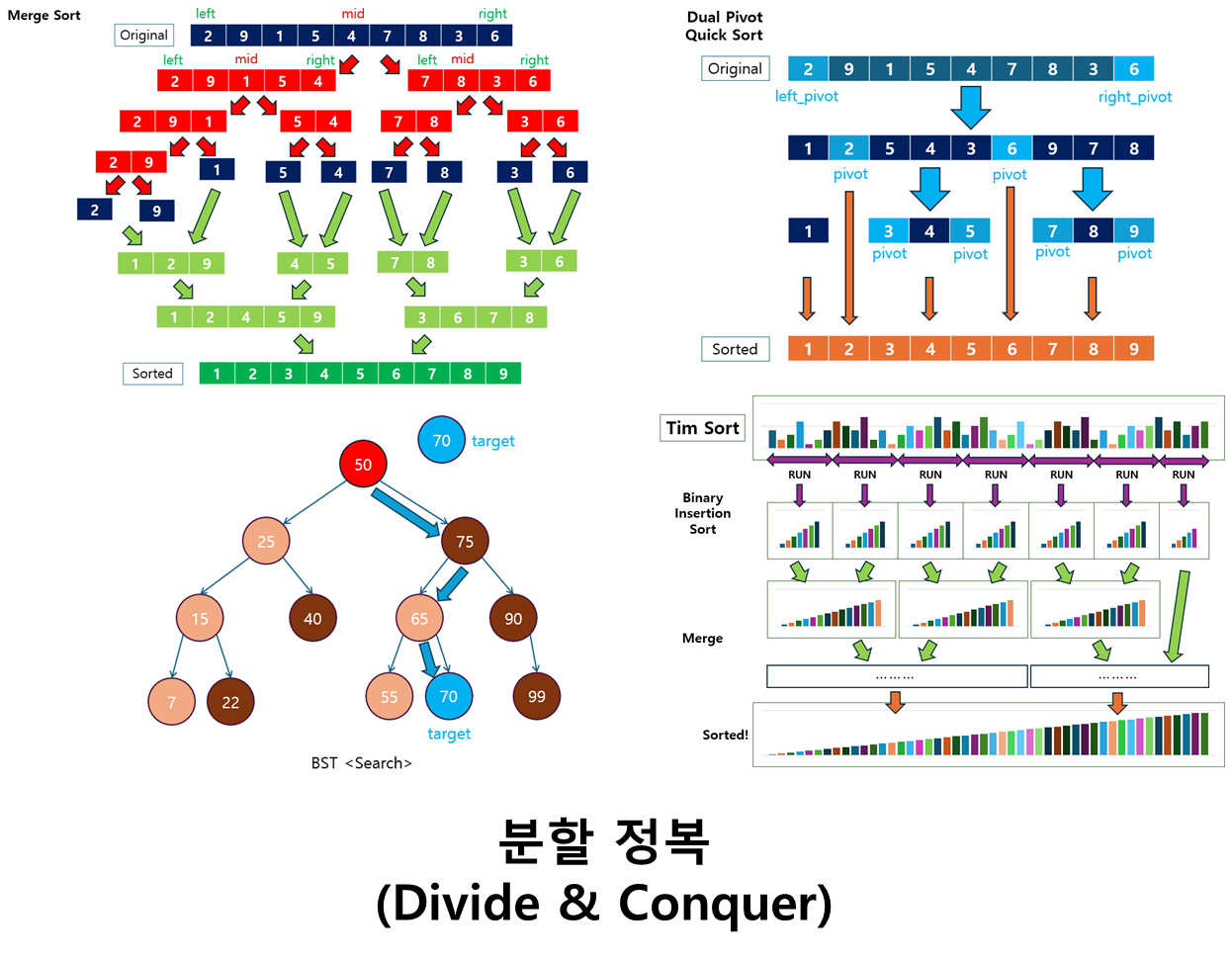
분할 정복(Divide and Conquer)는 문제를 작은 단위로 나누어 해결하는 방식으로, 특히 복잡한 문제를 간단한 문제들로 나누어 처리하고, 그 결과를 결합하여 최종 해결책을 구하는 알고리즘 설계 기법입니다.

• 이 기법은 재귀적으로 문제를 해결하는 과정에서 주로 사용되며, 다양한 알고리즘에서 핵심적으로 활용됩니다.

분할 정복 기법의 과정은 세 단계로 요약할 수 있습니다:

1. 분할(Divide): 주어진 문제를 해결하기 쉬운 작은 문제들로 재귀적으로 나누는 단계입니다. 문제의 크기가 줄어들면서 다루기 쉬워지거나 기저 사례(base case)에 도달하게 됩니다.

2. 정복(Conquer): 나누어진 작은 문제들을 개별적으로 해결합니다. 작은 문제들은 종종 재귀적으로 처리되며, 문제의 크기가 충분히 작아지면 더 이상 나눌 필요 없이 해결됩니다.

3. 결합(Combine): 해결된 작은 문제들을 다시 결합하여 원래 문제의 최종 해답을 얻습니다. 이 과정에서 병합이나 조합이 이루어지며, 문제가 분할되었던 방식에 따라 결합 방식도 달라집니다.

1.1 분할 정복의 대표적인 알고리즘

• Merge Sort (합병 정렬):

  • 주어진 배열을 반으로 나누고, 각각의 부분 배열을 재귀적으로 정렬한 뒤, 정렬된 부분 배열들을 병합하여 최종 정렬을 완료하는 방식입니다.
  • 시간 복잡도는 O(n log n)이며, 항상 안정적인 성능을 보장합니다.

• Quick Sort (퀵 정렬):

  • 주어진 배열에서 피벗 값을 설정하고, 피벗을 기준으로 작은 값과 큰 값으로 배열을 분할한 뒤, 각각의 부분 배열을 재귀적으로 정렬하는 방식입니다.
  • 평균 시간 복잡도는 O(n log n)이지만, 최악의 경우 O(n²)가 될 수 있습니다.

• Binary Search (이진 탐색):

  • 정렬된 배열에서 원하는 값을 찾기 위해 배열을 중간 값으로 나누어, 중간 값과의 비교를 통해 탐색 범위를 절반으로 줄이는 방식입니다.
  • 이진 탐색의 시간 복잡도는 O(log n)입니다.

• Closest Pair of Points (최근접 두 점 문제):

  • 평면 상의 여러 점들 중에서 두 점 사이의 거리가 가장 짧은 두 점을 찾는 문제입니다.
  • 분할 정복을 이용해 점들을 나누고, 각각의 작은 문제를 해결한 뒤, 결과를 결합하여 전체 문제를 해결하는 방식으로 접근합니다.

1.2 분할 정복 기법의 장단점

분할 정복 기법의 장점:

• 시간 복잡도 개선:
  • 많은 문제에서 시간 복잡도를 선형 로그 시간 또는 로그 시간으로 줄일 수 있습니다. 이는 문제를 효율적으로 나누고 결합하는 과정에서 얻는 이점입니다.
• 재귀적 문제 해결:
  • 문제를 작은 부분으로 나누는 과정에서, 같은 형태의 작은 문제를 반복적으로 해결할 수 있으므로, 재귀적 구조에 적합합니다.
• 다양한 문제 적용 가능:
  • 정렬, 탐색, 최적화 문제 등 다양한 알고리즘 문제에서 효과적으로 사용될 수 있습니다.

분할 정복 기법의 단점:

• 재귀 호출의 오버헤드:
  • 분할하는 과정에서 많은 재귀 호출이 발생하여, 스택 오버플로우(stack overflow)의 위험이 있습니다.
  • 특히 매우 큰 문제에서는 이를 피하기 위한 추가적인 최적화가 필요합니다.
• 추가 메모리 사용:
  • 문제를 분할하고 해결하는 과정에서, 때로는 추가적인 메모리 공간이 필요할 수 있습니다.
  • 예를 들어, 합병 정렬에서는 추가 배열을 사용하여 병합을 처리합니다.

2. Divide and Conquer의 주요 알고리즘

분할 정복(Divide and Conquer)은 다양한 알고리즘에서 핵심 기법으로 사용됩니다.

• 이 섹션에서는 대표적인 분할 정복 기반 알고리즘을 다루고, 각 알고리즘의 동작 원리와 구현 방식에 대해 설명하겠습니다.

2.1 Merge Sort (합병 정렬)

Merge Sort는 배열을 분할하여 재귀적으로 정렬하고, 다시 병합하여 최종 정렬된 배열을 만드는 대표적인 분할 정복 알고리즘입니다.

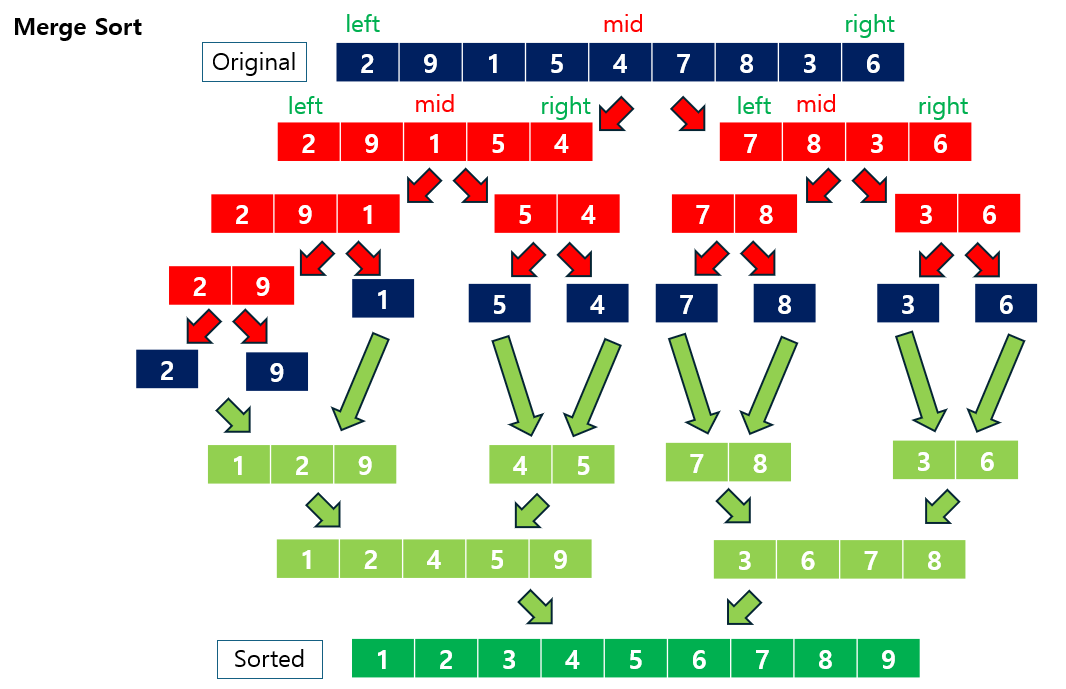
동작 원리:

1. 분할: 배열을 절반으로 나누어 두 개의 하위 배열로 분할합니다.
2. 정복: 각각의 하위 배열을 재귀적으로 Merge Sort를 사용하여 정렬합니다.
3. 병합: 정렬된 하위 배열을 병합하여 하나의 배열로 만듭니다.

시간 복잡도:

• O(n log n): 배열을 분할하는 단계에서 log n이 소요되고, 병합하는 과정에서 O(n) 시간이 걸리므로 전체 복잡도는 O(n log n)입니다.

// Java로 구현된 Merge Sort 예시
public class MergeSort {
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int middle = (left + right) / 2;
            mergeSort(arr, left, middle);
            mergeSort(arr, middle + 1, right);
            merge(arr, left, middle, right);
        }
    }

    public static void merge(int[] arr, int left, int middle, int right) {
        int n1 = middle - left + 1;
        int n2 = right - middle;
        int[] leftArr = new int[n1];
        int[] rightArr = new int[n2];
        for (int i = 0; i < n1; i++) leftArr[i] = arr[left + i];
        for (int j = 0; j < n2; j++) rightArr[j] = arr[middle + 1 + j];
        int i = 0, j = 0, k = left;
        while (i < n1 && j < n2) {
            if (leftArr[i] <= rightArr[j]) arr[k++] = leftArr[i++];
            else arr[k++] = rightArr[j++];
        }
        while (i < n1) arr[k++] = leftArr[i++];
        while (j < n2) arr[k++] = rightArr[j++];
    }

    public static void main(String[] args) {
        int[] arr = {9, 2, 5, 1, 7};
        mergeSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }
}

2.2 Quick Sort (퀵 정렬)

Quick Sort는 피벗(Pivot)을 선택한 후 피벗보다 작은 값과 큰 값을 각각 좌우로 분할하여 재귀적으로 정렬하는 알고리즘입니다.

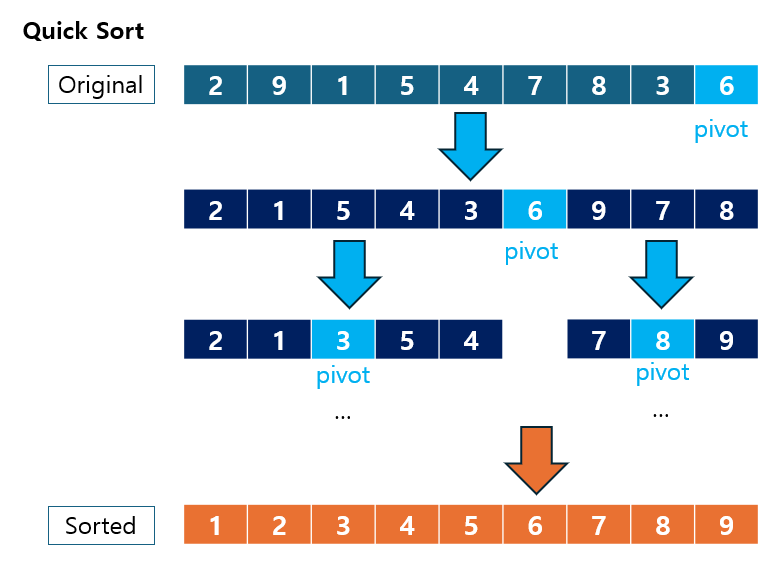
동작 원리:

1. 분할: 배열에서 피벗을 선택하고, 피벗보다 작은 값과 큰 값을 기준으로 두 개의 하위 배열로 나눕니다.
2. 정복: 각 하위 배열을 재귀적으로 정렬합니다.
3. 결합: 분할된 배열을 합치진 않고, 이미 정렬된 상태로 유지됩니다.

시간 복잡도:

• 평균: O(n log n)
• 최악: O(n²) (피벗이 최적이 아닐 경우)

# Python으로 구현된 Quick Sort 예시
def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

arr = [10, 5, 2, 3, 7]
sorted_arr = quick_sort(arr)
print(sorted_arr)

2.3 Binary Search (이진 탐색)

Binary Search는 정렬된 배열에서 특정 값을 빠르게 찾는 알고리즘으로, 분할 정복을 활용하여 배열을 절반씩 나누면서 탐색 범위를 줄여갑니다.

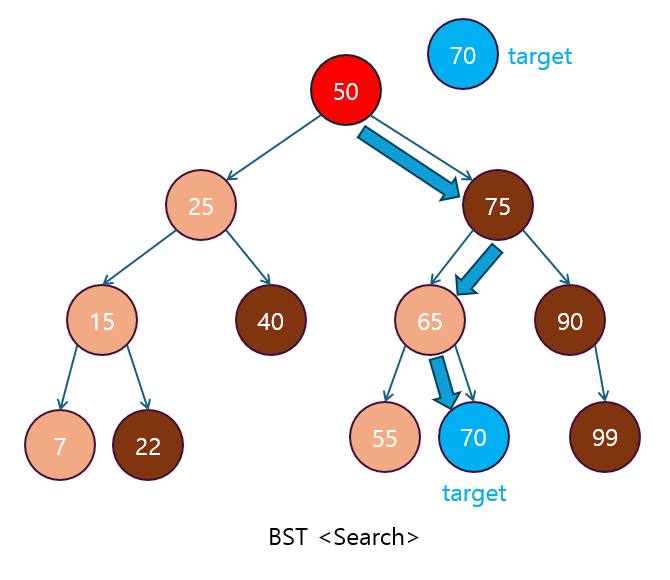
동작 원리:

1. 분할: 배열의 중간 값을 기준으로 탐색할 값이 중간 값보다 크거나 작은지에 따라 좌우로 나눕니다.
2. 정복: 탐색 범위를 절반으로 줄이고, 재귀적으로 탐색합니다.
3. 결합: 탐색한 값을 결합할 필요 없이 바로 반환합니다.

시간 복잡도: O(log n)

// Java로 구현된 Binary Search 예시
public class BinarySearch {
    public static int binarySearch(int[] arr, int target, int left, int right) {
        if (left > right) return -1;
        int mid = (left + right) / 2;
        if (arr[mid] == target) return mid;
        else if (arr[mid] > target) return binarySearch(arr, target, left, mid - 1);
        else return binarySearch(arr, target, mid + 1, right);
    }

    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, 9};
        int target = 5;
        int index = binarySearch(arr, target, 0, arr.length - 1);
        System.out.println("Index of target: " + index);
    }
}

3. Divide and Conquer의 알고리즘 복잡도

분할 정복 기법을 사용한 알고리즘들은 시간 복잡도와 공간 복잡도 측면에서 효율적인 성능을 보입니다.

• 하지만 각 알고리즘의 특성과 문제의 성격에 따라 성능이 달라지기 때문에, 이를 종합적으로 이해하는 것이 중요합니다.
• 이 섹션에서는 대표적인 분할 정복 기반 알고리즘들의 복잡도를 분석해보겠습니다.

3.1 Merge Sort의 복잡도

시간 복잡도:

• 최선, 평균, 최악: $O(n \log n)$
• Merge Sort는 항상 일정하게 O(n log n)의 시간 복잡도를 유지합니다.
  • 배열을 계속해서 절반으로 나누며 log n의 분할 과정을 거치고, 각 분할된 부분을 병합하는데 O(n)의 시간이 걸리기 때문에 전체 복잡도는 O(n log n)입니다.

공간 복잡도:

• O(n): Merge Sort는 추가적인 메모리 공간이 필요합니다.
  • 특히, 병합 과정에서 추가 배열을 사용하여 원래 배열의 부분 배열을 저장하고 병합하기 때문에 O(n)의 추가 공간이 필요합니다.

특징:

• Merge Sort는 안정적인 정렬 알고리즘으로, 같은 값을 가진 요소들의 상대적인 순서가 유지됩니다.
• 또한, 최악의 경우에도 O(n log n)을 보장하므로, 일관된 성능을 보입니다.

3.2 Quick Sort의 복잡도

시간 복잡도:

• 평균: $O(n \log n)$
• 최악: $O(n^2)$
• Quick Sort는 평균적으로 O(n log n)의 성능을 보이지만, 피벗 선택이 비효율적일 경우(매번 가장 작은 값 또는 큰 값이 피벗으로 선택되는 경우) $O(n^2)$로 성능이 저하될 수 있습니다.
  • 그러나 최적화된 피벗 선택 기법을 사용하면 이를 방지할 수 있습니다.

공간 복잡도:

• O(log n) (평균): Quick Sort는 재귀 호출에 의해 스택 공간이 사용됩니다.
  • 일반적으로, 분할이 균형 있게 이루어지면 재귀 깊이는 log n이므로 공간 복잡도는 O(log n)이 됩니다.
• O(n) (최악): 피벗이 비효율적으로 선택되어 불균형하게 분할되면 스택 오버플로우가 발생할 수 있으며, 이 경우 공간 복잡도는 최악의 경우 O(n)이 될 수 있습니다.

특징:

• Quick Sort는 제자리 정렬(in-place sorting) 알고리즘으로, 추가적인 메모리 공간을 최소화합니다. 그러나 피벗 선택에 따라 성능이 크게 달라질 수 있습니다.

3.3 Binary Search의 복잡도

시간 복잡도:

• O(log n): 이진 탐색은 배열을 반으로 나누며 탐색을 진행하기 때문에, 시간 복잡도는 항상 O(log n)입니다. 따라서 큰 데이터셋에서 매우 효율적입니다.

공간 복잡도:

• O(1) (비재귀적): 이진 탐색의 비재귀적 구현은 추가적인 메모리 공간을 거의 사용하지 않으므로 공간 복잡도는 O(1)입니다.
• O(log n) (재귀적): 재귀적으로 구현할 경우, 재귀 호출 스택이 사용되므로 공간 복잡도는 O(log n)이 됩니다.

특징:

• Binary Search는 정렬된 배열에서만 사용할 수 있으며, 정렬이 선행된 데이터셋에서 매우 빠르게 작동합니다.
  • O(log n)의 시간 복잡도를 가지므로, 탐색 효율이 매우 높은 편입니다.

3.4 종합 비교

알고리즘	시간 복잡도 (평균)	시간 복잡도 (최악)	공간 복잡도	특징
Merge Sort	O(n log n)	O(n log n)	O(n)	항상 일정한 성능 보장, 안정 정렬
Quick Sort	O(n log n)	O(n²)	O(log n)	제자리 정렬, 피벗 선택에 따라 성능 변동
Binary Search	O(log n)	O(log n)	O(1)	정렬된 배열에서만 사용, 빠른 탐색

이 표에서 볼 수 있듯이, 각 알고리즘은 문제의 성격에 따라 다르게 사용됩니다.

• Merge Sort는 항상 O(n log n)의 성능을 보장하지만, 추가적인 메모리가 필요합니다.
• 반면 Quick Sort는 메모리 사용이 적지만, 피벗 선택에 따라 성능이 달라질 수 있습니다.
• Binary Search는 탐색 문제에서 매우 유용하지만, 정렬된 배열에서만 사용할 수 있다는 제약이 있습니다.

마무리

이번 포스팅에서는 분할 정복(Divide and Conquer) 알고리즘의 개념과 주요 알고리즘들을 살펴보았습니다.

• 분할 정복은 문제를 작은 단위로 나누고, 그 문제들을 해결한 후 결합하는 방식으로 복잡한 문제를 해결하는 강력한 기법입니다.

특히 Merge Sort, Quick Sort, Binary Search와 같은 대표적인 알고리즘들이 어떻게 분할 정복 기법을 활용하여 효율적으로 동작하는지, 그 원리와 복잡도를 살펴보았습니다.

• 각 알고리즘은 상황에 따라 적합한 경우가 있으며, 데이터의 특성이나 메모리 제약에 따라 올바른 알고리즘을 선택하는 것이 중요합니다.

분할 정복은 정렬과 탐색뿐만 아니라 최적화 문제, 그래프 문제 등 다양한 문제에서도 응용될 수 있는 강력한 도구입니다.

앞으로의 포스팅에서는 탐색 알고리즘, 최적화 알고리즘 등 다른 다양한 문제 해결 기법들을 다루어볼 예정입니다.