[알고리즘] 탐색(Search) - Two-Pointer & Binary Search [개념과 활용]

Kyung Jae, Cheong·2024년 10월 24일
Javapython알고리즘
0

알고리즘-Algorithms

목록 보기
9/15
post-thumbnail

본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

  • 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
    • IDE : IntelliJ IDEA (Ultimate Edition)
    • Java : JDK 21 (corretto-21)
    • Python : 3.9 (conda env)

탐색(Search) - Two-Pointer & Binary Search

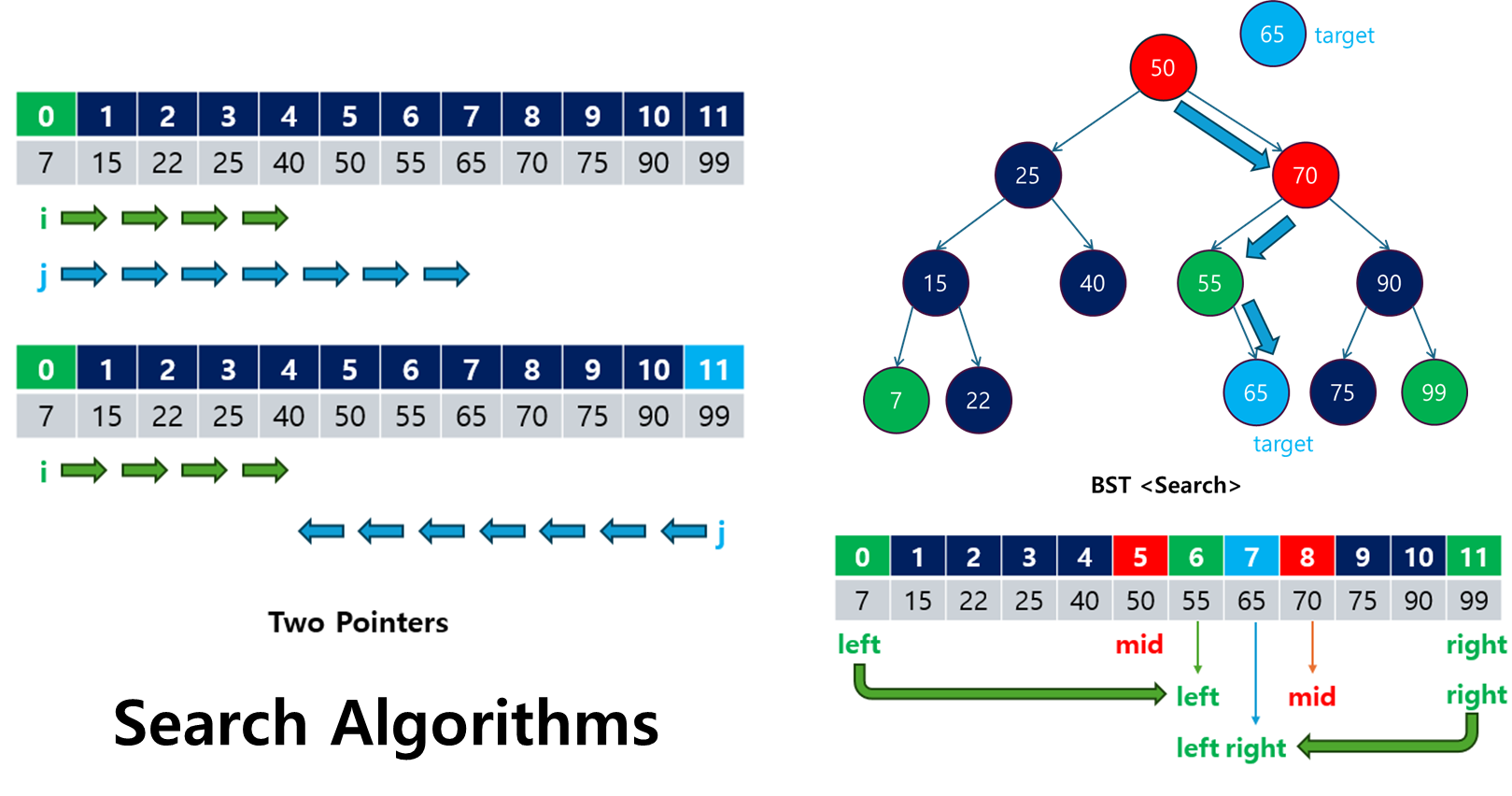
1. 탐색(Search) 알고리즘이란?

탐색(Search) 알고리즘은 주어진 데이터 구조 내에서 원하는 데이터를 찾아내기 위한 일련의 과정입니다.

  • 배열, 트리, 그래프와 같은 자료구조에서 특정 값을 찾거나, 문제에서 요구하는 조건에 맞는 해답을 도출할 때 사용됩니다.
  • 효율적인 탐색 알고리즘을 활용하면 시간과 자원을 절약할 수 있으며, 특히 데이터의 규모가 커질수록 그 중요성이 커집니다.

탐색 알고리즘은 크게 두 가지 범주로 나눌 수 있습니다:

  1. 배열 기반 탐색
    배열을 기반으로 원하는 값을 찾거나 조건을 만족하는 요소를 탐색하는 알고리즘입니다.
  • 선형 탐색(Linear Search): 배열을 처음부터 끝까지 하나씩 살펴보며 찾는 방식. 가장 기본적인 탐색 방법이지만, 속도가 느립니다.
  • 이진 탐색(Binary Search): 정렬된 배열에서 중간 값을 기준으로 탐색 범위를 절반으로 좁혀가며 찾는 방식. 시간 복잡도가 O(log n)으로 매우 효율적입니다.
  • 투 포인터(Two-Pointer): 배열의 양쪽 끝에서 시작해 조건을 만족할 때까지 포인터를 조정하는 방식. 주로 정렬된 배열에서 두 수의 합 등을 찾는 문제에 사용됩니다.
  1. 그래프 및 트리 기반 탐색
    트리나 그래프와 같은 비선형 자료구조에서 특정 값을 찾는 알고리즘입니다.
  • 깊이 우선 탐색(DFS): 한 경로를 끝까지 탐색한 후, 다른 경로로 백트래킹하며 탐색하는 방식. 순환 구조나 경로 찾기 문제에 유용합니다.
  • 너비 우선 탐색(BFS): 시작 지점에서 가까운 노드를 먼저 탐색하며 점진적으로 넓혀가는 방식. 최단 경로 탐색 문제에 적합합니다.
  • 백트래킹(Backtracking): 가능한 모든 경로를 탐색하되, 유망하지 않은 경로는 중간에 포기하는 방식. 그래프나 트리뿐만 아니라 배열에서 순열, 조합, 부분집합을 찾는 문제에도 자주 사용됩니다.

이번 시리즈에서는 이러한 다양한 탐색 알고리즘을 순차적으로 다루면서 그 개념과 활용 방법을 소개합니다.
이번 포스팅에서는 배열 기반의 투 포인터(Two-Pointer)와 이진 탐색(Binary Search)을 중점적으로 설명하고, 이후 포스팅에서는 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS), 백트래킹(Backtracking) 등의 보다 복잡한 탐색 기법들을 다룰 예정입니다.

2. Two-Pointer 알고리즘

Two-Pointer 알고리즘은 배열과 같은 선형 자료구조에서 두 개의 포인터를 이용해 원하는 조건을 만족하는 값을 찾는 알고리즘입니다.

  • 주로 정렬된 배열에서 사용되며, 이 알고리즘의 장점은 배열을 처음부터 끝까지 탐색하지 않고도 효율적으로 값을 찾을 수 있다는 점입니다.

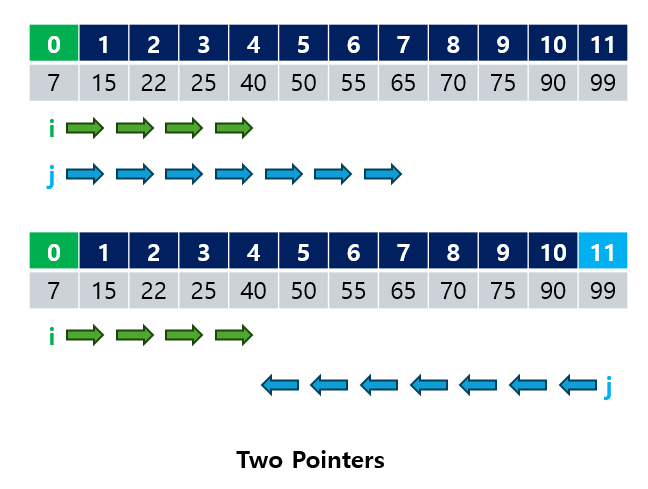
2.1 Two-Pointer 알고리즘의 동작 원리

Two-Pointer 알고리즘은 두 포인터를 배열의 서로 다른 위치에 두고 점차적으로 이동시키며 탐색하는 방식입니다. 포인터가 시작되는 위치에 따라 두 가지 일반적인 경우가 있습니다.

2.1.1 양 끝에서 시작하는 경우

두 포인터를 배열의 양쪽 끝에 두고, 각각 서로를 향해 이동시키는 방식입니다.

  • 왼쪽 포인터(i): 배열의 시작 위치에서 출발해 오른쪽으로 이동합니다.
  • 오른쪽 포인터(j): 배열의 끝 위치에서 출발해 왼쪽으로 이동합니다.

이 방식은 주로 두 수의 합을 찾는 문제에서 사용됩니다.

  • 예를 들어, 특정 합을 만들기 위한 두 요소를 찾을 때, 두 포인터를 이용해 탐색 범위를 좁혀가며 빠르게 결과를 도출할 수 있습니다.

2.1.2 같은 방향에서 시작하는 경우

두 포인터가 같은 방향에서 출발해 한쪽으로 이동하는 방식입니다.

  • 두 포인터 모두 왼쪽에서 시작해 오른쪽으로 이동하거나,
  • 오른쪽에서 시작해 왼쪽으로 이동할 수 있습니다.

이 방식은 주로 부분합이나 연속된 구간을 찾는 문제에서 사용됩니다.

  • 예를 들어, 연속된 부분 배열의 합이 특정 값을 만족하는지 확인할 때, 두 포인터를 이용해 구간을 확장하거나 축소하며 문제를 해결할 수 있습니다.

2.2 Two-Pointer 알고리즘 예시

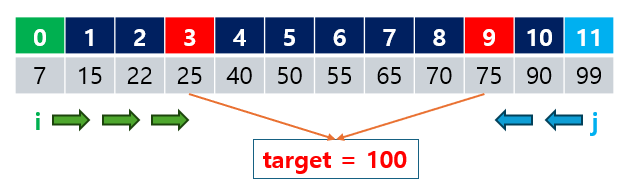
예시 1: 두 수의 합 찾기 (양 끝에서 시작)
주어진 배열 [7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99]에서 두 수의 합이 100이 되는 쌍을 찾아보겠습니다.

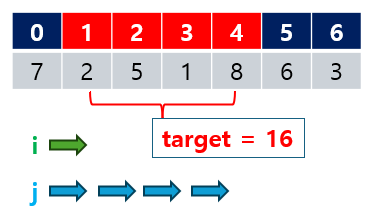
예시 2: 연속 부분 배열의 합 찾기 (같은 방향에서 시작)
정렬되지 않은 배열에서 연속된 부분 배열의 합이 특정 값을 만족하는 구간을 찾아보겠습니다.

  • 예를 들어, 배열 [7, 2, 5, 1, 8, 6, 3]에서 연속 부분 배열의 합이 16이 되는 구간을 찾는 문제입니다.

Python 코드 예시

# 예시 1: 두 수의 합 찾기 (양 끝에서 시작)
def two_sum(arr, target):
    i, j = 0, len(arr) - 1
    while i < j:
        total = arr[i] + arr[j]
        if total == target:
            return i, j
        elif total < target:
            i += 1
        else:
            j -= 1
    return None

# 예시 2: 연속 부분 배열의 합 찾기 (같은 방향에서 시작)
def find_subarray_with_sum(arr, target):
    i, j = 0, 0
    current_sum = 0
    while j < len(arr):
        current_sum += arr[j]
        while current_sum > target and i < j:
            current_sum -= arr[i]
            i += 1
        if current_sum == target:
            return i, j
        j += 1
    return None

# 테스트
arr1 = [7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99]
target1 = 100
print(two_sum(arr1, target1))  # 출력: (3, 9)

arr2 = [7, 2, 5, 1, 8, 6, 3]
target2 = 16
print(find_subarray_with_sum(arr2, target2))  # 출력: (1, 4)

Python 테스트 결과 해석

  1. 예시 1: 두 수의 합 찾기
    배열 [7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99]에서 두 수의 합이 100이 되는 값을 찾으면, 포인터가 가리키는 값 arr[3] = 25와 arr[9] = 75를 더하면 100이 됩니다.

    • 출력 결과는 (3, 9)로, 인덱스 3과 9의 값을 더한 합이 목표 값 100과 일치함을 확인할 수 있습니다.

  2. 예시 2: 연속 부분 배열의 합 찾기
    배열 [7, 2, 5, 1, 8, 6, 3]에서 연속된 부분 배열의 합이 16이 되는 구간을 찾으면, 인덱스 1에서 4까지의 구간 [2, 5, 1, 8]의 합이 16이 됩니다.

    • 출력 결과는 (1, 4)로, 연속된 부분 배열의 인덱스 1부터 4까지의 합이 16이 되는 구간을 찾았음을 확인할 수 있습니다.

Java 코드 예시

// 예시 1: 두 수의 합 찾기 (양 끝에서 시작)
public class TwoPointerExample {
    public static int[] twoSum(int[] arr, int target) {
        int i = 0, j = arr.length - 1;
        while (i < j) {
            int sum = arr[i] + arr[j];
            if (sum == target) {
                return new int[]{i, j};
            } else if (sum < target) {
                i++;
            } else {
                j--;
            }
        }
        return null;  // 합을 찾지 못한 경우
    }

    // 예시 2: 연속 부분 배열의 합 찾기 (같은 방향에서 시작)
    public static int[] findSubarrayWithSum(int[] arr, int target) {
        int i = 0, currentSum = 0;
        for (int j = 0; j < arr.length; j++) {
            currentSum += arr[j];
            while (currentSum > target && i < j) {
                currentSum -= arr[i];
                i++;
            }
            if (currentSum == target) {
                return new int[]{i, j};
            }
        }
        return null;  // 합을 찾지 못한 경우
    }

    public static void main(String[] args) {
        // 예시 1 테스트
        int[] arr1 = {7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99};
        int target1 = 100;
        int[] result1 = twoSum(arr1, target1);
        if (result1 != null) {
            System.out.println("Indices: " + result1[0] + ", " + result1[1]);
        } else {
            System.out.println("No pair found.");
        }

        // 예시 2 테스트
        int[] arr2 = {7, 2, 5, 1, 8, 6, 3};
        int target2 = 16;
        int[] result2 = findSubarrayWithSum(arr2, target2);
        if (result2 != null) {
            System.out.println("Subarray found from index " + result2[0] + " to " + result2[1]);
        } else {
            System.out.println("No subarray found.");
        }
    }
}

Java 테스트 결과 해석

  1. 예시 1: 두 수의 합 찾기
    배열 [7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99]에서 두 수의 합이 100이 되는 쌍을 찾으면, 인덱스 3의 값 25와 인덱스 9의 값 75를 더한 값이 100입니다.

    • 출력 결과는 Indices: 3, 9로, 인덱스 3과 9의 두 수가 합이 100이 되는 쌍임을 확인할 수 있습니다.

  2. 예시 2: 연속 부분 배열의 합 찾기
    배열 [7, 2, 5, 1, 8, 6, 3]에서 연속된 부분 배열의 합이 16이 되는 구간을 찾으면, 인덱스 1부터 4까지의 구간 [2, 5, 1, 8]의 합이 16입니다.

    • 출력 결과는 Subarray found from index 1 to 4로, 인덱스 1에서 4까지의 연속 부분 배열의 합이 16임을 확인할 수 있습니다.

2.3 Two-Pointer 알고리즘의 시간 복잡도

Two-Pointer 알고리즘의 시간 복잡도는 O(n)으로, 배열을 한 번만 순회하기 때문에 매우 효율적입니다.

  • 두 포인터가 배열의 양 끝에서 출발해 중앙으로 만나거나, 같은 방향으로 이동하면서 탐색을 마치기 때문에, 선형 탐색보다 빠르고 효율적인 해결책을 제공합니다.

이를 선형 탐색(Brute Force)와 비교하면, 선형 탐색의 경우는 모든 가능한 쌍을 검사해야 하므로 O(n2)O(n^2)의 시간 복잡도를 가집니다.

  • 예를 들어, 두 수의 합을 찾는 문제에서 선형 탐색은 각 요소에 대해 나머지 요소들을 모두 검사하는 방식이므로, n개의 요소에 대해 각각 n번씩 검사가 이루어집니다.

반면, Two-Pointer 알고리즘은 배열이 정렬된 상태에서 포인터를 조정해가며 필요한 계산을 하므로 한 번의 순회(O(n))만으로 문제를 해결할 수 있습니다.

  • 이러한 차이로 인해 Two-Pointer 알고리즘은 대규모 배열을 다룰 때 훨씬 더 효율적입니다.

3. Binary Serach 알고리즘

Binary Search(이진 탐색) 알고리즘은 정렬된 배열에서 특정 값을 찾기 위해 사용되는 효율적인 탐색 알고리즘입니다.

  • 이진 탐색은 배열을 절반으로 나누어 탐색 범위를 좁혀나가는 방식으로, 시간 복잡도가 O(log n)으로 매우 빠릅니다.

3.1 Binary Search 알고리즘의 동작 원리

Binary Search는 다음과 같은 단계로 동작합니다:

  1. 초기화:
    • 탐색 범위의 시작점(left)과 끝점(right)을 설정합니다.
    • 처음에는 배열의 첫 번째 요소가 시작점, 마지막 요소가 끝점으로 설정됩니다.
  2. 중간값 계산:
    • 시작점과 끝점의 중간값(mid)을 계산합니다.
    • 중간값은 (left + right) // 2로 계산됩니다.
      • 참고로 Java에서는 (left + right)에서 int 데이터 타입의 overflow가 일어날수 있습니다. 이때는 left + (right - left) // 2와 같은 방식으로 사용하시면 됩니다.
        (Python은 무한 정수를 표현 가능하므로 해당되지 않습니다)
  3. 조건 비교:
    • 중간값이 찾고자 하는 목표값(target)과 같으면 탐색이 종료됩니다.
    • 중간값이 목표값보다 크면, 탐색 범위를 중간값 왼쪽으로 좁힙니다.
      즉, right = mid - 1로 갱신합니다.
    • 중간값이 목표값보다 작으면, 탐색 범위를 중간값 오른쪽으로 좁힙니다.
      즉, left = mid + 1로 갱신합니다.
  4. 반복: 목표값을 찾거나 탐색 범위가 없을 때까지 2~3단계를 반복합니다.

이진 탐색은 배열이 정렬된 상태일 때만 사용할 수 있으며, 배열의 크기가 클수록 탐색 속도가 매우 빠릅니다.

3.2 Binary Search 알고리즘 예시

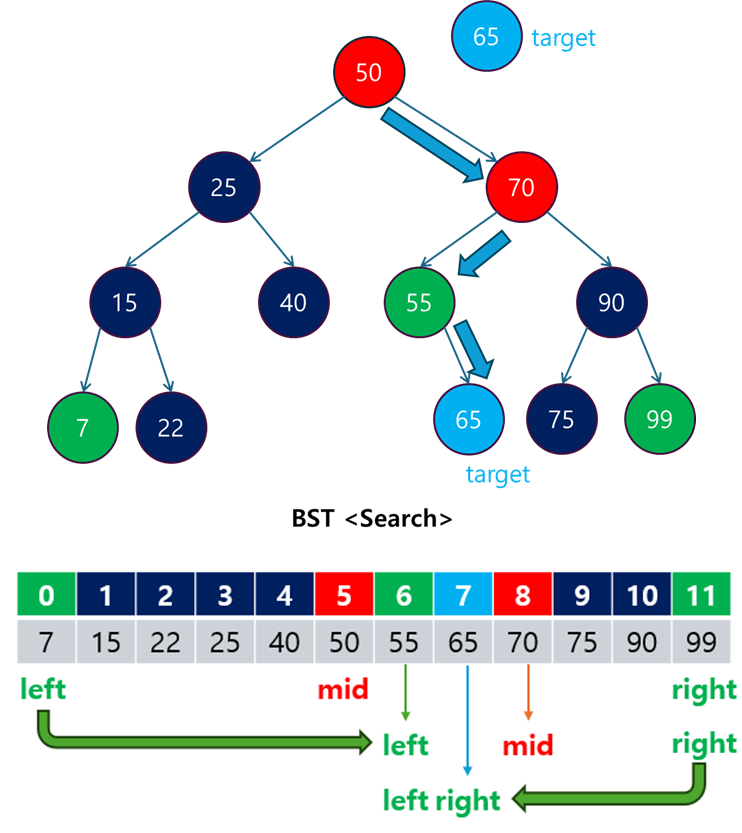
주어진 배열 [7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99]에서 값 65를 찾는 과정을 살펴보겠습니다.

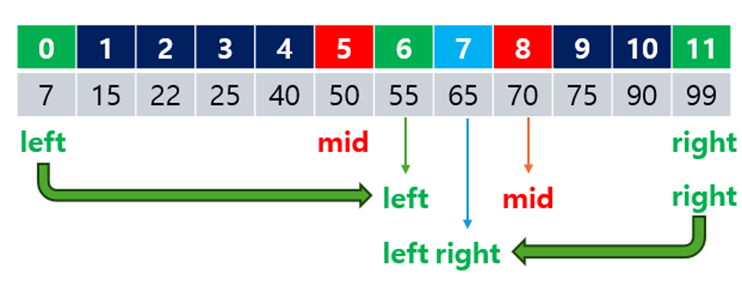
  1. 초기 상태:

    • left = 0, right = 11 (배열의 첫 번째와 마지막 인덱스)
    • mid = (0 + 11) // 2 = 5 (중간값의 인덱스는 5, 중간값은 arr[5] = 50)

  2. 첫 번째 비교: arr[5] = 50이므로, 목표 값 65보다 작습니다. 따라서 left = mid + 1로 갱신하여 탐색 범위를 좁힙니다.

    • left = 6, right = 11
    • mid = (6 + 11) // 2 = 8 (중간값의 인덱스는 8, 중간값은 arr[8] = 70)

  3. 두 번째 비교: arr[8] = 70이므로, 목표 값 65보다 큽니다. 따라서 right = mid - 1로 갱신하여 탐색 범위를 좁힙니다.

    • left = 6, right = 7
    • mid = (6 + 7) // 2 = 6 (중간값의 인덱스는 6, 중간값은 arr[6] = 55)

  4. 세 번째 비교: arr[6] = 55이므로, 목표 값 65보다 작습니다. 따라서 left = mid + 1로 갱신합니다.

    • left = 7, right = 7
    • mid = (7 + 7) // 2 = 7 (중간값의 인덱스는 7, 중간값은 arr[7] = 65)

  5. 결과: 중간값 arr[7] = 65는 목표 값 65와 일치하므로, 탐색이 성공적으로 종료됩니다.

3.3 Binary Search 코드 구현

Python 코드 예시

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1  # 값을 찾지 못한 경우

# 테스트
arr = [7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99]
target = 65
result = binary_search(arr, target)
print(f"Target {target} found at index {result}")  # 출력: Target 65 found at index 7

Java 코드 예시

public class BinarySearchExample {
    public static int binarySearch(int[] arr, int target) {
        int left = 0, right = arr.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (arr[mid] == target) {
                return mid;
            } else if (arr[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;  // 값을 찾지 못한 경우
    }

    public static void main(String[] args) {
        int[] arr = {7, 15, 22, 25, 40, 50, 55, 65, 70, 75, 90, 99};
        int target = 65;
        int result = binarySearch(arr, target);
        if (result != -1) {
            System.out.println("Target " + target + " found at index " + result);
        } else {
            System.out.println("Target not found.");
        }
    }
}

3.4 Binary Search의 시간 복잡도

Binary Search의 시간 복잡도는 O(log n)입니다.

  • 매번 배열을 절반으로 나누기 때문에, 탐색 대상이 되는 배열의 크기가 매우 클 때에도 탐색 시간이 빠르게 줄어듭니다.

이진 탐색은 다음과 같이 작동합니다:

  • 첫 번째 비교에서 배열을 절반으로 나누고,
  • 두 번째 비교에서 남은 절반을 다시 절반으로 나누는 방식으로 진행됩니다.
    • 결과적으로, 탐색 범위가 매번 절반으로 줄어들기 때문에 로그(logarithmic) 복잡도를 갖습니다.

선형 탐색이 O(n)의 복잡도를 가지는 것에 비해, 이진 탐색은 훨씬 더 빠르게 목표 값을 찾을 수 있습니다.

  • 예를 들어, 배열의 크기가 1,000,000일 때 선형 탐색은 최악의 경우 1,000,000번 비교가 필요하지만, 이진 탐색은 20번 미만의 비교로 목표 값을 찾을 수 있습니다.

마무리

이번 포스팅에서는 배열 기반 탐색 알고리즘 중 Two-Pointer와 Binary Search에 대해 살펴보았습니다. 두 알고리즘 모두 효율적으로 탐색을 수행할 수 있는 방법으로, 배열에서 특정 값을 빠르게 찾는 데 중요한 역할을 합니다.

  • Two-Pointer 알고리즘은 정렬된 배열에서 두 포인터를 이용해 특정 조건을 만족하는 값을 찾을 때 유용하며, 시간 복잡도가 O(n)으로 매우 효율적입니다.
  • Binary Search 알고리즘은 배열이 정렬된 상태에서 중간 값을 기준으로 탐색 범위를 반복적으로 좁혀가며 목표 값을 찾는 방식으로, 시간 복잡도는 O(log n)입니다.

다음 포스팅에서는 그래프 및 트리 기반 탐색으로 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)을 다루고 이후에 백트래킹(Backtracking) 알고리즘에 대해 다룰 예정입니다.

profile
Kyung Jae, Cheong
일 때문에 포스팅은 잠시 쉬어요 ㅠ 바쁘다 바빠 모두들 화이팅! // Machine Learning (AI) Engineer & BackEnd Engineer (Entry)
이전 포스트

[알고리즘] 분할 정복(Divide and Conquer) - 개념과 활용

다음 포스트

[알고리즘] 탐색(Search) - DFS(Depth-First Search) & BFS(Breadth-First Search)

0개의 댓글