본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

• 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
  • IDE : IntelliJ IDEA (Ultimate Edition)
  • Java : JDK 21 (corretto-21)
  • Python : 3.9 (conda env)

Graph 알고리즘 - 최소 신장 트리 (Minimum Spanning Tree)

1. Minimum Spanning Tree란?

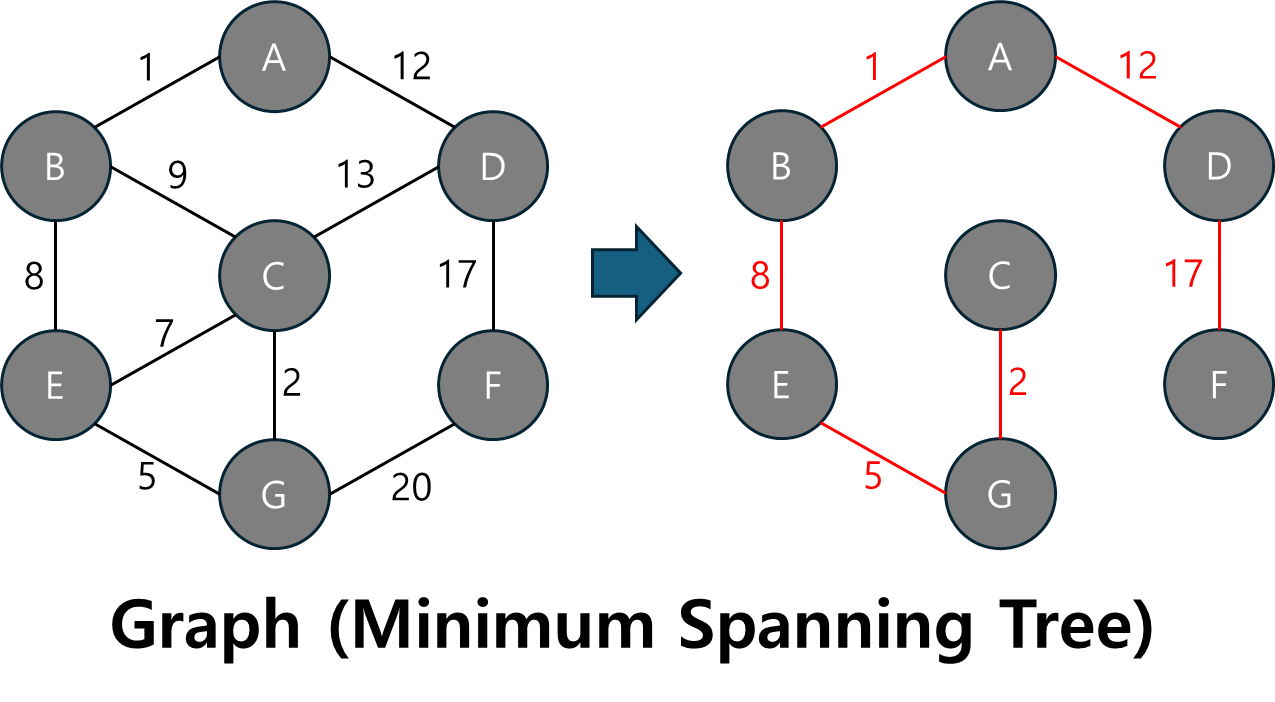
Minimum Spanning Tree(MST)는 가중치가 있는 무향 그래프에서 모든 노드를 연결하는 트리 중 가중치의 합이 가장 작은 트리를 의미합니다.

• 그래프의 모든 노드를 포함하되, 간선의 수가 최소이면서도 각 노드를 연결하는 가중치 합이 가장 적게 되도록 하는 것이 목표입니다.

MST는 네트워크 설계, 경로 최적화 등 여러 분야에서 사용되며, 대표적인 예로는 전기나 수도와 같은 인프라 네트워크 설계, 도로 시스템 최적화, 그리고 클러스터링 문제 등이 있습니다.

MST의 주요 특징은 다음과 같습니다:

• 무향 그래프에만 적용됩니다. (방향성이 없는 간선을 가집니다.)
• 하나의 그래프에는 여러 개의 MST가 존재할 수 있습니다. (최소한의 비용을 가지는 트리는 여러 가지일 수 있습니다.)
• MST의 간선 수는 항상 노드 수 - 1 개입니다.

이러한 MST를 찾기 위해 주로 사용되는 알고리즘은 다음과 같습니다:

1. 크루스칼 알고리즘: 간선을 가중치의 오름차순으로 선택하여 최소 비용으로 연결하는 방식
2. 프림 알고리즘: 특정 시작점에서 시작하여 연결된 노드들 간의 최소 간선을 선택하며 트리를 확장하는 방식

2. 최소 신장 트리 알고리즘 종류 & 특징

최소 신장 트리(MST)를 찾기 위한 대표적인 알고리즘은 크루스칼(Kruskal) 알고리즘과 프림(Prim) 알고리즘입니다. 이 두 알고리즘은 모두 MST를 찾기 위해 사용되지만, 작동 방식과 적합한 그래프 구조에서 차이가 있습니다.

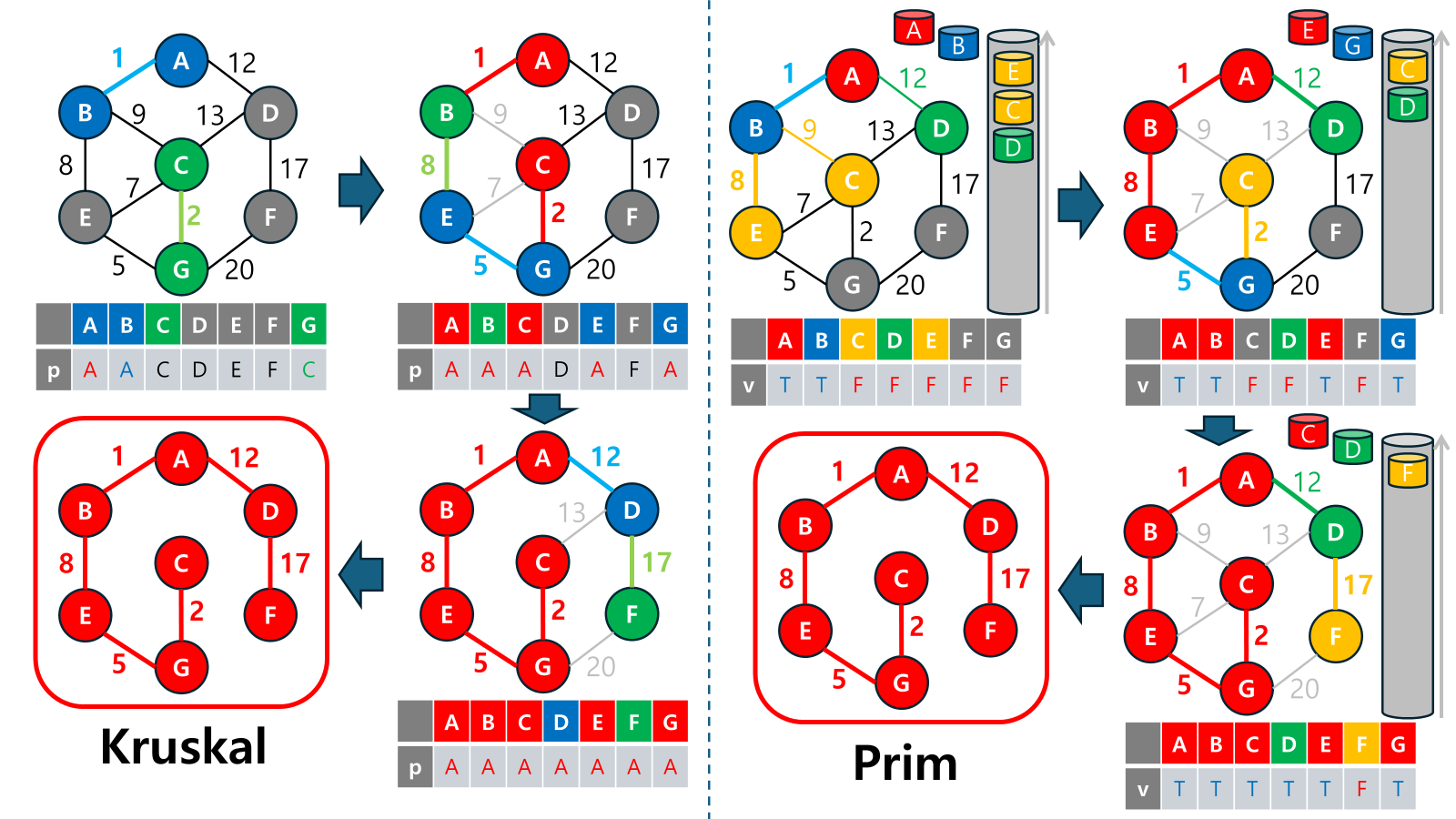
크루스칼(Kruskal) 알고리즘

• 작동 원리: 간선 중심으로 가중치가 낮은 순서대로 선택하며, 사이클이 생기지 않도록 트리를 확장해 나갑니다.
• 특징: 주로 간선 개수가 적은 희소 그래프(sparse graph)에 유리합니다.
• 시간 복잡도: 간선 수를 $E$, 노드 수를 $V$라 할 때, $O(ElogE)$로, 정렬 과정에서 복잡도가 결정됩니다.
• 적용: Union-Find 자료구조를 이용해 사이클을 감지하며, 네트워크 연결 문제에 많이 사용됩니다.

프림(Prim) 알고리즘

• 작동 원리: 특정 시작 노드에서 출발해 인접 노드 중 가중치가 가장 낮은 간선을 선택하여 점진적으로 트리를 확장합니다.
• 특징: 밀집 그래프(dense graph)나 노드 개수가 많을 때 효율적입니다.
• 시간 복잡도: $O(ElogV)$로, 우선순위 큐를 사용하여 간선 가중치를 효율적으로 관리합니다.
• 적용: 네트워크 연결 외에도 최소 비용 경로 탐색 등에 사용됩니다.

알고리즘	주요 특징	시간 복잡도	적합한 그래프 구조
크루스칼 (Kruskal)	간선 선택 방식, 사이클 감지	$O(ElogE)$	희소 그래프 (sparse graph)
프림 (Prim)	노드 중심으로 확장, 우선순위 큐 활용	$O(ElogV)$	밀집 그래프 (dense graph)

3-1. 크루스칼(Kruskal) 알고리즘

Kruskal 알고리즘은 그리디(Greedy) 알고리즘의 한 예로, 최소 가중치 간선부터 하나씩 선택하면서 MST를 형성합니다.

• 이 알고리즘은 간선 기반(edge-based) 방식으로, 모든 간선을 가중치 기준으로 정렬한 후, 가장 낮은 가중치의 간선을 선택하며 트리를 확장해 나갑니다.

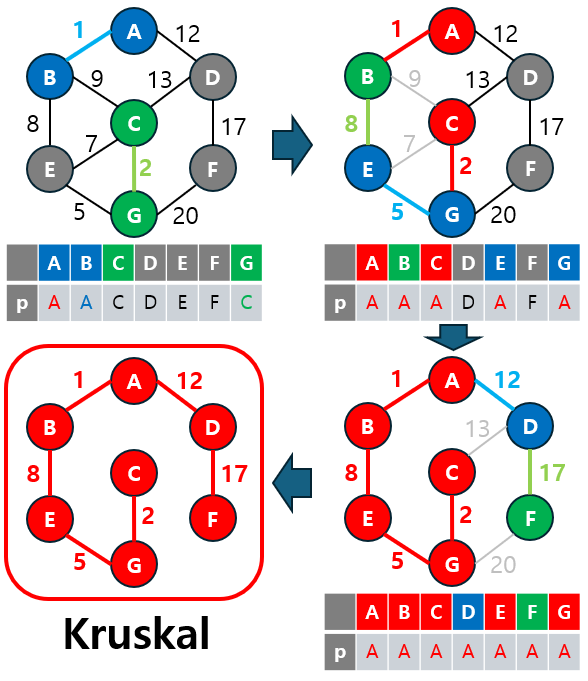
3-1.1 Kruskal 알고리즘 특징

• 간선 중심적 접근 방식: 가중치가 낮은 간선부터 선택해 나가므로, 간선이 많은 경우 정렬 과정이 주요한 시간 소요 요소가 됩니다.
• 사이클 방지: 간선을 선택할 때마다 Union-Find 자료구조를 통해 사이클이 생기는지 여부를 확인합니다. 사이클이 생길 경우 해당 간선을 제외하고 다음 간선으로 넘어갑니다.
• 희소 그래프에 적합: 그래프의 간선 개수가 적을수록 효율적으로 동작합니다.

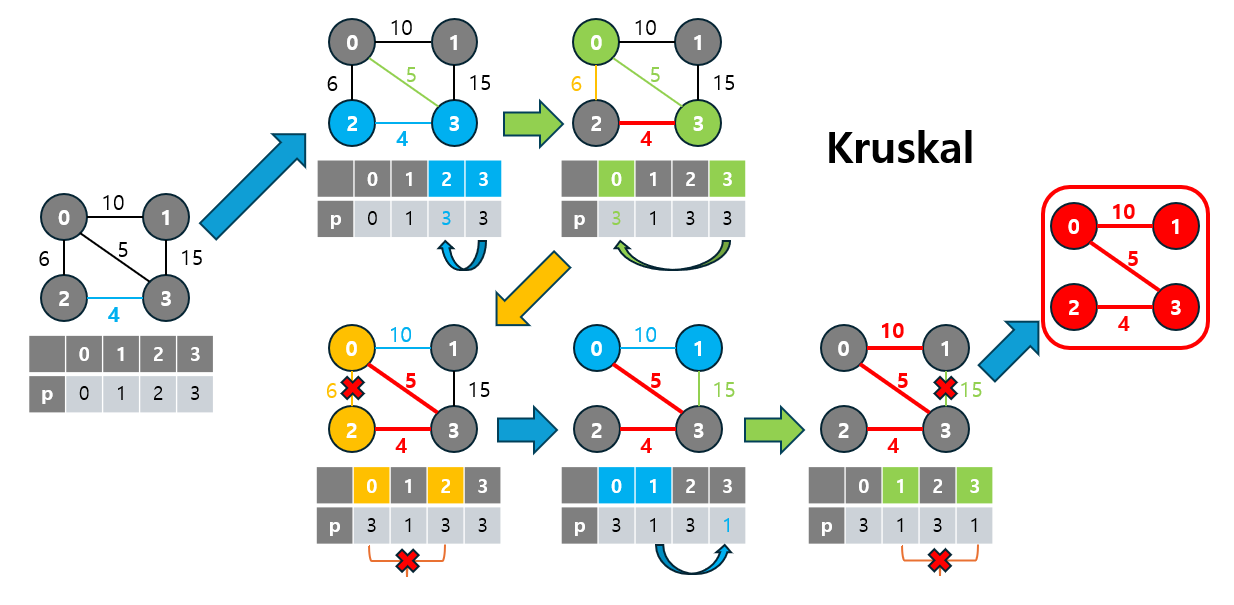
3-1.2 Kruskal 동작 원리

Kruskal 알고리즘의 동작 원리는 다음과 같습니다:

1. 간선 정렬: 모든 간선을 가중치의 오름차순으로 정렬합니다.
2. 간선 선택: 순서대로 간선을 선택하며 사이클을 방지하기 위해 Union-Find 자료구조를 사용합니다.
   • 선택한 간선이 사이클을 형성하지 않는다면 MST에 추가합니다.
   • 선택한 간선이 사이클을 형성한다면 이를 제외하고 다음 간선을 선택합니다.
3. 종료 조건: MST의 간선 수가 $V−1$개가 되면 알고리즘이 종료됩니다. (여기서 V는 노드의 수입니다.)

이 과정을 통해 그래프의 모든 노드를 연결하면서 최소 비용의 신장 트리를 완성할 수 있습니다.

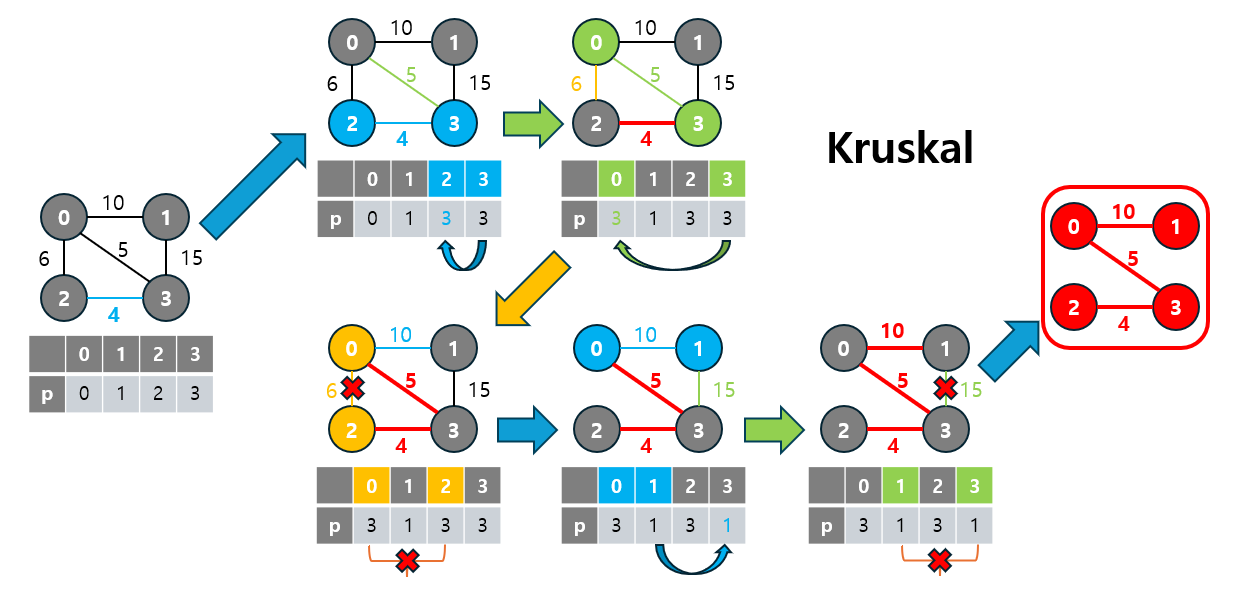
Union-Find 자료구조란?
Union-Find 자료구조는 서로소 집합(disjoint set)을 효율적으로 관리하는 자료구조로, Kruskal 알고리즘에서 사이클을 검출하기 위해 사용됩니다.
이를 통해 간선을 추가할 때 사이클이 생기는지 빠르게 확인할 수 있습니다.

• Find: 특정 노드가 속한 집합의 대표(root) 노드를 찾습니다.
  • Kruskal 알고리즘에서 각 노드가 연결된 집합을 추적하여, 두 노드가 같은 집합에 속하는지 여부를 확인하는 데 사용됩니다.
  • 경로 압축(Path Compression)을 사용해 Find 연산을 최적화할 수 있습니다.
  • 이는 노드를 찾을 때 해당 경로를 최적화하여 다음 검색이 더 빠르게 이뤄지도록 하는 기법입니다.
• Union: 두 집합을 하나의 집합으로 합칩니다.
  • 두 노드가 서로 다른 집합에 속할 경우, 두 집합을 하나로 합쳐 MST에 추가할 수 있도록 합니다.
  • Union 연산에서는 일반적으로 랭크(rank) 기반 또는 크기(size) 기반 최적화 기법을 사용해 트리의 높이를 최소화합니다.
• 이와 같은 Union-Find 자료구조는 Kruskal 알고리즘에서 사이클 검출을 빠르게 수행해 주며, 알고리즘의 시간 효율성을 높이는 데 중요한 역할을 합니다.

3-1.3 Kruskal 코드 구현 (Java, Python)

Java와 Python으로 구현된 Kruskal 알고리즘의 예제는 다음과 같습니다. 이 코드는 Union-Find 자료구조를 활용하여 효율적으로 사이클을 검출하고, MST를 형성합니다.

Java 코드 구현

import java.util.*;

public class Kruskal {

    // 간선을 나타내는 Edge 클래스 - Comparable 인터페이스를 구현하여 간선 가중치 기준으로 정렬 가능
    static class Edge implements Comparable<Edge> {
        int src, dest, weight;
        public Edge(int src, int dest, int weight) {
            this.src = src;
            this.dest = dest;
            this.weight = weight;
        }
        // 가중치 기준 오름차순 정렬을 위한 compareTo 메서드
        public int compareTo(Edge other) {
            return this.weight - other.weight;
        }
    }

    // Union-Find에서 각 노드의 부모를 저장하는 배열
    static int[] parent;

    // Find 연산 - 경로 압축 최적화를 적용하여 트리의 높이를 줄임
    static int find(int i) {
        if (parent[i] != i) {
            parent[i] = find(parent[i]);
        }
        return parent[i];
    }

    // Union 연산 - 두 집합을 병합
    static void union(int x, int y) {
        int xRoot = find(x);
        int yRoot = find(y);
        parent[xRoot] = yRoot;
    }

    // Kruskal 알고리즘 - MST를 생성하고 각 간선 및 최종 가중치 출력
    static void kruskalMST(int V, List<Edge> edges) {
        // 간선 정렬 - 가중치가 낮은 순서대로 정렬
        edges.sort(null);
        parent = new int[V];	// Union-Find 초기화
        for (int i = 0; i < V; i++) parent[i] = i;

        int edgeCount = 0, mstWeight = 0;
        for (Edge edge : edges) {
            // MST 완성 조건 - V-1개의 간선이 선택되면 종료
            if (edgeCount == V - 1) break;

            int x = find(edge.src);
            int y = find(edge.dest);
            if (x != y) {	// 사이클을 형성하지 않으면 간선 선택
                union(x, y);
                edgeCount++;
                mstWeight += edge.weight;
                System.out.println("Selected Edge: " +
                        edge.src + " - " +
                        edge.dest + " : " +
                        edge.weight);
            }
        }
        System.out.println("Total weight of MST: " + mstWeight);
    }

    public static void main(String[] args) {
        int V = 4; // 노드 수
        List<Edge> edges = new ArrayList<>();

        // 간선 추가 (src, dest, weight)
        edges.add(new Edge(0, 1, 10));
        edges.add(new Edge(0, 2, 6));
        edges.add(new Edge(0, 3, 5));
        edges.add(new Edge(1, 3, 15));
        edges.add(new Edge(2, 3, 4));

        // Kruskal 알고리즘 실행
        kruskalMST(V, edges);
    }
}

출력 결과 (Java, Python 동일)

Selected Edge: 2 - 3 : 4
Selected Edge: 0 - 3 : 5
Selected Edge: 0 - 1 : 10
Total weight of MST: 19

Java 코드 구현 설명

위 Java 코드는 Kruskal 알고리즘을 통해 최소 신장 트리(MST)를 찾는 방법을 보여줍니다. 주요 기능은 다음과 같습니다:

1. 간선 정렬: edges.sort(null);를 통해 간선 리스트를 가중치 기준으로 오름차순 정렬합니다.
2. Union-Find 자료구조: find와 union 메서드를 통해 각 노드가 속한 집합을 추적하고, 간선 선택 시 사이클 여부를 검사합니다.
3. MST 형성: 사이클을 형성하지 않는 간선만 선택하여 MST를 완성합니다. 선택된 간선과 총 가중치를 출력해 결과를 확인할 수 있습니다.

이 알고리즘은 $O(E \log E)$의 시간 복잡도를 가지며, 간선이 정렬된 후 간선이 $V−1$개 선택될 때까지 트리를 확장해 나갑니다.

Python 코드 구현

class Edge:
    def __init__(self, src, dest, weight):
        self.src = src
        self.dest = dest
        self.weight = weight

# Find 연산 - 경로 압축을 통해 트리 높이 최적화
def find(parent, i):
    if parent[i] != i:
        parent[i] = find(parent, parent[i])
    return parent[i]

# Union 연산 - 두 집합을 하나로 병합
def union(parent, x, y):
    x_root = find(parent, x)
    y_root = find(parent, y)
    parent[x_root] = y_root

# Kruskal 알고리즘 - MST 생성 및 간선 출력
def kruskal_mst(vertices, edges):
    # 1. 간선 정렬 - 가중치 기준 오름차순
    edges.sort(key=lambda e: e.weight)
    parent = [i for i in range(vertices)]	# Union-Find 초기화
    mst_weight = 0

    for edge in edges:
        x = find(parent, edge.src)
        y = find(parent, edge.dest)

        if x != y:	# 사이클이 없을 경우 간선 선택
            union(parent, x, y)
            mst_weight += edge.weight
            print(f"Selected Edge: {edge.src} - {edge.dest} : {edge.weight}")

    print(f"Total weight of MST: {mst_weight}")

# 테스트 실행
v = 4
edges_list = [
    Edge(0, 1, 10),
    Edge(0, 2, 6),
    Edge(0, 3, 5),
    Edge(1, 3, 15),
    Edge(2, 3, 4),
]

kruskal_mst(v, edges_list)

출력 결과 (Java, Python 동일)

Selected Edge: 2 - 3 : 4
Selected Edge: 0 - 3 : 5
Selected Edge: 0 - 1 : 10
Total weight of MST: 19

Python 코드 구현 설명

위 Python 코드는 Java와 동일한 Kruskal 알고리즘을 사용해 MST를 구성합니다. 주요 구현 방식은 다음과 같습니다:

1. 간선 정렬: edges.sort(key=lambda e: e.weight)로 간선의 가중치를 기준으로 오름차순 정렬합니다.
2. Union-Find 자료구조: find와 union 함수를 사용해 각 노드의 집합을 추적하고, 사이클 검출을 수행합니다.
3. MST 형성: 간선을 하나씩 추가하며 사이클을 형성하지 않는 간선만 선택하여 MST를 형성하고, 선택된 간선과 총 가중치를 출력합니다.

이 Python 구현도 $O(E \log E)$의 시간 복잡도를 가지며, 가중치가 낮은 간선부터 선택하여 MST를 형성해 나가는 과정은 Java와 동일합니다.

3-2. 프림(Prim) 알고리즘

Prim 알고리즘은 그리디(Greedy) 알고리즘의 또 다른 예로, 특정 시작 노드에서 출발하여 인접한 간선 중 가중치가 가장 낮은 간선을 선택하며 트리를 확장해 나가는 방식으로 최소 신장 트리(MST)를 형성합니다.

• 이 알고리즘은 노드 중심(node-based) 방식으로, 선택된 노드들과 연결된 간선들 중에서 가장 낮은 가중치를 가진 간선을 선택해 트리를 확장합니다.

3-2.1 Prim 알고리즘 특징

• 노드 중심적 접근 방식: Prim 알고리즘은 한 노드에서 출발하여 인접 간선을 통해 연결된 노드로 확장해 나가는 방식입니다. 이 과정에서 우선순위 큐(Priority Queue)를 사용해 가중치가 낮은 간선을 효율적으로 관리합니다.
• 밀집 그래프(dense graph)에 적합: 간선이 많은 경우 Prim 알고리즘이 더 효율적으로 동작할 수 있습니다.
• 동작 방식: 시작 노드에서 연결된 간선 중 가장 낮은 가중치의 간선을 선택하며, 선택된 노드 집합을 점진적으로 확장합니다.

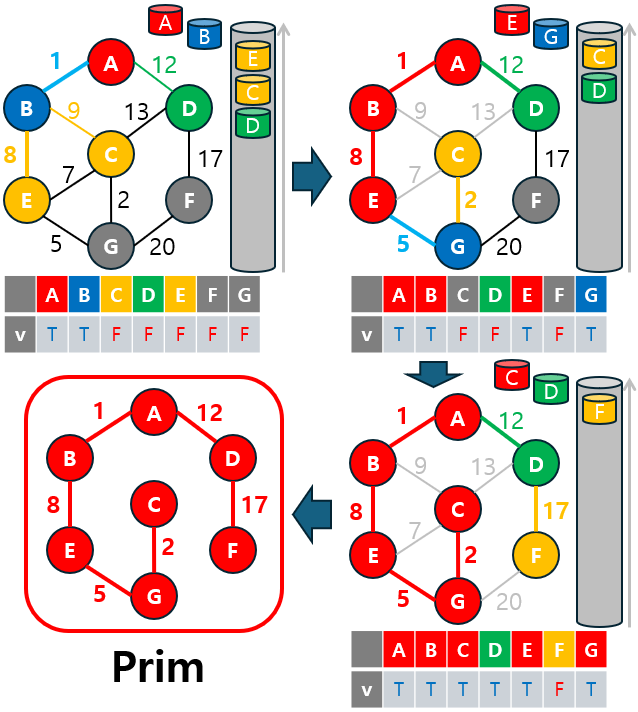
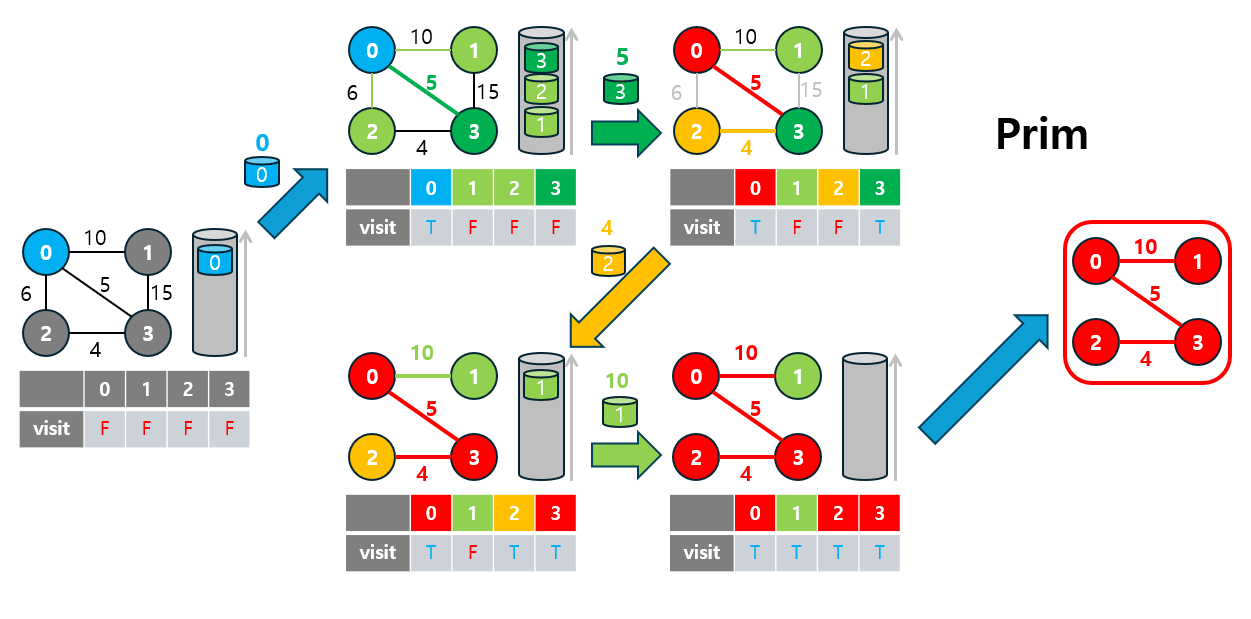
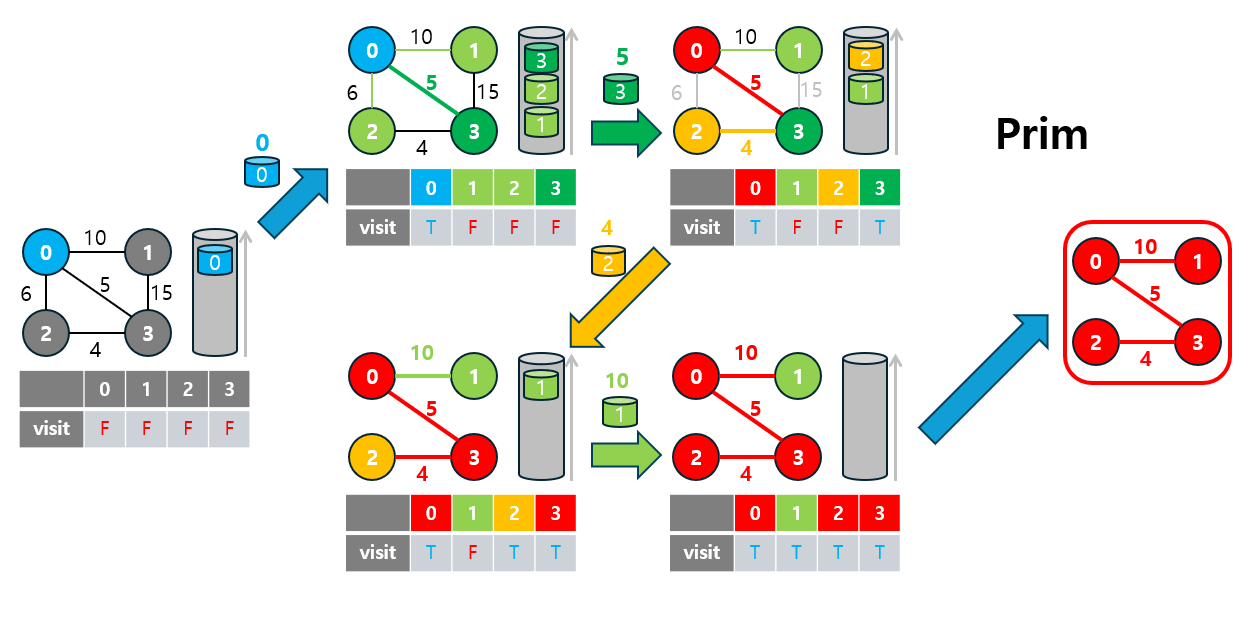
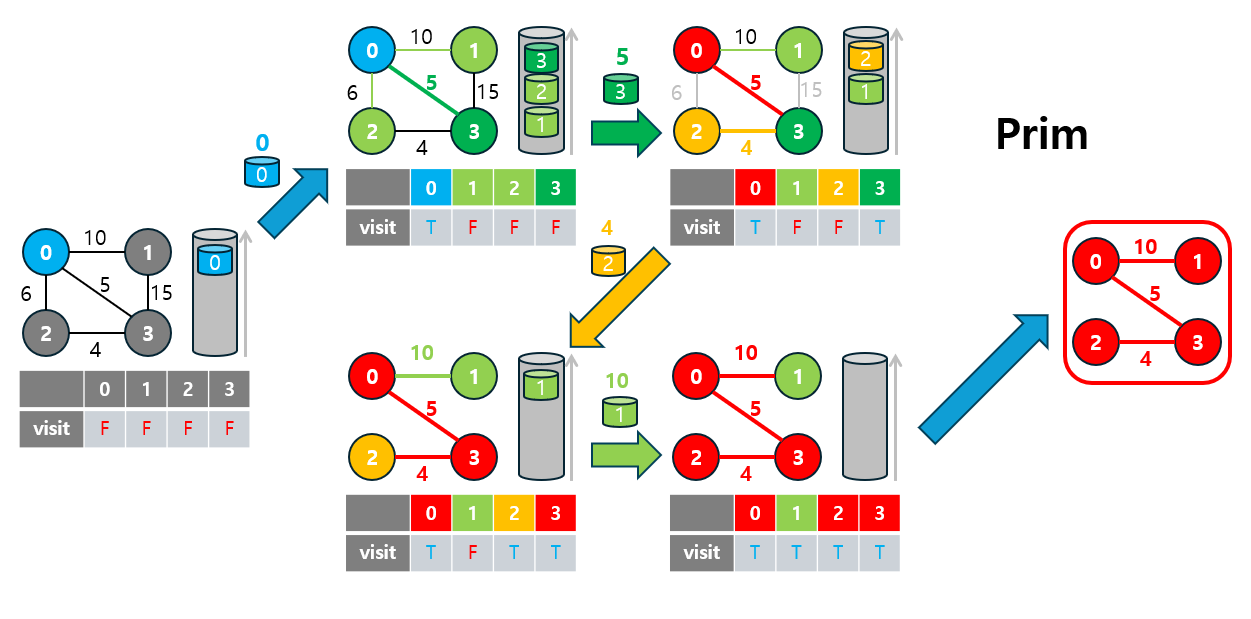
3-2.2 Prim 동작 원리

Prim 알고리즘의 동작 원리는 다음과 같습니다:

1. 시작 노드 선택: 임의의 노드를 시작 노드로 설정하고, 해당 노드에서 출발하는 간선을 탐색합니다.
2. 간선 선택: 시작 노드와 연결된 간선들 중 가장 낮은 가중치를 가진 간선을 선택하여 MST에 추가합니다.
   • 선택된 간선의 목적지 노드를 추가하고, 새로 추가된 노드에 연결된 간선들을 탐색 대상으로 추가합니다.
   • 이 과정에서 우선순위 큐를 사용하여 가중치가 가장 낮은 간선을 선택해 효율성을 높입니다.
3. 종료 조건: 모든 노드가 MST에 포함되면 알고리즘이 종료됩니다.

이 과정을 통해 그래프의 모든 노드를 연결하면서 최소 비용의 신장 트리를 완성할 수 있습니다.

3-2.3 Prim 코드 구현 (Java, Python)

Java와 Python으로 구현된 Prim 알고리즘의 예제는 다음과 같습니다.

• 이 코드는 우선순위 큐(Priority Queue)를 활용하여 가중치가 낮은 간선을 효율적으로 선택하며 MST를 형성합니다.

Java 코드 구현

import java.util.*;

public class Prim {

    static class Edge implements Comparable<Edge> {
        int dest, weight;
        public Edge(int dest, int weight) {
            this.dest = dest;
            this.weight = weight;
        }
        public int compareTo(Edge other) {
            return this.weight - other.weight;
        }
    }

    static void primMST(List<List<Edge>> graph, int V) {
        boolean[] inMST = new boolean[V];
        Queue<Edge> pq = new PriorityQueue<>();
        pq.add(new Edge(0,0)); // 시작 노드는 가중치 0으로 추가
        int mstWeight = 0;

        while (!pq.isEmpty()) {
            Edge edge = pq.poll();
            int node = edge.dest;

            // 노드가 MST에 포함되었는지 확인
            if (inMST[node]) continue;

            // 노드를 MST에 추가하고 가중치 누적
            inMST[node] = true;
            mstWeight += edge.weight;
            System.out.println("Selected Node: " + node +
                    " with edge weight: " + edge.weight);

            // 인접 노드들을 탐색
            for (Edge adjacent : graph.get(node)) {
                if (!inMST[adjacent.dest]) {
                    pq.add(adjacent);
                }
            }
        }
        System.out.println("Total weight of MST: " + mstWeight);
    }

    public static void main(String[] args) {
        int V = 4; // 노드 수
        List<List<Edge>> graph = new ArrayList<>();

        for (int i = 0; i < V; i++) graph.add(new ArrayList<>());

        // 양방향 간선 추가 (src, dest, weight)
        graph.get(0).add(new Edge(1, 10));
        graph.get(1).add(new Edge(0, 10));

        graph.get(0).add(new Edge(2, 6));
        graph.get(2).add(new Edge(0, 6));

        graph.get(0).add(new Edge(3, 5));
        graph.get(3).add(new Edge(0, 5));

        graph.get(1).add(new Edge(3, 15));
        graph.get(3).add(new Edge(1, 15));

        graph.get(2).add(new Edge(3, 4));
        graph.get(3).add(new Edge(2, 4));

        // Prim 알고리즘 실행
        primMST(graph, V);
    }
}

출력 결과 (Java, Python 동일)

Selected Node: 0 with edge weight: 0
Selected Node: 3 with edge weight: 5
Selected Node: 2 with edge weight: 4
Selected Node: 1 with edge weight: 10
Total weight of MST: 19

Java 코드 구현 설명
위 Java 코드는 Prim 알고리즘을 통해 MST를 생성하는 방법을 보여줍니다. 주요 기능은 다음과 같습니다:

1. 우선순위 큐 사용: PriorityQueue를 통해 가중치가 낮은 간선을 우선으로 선택합니다.
2. MST 확장: MST에 포함되지 않은 노드에 연결된 간선을 탐색하여 우선순위 큐에 추가하며, 노드 중심으로 트리를 확장합니다.
3. MST 형성 완료: 모든 노드가 MST에 포함되면 총 가중치가 출력됩니다.

이 알고리즘은 $O(E log V)$의 시간 복잡도를 가지며, Prim 알고리즘의 특징인 노드 중심의 확장 방식을 잘 보여줍니다.

Python 코드 구현

import heapq

def prim_mst(graph, vertices):
    in_mst = [False] * vertices
    pq = [(0, 0)] # (가중치, 노드)
    mst_weight = 0

    while pq:
        weight, node = heapq.heappop(pq)

        # 노드가 이미 MST에 포함되었는지 확인
        if in_mst[node]:
            continue

        # 노드를 MST에 추가하고 가중치 누적
        in_mst[node] = True
        mst_weight += weight
        print(f"Selected Node: {node} with edge weight: {weight}")

        # 인접 노드들을 탐색
        for adj_weight, adj_node in graph[node]:
            if not in_mst[adj_node]:
                heapq.heappush(pq, (adj_weight, adj_node))

    print(f"Total weight of MST: {mst_weight}")

# 테스트 실행
v = 4
graph = {
    0: [(10, 1), (6, 2), (5, 3)],
    1: [(10, 0), (15, 3)],
    2: [(6, 0), (4, 3)],
    3: [(5, 0), (15, 1), (4, 2)],
}

prim_mst(graph, v)

출력 결과 (Java, Python 동일)

Selected Node: 0 with edge weight: 0
Selected Node: 3 with edge weight: 5
Selected Node: 2 with edge weight: 4
Selected Node: 1 with edge weight: 10
Total weight of MST: 19

Python 코드 구현 설명
위 Python 코드는 Prim 알고리즘을 사용해 MST를 구성합니다. 주요 기능은 다음과 같습니다:

1. 우선순위 큐 사용: heapq 모듈을 통해 가중치가 낮은 간선을 우선으로 선택합니다.
2. MST 확장: MST에 포함되지 않은 노드와 연결된 간선을 탐색하여 우선순위 큐에 추가하며, 노드 중심으로 트리를 확장합니다.
3. MST 형성 완료: 모든 노드가 MST에 포함되면 총 가중치를 출력하여 결과를 확인합니다.

Python 구현에서도 $O(E log V)$의 시간 복잡도를 가지며, Java와 동일한 노드 중심의 트리 확장 방식으로 MST를 형성합니다.

4. Minimum Spanning Tree 비교 및 선택 기준

Kruskal과 Prim 알고리즘은 모두 MST를 찾기 위한 대표적인 방법이지만, 각각의 특성과 장단점이 있어 상황에 맞는 알고리즘을 선택하는 것이 중요합니다.

아래는 두 알고리즘의 주요 차이점과 선택 기준을 정리한 표입니다.

알고리즘	시간 복잡도	주요 특징	적합한 그래프 구조
Kruskal	$O(ElogE)$	간선 중심, Union-Find로 사이클 감지	간선이 적은 경우 (희소 그래프)
Prim	$O(ElogV)$	노드 중심, 우선순위 큐로 인접 간선 선택	노드 수가 많고 간선이 많은 경우 (밀집 그래프)

• Kruskal 알고리즘은 간선의 가중치를 기준으로 정렬하고 사이클을 감지해 트리를 형성하는 방식이기 때문에, 간선의 수가 적은 그래프에서 효율적입니다. 또한, 그래프가 연결되어 있지 않더라도 사용할 수 있습니다.
• Prim 알고리즘은 특정 노드에서 시작해 트리를 확장하는 방식으로, 간선이 많은 밀집 그래프에서 효율적입니다. 주로 그래프가 연결된 상황에서 사용하는 것이 일반적입니다.

따라서 그래프의 간선 밀도와 노드 수에 따라 두 알고리즘 중 적합한 방식을 선택하는 것이 좋습니다.

마무리

Minimum Spanning Tree(MST)는 그래프에서 모든 노드를 연결하면서도 가중치의 합이 최소가 되도록 트리를 구성하는 핵심 개념입니다. MST는 네트워크 최적화, 경로 탐색, 클러스터링 문제 등 다양한 분야에서 널리 활용됩니다.

본 포스팅에서는 Kruskal 알고리즘과 Prim 알고리즘을 통해 MST를 구성하는 방법을 살펴보았고, 각 알고리즘의 특징과 코드 구현을 통해 작동 원리를 살펴보았습니다.

• 두 알고리즘의 장단점과 선택 기준을 통해, 그래프 구조 및 특성에 따라 두 알고리즘 중 적합한 방식을 선택하는 것이 좋습니다.