
본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.
- 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
- IDE : IntelliJ IDEA (Ultimate Edition)
- Java : JDK 21 (corretto-21)
- Python : 3.9 (conda env)
Graph 알고리즘 - 최단 경로 (Shortest Path)
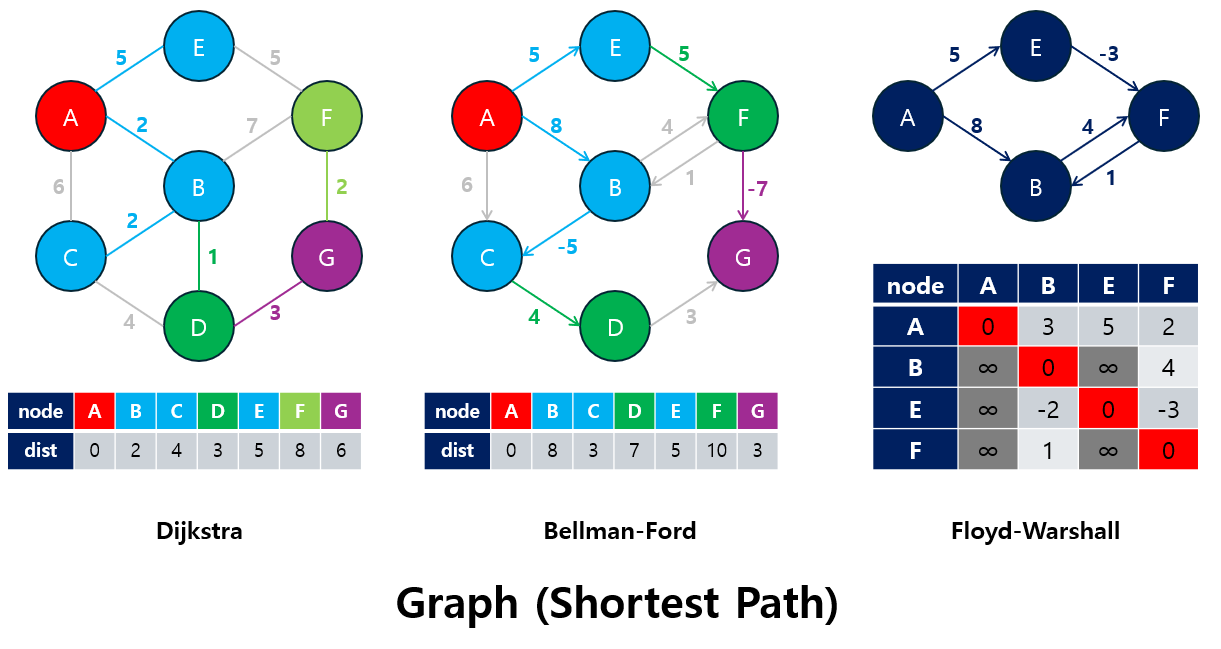
1. Graph Shortest Path 알고리즘이란?
그래프(Graph)는 정점(Vertex)과 간선(Edge)으로 구성된 자료 구조로, 다양한 실제 문제를 해결하는 데 사용됩니다.
- 예를 들어, 도시 간 최단 거리 찾기, 네트워크 패킷의 최적 경로 탐색, 웹 페이지 간 연결성 분석 등이 그래프 기반 문제에 해당합니다.
- [자료구조] NonLinear Data - Graph [Part1. 개요 (구성 요소 & 분류)]
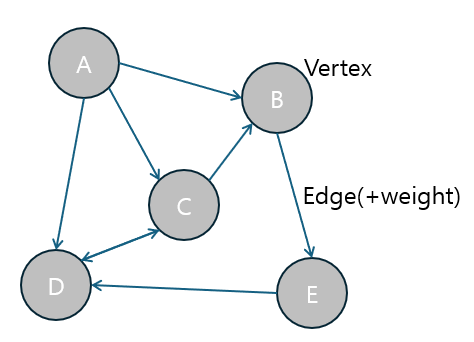
Shortest Path (최단 경로) 알고리즘은 이러한 그래프에서 두 정점 사이의 경로 중, 가장 짧은 경로를 찾는 알고리즘입니다.
- 여기서 경로의 길이는 일반적으로 간선의 가중치(비용, 거리 등) 합으로 정의됩니다.
- 이 알고리즘은 경로 최적화, 비용 최소화 등 다양한 목적을 달성하는 데 중요한 역할을 합니다.
최단 경로 알고리즘은 주로 다음과 같은 상황에서 유용합니다:
- 네비게이션 시스템: 두 지점 간의 최단 경로 계산
- 네트워크 라우팅: 데이터 패킷의 최적화된 전달 경로 결정
- 소셜 네트워크 분석: 특정 노드 간의 관계 경로 찾기
다양한 최단 경로 알고리즘이 존재하며, 각각의 알고리즘은 그래프의 특성과 목적에 따라 다양한 조건에서 사용됩니다.
이번 포스팅에서는 대표적인 최단 경로 알고리즘인 다익스트라(Dijkstra), 벨만-포드(Bellman-Ford), 플로이드-워셜(Floyd-Warshall) 알고리즘을 살펴보고, 각 알고리즘의 특징과 사용 방법에 대해 알아보겠습니다.
2. 최단 경로 알고리즘 종류 & 특징
그래프에서 최단 경로를 찾는 알고리즘은 그래프의 특성(예: 가중치의 음수 포함 여부, 모든 쌍에 대해 최단 경로를 구해야 하는지 등)에 따라 다르게 적용됩니다.
- 대표적인 최단 경로 알고리즘으로는 다익스트라(Dijkstra), 벨만-포드(Bellman-Ford), 플로이드-워셜(Floyd-Warshall)이 있으며, 각 알고리즘은 다음과 같은 특징을 가지고 있습니다.
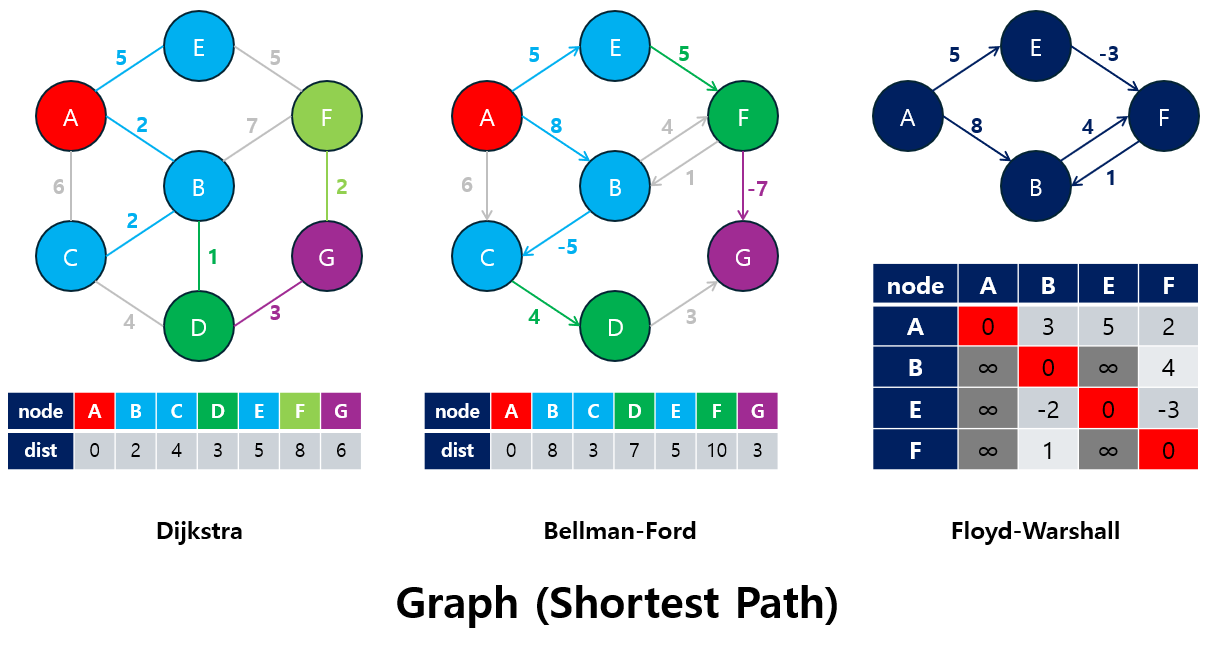
-
다익스트라 알고리즘 (Dijkstra's Algorithm)
- 특징: 특정 시작점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘입니다.
- 가중치 조건: 양수 가중치만 처리할 수 있습니다. 음수 가중치가 있는 그래프에서는 사용할 수 없습니다.
- 시간 복잡도:
- 인접 리스트를 사용한 경우:
- 인접 행렬을 사용한 경우:
- 사용 사례: 네비게이션 시스템, 지도에서의 최단 경로 계산 등
- 제약 사항:
- 음수 가중치가 있는 그래프에서는 사용할 수 없습니다.
- 규모가 큰 그래프에서는 성능이 떨어질 수 있습니다.
-
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
- 특징: 특정 시작점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘입니다.
- 음수 가중치가 있는 그래프도 처리할 수 있으며, 음수 사이클을 감지할 수 있습니다.
- 가중치 조건: 양수 및 음수 가중치를 모두 처리할 수 있습니다.
- 시간 복잡도: (
V는 정점의 개수,E는 간선의 개수) - 사용 사례: 금융 거래 네트워크, 주식 거래에서의 차익 거래 탐색 등
- 제약 사항:
- 시간 복잡도가 높아 큰 그래프에서는 비효율적입니다.
- 음수 사이클이 존재하는 경우 경로를 계산할 수 없으므로 음수 사이클을 탐지하는 추가 과정이 필요합니다.
- 특징: 특정 시작점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘입니다.
-
플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
- 특징: 모든 정점 쌍 간의 최단 경로를 구하는 알고리즘으로, 동적 계획법(Dynamic Programming)을 사용합니다.
- 가중치 조건: 양수 및 음수 가중치를 모두 처리할 수 있습니다.
- 단, 음수 사이클이 있는 경우 올바른 결과를 보장할 수 없습니다.
- 시간 복잡도:
- 사용 사례: 네트워크 최적화, 사회적 거리 계산, 모든 노드 간의 최단 거리 계산이 필요한 경우
- 제약 사항:
- 시간 복잡도가 높아 큰 그래프에는 적합하지 않습니다.
- 음수 사이클이 존재할 경우 결과가 왜곡될 수 있습니다.
요약
| 알고리즘 | 목적 | 가중치 조건 | 시간 복잡도 | 음수 사이클 감지 |
|---|---|---|---|---|
| 다익스트라 | 시작점 -> 모든 정점 최단 경로 | 양수만 가능 | 불가 | |
| 벨만-포드 | 시작점 -> 모든 정점 최단 경로 | 양수 및 음수 가능 | 가능 | |
| 플로이드-워셜 | 모든 쌍 간의 최단 경로 | 양수 및 음수 가능 | 불가 |
3-1. Dijkstra Algorithm
다익스트라(Dijkstra) 알고리즘은 특정 시작점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘입니다.
- 경로의 가중치가 모두 양수일 때만 정확하게 동작하며, 음수 가중치가 존재할 경우 사용하지 않습니다.
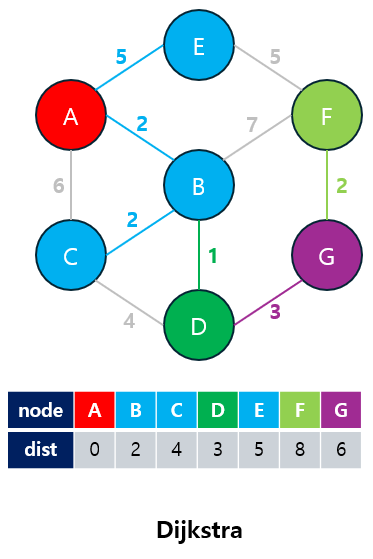
3-1.1 Dijkstra 알고리즘 특징
- 적용 조건: 양수 가중치가 있는 그래프
- 제약 사항: 음수 가중치가 있는 그래프에서는 사용 불가
- 주요 사용 사례: 네비게이션 시스템, 지도에서의 경로 찾기, 네트워크 경로 최적화 등
- 시간 복잡도:
- 인접 리스트를 사용하고 우선순위 큐를 활용하는 경우:
- 인접 행렬을 사용하는 경우:
- 여기서
V는 정점의 개수,E는 간선의 개수입니다.
다익스트라 알고리즘은 간선 개수에 비해 정점 개수가 많을 때 인접 리스트와 우선순위 큐를 사용하는 것이 더 효율적입니다.
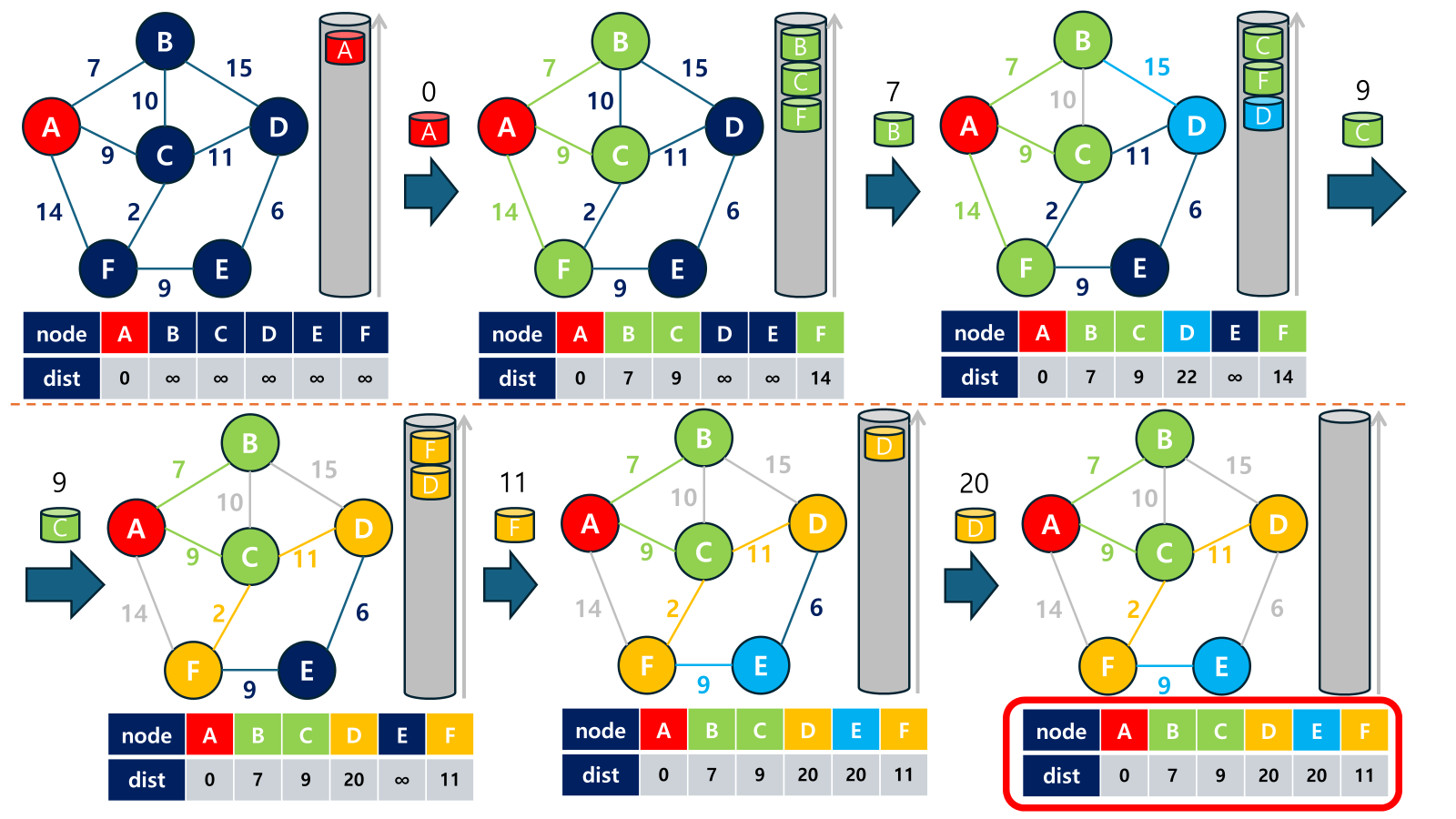
3-1.2 Dijkstra 동작 원리
다익스트라 알고리즘은 탐욕적(greedy) 접근 방식을 사용하여 시작점에서 가장 가까운 정점부터 차례로 최단 거리를 결정합니다. 다음은 기본적인 동작 원리입니다:
- 초기화: 시작 정점의 거리를
0으로 설정하고, 나머지 정점들의 거리는 무한대(혹은 MAX 값)로 설정합니다. - 방문: 방문하지 않은 정점 중 현재 최단 거리가 가장 짧은 정점을 선택하여 방문합니다.
- 갱신: 선택한 정점과 인접한 정점들의 거리를 확인하고, 기존 경로보다 짧은 경로가 발견되면 해당 정점의 최단 거리를 갱신합니다.
- 반복: 모든 정점을 방문할 때까지 2~3번의 과정을 반복합니다.
이 과정을 통해 시작 정점에서 다른 모든 정점으로의 최단 경로가 결정됩니다.
3-1.3 Dijkstra 예제 코드 (Java & Python)
Java 예제 코드
import java.util.*;
public class DijkstraAlgorithm {
static class Edge {
String target; // 연결된 대상 노드
int weight; // 간선 가중치
Edge(String target, int weight) {
this.target = target;
this.weight = weight;
}
}
static Map<String, Integer> dijkstra(String start,
Map<String, List<Edge>> graph) {
// 최단 거리 저장을 위한 맵 초기화 (출력 순서 정렬을 위해 TreeMap 사용)
Map<String, Integer> distances = new TreeMap<>();
for (String node : graph.keySet()) {
distances.put(node, Integer.MAX_VALUE); // 최대값으로 초기화
}
distances.put(start, 0); // 시작 노드의 거리는 0으로 설정
// 우선순위 큐를 사용해 최단 거리가 가장 짧은 노드부터 탐색
Queue<Edge> pq = new PriorityQueue<>(Comparator.comparing(e -> e.weight));
pq.offer(new Edge(start, 0));
while (!pq.isEmpty()) {
Edge current = pq.poll();
String currNode = current.target;
int currDist = current.weight;
// 이미 처리된 노드라면 스킵
if (currDist > distances.get(currNode)) continue;
// 인접 노드들의 거리 갱신
for (Edge edge : graph.get(currNode)) {
String nextNode = edge.target;
int newDist = currDist + edge.weight;
// 최단 거리 갱신 시 우선순위 큐에 추가
if (newDist < distances.get(nextNode)) {
distances.put(nextNode, newDist);
pq.add(new Edge(nextNode, newDist));
}
}
}
return distances;
}
public static void main(String[] args) {
// 그래프 정의
Map<String, List<Edge>> graph = new HashMap<>();
graph.put("A", Arrays.asList(
new Edge("B", 7),
new Edge("C", 9),
new Edge("F", 14)));
graph.put("B", Arrays.asList(
new Edge("A", 7),
new Edge("C", 10),
new Edge("D", 15)));
graph.put("C", Arrays.asList(
new Edge("A", 9),
new Edge("B", 10),
new Edge("D", 11),
new Edge("F", 2)));
graph.put("D", Arrays.asList(
new Edge("B", 15),
new Edge("C", 11),
new Edge("E", 6)));
graph.put("E", Arrays.asList(
new Edge("D", 6),
new Edge("F", 9)));
graph.put("F", Arrays.asList(
new Edge("A", 14),
new Edge("C", 2),
new Edge("E", 9)));
// 다익스트라 알고리즘 수행
String start = "A";
Map<String, Integer> distances = dijkstra(start, graph);
// 최단 거리 출력
System.out.println("Shortest distances from node " + start + ":");
for (Map.Entry<String, Integer> entry : distances.entrySet()) {
System.out.println(entry.getKey() + ": " + entry.getValue());
}
}
}Java: dijkstra 메서드는 시작 노드와 그래프의 인접 리스트를 받아 최단 거리 배열을 반환합니다.
- 우선순위 큐(PriorityQueue)를 사용하여 방문하지 않은 정점 중 최단 거리가 가장 짧은 정점을 효율적으로 선택합니다.
Python 예제 코드
import heapq
def dijkstra(start, graph):
# 최단 거리 저장 딕셔너리 초기화
distances = {node: float('inf') for node in graph}
distances[start] = 0
pq = [(0, start)] # 우선순위 큐 초기화 (거리, 노드)
while pq:
current_distance, current_node = heapq.heappop(pq)
# 이미 처리된 노드라면 스킵
if current_distance > distances[current_node]:
continue
# 인접 노드들의 거리 갱신
for neighbor, weight in graph[current_node]:
distance = current_distance + weight
# 최단 거리 갱신 시 우선순위 큐에 추가
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(pq, (distance, neighbor))
return distances
# 그래프 정의
graph = {
'A': [('B', 7), ('C', 9), ('F', 14)],
'B': [('A', 7), ('C', 10), ('D', 15)],
'C': [('A', 9), ('B', 10), ('D', 11), ('F', 2)],
'D': [('B', 15), ('C', 11), ('E', 6)],
'E': [('D', 6), ('F', 9)],
'F': [('A', 14), ('C', 2), ('E', 9)]
}
# 다익스트라 알고리즘 수행
start_node = 'A'
distances = dijkstra(start_node, graph)
# 최단 거리 출력
print("Shortest distances from node A:")
for node in sorted(distances):
print(f"{node}: {distances[node]}")Python: dijkstra 함수는 힙(heapq)을 사용하여 우선순위 큐 역할을 하며, 각 정점에서의 최단 경로를 계산합니다.
graph는 인접 리스트 형식으로 정의되어 있으며,distances딕셔너리를 통해 각 노드까지의 최단 거리를 저장합니다.
출력 결과 (Java, Python 동일)
Shortest distances from node A:
A: 0
B: 7
C: 9
D: 20
E: 20
F: 11
3-2. Bellman-Ford Algorithm
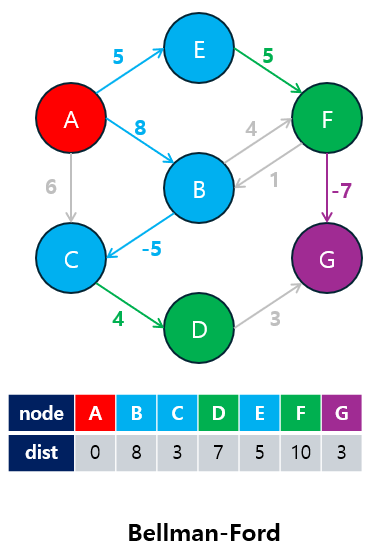
벨만-포드(Bellman-Ford) 알고리즘은 특정 시작점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘입니다.
- 음수 가중치를 포함한 그래프에서도 사용할 수 있으며, 음수 사이클을 탐지하는 기능이 있습니다.
3-2.1 Bellman-Ford 알고리즘 특징
- 적용 조건: 양수 및 음수 가중치를 모두 가진 그래프
- 제약 사항: 음수 사이클이 있는 경우, 무한히 작은 값으로 최단 거리를 갱신하게 되어 유효한 최단 경로를 구할 수 없습니다.
- 주요 사용 사례: 금융 거래 네트워크에서의 차익 거래 탐색, 음수 가중치가 존재할 수 있는 네트워크 경로 탐색, 등
- 시간 복잡도: , 여기서
V는 정점의 개수,E는 간선의 개수입니다.
벨만-포드 알고리즘은 다익스트라 알고리즘에 비해 시간 복잡도가 높지만, 음수 가중치를 처리할 수 있어 유용합니다.
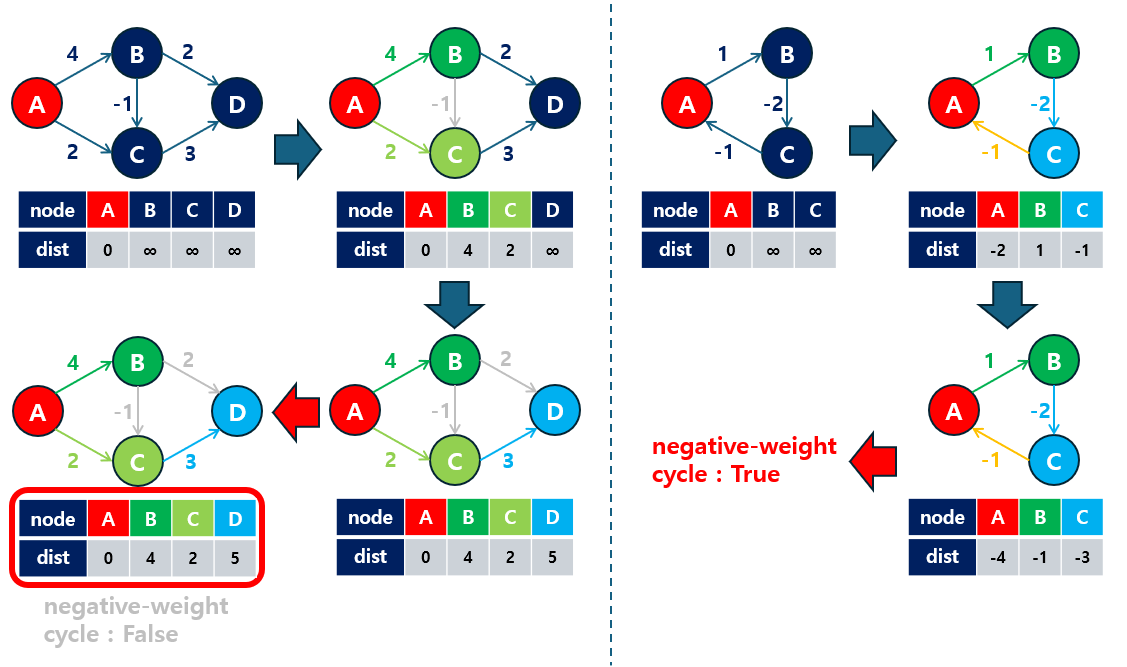
3-2.2 Bellman-Ford 동작 원리
벨만-포드 알고리즘은 모든 간선을 반복적으로 확인하여 최단 거리를 갱신하는 방식으로 동작합니다. 다음은 기본적인 동작 원리입니다:
- 초기화: 시작 정점의 거리를
0으로 설정하고, 나머지 정점들의 거리는 무한대(혹은 MAX 값)로 설정합니다. - 반복 갱신: 모든 간선을 확인하여, 현재 간선을 통해 더 짧은 경로가 발견되면 해당 경로로 거리 갱신을 수행합니다. 이 과정은 총
V-1번 반복합니다 (V는 정점의 개수). - 음수 사이클 탐지:
V-1번 반복 후에도 거리가 갱신되는 간선이 있으면, 해당 그래프에는 음수 사이클이 존재한다고 판단할 수 있습니다.
3-2.3 Bellman-Ford 예제 코드 (Java & Python)
Java 예제 코드
import java.util.*;
public class BellmanFordAlgorithm {
static class Edge {
String source, target;
int weight;
Edge(String source, String target, int weight) {
this.source = source;
this.target = target;
this.weight = weight;
}
}
static Map<String, Integer> bellmanFord(String start,
List<Edge> edges,
Set<String> nodes) {
// 최단 거리 저장을 위한 맵 초기화 (각 노드 거리를 무한대로 설정)
Map<String, Integer> distances = new HashMap<>();
for (String node : nodes) {
distances.put(node, Integer.MAX_VALUE); // 최대값으로 초기화
}
distances.put(start, 0); // 시작 노드의 거리는 0으로 설정
// V-1번 반복하여 모든 간선을 탐색 및 거리 갱신
for (int i = 0; i < nodes.size() - 1; i++) {
for (Edge edge : edges) {
// 무한대가 아닌 경우에만 거리 갱신
if (distances.get(edge.source) != Integer.MAX_VALUE) {
int newDist = distances.get(edge.source) + edge.weight;
if (newDist < distances.get(edge.target)) {
distances.put(edge.target, newDist);
}
}
}
}
// 음수 사이클 존재 여부 확인
for (Edge edge : edges) {
if (distances.get(edge.source) != Integer.MAX_VALUE
&& distances.get(edge.source) + edge.weight < distances.get(edge.target)) {
System.out.println("Graph contains a negative-weight cycle.");
return null; // 음수 사이클이 있으면 null 반환
}
}
return distances; // 최단 거리 반환
}
public static void main(String[] args) {
// 예시 1: 음수 가중치가 있지만 음수 사이클이 없는 그래프
Set<String> nodes = new HashSet<>(Arrays.asList("A", "B", "C", "D"));
List<Edge> edges = Arrays.asList(
new Edge("A", "B", 4),
new Edge("A", "C", 2),
new Edge("B", "C", -1),
new Edge("B", "D", 2),
new Edge("C", "D", 3)
);
System.out.println("===================");
String start = "A";
Map<String, Integer> distances = bellmanFord(start, edges, nodes);
if (distances != null) {
System.out.println("Shortest distances from node " + start + ":");
for (Map.Entry<String, Integer> entry : distances.entrySet()) {
System.out.println(entry.getKey() + ": " + entry.getValue());
}
}
// 예시 2: 음수 사이클이 있는 그래프
System.out.println("===================");
Set<String> nodes2 = new HashSet<>(Arrays.asList("A", "B", "C"));
List<Edge> edges2 = Arrays.asList(
new Edge("A", "B", 1),
new Edge("B", "C", -2),
new Edge("C", "A", -1)
);
String start2 = "A";
Map<String, Integer> distances2 = BellmanFordAlgorithm.bellmanFord(start2, edges2, nodes2);
if (distances2 != null) {
System.out.println("Shortest distances from node " + start2 + ":");
for (Map.Entry<String, Integer> entry : distances2.entrySet()) {
System.out.println(entry.getKey() + ": " + entry.getValue());
}
}
}
}
bellmanFord메서드는 시작 노드, 간선 리스트, 모든 노드 집합을 입력으로 받아 최단 거리 맵을 반환합니다.- 모든 간선을
V-1번 반복하며 최단 거리를 갱신하고, 마지막 추가 반복에서 음수 사이클이 있는 경우null을 반환하여 경고 메시지를 출력합니다.
Python 예제 코드
def bellman_ford(start, edges, nodes):
# 최단 거리 저장 딕셔너리 초기화 (각 노드 거리를 무한대로 설정)
distances = {node: float('inf') for node in nodes}
distances[start] = 0
# V-1번 반복하여 모든 간선을 탐색 및 거리 갱신
for _ in range(len(nodes) - 1):
for source, target, weight in edges:
if distances[source] != float('inf') \
and distances[source] + weight < distances[target]:
distances[target] = distances[source] + weight
# 음수 사이클 존재 여부 확인
for source, target, weight in edges:
if distances[source] != float('inf') \
and distances[source] + weight < distances[target]:
print("Graph contains a negative-weight cycle.")
return None # 음수 사이클이 있으면 None 반환
return distances
# 예시 1: 음수 가중치가 있지만 음수 사이클이 없는 그래프
nodes = {"A", "B", "C", "D"}
edges = [
("A", "B", 4),
("A", "C", 2),
("B", "C", -1),
("B", "D", 2),
("C", "D", 3)
]
print("===================")
start_node = "A"
distances = bellman_ford(start_node, edges, nodes)
if distances is not None:
print("Shortest distances from node A:")
for node in sorted(distances):
print(f"{node}: {distances[node]}")
# 예시 2: 음수 사이클이 있는 그래프
print("===================")
nodes = {"A", "B", "C"}
edges = [
("A", "B", 1),
("B", "C", -2),
("C", "A", -1)
]
distances = bellman_ford(start_node, edges, nodes)
if distances is not None:
print("Shortest distances from node A:")
for node in sorted(distances):
print(f"{node}: {distances[node]}")bellman_ford함수는 시작 노드, 간선 리스트, 노드 집합을 입력으로 받아 최단 거리를 반환합니다.V-1번 반복 이후에도 거리가 갱신되면 음수 사이클이 있다고 판단하여None을 반환합니다.
출력 결과 (Java, Python 동일)
===================
Shortest distances from node A:
A: 0
B: 4
C: 2
D: 5
===================
Graph contains a negative-weight cycle.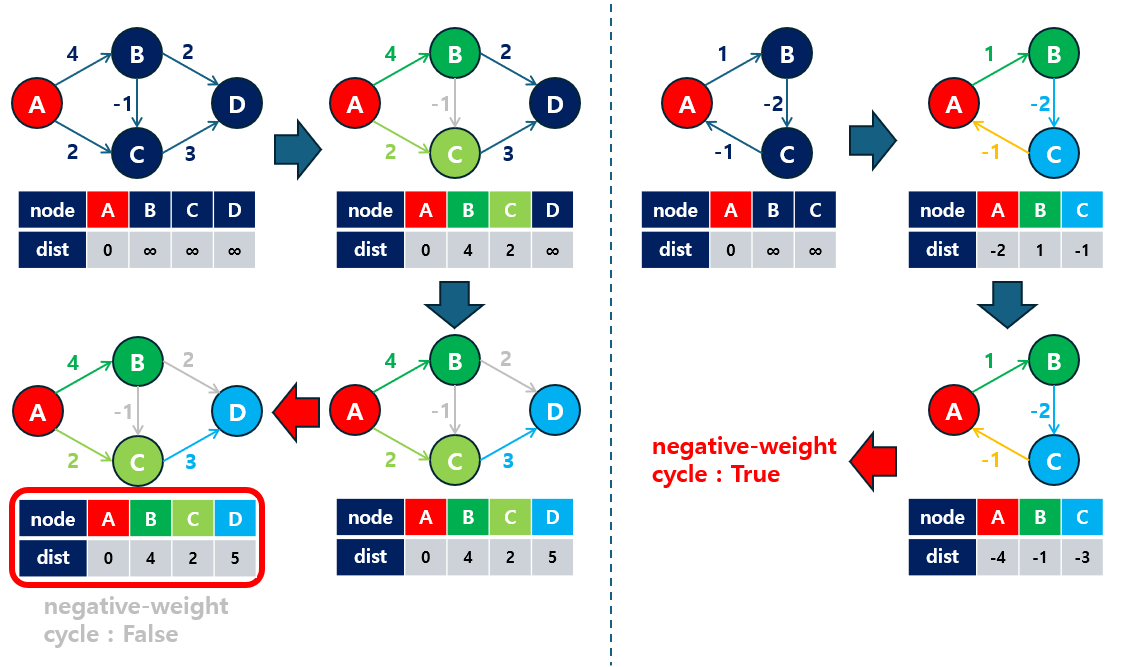
3-3. Floyd-Warshall Algorithm
플로이드-워셜(Floyd-Warshall) 알고리즘은 모든 정점 쌍 간의 최단 경로를 찾는 알고리즘입니다.
- 동적 계획법(Dynamic Programming)을 사용하여 모든 쌍에 대한 최단 경로를 효율적으로 계산합니다.
3-3.1 Floyd-Warshall 알고리즘 특징
- 적용 조건: 모든 쌍의 최단 경로를 구해야 하는 경우에 적합
- 가중치 조건: 양수 및 음수 가중치를 모두 처리 가능 (단, 음수 사이클이 있을 경우, 올바른 최단 경로를 구할 수 없음)
- 주요 사용 사례: 네트워크 최적화, 그래프 내 모든 노드 간의 최단 거리 계산, 사회적 거리 계산 등
- 시간 복잡도: , 여기서
V는 정점의 개수입니다.
플로이드-워셜 알고리즘은 모든 정점 간의 경로를 구해야 할 때 효율적이지만, 시간 복잡도가 높아 큰 그래프에는 적합하지 않습니다.
3-3.2 Floyd-Warshall 동작 원리
플로이드-워셜 알고리즘은 동적 계획법을 이용해 다음 원리에 따라 최단 경로를 갱신합니다.
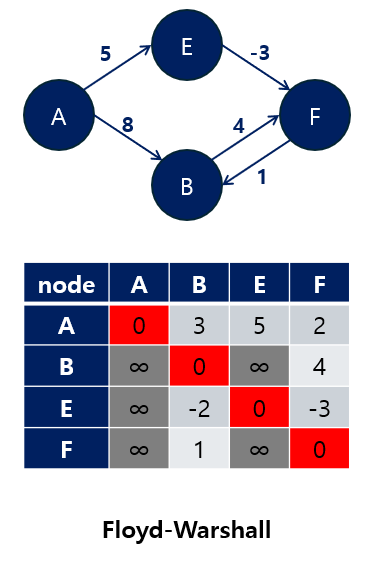
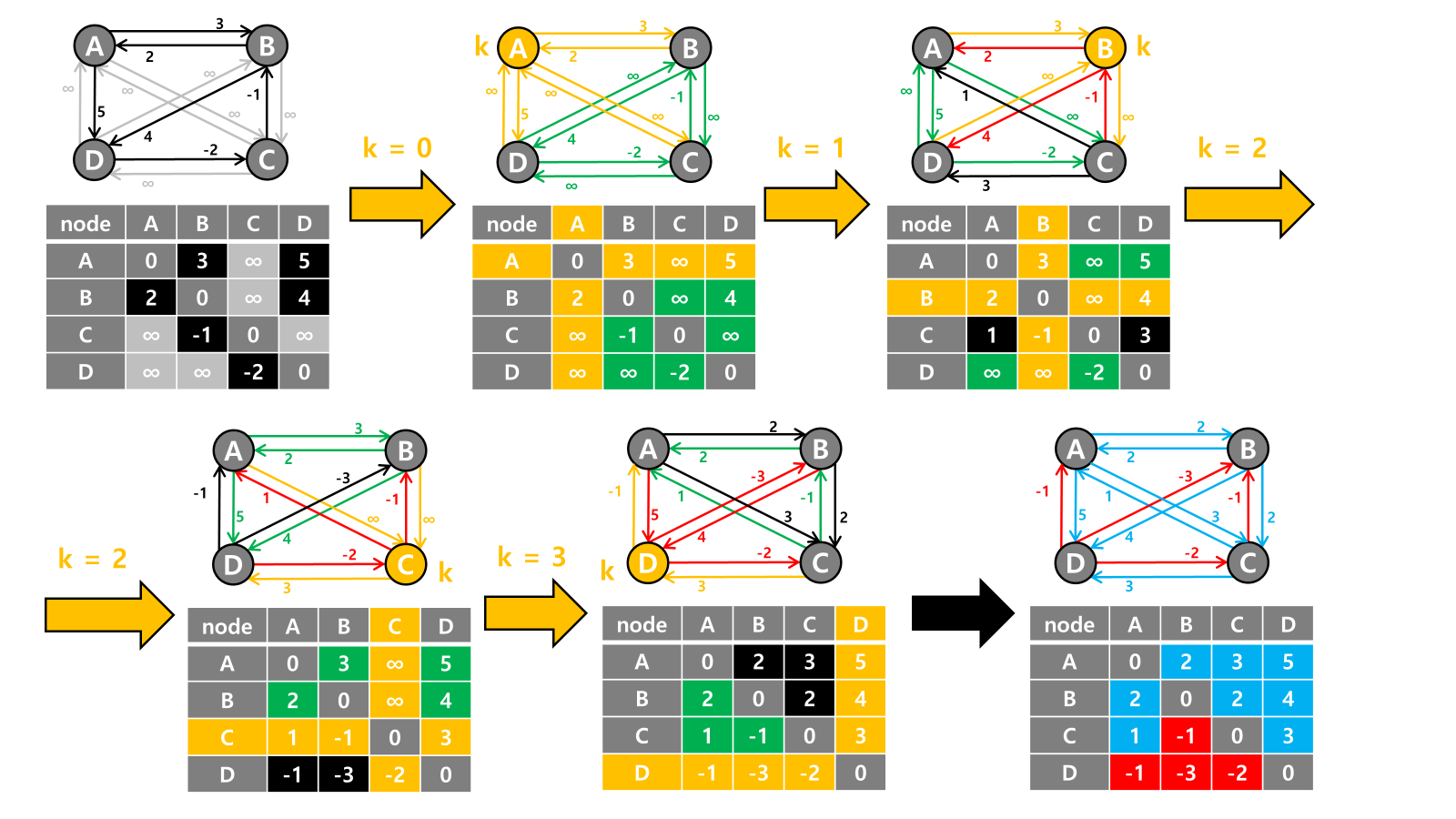
- 초기화: 각 정점 간의 거리를 인접 행렬로 표현하며, 자신에게 가는 거리는
0으로 설정하고 직접 연결되지 않은 노드 쌍은 무한대(혹은 MAX 값)로 설정합니다. - 경로 갱신: 모든 정점
k에 대해, 다른 모든 정점 쌍(i, j)의 경로를 확인합니다.i에서j로 가는 최단 경로가i → k → j를 거치는 것이 더 짧다면,(i, j)경로의 거리를 갱신합니다.
- 반복: 모든
k에 대해 위의 과정을 반복하여 최종적으로 각 정점 쌍 간의 최단 거리가 확정됩니다.
3-3.3 Floyd-Warshall 예제 코드 (Java & Python)
Java 예제 코드
public class FloydWarshallAlgorithm {
final static int INF = 99999; // 무한대 값
public static void floydWarshall(int[][] graph) {
int V = graph.length;
int[][] dist = new int[V][V];
// 초기화: 기존 그래프의 거리로 초기화
for (int i = 0; i < V; i++) {
System.arraycopy(graph[i], 0, dist[i], 0, V);
}
// 플로이드-워셜 알고리즘 수행
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][k] != INF && dist[k][j] != INF
&& dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// 최단 거리 출력
printSolution(dist);
}
public static void printSolution(int[][] dist) {
System.out.println("Shortest distances between every pair of vertices:");
for (int[] ints : dist) {
for (int anInt : ints) {
if (anInt == INF)
System.out.print("INF ");
else
System.out.print(anInt + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
// 예제 그래프 (인접 행렬 표현)
int[][] graph = {
{0 , 3 , INF, 5 },
{2 , 0 , INF, 4 },
{INF, -1 , 0 , INF},
{INF, INF, -2 , 0 }
};
floydWarshall(graph);
}
}floydWarshall메서드는 인접 행렬로 표현된 그래프를 받아 최단 거리 행렬을 출력합니다.INF값은 두 노드 간에 경로가 없음을 의미하며, 이를 통해 음수 사이클이 없는 모든 경로에 대해 최단 거리를 계산합니다.
Python 예제 코드
INF = float('inf') # 무한대 값
def floyd_warshall(graph):
v = len(graph)
dist = [row[:] for row in graph] # 그래프를 복사하여 거리 배열로 초기화
# 플로이드-워셜 알고리즘 수행
for k in range(v):
for i in range(v):
for j in range(v):
if dist[i][k] != INF and dist[k][j] != INF \
and dist[i][k] + dist[k][j] < dist[i][j]:
dist[i][j] = dist[i][k] + dist[k][j]
# 최단 거리 출력
print_solution(dist)
def print_solution(dist):
print("Shortest distances between every pair of vertices:")
for row in dist:
for val in row:
if val == INF:
print("INF", end=" ")
else:
print(f"{val:3}", end=" ")
print()
# 예제 그래프 (인접 행렬 표현)
graph = [
[ 0, 3, INF, 5],
[ 2, 0, INF, 4],
[INF, -1, 0, INF],
[INF, INF, -2, 0]
]
floyd_warshall(graph)floyd_warshall함수는 인접 행렬 형식의 그래프를 받아 최단 거리 행렬을 출력합니다.INF값은 경로가 없는 노드 쌍을 나타내며, 각 노드 쌍 간 최단 경로가 계산됩니다.
출력 결과 (Java, Python 동일)
Shortest distances between every pair of vertices:
0 2 3 5
2 0 2 4
1 -1 0 3
-1 -3 -2 0 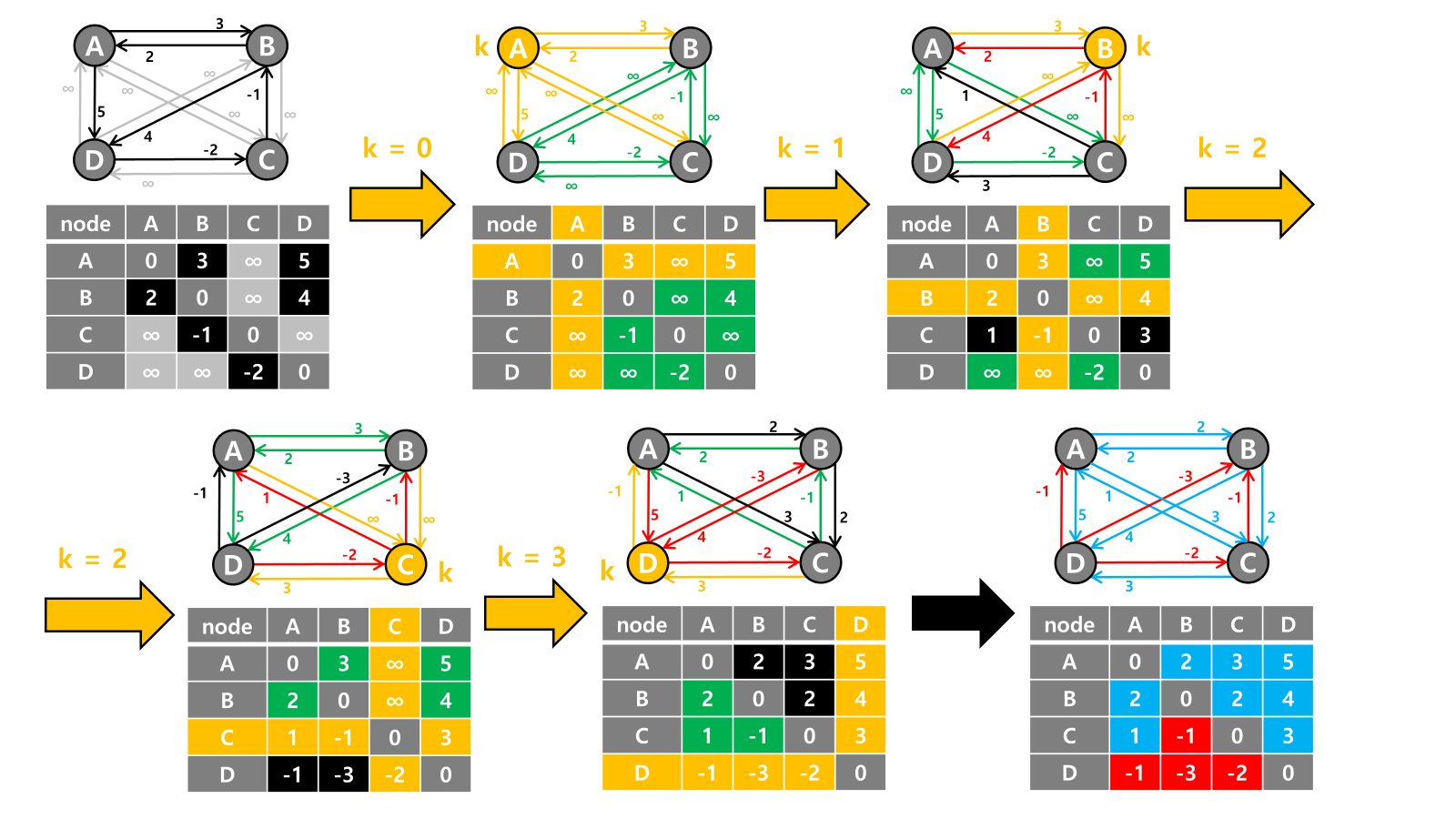
4. 최단 경로 알고리즘 비교
최단 경로 알고리즘들은 각각의 특성과 장단점이 다르기 때문에 다양한 상황에 맞게 선택하는 것이 중요합니다. 아래 표는 다익스트라(Dijkstra), 벨만-포드(Bellman-Ford), 플로이드-워셜(Floyd-Warshall) 알고리즘을 기준으로 각 알고리즘의 주요 특성과 적합한 상황을 비교한 것입니다.
| 알고리즘 | 적용 범위 | 가중치 조건 | 음수 가중치 | 음수 사이클 감지 | 시간 복잡도 | 주요 사용 사례 |
|---|---|---|---|---|---|---|
| 다익스트라 (Dijkstra) | 단일 시작점 | 양수만 가능 | 불가 | 불가 | 네비게이션 시스템, 지도 경로 찾기 | |
| 벨만-포드 (Bellman-Ford) | 단일 시작점 | 양수 및 음수 | 가능 | 가능 | 금융 거래, 주식 거래 차익 계산 | |
| 플로이드-워셜 (Floyd-Warshall) | 모든 쌍 | 양수 및 음수 | 가능 | 불가 | 네트워크 최적화, 모든 노드 간 거리 계산 |
알고리즘 선택 기준
- 다익스트라(Dijkstra) 알고리즘:
- 가중치가 양수이며, 단일 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 데 적합합니다.
- 시간 복잡도가 낮아 큰 그래프에서도 효율적입니다.
- 벨만-포드(Bellman-Ford) 알고리즘:
- 가중치에 음수가 포함되어 있을 경우 적합합니다.
- 또한, 음수 사이클을 감지할 수 있으므로 금융 네트워크처럼 손익을 계산하는 데 유용합니다.
- 다만, 시간 복잡도가 상대적으로 높습니다.
- 플로이드-워셜(Floyd-Warshall) 알고리즘:
- 모든 쌍의 최단 경로가 필요한 경우에 적합하며, 동적 계획법을 활용하여 효율적으로 모든 경로를 계산합니다.
- 그러나 시간 복잡도가 매우 높아 작은 그래프에 더 적합합니다.
마무리
이번 포스팅에서는 다익스트라(Dijkstra), 벨만-포드(Bellman-Ford), 플로이드-워셜(Floyd-Warshall) 알고리즘을 통해 최단 경로 문제를 해결하는 다양한 방법을 살펴보았습니다.
- 각 알고리즘은 그래프의 특성(가중치의 양수 여부, 모든 쌍의 경로 필요성 등)에 따라 사용 범위가 달라지며, 적용되는 상황에 따라 최적의 선택을 해야 합니다.
요약
- 다익스트라 알고리즘은 양수 가중치에서 단일 시작점의 최단 경로를 구하는 데 최적화되어 있습니다.
- 벨만-포드 알고리즘은 음수 가중치와 음수 사이클 감지가 필요할 때 유용하며, 상대적으로 높은 시간 복잡도를 가집니다.
- 플로이드-워셜 알고리즘은 모든 정점 쌍 간의 최단 경로를 계산해야 하는 경우 유용하며, 특히 작은 그래프에 적합합니다.
다음 포스팅에서는 최소 신장 트리(Minimum Spanning Tree)에 대해 다룰 예정입니다.
- 최소 신장 트리는 그래프의 모든 정점을 최소한의 간선 비용으로 연결하는 최적의 트리 구조를 찾는 문제로, 다양한 네트워크 최적화 문제에 적용할 수 있습니다.
- 크루스칼(Kruskal) 및 프림(Prim) 알고리즘을 통해 최소 신장 트리를 구하는 방법에 대해 알아보겠습니다.
