Computer 기초 - Bit & Logic Operation

1. Bit - 전기를 끄고, 킨다!

컴퓨터는 전기의 켜짐(1)과 꺼짐(0) 상태를 통해 모든 데이터를 처리하고 논리 연산을 수행합니다.

이를 통해 숫자와 문자 등의 데이터를 표현합니다.

• 문자: 첨자를 통해 크고(1) 작은(0) 원으로 표현
• 숫자: 2진법으로 0과 1로 표현
• 바코드: Bar와 Space로 0 또는 1을 표현

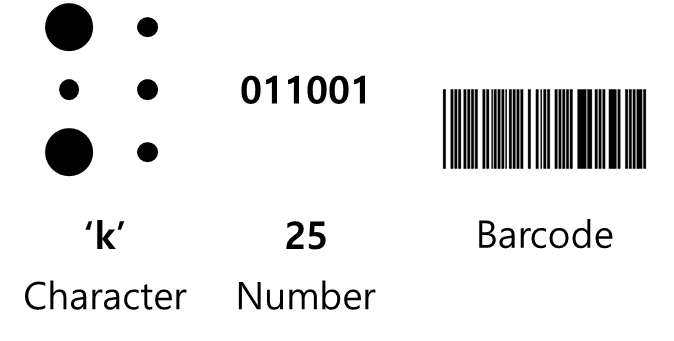
이 두 가지 상태만으로도 복잡한 연산과 처리가 가능하다는 것이 컴퓨터의 기본 원리입니다.

2. 논리 연산 (Logic Operation)

컴퓨터는 논리 게이트(Logic Gate)라는 기본 논리 연산을 통해 데이터를 처리하고 결정을 내립니다.

• 논리 연산은 주로 AND, OR, NOT, NAND, NOR, XOR와 같은 게이트로 이루어지며, 이러한 게이트는 0과 1, 즉 이진수 형태로 입력을 받아 특정 조건에 따라 출력을 만듭니다.

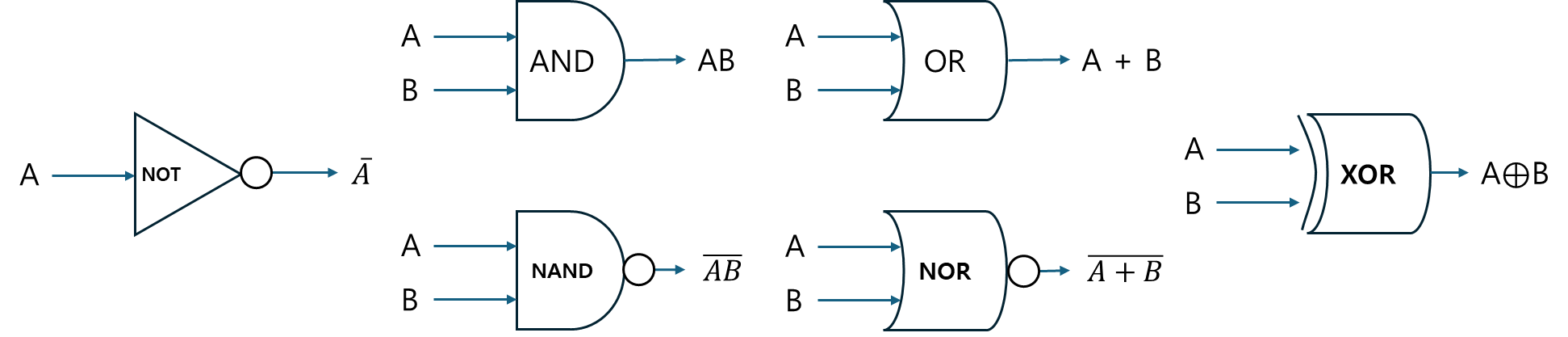
• NOT을 제외한 모든 기본 논리 연산은 2개의 Input과 1개의 Output으로 정의됩니다.

2.1 AND Gate

AND 게이트는 두 입력이 모두 1일 때만 출력이 1이 되는 논리 게이트입니다.

• 수학적으로는 $A ⋅ B$ 또는 $AB$ 로 표현합니다.

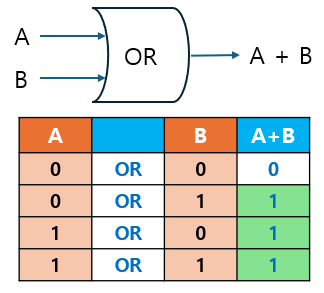
2.2 OR Gate

OR 게이트는 두 입력 중 하나라도 1이면 출력이 1이 되는 논리 게이트입니다.

• 수학적으로는 $A + B$ 로 표현합니다.

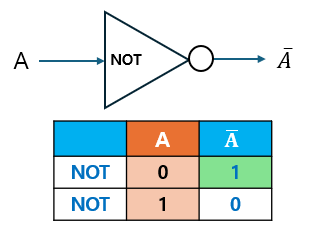
2.3 NOT Gate

NOT 게이트는 단일 입력을 받아 반전된 출력을 제공합니다.

• 입력이 A라면, 출력은 $A'$ 또는 $\overline{A}$ 로 표현됩니다.

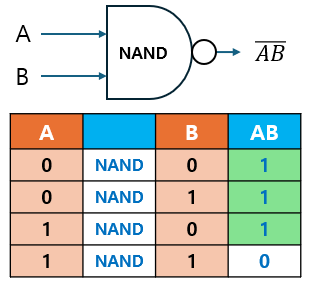
2.4 NAND Gate

NAND 게이트는 AND 게이트의 반전으로, 수학적으로는 $\overline{AB}$ 로 표현합니다.

• 이는 $A ⋅ B$의 출력 결과를 반전시킨 것입니다.

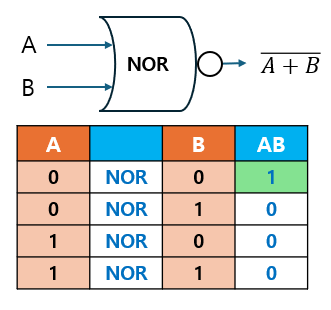
2.5 NOR Gate

NOR 게이트는 OR 게이트의 반전으로, 수학적으로는 $\overline{A+B}$ 로 표현합니다.

• 이는 $A + B$의 출력 결과를 반전시킨 것입니다.

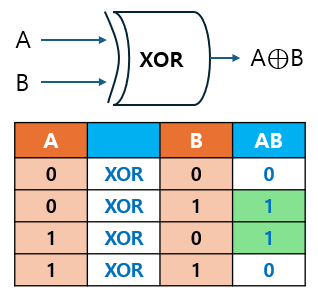
2.6 XOR Gate

XOR 게이트는 두 입력이 서로 다를 때 출력이 1이 되는 논리 게이트로, 수학적으로는 $A ⊕ B$로 표현합니다.

• XOR는 종종 배타적 논리합으로도 불리며, 두 신호가 다를 때만 참이 되는 연산입니다.

3. Boolean 연산과 게이트 요약

이제까지 살펴본 각 논리 게이트는 Boolean 연산으로 표현될 수 있으며, 컴퓨터 시스템의 기본적인 연산 원리를 형성합니다.

• Boolean 연산을 통해 컴퓨터는 0과 1로 이루어진 데이터를 처리하고 다양한 논리 연산을 수행할 수 있습니다.

다음은 주요 논리 게이트와 Boolean 표현식을 요약한 표입니다.

Gate	논리 설명	Boolean 표현식
AND	두 입력이 모두 1일 때만 출력이 1	$A \cdot B$ 또는 $AB$
OR	두 입력 중 하나라도 1이면 출력이 1	$A+B$
NOT	입력의 반전	$A'$ 또는 $\overline{A}$
NAND	AND의 반전	$\overline{AB}$
NOR	OR의 반전	$\overline{A+B}$
XOR	두 입력이 다를 때 출력이 1	$A ⊕ B$

Boolean 연산의 중요성

Boolean 연산은 논리 회로의 설계와 디지털 컴퓨팅의 핵심이 됩니다.

• 각 논리 게이트는 서로 다른 조건에 따라 데이터를 처리하고, 이를 결합하여 더욱 복잡한 회로와 연산을 구현할 수 있습니다.
• 예를 들어, 덧셈기나 곱셈기 같은 산술 회로는 기본적인 논리 게이트의 조합으로 만들어집니다.

논리 게이트의 조합

논리 게이트는 서로 조합하여 사용될 때 더욱 강력한 연산을 수행할 수 있습니다.

• 반가산기(Half Adder)는 XOR와 AND 게이트의 조합으로 두 비트의 덧셈을 수행합니다.
• 전체 가산기(Full Adder)는 반가산기와 AND, OR 게이트를 결합하여 세 비트를 덧셈할 수 있습니다.

반가산기와 전가산기는 다음 포스팅에서 자세히 다룹니다.

논리 게이트는 단순해 보일 수 있지만, 이러한 조합을 통해 복잡한 논리 연산과 데이터 처리가 가능합니다.

• 이는 컴퓨터가 연산, 제어, 데이터 저장을 효율적으로 수행할 수 있게 하는 기본 원리입니다.

마무리

이번 포스팅에서는 컴퓨터 시스템의 기본 연산 원리인 논리 게이트와 Boolean 연산에 대해 살펴보았습니다.

• 단순히 0과 1의 이진수만으로도 컴퓨터는 다양한 논리 연산을 수행할 수 있으며, 이를 통해 복잡한 데이터 처리와 연산을 가능하게 합니다.

특히, AND, OR, NOT, NAND, NOR, XOR와 같은 논리 게이트는 컴퓨터 회로 설계의 기초를 이루며, 이러한 게이트들의 조합을 통해 더 복잡한 논리 연산이 가능해집니다.

• 컴퓨터가 데이터를 받아들이고, 처리하고, 제어할 수 있는 것은 바로 이 논리 게이트들의 조합 덕분입니다.

다음 포스팅에서는 반가산기(Half Adder)와 전가산기(Full Adder)에 대해 다뤄보겠습니다. 이들은 두 개 또는 세 개의 비트를 더하는 회로로, 논리 게이트의 조합을 통해 만들어집니다.