
Computer 기초 - 가산기(adder)
1. 이진수의 덧셈과 Carry
- 컴퓨터는 이진수(0과 1)로 모든 연산을 수행합니다.
- 이진수의 덧셈에서는 자리 올림(Carry) 개념이 중요한 역할을 합니다.
Carry (자리 올림): 두 비트를 더할 때 자리수가 넘어가는 경우 추가되는 값
0 + 0 = 0(Carry 없음)0 + 1 = 1(Carry 없음)1 + 0 = 1(Carry 없음)1 + 1 = 0, Carry = 1
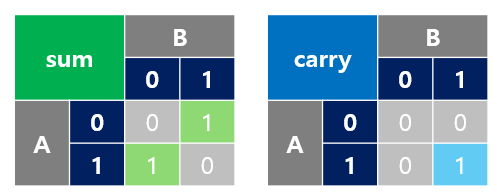
이진수 덧셈은 단순하지만, 자리 올림을 포함한 계산을 수행할 때는 가산기(adder)라는 논리 회로가 필요합니다.
2. XOR 게이트와 덧셈 연산
덧셈에서 XOR 게이트는 두 입력이 다를 때 1을 출력하는 성질을 활용해 합(sum) 계산에 사용됩니다.
OR와NAND게이트에AND게이트를 조합하면 XOR와 동일한 값을 얻을 수 있습니다.
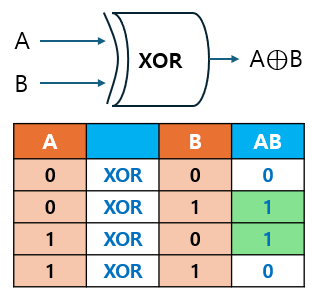
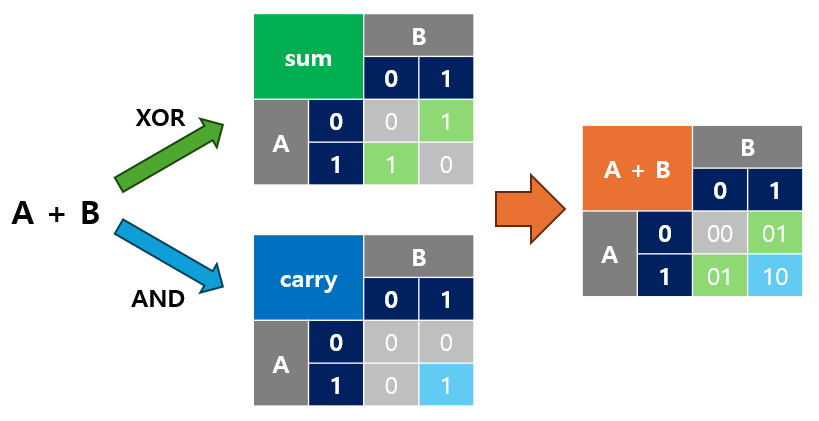
XOR 연산을 이용한 덧셈:
- 합(sum) : 입력
A와B를 XOR로 결합해 계산 가능 - 자리 올림(carry) : AND 게이트로 계산 가능
3. 반가산기 (Half Adder)
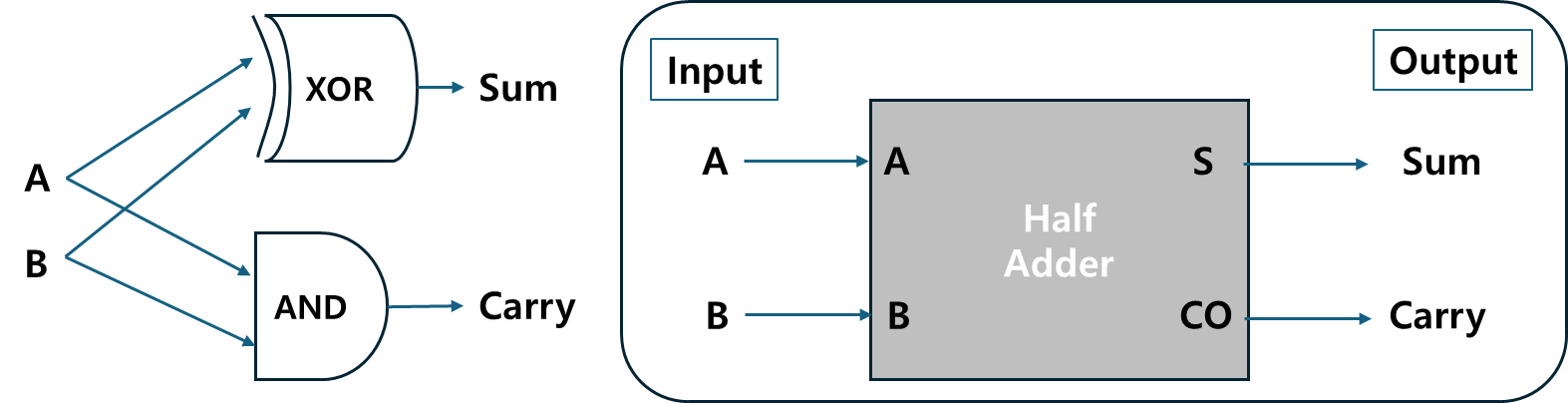
반가산기(Half Adder)는 두 개의 1비트 이진수를 더해 합(Sum)과 자리 올림(Carry)를 구할 수 있는 회로입니다.
- 반가산기는
A와B라는 두 입력을 받아Sum과Carry라는 두 출력을 반환합니다.- 합(sum) : (
XOR 게이트사용) - 자리 올림(carry) : (
AND 게이트사용)
- 합(sum) : (
| A | B | Sum (A ⊕ B) | Carry (A ⋅ B) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
반가산기는 간단한 덧셈을 수행할 수 있지만, 기존의 자리 올림(Carry In)을 입력으로 받지 못한다는 제한이 있습니다.
4. 전가산기 (Full Adder)
전가산기(Full Adder)는 반가산기를 확장하여 기존 자리 올림(Carry In)도 입력으로 받을 수 있는 회로입니다.
- 이를 통해 세 비트(A, B, Carry In)의 덧셈을 수행할 수 있습니다.
전가산기 출력:
- 합(Sum) :
- 자리올림(Carry Out) :
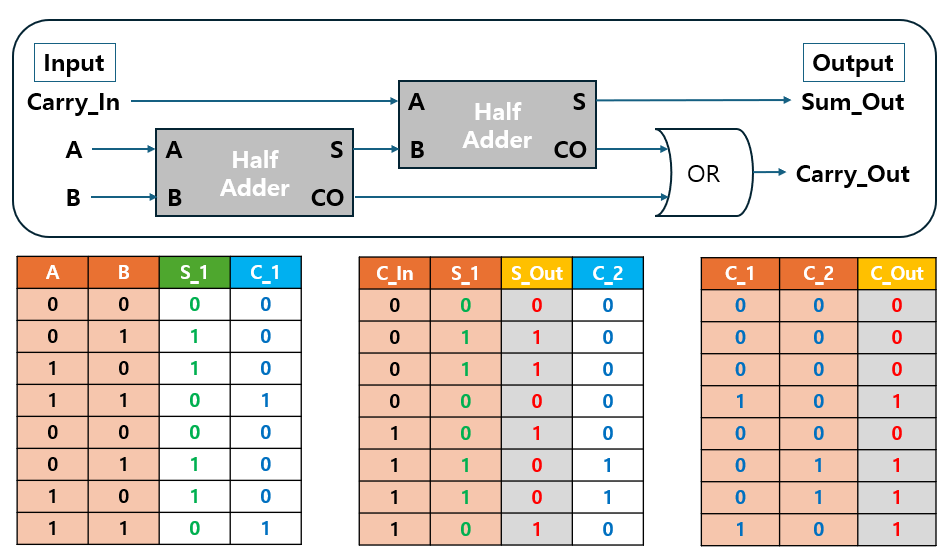
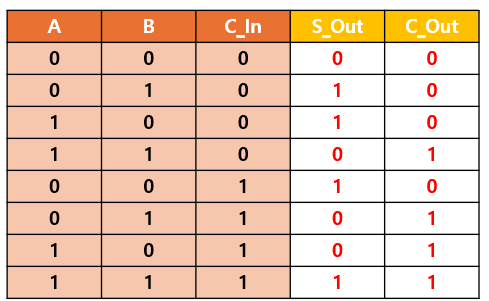
전가산기는 두 개의 반가산기를 조합하여 구현할 수 있습니다.
- 반가산기를 통해 간단한 덧셈을 수행한 뒤, 기존 자리 올림을 추가로 반영하는 방식입니다.
5. 다비트 전가산기 (Multi-Bit Adder)
다비트 전가산기는 여러 전가산기를 직렬로 연결하여 더 큰 수의 덧셈을 수행할 수 있는 구조입니다.
- 예를 들어, 8비트 전가산기나 16비트 전가산기는 각각
8비트또는16비트의 이진수를 더할 수 있습니다.
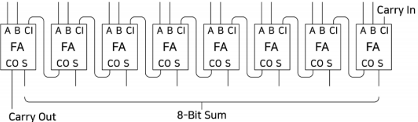
8비트 전가산기
- 8개의 전가산기를 직렬로 연결하여 8비트 이진수 덧셈을 수행합니다.
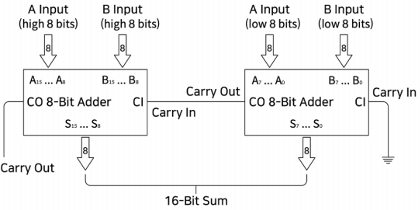
16비트 전가산기
- 16개의 전가산기를 연결하여 16비트 이진수 덧셈을 수행합니다.
- 실제로는 두 개의 8비트 전가산기가 병렬 연결된 형태입니다.
- 8비트는 시스템의 기본 단위인 1바이트에 해당하기 때문에, 이런 구조가 자주 사용됩니다.
결론적으로, 다비트 전가산기를 통해 더 큰 범위의 숫자를 처리할 수 있으며, 이는 컴퓨터의 정수 연산에서 중요한 역할을 합니다.
참고:
- Windows에서 흔히 쓰이는 32비트와 64비트 시스템은 각 연산에서 처리 가능한 데이터 크기와 메모리 주소 범위를 나타냅니다.
32비트 시스템은 최대4GB메모리까지만 처리할 수 있는 반면,64비트 시스템은 훨씬 더 큰 메모리를 처리할 수 있으며, 한 번에 더 많은 데이터를 연산할 수 있습니다.
마무리
이번 포스팅에서는 컴퓨터 연산의 기본 단위인 이진수 덧셈과 이를 구현하는 가산기(adder)의 원리에 대해 살펴보았습니다.
- 반가산기와 전가산기는 각각
1비트와여러 비트간의 덧셈을 수행할 수 있는 회로로, 컴퓨터가 숫자를 계산하는 기초 역할을 합니다. - 특히, 다비트 전가산기를 통해 더 큰 숫자를 처리할 수 있기 때문에 컴퓨터 시스템이 더 높은 범위의 정수를 연산할 수 있게 됩니다.
다음 포스팅에서는 CPU 클럭과 메모리 플립플롭에 대해 다룰 예정입니다.
- CPU의 속도를 결정하는 클럭과 데이터를 저장하는 메모리의 기본 단위인 플립플롭은 컴퓨터 성능과 메모리 구조를 이해하는 데 중요한 개념입니다.
