[자료구조] Linear Data - Stack (LIFO)

Kyung Jae, Cheong·2024년 10월 14일
Javapython자료구조
0

자료구조-DataStructure

목록 보기
4/19
post-thumbnail

본 시리즈는 프로그래밍 자료구조의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

  • 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
    • IDE : IntelliJ IDEA (Ultimate Edition)
    • Java : JDK 21 (corretto-21)
    • Python : 3.9 (conda env)

자료구조 - Stack

0. 서론: Stack이란?

스택(Stack)은 LIFO(Last In, First Out) 구조로 동작하는 선형 자료구조입니다.

  • 즉, 가장 마지막에 삽입된 데이터가 가장 먼저 삭제되는 구조입니다.

스택을 생각할 때는 흔히 접시를 쌓아 올리는 모습을 떠올리면 쉽습니다.

  • 새 접시는 맨 위에 놓고, 사용하려면 가장 위에 있는 접시를 꺼내는 것처럼 스택도 데이터를 추가할 때는 맨 위에 쌓고, 삭제할 때는 맨 위에서부터 제거합니다.
  • 즉, 데이터 삽입위치와 삭제위치가 같은 자료구조라고 생각하시면 됩니다.

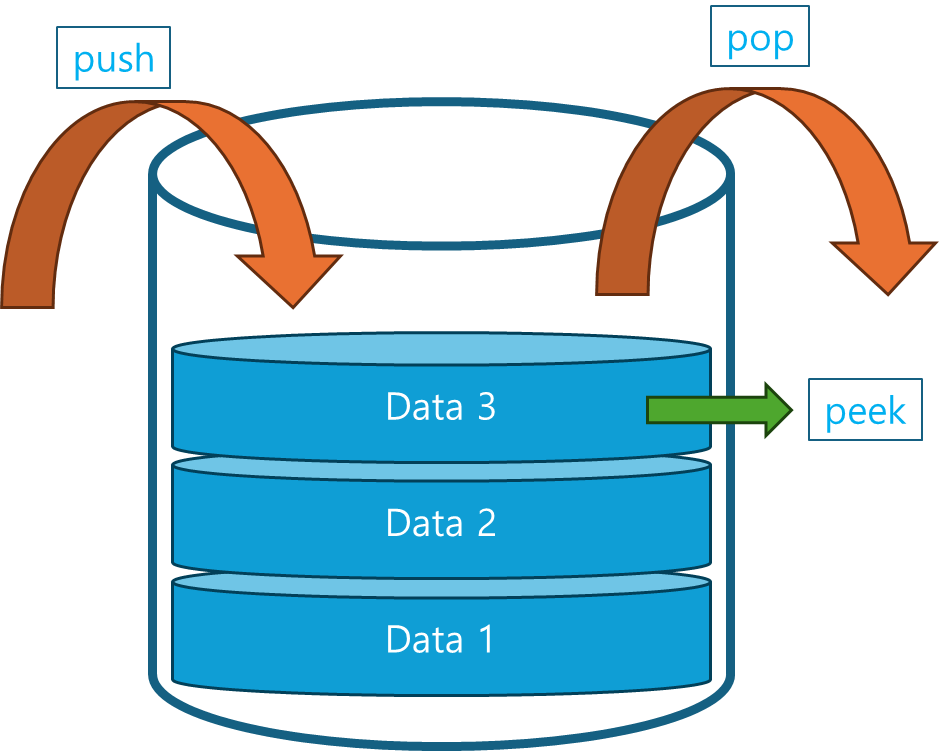
0.1 Stack의 주요 연산

스택에서는 주로 다음과 같은 연산으로 이루어집니다:

  • push: 스택의 맨 위에 데이터를 추가하는 연산.
  • pop: 스택의 맨 위 데이터를 제거하는 연산.
  • peek (또는 top): 스택의 맨 위에 있는 데이터를 제거하지 않고 확인하는 연산.
  • isEmpty: 스택이 비어 있는지 확인하는 연산.

0.2 Stack의 활용사례

스택은 여러 가지 상황에서 유용하게 활용됩니다. 대표적인 활용 사례로는 다음이 있습니다:

  • 함수 호출의 관리: 함수 호출이 일어날 때마다 해당 함수는 스택에 쌓이며, 함수가 종료될 때 스택에서 제거됩니다.
    • 이러한 방식으로 재귀 호출을 관리할 때도 스택이 사용됩니다.
    • 대부분의 프로그래밍 언어들은 이러한 Stack형태로 프로그램을 실행시키게 됩니다.
  • 문자열 또는 수식의 괄호 검사: 여는 괄호와 닫는 괄호의 짝을 맞추는 문제는 스택을 사용해 간단히 해결할 수 있습니다.
  • 뒤로 가기/앞으로 가기 기능: 웹 브라우저에서 뒤로 가기 버튼을 누르면 이전 페이지로 이동하는데, 이 역시 스택 구조를 사용하여 관리됩니다.
  • DFS (Depth First Search): 그래프 탐색에서 깊이 우선 탐색은 스택을 이용하여 탐색 순서를 관리합니다.

1. Stack 개념 및 구현

1.1 Java에서의 Stack

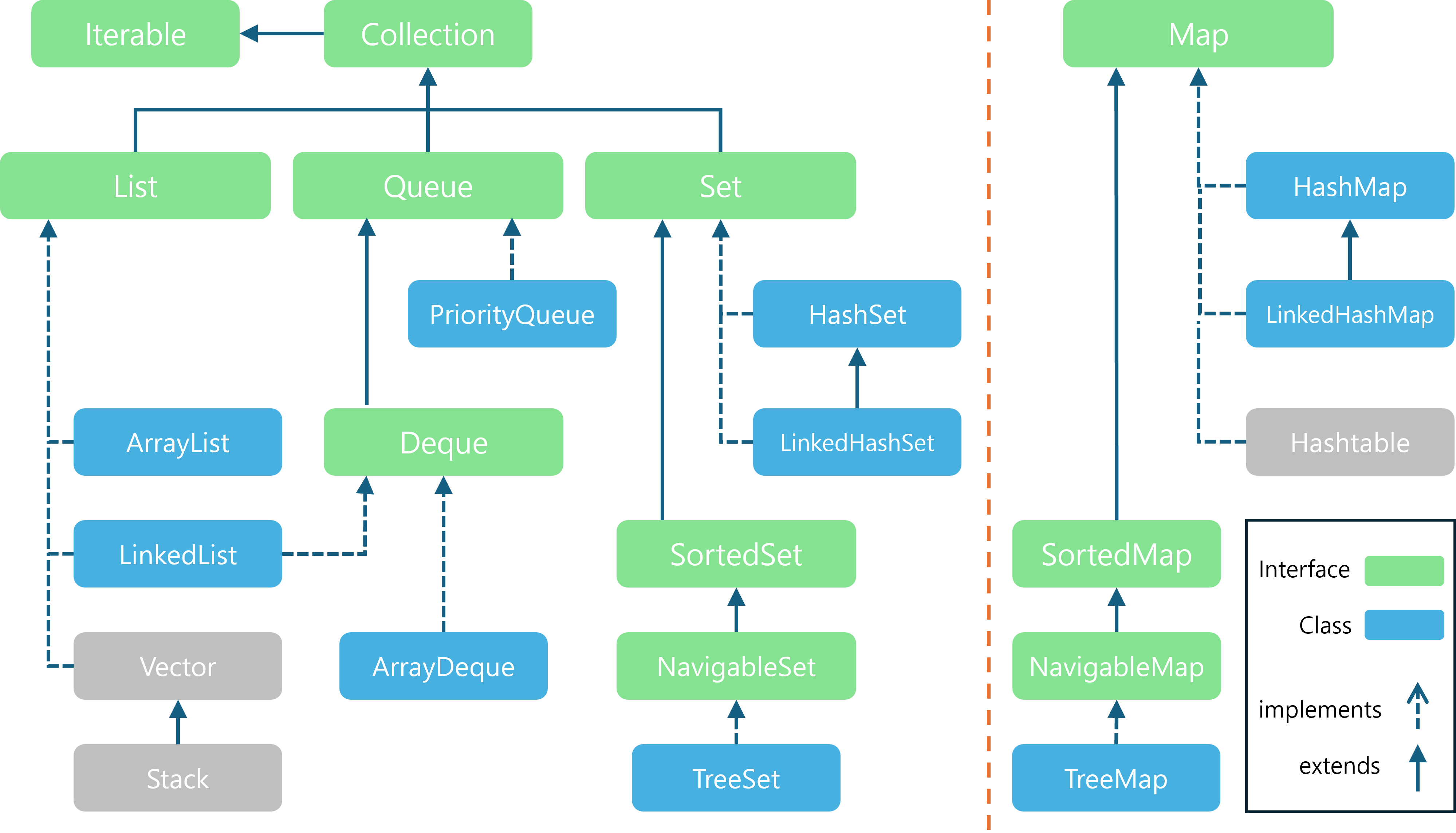
Java에는 Stack 클래스가 존재하고 기본적인 스택 연산인 push()와 pop()을 지원합니다.

  • 다만, Stack은 하위 버전 호환을 위한 Legacy 자료구조로 간주되며, 최신 Java에서는 Deque 인터페이스(ArrayDeque, LinkedList)를 사용하는 것이 더 권장됩니다.
  • Deque는 스택과 큐 양쪽에서 사용할 수 있는 자료구조로, 이후 포스팅에서 자세히 다루게 될 예정입니다.

Java Stack 클래스 사용 예시

import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        // Stack 생성
        Stack<Integer> stack = new Stack<>();

        // 데이터 추가 (Push)
        stack.push(10);
        stack.push(20);
        stack.push(30);

        // 데이터 제거 (Pop)
        System.out.println(stack.pop());  // 30 출력
        System.out.println(stack.pop());  // 20 출력

        // 현재 스택 상태
        System.out.println(stack);  // [10] 출력
    }
}

위 코드에서 push() 연산은 스택의 top(뒤쪽)에 데이터를 추가하고, pop() 연산은 top(뒤쪽)에서 데이터를 제거합니다.

  • 스택이 비어 있을 때 pop()을 호출하면 EmptyStackException이 발생합니다.

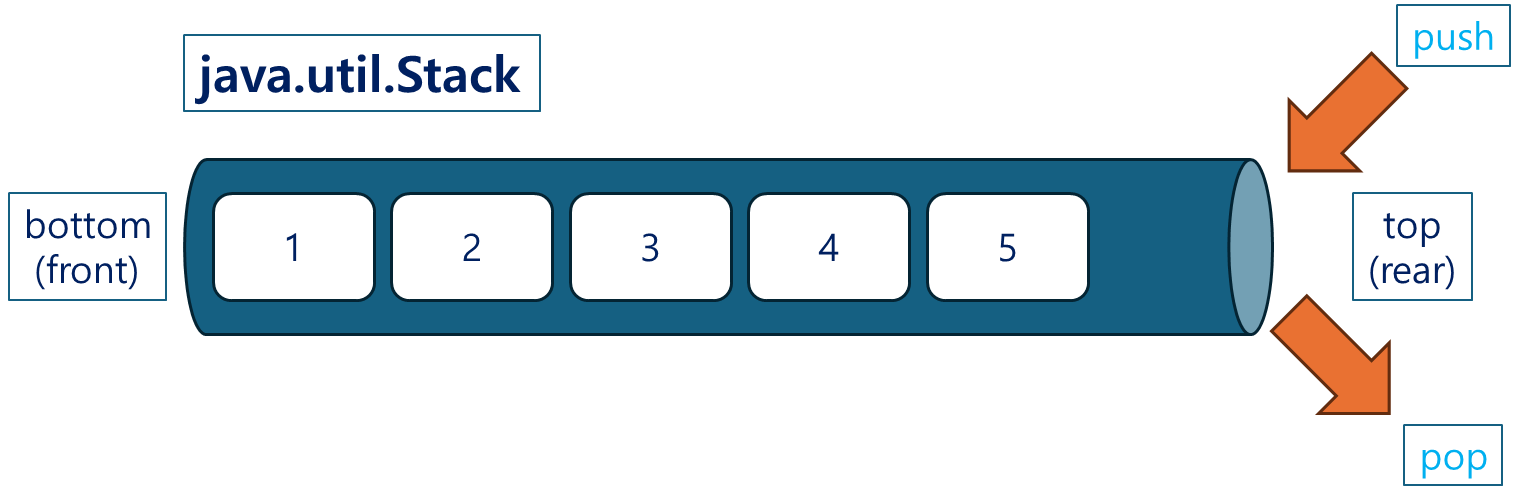
참고로 Java의 Stack 클래스는 LIFO (Last In, First Out) 원칙에 따라 동작하며, 자료구조의 뒤쪽에서 push와 pop 연산이 이루어집니다.

  • Java의 Stack은 내부적으로 List 인터페이스를 구현한 Vector를 상속받아 구현되었기 때문에, 데이터가 뒤쪽(리스트의 끝부분)에 쌓이고, push()와 pop() 모두 리스트의 끝에서 이루어집니다.

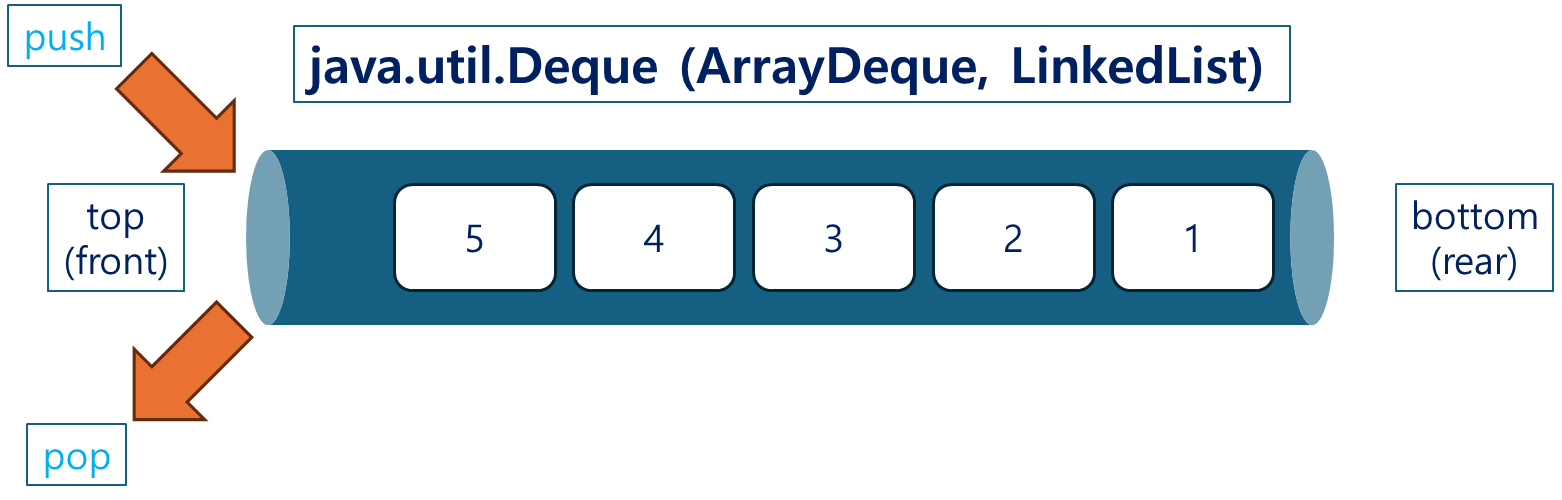
Deque 인터페이스 권장
Java에서 스택을 구현할 때는 Stack 클래스 대신 Deque 인터페이스를 구현한 ArrayDeque나 LinkedList로 스택을 구현하는 것이 더 권장됩니다.

  • Deque 구현체에서도 push()와 pop() 기능을 지원하기 때문에, Stack과 동일하게 사용하실 수 있습니다.
    • 다만, 이 경우엔 연산은 뒤쪽이 아닌 앞쪽에서 이루어집니다.
  • Deque는 더 다양한 기능을 제공하고, 성능적으로도 효율적입니다. 이 부분은 이후 포스팅에서 큐를 다룬 뒤에 더 자세히 다룰 예정입니다.

1.2 Python에서의 Stack

Python에서는 별도의 Stack 자료형이 존재하지 않지만, 두 가지 방법으로 스택을 구현할 수 있습니다:

  • 리스트(list)를 이용한 간단한 구현
  • collections.deque를 이용한 더 효율적인 구현

두 방법 모두 다루기는 하되, deque는 이후 포스팅에서 더 자세히 다룰 예정입니다.

리스트를 활용한 Stack 구현

Python의 리스트는 append()와 pop() 메서드를 통해 스택처럼 사용할 수 있습니다.

  • 리스트의 끝 부분을 스택의 top으로 간주하여 LIFO(Last In, First Out) 방식의 스택을 구현할 수 있습니다.
# Python 리스트를 이용한 스택 구현
stack = []

# 데이터 추가 (Push)
stack.append(10)
stack.append(20)
stack.append(30)

# 데이터 제거 (Pop)
print(stack.pop())  # 30 출력
print(stack.pop())  # 20 출력

# 현재 스택 상태
print(stack)  # [10] 출력

리스트는 스택처럼 작동하지만, 리스트의 pop() 연산은 마지막 요소에 대해서만 O(1) 시간 복잡도를 가지며, 중간에서 삭제하는 경우는 O(n)의 시간 복잡도가 발생할 수 있습니다.

  • 다만 Stack으로 사용하실땐 append()와 pop() 모두 O(1) 시간 복잡도를 가집니다.

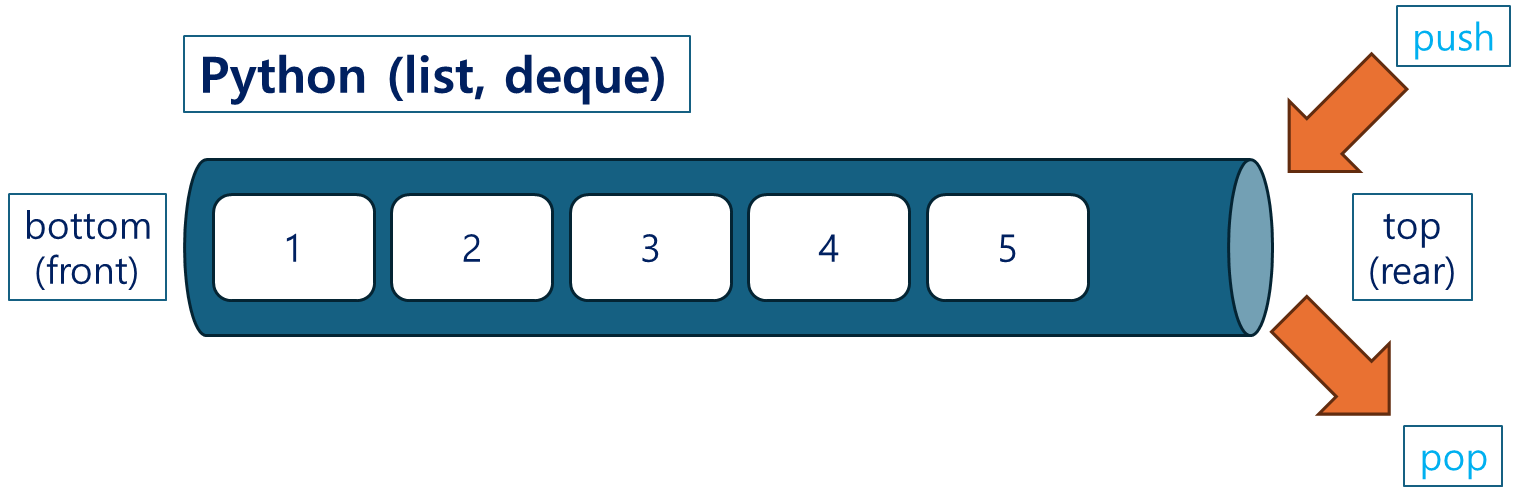
collections.deque를 이용한 Stack 구현

Python의 collections.deque는 스택과 큐 연산을 모두 효율적으로 처리할 수 있는 양방향 자료구조입니다.

  • 리스트보다 삽입과 삭제 연산이 더 효율적이며, 스택으로 사용하는 경우 O(1) 시간 복잡도를 보장합니다.
from collections import deque

# deque를 이용한 스택 구현
stack = deque()

# 데이터 추가 (Push)
stack.append(10)
stack.append(20)
stack.append(30)

# 데이터 제거 (Pop)
print(stack.pop())  # 30 출력
print(stack.pop())  # 20 출력

# 현재 스택 상태
print(stack)  # deque([10]) 출력

deque는 리스트보다 삽입 및 삭제가 훨씬 더 효율적인데, Deque의 더 다양한 기능과 활용법은 다음 포스팅에서 큐(Queue)와 함께 자세히 다룰 예정입니다.

1.3 스택의 구현 방법 비교

스택은 두 가지 주요 방식으로 구현될 수 있습니다: 배열 기반 스택과 연결 리스트 기반 스택.

  • 각각의 구현 방식은 고유한 장점과 단점을 가지고 있습니다.
구현 방식장점단점메모리 사용JavaPython
배열 기반
스택		- 메모리 연속성으로 인해
빠른 접근 속도
- 캐시 성능이 우수		크기 초과 시
배열 재할당으로 인한
비용 발생 가능		동적 크기 조절 가능
(재할당시 추가 메모리)		ArrayDequelist
연결 리스트
스택		- 동적 크기 조절이 가능
- 삽입/삭제가 배열보다 효율적		각 노드에 추가적인
메모리 사용 (포인터)		노드마다 추가적인
메모리 사용
(동적 메모리 할당)		LinkedListdeque
  • 배열 기반 스택 (ArrayDeque, list):
    • 크기가 꽉 찰 경우 내부적으로 배열의 크기를 확장하여 더 큰 배열로 데이터를 복사하는 방식으로 동작합니다.
    • 이때 추가적인 메모리 사용이 발생하지만, 크기를 초과하지 않는 한 삽입 및 삭제 연산은 빠르게 수행됩니다.
  • 연결 리스트 기반 스택 (LinkedList, deque):
    • 각 노드가 동적으로 할당되며, 필요에 따라 크기를 자유롭게 조정할 수 있습니다.
    • 하지만 각 노드에 추가적인 포인터 메모리(이전 노드와 다음 노드를 가리키는 포인터)가 필요하기 때문에 메모리 사용량이 더 큽니다.

2. Stack 활용 사례

스택은 다양한 문제에서 중요한 역할을 하는 자료구조입니다.

  • 스택을 활용한 대표적인 문제로는 괄호 검사 문제와 재귀 함수 변환이 있습니다.

2.1 괄호 검사 문제

스택을 이용하여 괄호의 짝이 올바른지 확인하는 문제는 전형적인 스택 활용 예시입니다.

  • 괄호의 열림과 닫힘을 처리하는데, 여는 괄호는 스택에 push하고, 닫는 괄호는 스택에서 pop하여 짝이 맞는지 확인합니다.
  • 만약 닫는 괄호가 나왔을 때 스택이 비어있거나, 짝이 맞지 않으면 올바르지 않은 괄호 배열임을 알 수 있습니다.

괄호 검사 문제 해결 방법

  1. 문자열을 차례대로 읽어갑니다.
  2. 여는 괄호는 스택에 푸시합니다.
  3. 닫는 괄호가 나오면 스택에서 가장 최근에 추가된 여는 괄호를 팝하여 짝이 맞는지 확인합니다.
  4. 문자열을 끝까지 처리한 후에도 스택이 비어 있지 않다면, 짝이 맞지 않는 괄호가 존재하는 것입니다.

Java 코드 예시

import java.util.Stack;

public class Main {
    public static boolean isValidParentheses(String s) {
        Stack<Character> stack = new Stack<>();
        for (char c : s.toCharArray()) {
            if (c == '(' || c == '{' || c == '[') {
                stack.push(c);  // 여는 괄호는 스택에 push
            } else {
                if (stack.isEmpty()) return false;  // 스택이 비어있으면 짝이 안맞음
                char open = stack.pop();  // 스택에서 여는 괄호를 pop
                if ((c == ')' && open != '(') 
                	|| (c == '}' && open != '{') 
                    || (c == ']' && open != '[')) {
                    return false;  // 짝이 맞지 않으면 false
                }
            }
        }
        return stack.isEmpty();  // 모든 처리가 끝난 후 스택이 비어있어야 true
    }

    public static void main(String[] args) {
        System.out.println(isValidParentheses("(){}[]"));  // true
        System.out.println(isValidParentheses("(]"));  // false
    }
}

Python 코드 예시

def is_valid_parentheses(s):
    stack = []
    matching_brackets = {')': '(', '}': '{', ']': '['}
    
    for char in s:
        if char in matching_brackets.values():
            stack.append(char)  # 여는 괄호 push
        elif char in matching_brackets.keys():
            if not stack or stack.pop() != matching_brackets[char]:  # 짝 확인
                return False
    return len(stack) == 0  # 스택이 비어 있어야 true

print(is_valid_parentheses("(){}[]"))  # True
print(is_valid_parentheses("(]"))  # False

2.2 Stack을 활용한 재귀함수 변환 (팩토리얼 예제)

스택은 재귀 함수의 호출을 반복문으로 변환할 때 사용할 수 있습니다.

  • 재귀 호출은 스택 메모리를 사용하기 때문에, 재귀를 반복문으로 변환할 때는 명시적인 스택 자료구조를 사용하여 호출 상태를 저장할 수 있습니다.

재귀 함수를 스택을 사용하여 반복문으로 변환하는 좋은 예로 팩토리얼 계산이 있습니다.

  • 팩토리얼은 자연수 n에 대해 n! = n * (n-1) * (n-2) * ... * 1로 정의됩니다.
  • 재귀적으로 팩토리얼을 구하는 코드가 더 간단하지만, 이를 스택을 사용하여 반복문으로 변환하는 방법도 가능함을 보여드리도록 하겠습니다.

1. 재귀 함수로 구현된 팩토리얼

우선, 재귀 함수를 사용하여 팩토리얼을 구현한 코드입니다:

  • Java
public class StackTest {

    // 재귀적으로 팩토리얼을 구하는 함수
    public static int recursiveFactorial(int n) {
        if (n == 0) {
            return 1;
        }
        return n * recursiveFactorial(n - 1);
    }

    public static void main(String[] args) {
        System.out.println(recursiveFactorial(5));  // 120 출력
    }
}
  • Python
# 재귀적으로 팩토리얼을 구하는 함수
def recursive_factorial(n):
    if n == 0:
        return 1
    return n * recursive_factorial(n - 1)

# 테스트
print(recursive_factorial(5))  # 120 출력

이 재귀 함수는 n == 0일 때 종료되며, n * recursiveFactorial(n - 1)을 반복적으로 호출하여 팩토리얼 값을 계산합니다.

2. 스택을 사용한 반복문으로 변환된 팩토리얼

이제 이 재귀 호출을 스택을 사용하여 반복문으로 변환해 보겠습니다.
스택을 사용하여 호출 스택을 모방하면, 명시적으로 함수 호출 상태를 저장하고 처리할 수 있습니다.

  • Java
import java.util.Stack;

public class StackTest {

    // 스택을 이용한 반복문으로 팩토리얼을 구하는 함수
    public static int stackFactorial(int n) {
        Stack<Integer> stack = new Stack<>();
        int result = 1;

        // n부터 1까지의 값을 스택에 넣습니다.
        while (n > 0) {
            stack.push(n);
            n--;
        }

        // 스택에서 값을 하나씩 꺼내어 팩토리얼을 계산합니다.
        while (!stack.isEmpty()) {
            result *= stack.pop();
        }

        return result;
    }

    public static void main(String[] args) {
        System.out.println(stackFactorial(5));  // 120 출력
    }
}
  • Python
# 스택을 이용한 반복문으로 팩토리얼을 구하는 함수
def stack_factorial(n):
    stack = []
    result = 1

    # n부터 1까지 스택에 값을 넣음
    while n > 0:
        stack.append(n)
        n -= 1

    # 스택에서 값을 꺼내어 팩토리얼 계산
    while stack:
        result *= stack.pop()

    return result

# 테스트
print(stack_factorial(5))  # 120 출력

위 예시 코드들은 다음과 같이 동작합니다.
1. 스택에 n부터 1까지의 값을 넣음: n이 0보다 큰 동안 스택에 값을 계속 추가합니다.
2. 스택에서 값을 하나씩 꺼내어 곱셈: 스택에서 값을 하나씩 꺼내면서 곱셈을 수행하여 팩토리얼을 계산합니다.

3. 재귀함수와 스택반복문 비교

  • 재귀적 함수는 함수가 반복적으로 호출되며, 함수 호출 스택을 사용해 값을 처리합니다.
  • 스택을 사용한 반복문은 명시적인 스택 자료구조를 사용하여, 함수 호출 없이도 값을 스택에 저장하고 처리합니다

3. Stack의 시간 및 공간 복잡도

스택(Stack)에서 이루어지는 연산들은 매우 효율적입니다.
스택에서 사용되는 대표적인 연산들의 시간 복잡도 및 공간 복잡도는 다음과 같습니다.

3.1 주요 연산의 시간 복잡도

  • push(): 스택의 맨 위에 새로운 데이터를 추가하는 연산입니다.
    • 스택의 크기에 관계없이 항상 시간 복잡도는 O(1)입니다.
  • pop(): 스택의 맨 위에서 데이터를 제거하는 연산입니다.
    • 마찬가지로 스택의 크기와 관계없이 맨 위 데이터를 제거하는 시간 복잡도는 O(1)입니다.
  • peek(): 스택의 맨 위 데이터를 제거하지 않고 확인하는 연산입니다.
    • 스택의 크기와 관계없이 맨 위 데이터를 조회하는 데 시간 복잡도는 O(1)입니다.
  • isEmpty(): 스택이 비어 있는지 여부를 확인하는 연산입니다.
    • 이는 내부적으로 스택의 크기 또는 상태만 확인하면 되므로 시간 복잡도는 O(1)입니다.

3.2 스택 전체 탐색의 시간 복잡도

스택에서의 탐색 연산은 스택의 모든 요소를 살펴보는 작업이므로, 최악의 경우 스택에 있는 모든 데이터를 확인해야 합니다.

  • 그래서 전체 탐색의 시간 복잡도는 O(n)입니다.
    • 여기서 n은 스택에 들어있는 데이터의 개수입니다.

따라서 스택은 다음과 같은 시간 복잡도를 가지고 있습니다:

연산시간 복잡도
push()O(1)
pop()O(1)
peek()O(1)
isEmpty()O(1)
전체 탐색O(n)

3.3 공간 복잡도

스택은 선형적인 공간 복잡도를 가집니다.

  • 스택에 들어가는 데이터의 개수가 늘어날수록, 필요한 메모리도 그에 비례하여 증가합니다.

공간 복잡도는 스택에 저장된 데이터의 개수에 따라 O(n)입니다.

  • 이는 특히 스택을 사용할 때 데이터가 계속 쌓여서 메모리를 많이 사용하게 될 가능성이 있는 재귀 호출에서 주의해야 합니다.
  • 스택을 너무 깊게 사용할 경우 스택 오버플로(Stack Overflow)가 발생할 수 있습니다.

스택 오버플로우 (Stack Overflow)란?

스택 오버플로우는 스택 메모리 영역이 가득 차서 더 이상 데이터를 저장할 수 없는 상태를 말합니다.

  • 이 현상은 주로 무한 재귀 호출이나 깊은 재귀 호출이 발생할 때 일어납니다.
  • 모든 함수 호출이 스택에 저장되므로, 재귀 호출이 너무 깊어지면 스택의 한계를 초과하여 오버플로우가 발생할 수 있습니다.

예를 들어, 다음과 같은 상황이 오버플로우를 일으킬 수 있습니다:

public class StackOverflowExample {
    public static void recursive() {
        recursive();  // 재귀 호출이 무한히 반복됨
    }

    public static void main(String[] args) {
        recursive();  // StackOverflowError 발생
    }
}

위와 같은 코드에서 함수가 무한히 호출되면 StackOverflowError가 발생합니다.

  • 스택 오버플로우를 방지하려면 재귀 깊이를 제한하거나 반복문으로 재귀를 변환하는 방법 등을 고려해야 합니다.

마무리

이번 포스팅에서는 스택(Stack) 자료구조의 개념, 구현 방법, 그리고 다양한 활용 사례를 살펴보았습니다.

  • 스택은 LIFO(Last In, First Out) 구조로 동작하며, 함수 호출 관리, 괄호 검사, 그리고 깊이 우선 탐색(DFS) 등에서 자주 사용되는 중요한 자료구조입니다.
  • 또한, 배열 기반 스택과 연결 리스트 기반 스택의 구현 방법을 비교해 보고, 각 방식의 장단점과 사용 사례에 대해서도 살펴보았습니다.
  • 재귀 함수의 반복문 변환에서도 스택을 직접 활용하는 방법을 실습했으며, 스택의 시간 복잡도와 스택 오버플로우(Stack Overflow)에 대한 개념도 이해하였습니다.

스택 자료구조는 매우 기본적이지만, 다양한 문제 해결에서 필수적인 역할을 하기 때문에 그 개념을 잘 이해하고 있는 것이 중요합니다.

다음 포스팅에서는 큐(Queue) 자료구조를 다룰 예정입니다.

  • 큐(Queue)는 FIFO(First In, First Out) 구조로 스택과는 반대되는 특징을 가진 선형 자료구조로, 다양한 대기열 관리나 BFS(너비 우선 탐색)에서 사용됩니다.

다다음 포스팅에선, 큐(Queue)와 스택(Stack)의 장점을 모두 갖춘 자료구조인 데크(Deque, Double-Ended Queue)를 살펴보며 큐와 스택을 더욱 효과적으로 다룰 수 있는 방법에 대해 논의할 예정입니다.

  • 스택에 대한 충분한 이해를 바탕으로 큐와 데크의 차이점과 활용 방법을 익히면, 효율적인 데이터 처리와 문제 해결에 중요한 기반을 마련할 수 있을 것입니다.
profile
Kyung Jae, Cheong
일 때문에 포스팅은 잠시 쉬어요 ㅠ 바쁘다 바빠 모두들 화이팅! // Machine Learning (AI) Engineer & BackEnd Engineer (Entry)
이전 포스트

[자료구조] Linear Data - Node 기반 LinkedList (단일 & 이중)

다음 포스트

[자료구조] Linear Data - Queue (FIFO)

0개의 댓글