본 시리즈는 프로그래밍 자료구조의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

• 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
  • IDE : IntelliJ IDEA (Ultimate Edition)
  • Java : JDK 21 (corretto-21)
  • Python : 3.9 (conda env)

비선형 자료구조 - Graph (Part 1)

1. Graph란?

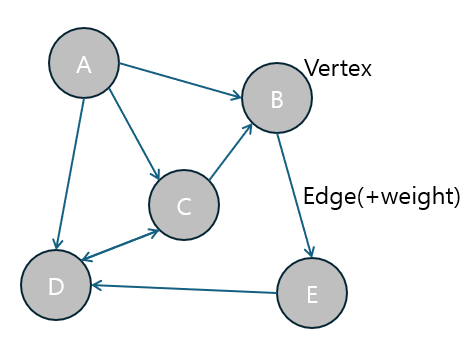
그래프(Graph)는 정점(Vertex)과 간선(Edge)으로 이루어진 비선형 자료구조입니다.

• 그래프는 다양한 데이터 관계를 모델링하는 데 사용되며, 현실 세계의 복잡한 상호작용을 표현하기에 매우 유용합니다.
• 다른 자료구조와 달리 비계층적이며, 정점 간의 다양한 연결을 표현할 수 있습니다.

1.1 그래프의 기본 구성 요소

• 정점(Vertex): 데이터를 저장하는 기본 단위입니다.
  • 보통 하나의 객체나 데이터를 나타내며, 이를 노드(Node)라고도 부릅니다.
• 간선(Edge): 두 정점 간의 관계를 나타내는 연결선입니다.
  • 간선은 두 정점을 연결하며, 이때 간선에는 방향이 있을 수도 있고, 없을 수도 있습니다.
• 가중치(Weight): 그래프에서 각 간선은 가중치를 가질 수 있습니다.
  • 가중치는 간선을 통해 이동하는 비용이나 거리 등을 나타내며, 이를 통해 최단 경로나 최소 비용 문제 등을 해결할 수 있습니다.

구성 요소에 대한 자세한 내용은 밑에서 다시 자세히 다룰 예정입니다 !

1.2 그래프의 주요 특징

• 비선형 자료구조: 그래프는 정점들이 서로 다양한 방식으로 연결될 수 있어, 단순히 순서가 있는 선형 자료구조와는 다릅니다.
• 유연한 구조: 정점이 어떻게 연결되든 다양한 형태를 가질 수 있으며, 현실 세계의 복잡한 상호작용을 효과적으로 모델링할 수 있습니다.
• 노드 간 관계 표현: 각 정점 간의 복잡한 관계를 표현하기 때문에, 트리 같은 자료구조보다 더욱 일반화된 데이터 모델입니다.
  • 트리는 그래프의 일종으로 계층을 가진 비선형 자료구조입니다. 다음 포스팅에서 다룰 예정입니다.

1.3 그래프의 주요 용도

그래프는 실생활의 여러 복잡한 시스템을 모델링할 때 사용됩니다. 예를 들어:

• 컴퓨터 네트워크: 컴퓨터(정점)들이 네트워크 연결(간선)을 통해 통신하는 방식.
• 소셜 네트워크: 사용자(정점)들이 친구나 팔로우 관계(간선)로 연결된 구조.
• 지도 및 길찾기: 장소(정점)들이 도로(간선)로 연결된 구조로, 이를 통해 최단 경로나 최소 비용 경로를 찾습니다.
• 웹페이지 링크 구조: 웹 페이지(정점)들이 하이퍼링크(간선)로 연결된 구조로, 검색 엔진에서 페이지의 중요도를 계산할 때 사용됩니다.

1.4 그래프의 실생활 예시

• 도로망: 도시나 교차로를 정점으로, 그 사이의 도로를 간선으로 표현한 지도.
• 항공편 경로: 공항을 정점으로 하고, 항공편을 간선으로 표현한 경로.
• 전력망 네트워크: 발전소나 전력소비처(정점)들이 전력선(간선)으로 연결된 구조.
• 추천 시스템: 사용자와 아이템을 정점으로, 구매하거나 선호하는 관계를 간선으로 표현한 추천 알고리즘의 기본 구조.

이처럼, 그래프는 현실 세계의 여러 복잡한 시스템을 데이터로 모델링하고 분석하는 데 유용합니다.

2. 그래프의 구성 요소 및 관련 용어

그래프는 현실 세계의 복잡한 관계를 모델링하는 데 매우 유용한 자료구조로, 기본적으로 정점(Vertex)과 간선(Edge)으로 이루어져 있습니다.

이 섹션에서는 그래프의 구성 요소와 함께, 관련 용어들을 자세히 설명합니다.

2.1 정점(Vertex)

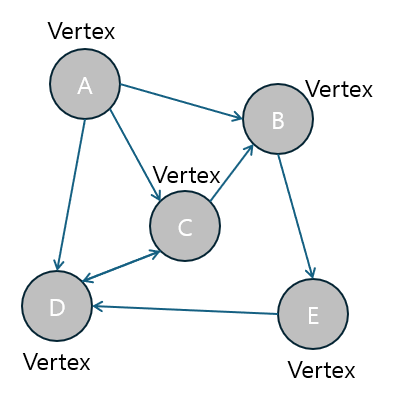
정점(Vertex)은 그래프의 기본 단위로, 데이터를 저장하는 역할을 합니다.

• 정점은 주로 Node(노드)라고도 불리며, 그래프에서 중요한 데이터가 저장되는 곳입니다.
• 정점들은 서로 간선으로 연결되어 있을 수도 있고, 연결되어 있지 않을 수도 있습니다.

예시:

• 소셜 네트워크에서는 각 사람이 정점으로 표현되며, 사람들 간의 관계가 간선으로 표현됩니다.
• 지도(Graph)에서는 각 도시나 교차로가 정점에 해당합니다.

2.2 간선(Edge, Link, Branch)

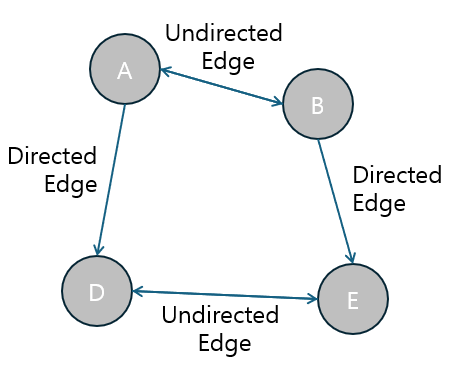
간선(Edge)은 두 정점을 연결하는 선으로, 두 정점 간의 관계나 연결을 나타냅니다. (Link, Branch, 등의 용어로도 불립니다)

• 간선에는 방향이 있을 수도 있고, 없을 수도 있습니다.
• 간선은 정점 간의 직접적인 경로를 나타내며, 그래프 구조에서 정점들의 연결성을 정의합니다.

간선의 유형:

• 유향 간선(Directed Edge): 간선이 한 방향으로만 연결되어 있는 경우, A에서 B로의 경로는 존재하지만 B에서 A로의 경로는 존재하지 않는 경우를 말합니다. (A -> B)
• 무향 간선(Undirected Edge): 양방향 연결을 의미하며, A에서 B로의 경로와 B에서 A로의 경로가 동일하게 존재합니다. (A <-> B 혹은 A - B)

예시:

• 항공편 경로에서 출발지와 도착지 간의 비행 경로는 유향 간선입니다.
• 도로망에서 쌍방향 도로는 무향 간선입니다.

2.3 가중치(Weight)

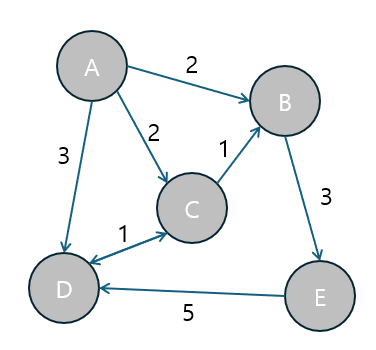
가중치(Weight)는 간선에 부여된 값으로, 거리, 비용, 시간 등의 개념을 표현할 때 사용됩니다.

• 가중치 그래프(Weighted Graph)는 각 간선에 가중치가 할당된 그래프입니다.
• 비가중치 그래프(Unweighted Graph)는 간선이 단순한 연결을 나타내며, 가중치가 없는 그래프입니다.

예시:

• 도로망에서 도로 간 거리를 나타내기 위해 간선에 거리 정보를 가중치로 할당할 수 있습니다.
• 네트워크 그래프에서 데이터 전송 비용을 나타내기 위해 간선에 전송 비용을 가중치로 사용할 수 있습니다.

2.4 차수(Degree)

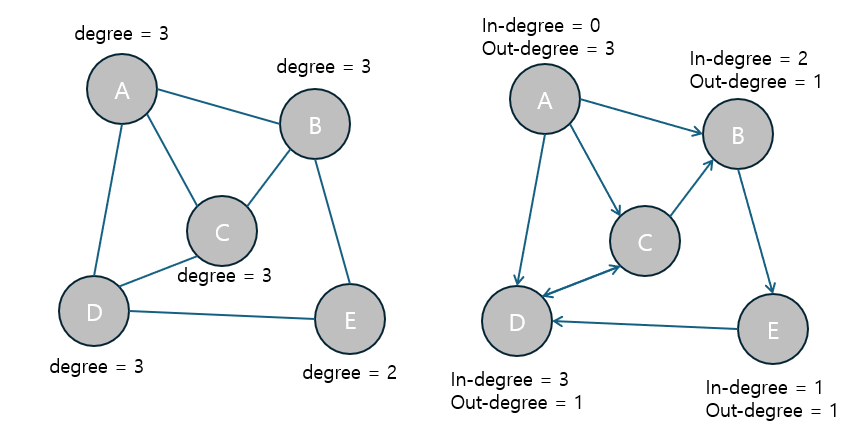
차수(Degree)는 한 정점에 연결된 간선의 개수를 의미합니다.

• 무향 그래프에서는 하나의 정점에 연결된 간선의 개수를 차수(Degree)라고 합니다.
• 유향 그래프에서는 진입 차수(In-degree)와 진출 차수(Out-degree)로 구분됩니다.
  • 진입 차수(In-degree): 외부에서 해당 정점으로 들어오는 간선의 수.
  • 진출 차수(Out-degree): 해당 정점에서 외부로 나가는 간선의 수.

예시:

• SNS에서 한 사용자가 팔로워와 팔로잉 관계를 맺는 경우, 진입 차수는 그 사용자를 팔로우하는 사람의 수를 나타내며, 진출 차수는 그 사용자가 팔로우하는 사람의 수를 나타냅니다.

2.5 경로(Path)

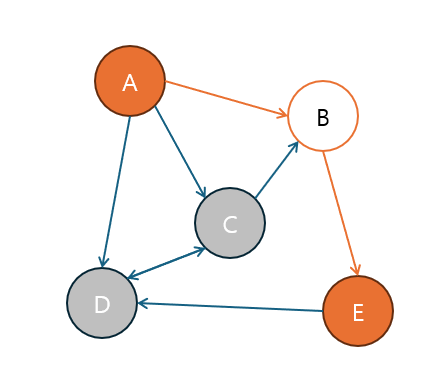
경로(Path)는 한 정점에서 시작하여 다른 정점으로 이동할 때 지나가는 정점들의 순서 또는 리스트입니다.

• 경로는 단순 경로(Simple Path)와 사이클(Cycle)로 나뉩니다.
  • 단순 경로(Simple Path): 동일한 정점을 두 번 이상 지나지 않는 경로.
  • 사이클(Cycle): 시작한 정점으로 다시 돌아오는 경로.
• 또한 이러한 경로의 길이를 경로 길이(Path Length)라고 합니다.
  • 그래서 최단경로(shortest path)는 가능한 모든 경로(Path)중 가장 짧은 경로 길이(Path Length)를 가지는 경로(Path)를 의미하게 됩니다.

예시:

• 도로망에서 한 도시에서 다른 도시로 이동하는 경로는 단순 경로일 수 있으며, 원래 도시로 돌아오는 경로는 사이클입니다.

2.6 연결성(Connectivity)

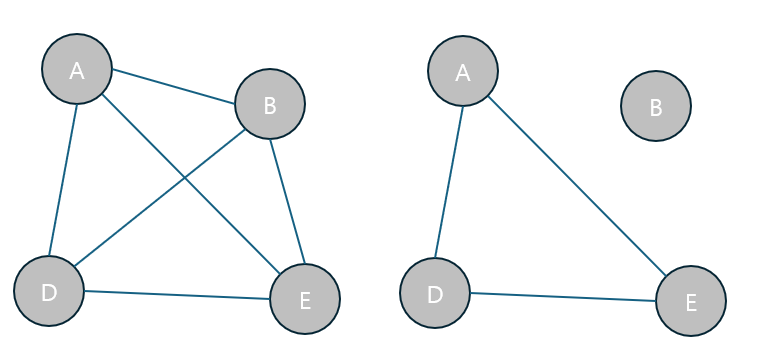
그래프에서 연결성(Connectivity)은 정점 간의 연결 여부를 나타냅니다.

• 연결 그래프(Connected Graph): 그래프 내의 모든 정점들이 직간접적으로 연결되어 있는 경우.
• 비연결 그래프(Disconnected Graph): 일부 정점들이 서로 연결되어 있지 않은 그래프.

예시:

인터넷 네트워크에서 모든 컴퓨터가 하나의 네트워크로 연결되어 있다면 연결 그래프이며, 네트워크에 연결되지 않은 컴퓨터가 있다면 비연결 그래프입니다.

2.7 인접(Adjacency)

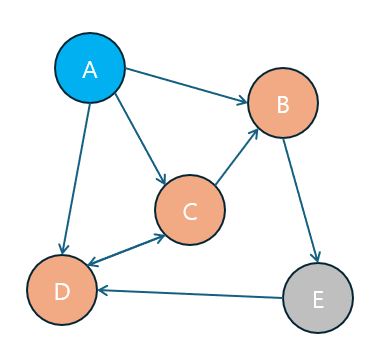
인접(Adjacency)는 두 정점이 간선으로 직접 연결되어 있는지 여부를 나타냅니다.

• 인접 정점(Adjacenct Vertex): 간선으로 직접 연결된 두 정점을 인접 정점이라 부릅니다.

예시:

• 그래프 탐색에서는 현재 정점과 인접한 정점을 탐색 대상으로 삼습니다.

3. 그래프의 종류

그래프는 구조와 속성에 따라 여러 가지로 분류될 수 있습니다. 이 섹션에서는 그래프의 다양한 종류를 정리합니다.

3.1 방향성에 따른 분류

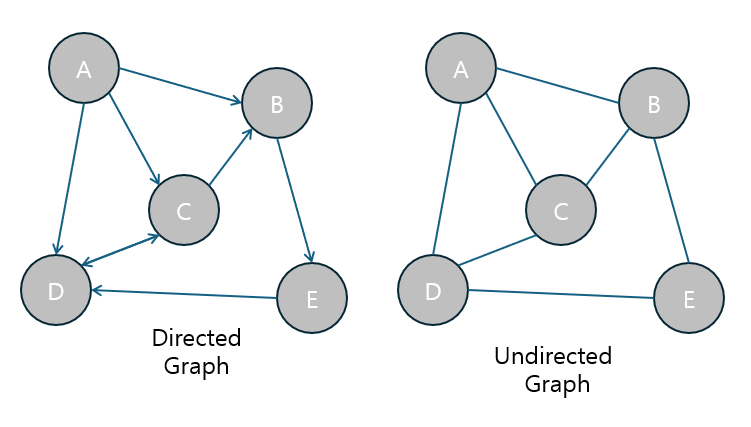
유향 그래프 (Directed Graph, Digraph)

유향 그래프는 간선에 방향이 있는 그래프입니다. (방향 그래프라고도 부릅니다)

• 각 간선은 특정한 방향으로 연결되며, 한 정점에서 다른 정점으로 한 방향으로만 이동할 수 있습니다.
  • 물론 일부 간선은 양방향으로 서로 연결될 순 있습니다. (다만 모든 간선이 양방향이면 유향 그래프로 분류하지 않습니다.)
• 예시: 소셜 네트워크에서 팔로우 관계 (A가 B를 팔로우한다고 해서 B가 A를 자동으로 팔로우하지 않음).
• 표기: 간선을 (A -> B)로 표시하거나 <A,B>로 표시하기도 합니다.

무향 그래프 (Undirected Graph)

무향 그래프는 간선에 방향이 없는 그래프입니다.

• 정점 간의 관계는 모두 양방향이며, 쌍방향 연결을 의미합니다.
  • 즉, A와 B가 서로 연결되어 있으면, 양쪽 방향 모두로 이동할 수 있습니다.
• 예시: 도로망에서 쌍방향 도로 (A에서 B로 가는 길이 있으면, B에서 A로 가는 길도 존재).
• 표기: 간선을 (A - B)로 표시하거나 (A,B)로 표시하기도 합니다.

3.2 가중치 여부에 따른 분류

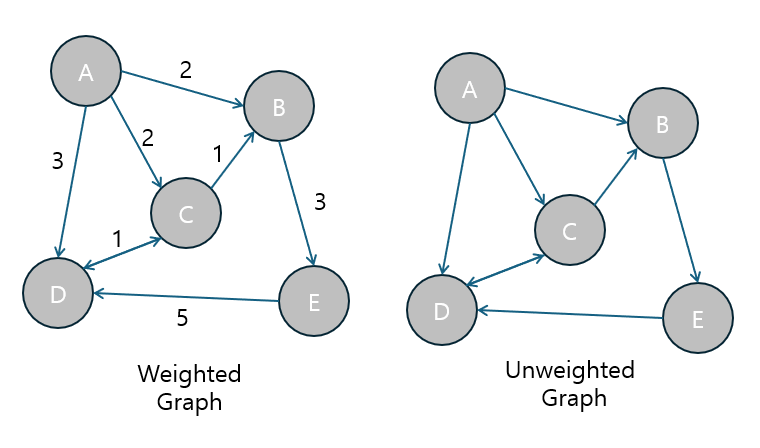
가중치 그래프 (Weighted Graph)

가중치 그래프는 각 간선에 가중치가 할당된 그래프입니다.

• 간선의 가중치는 거리, 비용, 시간 등을 나타내며, 최단 경로 문제나 최소 비용 문제를 해결할 때 주로 사용됩니다.
• 예시: 도로망에서 거리나 교통량을 가중치로 사용하는 그래프.
• 표기: 간선에 가중치를 적어서 표시합니다.
  • 예를 들어 (A - B, 3)은 A와 B 사이의 간선이 가중치 3을 가짐을 의미합니다.

비가중치 그래프 (Unweighted Graph)

비가중치 그래프는 간선에 가중치가 없는 그래프입니다.

• 간선이 단순히 연결 여부만을 나타내며, 각 연결의 중요도가 동일합니다.
• 예시: 소셜 네트워크에서 친구 관계는 간선에 가중치가 없는 경우가 많습니다.

3.3 연결 상태에 따른 분류

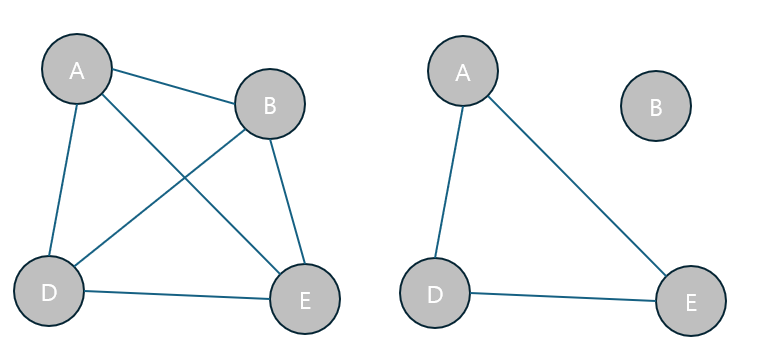
연결 그래프 (Connected Graph)

연결 그래프는 모든 정점이 서로 연결되어 있는 그래프입니다.

• 그래프 내의 어느 한 정점에서 다른 모든 정점으로 경로가 존재하는 경우를 말합니다.
• 예시: 완전한 컴퓨터 네트워크에서는 모든 컴퓨터가 연결되어 있어야 합니다.

비연결 그래프 (Disconnected Graph)

비연결 그래프는 일부 정점이 서로 연결되지 않은 그래프입니다.

• 일부 정점 간에는 경로가 존재하지 않으며, 여러 개의 독립된 하위 그래프들로 구성될 수 있습니다.
• 예시: 네트워크가 나뉘어 있는 경우.

3.4 순환 여부에 따른 분류

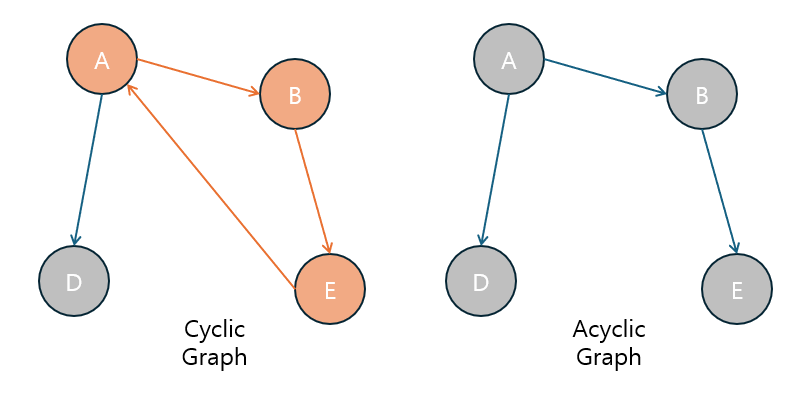
사이클 그래프 (Cyclic Graph)

사이클 그래프는 사이클(순환)이 존재하는 그래프입니다.

• 즉, 한 정점에서 시작해 여러 정점을 지나 다시 원래 정점으로 돌아오는 경로가 존재합니다.
• 예시: 도로망에서 다시 출발지로 돌아오는 경로가 존재하는 경우.

비순환 그래프 (Acyclic Graph)

비순환 그래프는 사이클이 없는 그래프입니다.

• 정점들 간에 순환 경로가 존재하지 않으며, 유향 비순환 그래프(DAG)는 정렬 문제나 작업 스케줄링 문제에서 자주 사용됩니다.
• 예시: 프로젝트의 작업 순서를 정하는 그래프.

3.5 상대적인 밀도에 따른 분류

희소 그래프 (Sparse Graph)

희소 그래프는 간선의 개수가 적은 그래프입니다.

• 정점에 비해 간선의 수가 상대적으로 적은 경우, 즉 m << n(n-1)/2인 경우입니다.
• 예시: 대규모 네트워크에서 일부 컴퓨터들만 연결된 상태.

밀집 그래프 (Dense Graph)

밀집 그래프는 간선의 개수가 많은 그래프입니다.

• 거의 모든 정점이 서로 연결되어 있는 그래프, 즉 m ≈ n(n-1)/2인 경우입니다.
• 예시: 모든 사용자들이 서로 연결된 소셜 네트워크.

3.6 특수한 형태의 그래프

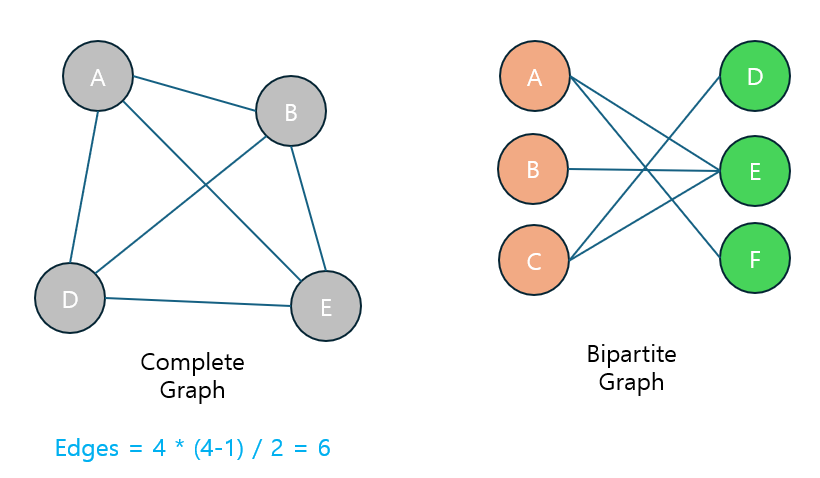
완전 그래프 (Complete Graph)

완전 그래프는 모든 정점이 서로 연결된 그래프입니다.

• n개의 정점이 있으면, 각 정점은 n-1개의 다른 정점과 연결됩니다.
  • 완전 그래프에서 간선의 개수는 n(n-1)/2입니다.
• 예시: 모든 도시가 도로로 직접 연결된 교통망.

이분 그래프 (Bipartite Graph)

이분 그래프는 두 개의 정점 집합으로 나눌 수 있으며, 한 집합의 정점은 다른 집합의 정점과만 연결되는 그래프입니다.

• 즉, 같은 집합 내의 정점들끼리는 연결되지 않고, 두 집합 간의 정점들만 간선으로 연결됩니다.
• 예시:
  • 구직자와 회사 간의 매칭 시스템 (구직자는 여러 회사에 지원하고, 회사는 여러 구직자를 채용할 수 있음).
  • 이진 매칭 문제나 헝가리안 알고리즘, 등

마무리

이번 포스팅에서는 그래프의 기본 개념과 그래프를 구성하는 요소들, 그리고 그래프의 다양한 분류에 대해 다뤘습니다.

• 정점(Vertex)과 간선(Edge)을 중심으로 그래프가 어떻게 현실의 복잡한 관계를 모델링할 수 있는지 이해하는 것이 중요한 첫걸음입니다.
• 그래프는 소셜 네트워크, 컴퓨터 네트워크, 지도, 추천 시스템 등 다양한 실생활 응용에서 사용되는 매우 강력한 자료구조입니다.

다음 포스팅에서는 프로그래밍 언어에서의 그래프 표현 방법과 구현 방법에 대해 더 깊이 다루고, 그래프를 활용하는 알고리즘 예시들을 간단하게 소개하는 시간을 가져보려합니다. (알고리즘의 구체적인 내용들은 알고리즘 파트에서 따로 다룹니다)