
본 시리즈는 프로그래밍 자료구조의 개념을 정리하고 실습을 진행해보는 시리즈입니다.
- 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
- IDE : IntelliJ IDEA (Ultimate Edition)
- Java : JDK 21 (corretto-21)
- Python : 3.9 (conda env)
트리(Tree) - AVL Tree
- 일반적인 Tree에 대한 전반적인 내용들은 다음 포스팅에서 확인하실 수 있습니다.
- 이진트리에 대한 기본적인 내용들은 다음 포스팅에서 확인하실 수 있습니다.
- 이진탐색트리(BST)에 대한 전반적인 내용들은 다음 포스팅에서 확인하실 수 있습니다.
1. AVL Tree란?
발명자의 이름인 Adelson-Velsky and Landis에서 따온 이름입니다.
AVL Tree는 균형 이진 탐색 트리(Self-balancing Binary Search Tree)의 일종으로, 트리의 높이를 항상 일정하게 유지하여 탐색, 삽입, 삭제 연산에서 O(log n)의 성능을 보장하는 자료구조입니다.
AVL 트리는 삽입이나 삭제가 발생할 때마다 트리의 균형을 유지하기 위해 회전(Rotation) 연산을 사용합니다. 이러한 균형 유지 메커니즘 덕분에, 비균형 트리로 인한 성능 저하를 방지할 수 있습니다.
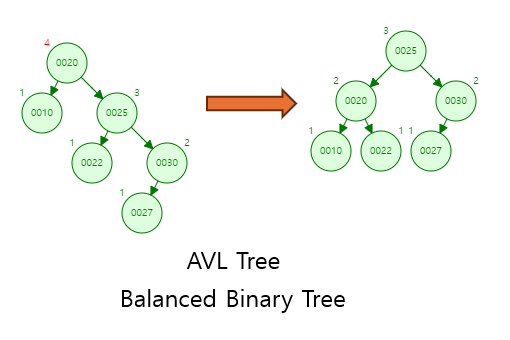
1.1 AVL Tree의 주요 특징
-
균형 인수(Height Balance Factor):
- AVL 트리에서는 각 노드에 대해 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 균형 인수라고 합니다.
- 균형 인수는
-1,0,1을 유지해야 합니다.0: 왼쪽과 오른쪽 서브트리의 높이가 동일함.1: 왼쪽 서브트리의 높이가 오른쪽보다 1 크다는 의미.-1: 오른쪽 서브트리의 높이가 왼쪽보다 1 크다는 의미.
- 쉽게 생각하면
왼쪽 높이 - 오른쪽 높이입니다.
-
균형을 깨트리는 연산:
- 삽입 또는 삭제 시, 특정 노드에서 균형 인수가 2 이상이 되면 트리의 균형이 깨진 것입니다.
- 이 경우 회전 연산(Rotation)을 통해 트리의 균형을 유지합니다.
-
회전 연산:
- 트리가 균형을 유지하지 못할 때, 회전 연산을 통해 균형을 되찾습니다.
- AVL 트리의 회전 연산은 단순 회전(Single Rotation)과 이중 회전(Double Rotation)으로 나뉩니다.
- 단순 회전(Single Rotation): 트리가 한쪽 방향으로만 치우친 경우 사용.
LL회전,RR회전
- 이중 회전(Double Rotation): 두 방향으로 치우친 경우 사용.
LR회전,RL회전
- 단순 회전(Single Rotation): 트리가 한쪽 방향으로만 치우친 경우 사용.
-
시간 복잡도:
- 탐색, 삽입, 삭제 연산 모두에서 O(log n)의 성능을 보장합니다.
- 회전 연산이 추가되지만, 트리의 높이를 일정하게 유지하므로 전체적인 성능은 여전히 뛰어납니다.
1.2 AVL Tree의 장단점과 주요 용도
장점:
- O(log n)의 성능 보장: 균형을 유지하기 때문에 최악의 경우에도 탐색, 삽입, 삭제 연산이 항상 O(log n)에 이루어집니다.
- 트리의 균형 유지: 비균형 상태로 인해 성능이 저하되는 상황을 방지할 수 있습니다.
- 확실한 균형: AVL 트리는 회전 연산을 통해 항상 트리의 균형을 엄격하게 유지합니다.
단점:
- 복잡한 삽입과 삭제: 균형을 맞추기 위한 회전 연산이 추가되면서 삽입과 삭제 시 일반적인 이진 탐색 트리보다 연산량이 늘어납니다.
- 높은 유지비용: 트리의 균형을 유지하기 위한 회전 연산은 성능이 조금 더 요구될 수 있어, 삽입/삭제가 빈번한 환경에서는 오히려 부담이 될 수 있습니다.
주요 용도:
- 동적 데이터 관리: AVL 트리는 삽입, 삭제가 빈번한 데이터 구조에서 성능 저하 없이 데이터를 효율적으로 관리하는 데 적합합니다.
- 탐색 중심 시스템: AVL 트리는 탐색 연산이 많은 시스템에 적합하며, 특히 검색 엔진, 데이터베이스 등에서 사용됩니다.
- 정렬된 데이터 유지: 중위 순회를 통해 데이터를 항상 정렬된 상태로 유지할 수 있어, 실시간 정렬이 필요한 시스템에서 유용합니다.
2. AVL Tree의 동작 원리
AVL 트리는 삽입(Insertion), 삭제(Deletion) 시 트리의 균형을 유지하기 위해 회전 연산을 사용합니다. 이 섹션에서는 트리의 균형이 깨졌을 때 회전으로 균형을 되찾는 과정을 설명합니다.
2.1 트리의 균형이 깨지는 경우
AVL 트리에서 노드를 삽입하거나 삭제할 때, 특정 노드의 균형 인수(Balance Factor)가 2 이상 또는 -2 이하로 변할 수 있습니다.
- 이때 트리는 불균형 상태가 되어, 회전 연산을 통해 균형을 맞춰야 합니다.
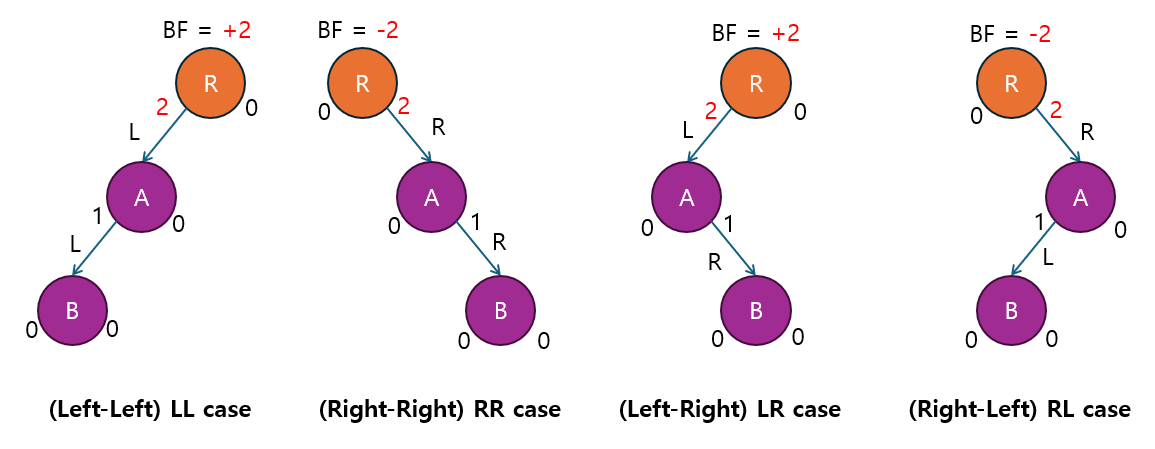
트리의 균형이 깨질 때는 네 가지 케이스가 발생합니다:
- LL 케이스 (Left-Left): 트리의 왼쪽 자식 노드가 다시 왼쪽 자식 노드를 가지고 있는 경우.
- 참고로 왼쪽 자식의 BF가 0이어도 LL 케이스에 해당합니다.
- 즉, 왼쪽 자식의 BF가 0보다 크거나 같은 경우입니다.
- RR 케이스 (Right-Right): 트리의 오른쪽 자식 노드가 다시 오른쪽 자식 노드를 가지고 있는 경우.
- 참고로 오른쪽 자식의 BF가 0이어도 RR 케이스에 해당합니다.
- 즉, 오른쪽 자식의 BF가 0보다 작거나 같은 경우입니다.
- LR 케이스 (Left-Right): 트리의 왼쪽 자식 노드가 오른쪽 자식 노드를 가지고 있는 경우.
- 즉, 왼쪽 자식의 BF가 0보다 작은 경우입니다.
- RL 케이스 (Right-Left): 트리의 오른쪽 자식 노드가 왼쪽 자식 노드를 가지고 있는 경우.
- 즉, 오른쪽 자식의 BF가 0보다 큰 경우입니다.
각 케이스에 맞는 회전 연산을 적용하여 트리의 균형을 맞출 수 있습니다.
- 트리가 불균형 상태에 있을 때, 이를 해결하기 위해 단일 회전(Single Rotation) 또는 이중 회전(Double Rotation)이 사용됩니다.
다음과 같이 각 회전 케이스를 표로 정리할 수 있습니다:
| 회전 종류 | 조건 (루트 노드의 BF) | 자식 노드의 BF 조건 | 설명 |
|---|---|---|---|
| LL 회전 | BF ≥ +2 | 왼쪽 자식의 BF ≥ 0 | 왼쪽 자식이 다시 왼쪽으로 치우친 경우. 단순 LL 회전으로 해결. |
| RR 회전 | BF ≤ -2 | 오른쪽 자식의 BF ≤ 0 | 오른쪽 자식이 다시 오른쪽으로 치우친 경우. 단순 RR 회전으로 해결. |
| LR 회전 | BF ≥ +2 | 왼쪽 자식의 BF < 0 | 왼쪽 자식이 오른쪽으로 치우친 경우. 먼저 RR 회전 후, LL 회전. |
| RL 회전 | BF ≤ -2 | 오른쪽 자식의 BF > 0 | 오른쪽 자식이 왼쪽으로 치우친 경우. 먼저 LL 회전 후, RR 회전. |
2.2 회전 연산 (Rotation) - 단일 회전 (Single Rotation)
2.2.1 LL 회전 (Left-Left 회전)
- 왼쪽 자식이 왼쪽 서브트리를 가지는 LL 케이스 (Left-Left)에서 불균형을 해결하는 회전입니다.
- 왼쪽 자식 노드가 새로운 루트가 되고, 기존의 루트 노드는 왼쪽 자식 노드의 오른쪽 자식이 됩니다.
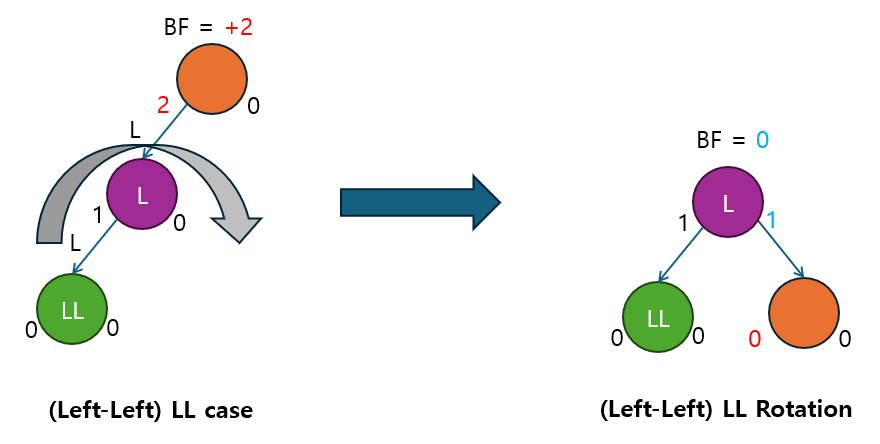
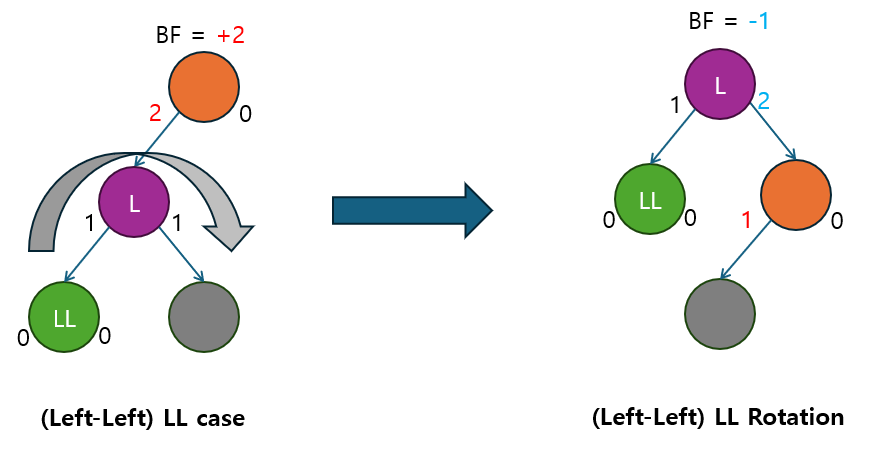
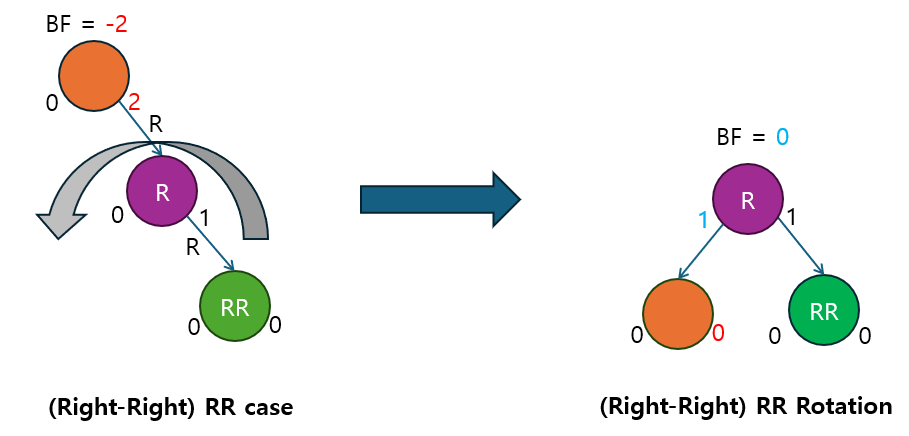
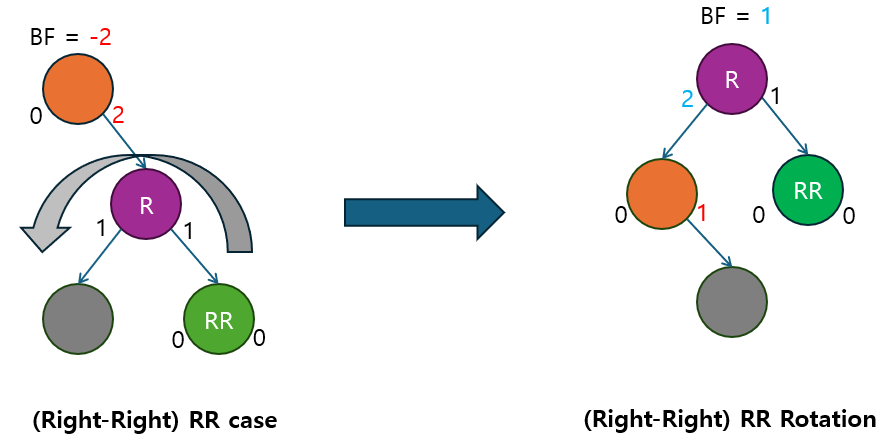
2.2.2 RR 회전 (Right-Right 회전)
- 오른쪽 자식이 오른쪽 서브트리를 가지는 RR 케이스 (Right-Right)에서 불균형을 해결하는 회전입니다.
- 오른쪽 자식 노드가 새로운 루트가 되고, 기존의 루트 노드는 오른쪽 자식 노드의 왼쪽 자식이 됩니다.
2.3 회전 연산 (Rotation) - 이중 회전 (Double Rotation)
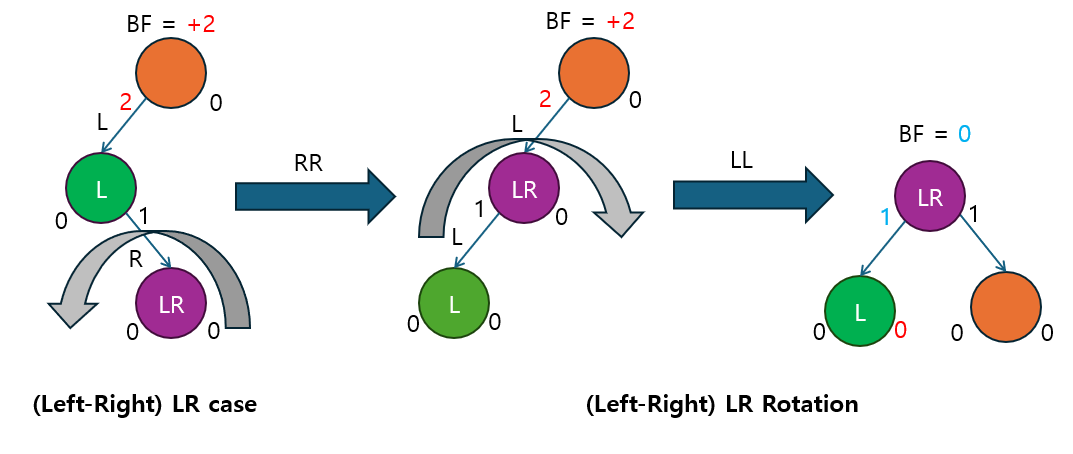
LR 회전 (Left-Right 회전)
- 왼쪽 자식이 오른쪽 서브트리를 가지는 LR 케이스 (Left-Right)에서 불균형을 해결하는 이중 회전입니다.
- 먼저 왼쪽 자식의 오른쪽 서브트리에 대해 RR 회전을 수행한 후, LL 회전을 적용합니다.
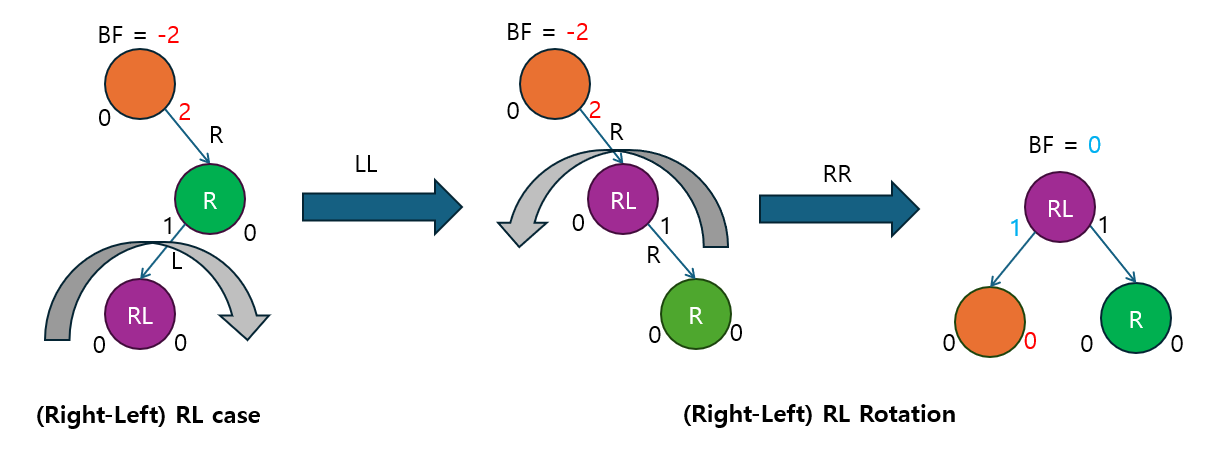
RL 회전 (Right-Left 회전)
- 오른쪽 자식이 왼쪽 서브트리를 가지는 RL 케이스 (Right-Left)에서 불균형을 해결하는 이중 회전입니다.
- 먼저 오른쪽 자식의 왼쪽 서브트리에 대해 LL 회전을 수행한 후, RR 회전을 적용합니다.
2.4 AVL 트리의 삽입 시 회전 동작
노드를 삽입할 때, AVL 트리는 삽입 후 트리의 균형이 깨질 수 있기 때문에 균형 인수(Balance Factor, BF)를 확인하면서 회전 연산이 필요할 수 있습니다.
- 트리의 균형 인수가
+2또는-2로 변화하면, 불균형 상태가 발생한 것입니다. - 이때 적절한 회전 연산을 수행하여 트리의 균형을 되찾습니다.
| 회전 종류 | 조건 (루트 노드의 BF) | 자식 노드의 BF 조건 | 설명 |
|---|---|---|---|
| LL 회전 | BF ≥ +2 | 왼쪽 자식의 BF ≥ 0 | 왼쪽 자식이 다시 왼쪽으로 치우친 경우. 단순 LL 회전으로 해결. |
| RR 회전 | BF ≤ -2 | 오른쪽 자식의 BF ≤ 0 | 오른쪽 자식이 다시 오른쪽으로 치우친 경우. 단순 RR 회전으로 해결. |
| LR 회전 | BF ≥ +2 | 왼쪽 자식의 BF < 0 | 왼쪽 자식이 오른쪽으로 치우친 경우. 먼저 RR 회전 후, LL 회전. |
| RL 회전 | BF ≤ -2 | 오른쪽 자식의 BF > 0 | 오른쪽 자식이 왼쪽으로 치우친 경우. 먼저 LL 회전 후, RR 회전. |
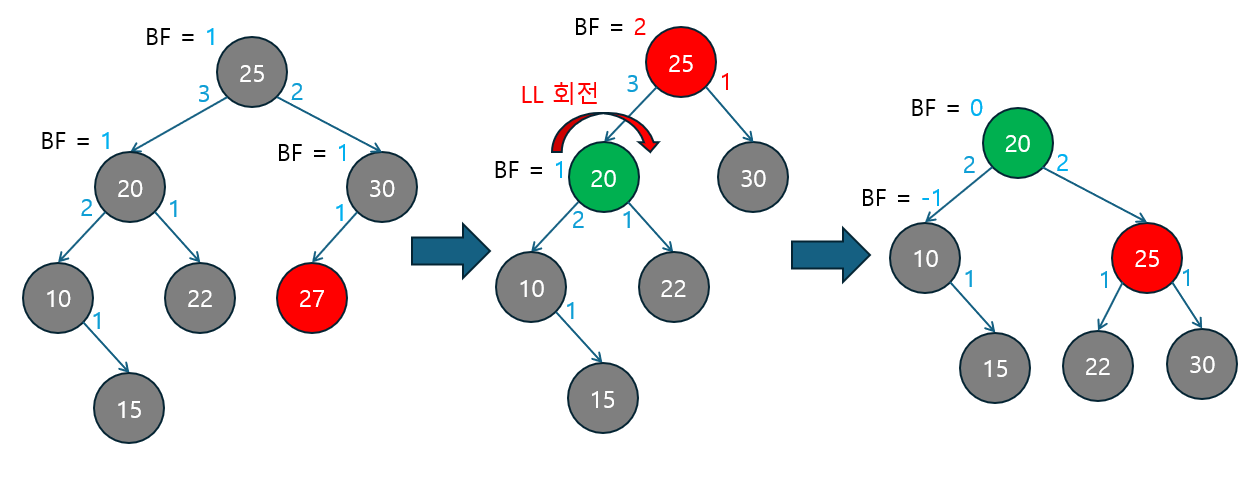
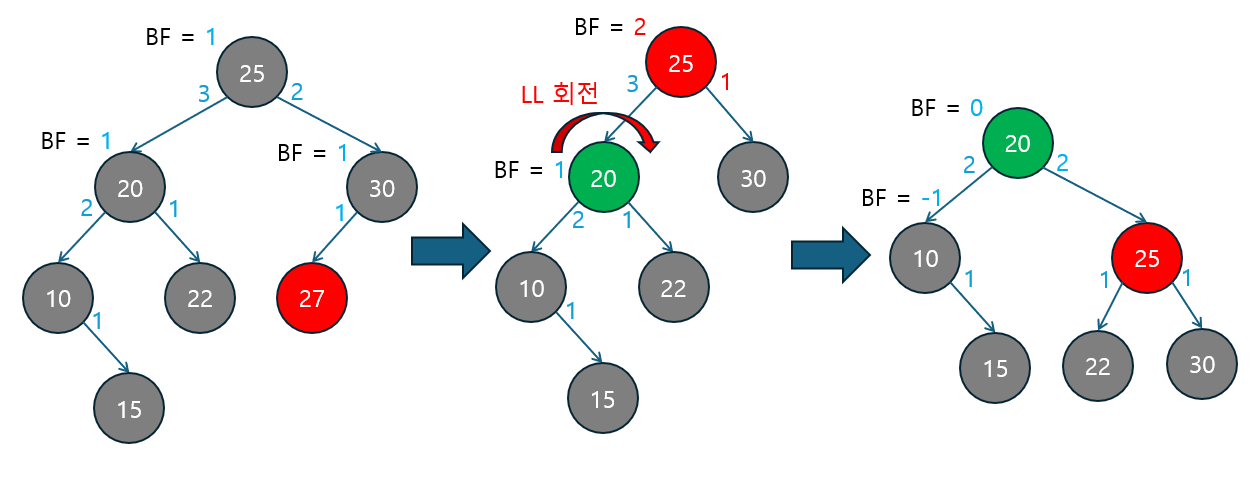
아래는 노드 삽입 후 발생하는 RR 케이스의 예시입니다.
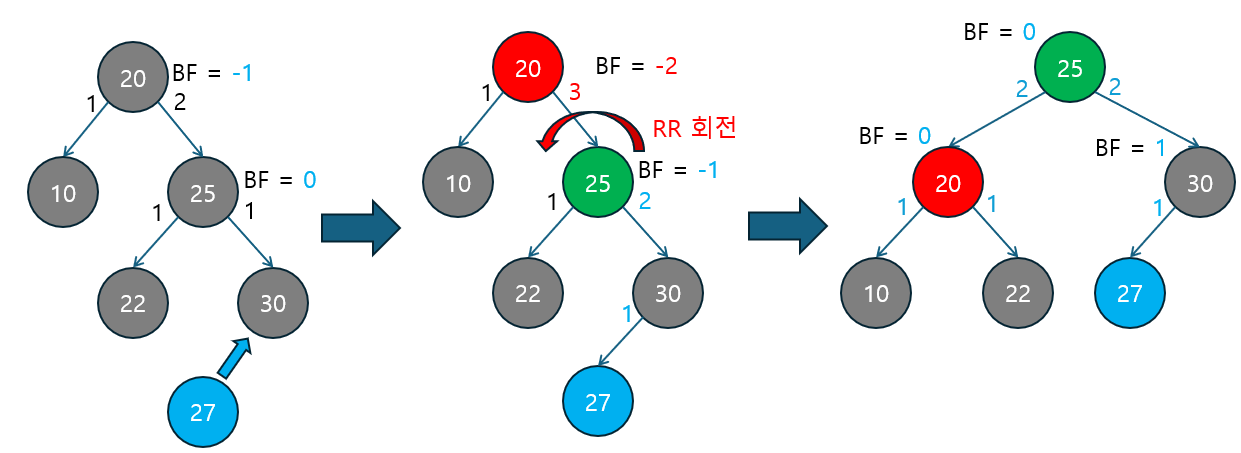
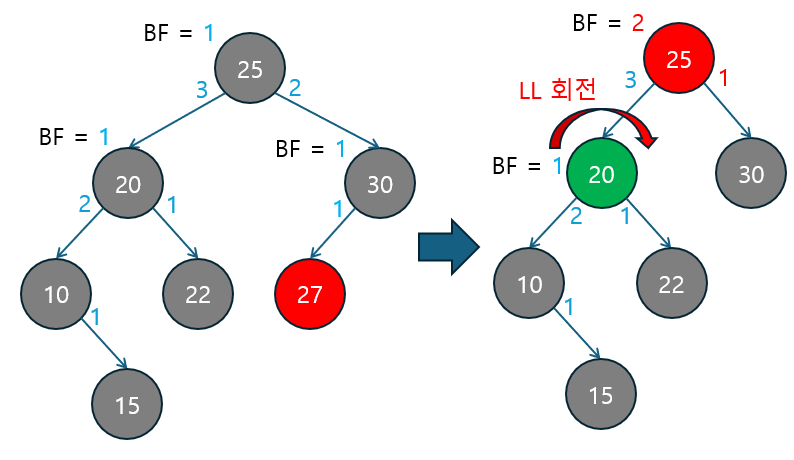
삽입 후 트리의 균형 상태 확인
- 초기 상태: 삽입 전에 각 노드의 균형 인수가 적절하게 유지되고 있습니다.
- 루트 노드
20의 BF는-1입니다. - 자식 노드
25의 BF는0으로 균형 상태에 있습니다.
- 루트 노드
삽입될 노드는 27이며, 이 삽입으로 인해 트리의 균형이 깨지게 됩니다.
- 노드 삽입: 노드
27을 노드30의 왼쪽 자식으로 삽입합니다.- 삽입 후, 삽입된 노드로부터 부모 노드와 조상 노드들의
균형 인수를 다시 계산합니다. - 노드
25는 왼쪽 서브트리의 높이보다 오른쪽 서브트리의 높이가 커져 균형 인수가-1로 변합니다. - 루트 노드
20은 오른쪽 서브트리의 높이가 왼쪽보다 3으로 커져서 균형 인수가-2가 됩니다. 이로 인해 불균형 상태가 발생합니다.
- 삽입 후, 삽입된 노드로부터 부모 노드와 조상 노드들의
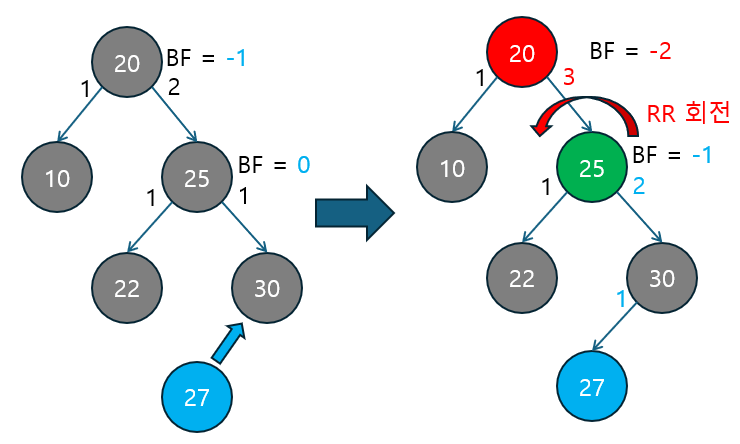
- RR 회전 (Right-Right 회전) 적용
- 불균형이 발생한 루트 노드
20의 균형 인수가-2이고 오른쪽 자식 노드의 균형 인수가-1로0보다 작거나 같기 때문에오른쪽 서브트리가 더 깊은 RR 케이스입니다. - RR 회전을 적용하여 트리의 균형을 맞춥니다:
- 노드
25가 새로운 루트가 되고, 노드20은 노드25의 왼쪽 자식으로 내려오면서 노드22는 노드20의 오른쪽 자식이 됩니다. - 노드
30과27은 회전 이후에도 같은 위치에 남아있습니다.
- 노드
- 불균형이 발생한 루트 노드
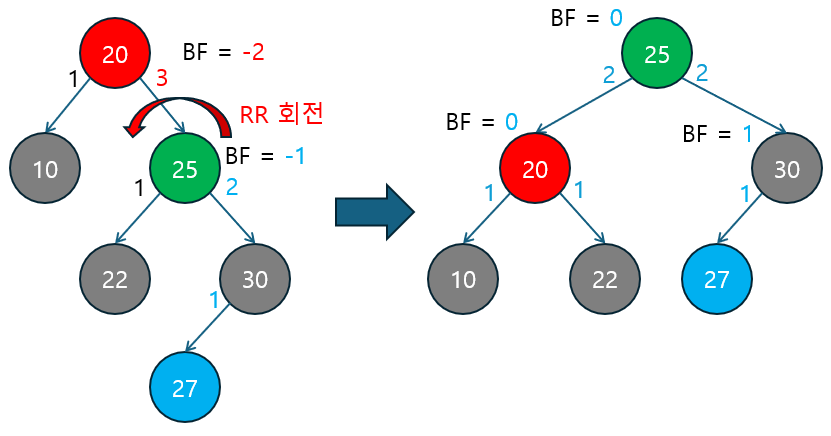
- 회전 후 결과
- 회전 후, 트리의 균형 인수는 모두
0또는1로 유지되어 균형 상태를 되찾았습니다.- 새로운 루트
25의 균형 인수는0이 됐습니다. - 왼쪽 자식 노드
20과 오른쪽 자식 노드30도 각각 균형 인수가0또는1로 맞춰졌습니다.
- 새로운 루트
- 회전 후, 트리의 균형 인수는 모두
이 예시에서는 노드 삽입 후 트리의 균형이 깨졌을 때, RR 회전을 통해 트리가 다시 균형을 되찾는 과정을 볼 수 있었습니다.
- 이처럼 AVL 트리에서는 삽입 후 균형이 깨지면 적절한 회전을 통해 트리의 높이를 균형 있게 유지할 수 있습니다.
2.5 AVL 트리의 삭제 시 회전 동작
AVL 트리에서 노드를 삭제할 때도 삽입과 마찬가지로 트리의 균형이 깨질 수 있습니다.
- 삭제 후에는 균형 인수(Balance Factor, BF)를 다시 확인하면서, 불균형이 발생하면 적절한 회전 연산을 통해 트리의 균형을 맞춰야 합니다.
| 회전 종류 | 조건 (루트 노드의 BF) | 자식 노드의 BF 조건 | 설명 |
|---|---|---|---|
| LL 회전 | BF ≥ +2 | 왼쪽 자식의 BF ≥ 0 | 왼쪽 자식이 다시 왼쪽으로 치우친 경우. 단순 LL 회전으로 해결. |
| RR 회전 | BF ≤ -2 | 오른쪽 자식의 BF ≤ 0 | 오른쪽 자식이 다시 오른쪽으로 치우친 경우. 단순 RR 회전으로 해결. |
| LR 회전 | BF ≥ +2 | 왼쪽 자식의 BF < 0 | 왼쪽 자식이 오른쪽으로 치우친 경우. 먼저 RR 회전 후, LL 회전. |
| RL 회전 | BF ≤ -2 | 오른쪽 자식의 BF > 0 | 오른쪽 자식이 왼쪽으로 치우친 경우. 먼저 LL 회전 후, RR 회전. |
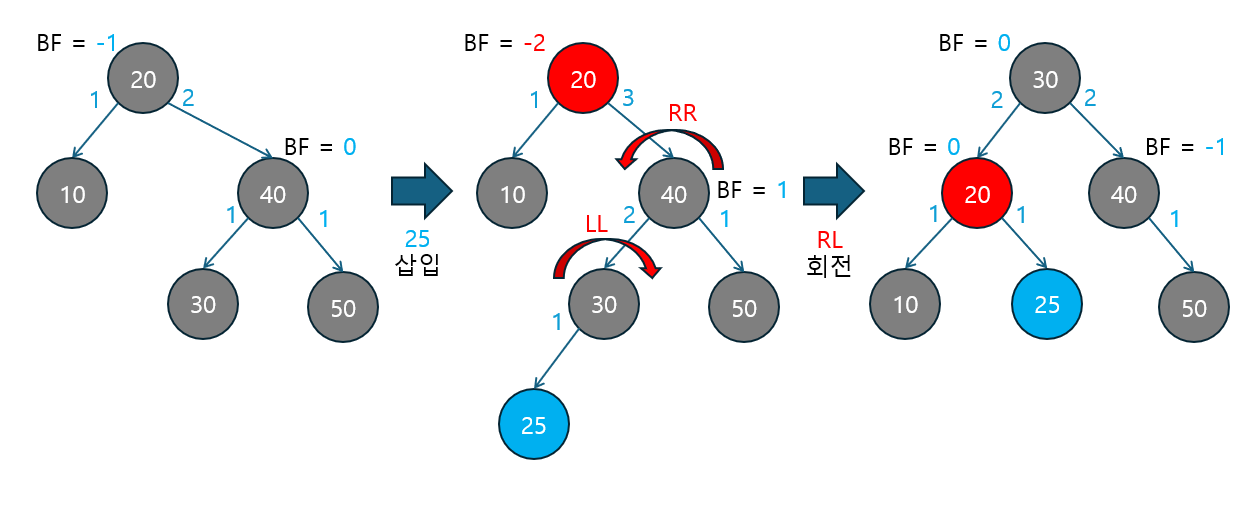
아래 예시는 노드 삭제 후 LL 회전을 통해 트리의 균형을 맞추는 과정을 보여줍니다.
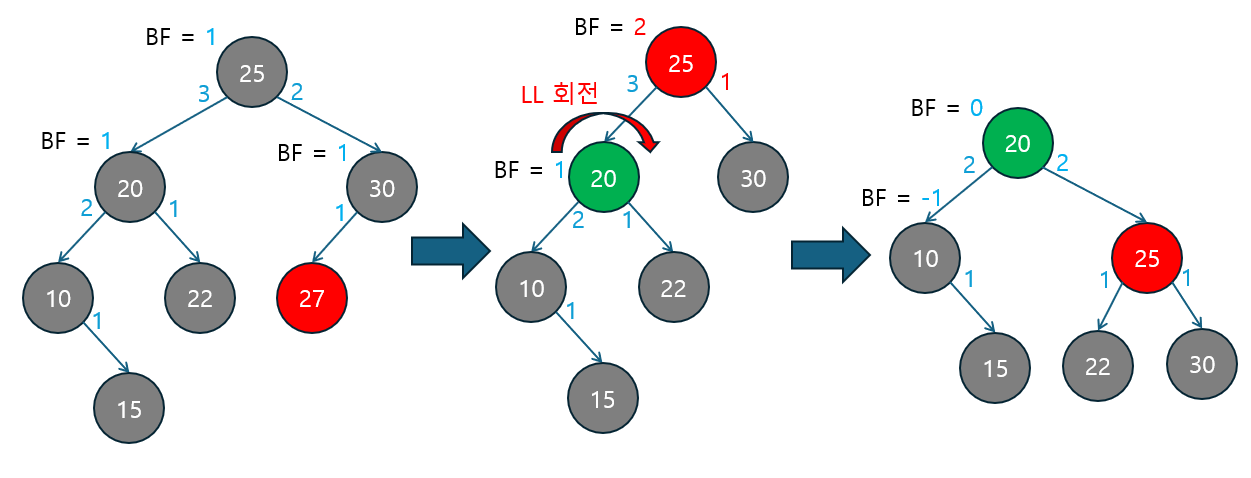
삭제 후 트리의 균형 상태 확인
-
초기 상태: 삭제 전에 트리의 각 노드의 균형 인수는 적절히 유지되고 있습니다.
- 루트 노드
25의 BF는1입니다. - 왼쪽 자식 노드
20의 BF는1입니다. - 오른쪽 자식 노드
30의 BF는1입니다. - 삭제 대상은 노드
27입니다.
- 루트 노드
-
노드 삭제: 노드
27을 삭제합니다.- 삭제 후, 부모 노드
30의 오른쪽 자식이 없어져 서브트리의 높이가 감소하고, 그로 인해 부모 노드들의 균형 인수가 변하게 됩니다. - 노드
30의 균형 인수는0으로 감소했고, 부모 노드25의 균형 인수가+2로 변하여 불균형 상태가 됩니다.
- 삭제 후, 부모 노드
LL 회전 (Left-Left 회전) 적용
- 불균형이 발생한 노드
25는 왼쪽 서브트리가 오른쪽 서브트리보다2만큼 크고, 그 왼쪽 자식 노드의 균형 인수가1로0보다 크거나 같아서왼쪽 서브트리가 더 깊은 LL 케이스에 해당합니다. - 따라서 LL 회전을 통해 트리의 균형을 맞춥니다:
- 노드
20이 새로운 루트가 되고, 노드25는 오른쪽 자식으로 내려가고, 노드22는 노드25의 왼쪽 자식이 됩니다. - 회전 후에도
30,10,15노드의 위치는 변하지 않습니다.
- 노드
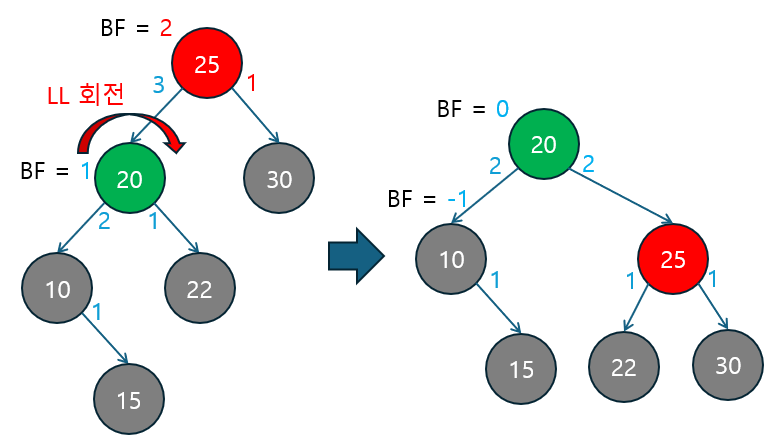
회전 후 결과
- 회전 후, 트리의 균형 인수는 모두 적절히 조정되어 균형을 되찾습니다.
- 새로운 루트 노드
20의 균형 인수는0이 됐습니다. - 왼쪽 자식
10의 BF는-1, 오른쪽 자식25의 BF는0입니다.
- 새로운 루트 노드
- 결론적으로 전체 트리가 균형을 유지합니다.
위 예시는 노드 삭제 후 트리의 균형이 깨질 때, LL 회전을 통해 트리가 다시 균형을 유지하는 과정을 시각적으로 볼 수 있었습니다.
- 이처럼 노드 삭제 후 불균형이 감지되면, 삽입 때와 마찬가지로 해당 회전 연산(LL, RR, LR, RL)을 적용하여 트리의 균형을 맞출 수 있습니다.
3. AVL Tree 구현 (Java, Python)
3.1 Java로 AVL Tree 구현
먼저, Java로 AVL 트리를 구현하는 방법을 살펴보겠습니다. AVL 트리의 핵심 기능인 삽입, 삭제, 균형 유지(회전 연산)을 구현할 것입니다.
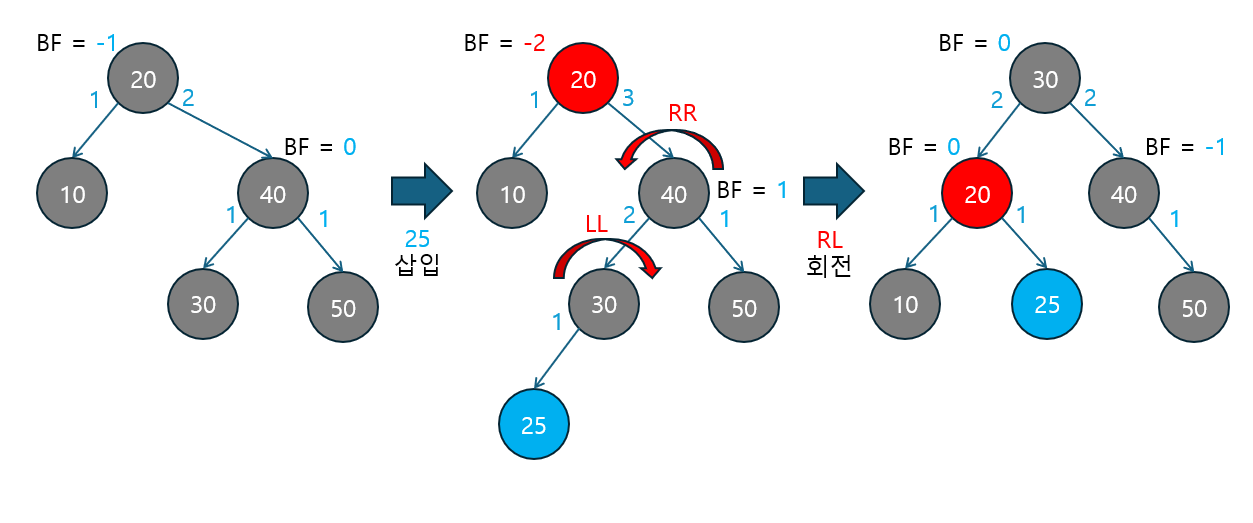
3.1.1 노드 클래스 정의
먼저 각 노드를 정의하는 클래스를 작성합니다.
- 노드는 왼쪽 자식, 오른쪽 자식, 그리고 트리의 균형을 위해 높이 정보를 저장합니다.
class Node {
int key, height;
Node left, right;
Node(int d) {
key = d;
height = 1;
}
}3.1.2 AVL Tree 클래스 정의 & 삽입 연산 코드 작성
이제 AVL 트리 클래스에서 주요 연산들을 구현합니다.
- height: 노드의 높이를 반환합니다.
- getBalance: 노드의 균형 인수(BF)를 계산합니다.
- rightRotate: 오른쪽으로 회전하는 연산입니다.
- leftRotate: 왼쪽으로 회전하는 연산입니다.
- insert: 새로운 노드를 트리에 삽입합니다.
class AVLTree {
Node root;
// 높이 반환
int height(Node N) {
if (N == null)
return 0;
return N.height;
}
// 균형 인수 계산
int getBalance(Node N) {
if (N == null)
return 0;
return height(N.left) - height(N.right);
}
// 오른쪽 회전
Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
// 회전 수행
x.right = y;
y.left = T2;
// 높이 업데이트
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
// 왼쪽 회전
Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
// 회전 수행
y.left = x;
x.right = T2;
// 높이 업데이트
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y;
}
// 노드 삽입
Node insert(Node node, int key) {
if (node == null)
return (new Node(key));
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
else
return node;
// 높이 업데이트
node.height = 1 + Math.max(height(node.left), height(node.right));
// 균형 확인
int balance = getBalance(node);
// LL 케이스
if (balance > 1 && key < node.left.key)
return rightRotate(node);
// RR 케이스
if (balance < -1 && key > node.right.key)
return leftRotate(node);
// LR 케이스
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL 케이스
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 노드를 전위 순회하며 출력 (테스트 용도)
void preOrder(Node node) {
if (node != null) {
System.out.print(node.key + " ");
preOrder(node.left);
preOrder(node.right);
}
}
public static void main(String[] args) {
AVLTree tree = new AVLTree();
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 30);
tree.root = tree.insert(tree.root, 40);
tree.root = tree.insert(tree.root, 50);
tree.root = tree.insert(tree.root, 25);
System.out.println("Preorder traversal of constructed AVL tree is:");
tree.preOrder(tree.root); // 30 20 10 25 40 50
}
}- 이 Java 코드는 AVL 트리의 삽입과 회전 연산을 처리한 뒤, 전위 순회로 트리의 결과를 출력합니다. 위 예제에서는
6개의 노드가 삽입되며, 불균형이 발생할 때마다 적절한 회전 연산이 수행됩니다.
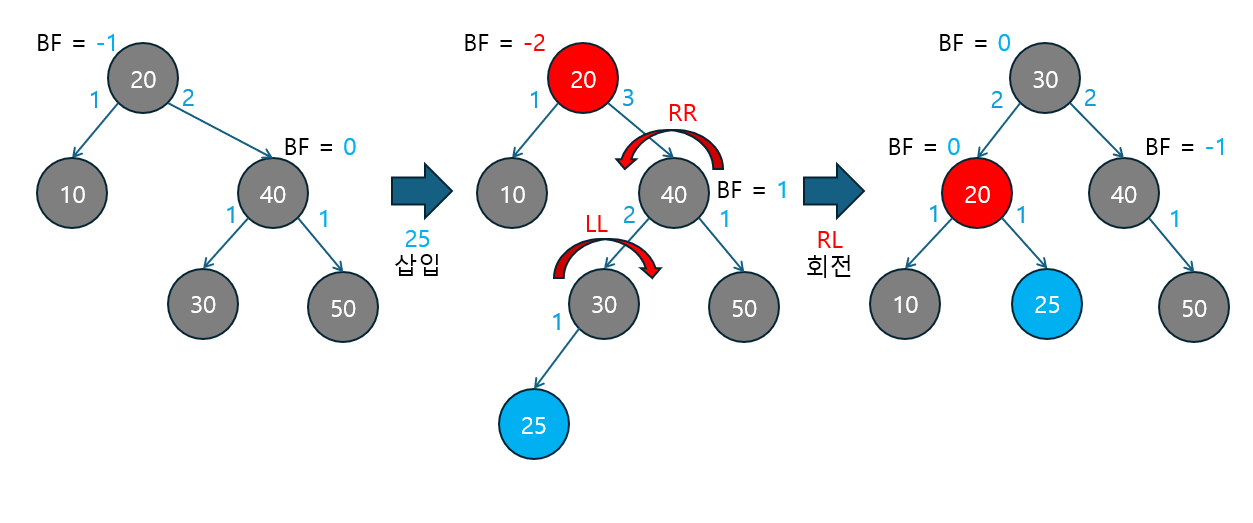
3.1.3 AVL Tree 노드 삭제 연산 추가
이번에는 AVL 트리에서 노드를 삭제하는 방법을 살펴보겠습니다.
- 노드 삭제는 삽입과 유사하지만, 삭제 후 트리의 균형을 유지하기 위해 추가적인 회전 연산이 필요합니다.
class AVLTree {
// ... 이전 코드 생략 ...
// 삭제 연산
Node deleteNode(Node root, int key) {
// 기본적인 이진 검색 트리 삭제 연산
if (root == null)
return root;
if (key < root.key)
root.left = deleteNode(root.left, key);
else if (key > root.key)
root.right = deleteNode(root.right, key);
else {
// 삭제할 노드 찾음
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
if (temp == null) {
temp = root;
root = null;
} else
root = temp;
} else {
Node temp = minValueNode(root.right);
root.key = temp.key;
root.right = deleteNode(root.right, temp.key);
}
}
// 트리가 한 노드도 없는 경우
if (root == null)
return root;
// 높이 갱신
root.height = Math.max(height(root.left), height(root.right)) + 1;
// 균형 확인
int balance = getBalance(root);
// LL 케이스
if (balance > 1 && getBalance(root.left) >= 0)
return rightRotate(root);
// LR 케이스
if (balance > 1 && getBalance(root.left) < 0) {
root.left = leftRotate(root.left);
return rightRotate(root);
}
// RR 케이스
if (balance < -1 && getBalance(root.right) <= 0)
return leftRotate(root);
// RL 케이스
if (balance < -1 && getBalance(root.right) > 0) {
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
// 최소값을 찾는 함수 (오른쪽 서브트리에서 가장 작은 값)
Node minValueNode(Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
}
이 코드는 노드 삭제 후 AVL 트리의 균형을 맞추기 위해 회전 연산을 수행합니다.
- 기본적인 이진 검색 트리 방식으로 노드를 삭제한 후, 트리의 균형 인수를 확인하여 불균형이 발생한 경우 회전 연산을 적용합니다.
3.2 Python으로 AVL Tree 구현
이번에는 Python을 사용하여 동일한 AVL 트리 구현을 해보겠습니다. 기본적인 구조와 논리는 Java와 동일하지만 Python 문법에 맞춰 구현합니다.
3.2.1 노드 클래스 정의
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 13.2.2 AVL Tree 클래스 정의
AVL 트리 클래스는 삽입과 회전, 그리고 균형 인수를 계산하는 메서드로 구성됩니다.
class AVLTree:
# 노드 높이 반환
def height(self, root):
if not root:
return 0
return root.height
# 균형 인수 반환
def get_balance(self, root):
if not root:
return 0
return self.height(root.left) - self.height(root.right)
# 오른쪽 회전
def right_rotate(self, y):
x = y.left
T2 = x.right
x.right = y
y.left = T2
y.height = 1 + max(self.height(y.left), self.height(y.right))
x.height = 1 + max(self.height(x.left), self.height(x.right))
return x
# 왼쪽 회전
def left_rotate(self, x):
y = x.right
T2 = y.left
y.left = x
x.right = T2
x.height = 1 + max(self.height(x.left), self.height(x.right))
y.height = 1 + max(self.height(y.left), self.height(y.right))
return y
# 삽입 연산
def insert(self, root, key):
if not root:
return Node(key)
if key < root.key:
root.left = self.insert(root.left, key)
elif key > root.key:
root.right = self.insert(root.right, key)
else:
return root
root.height = 1 + max(self.height(root.left), self.height(root.right))
balance = self.get_balance(root)
# LL 케이스
if balance > 1 and key < root.left.key:
return self.right_rotate(root)
# RR 케이스
if balance < -1 and key > root.right.key:
return self.left_rotate(root)
# LR 케이스
if balance > 1 and key > root.left.key:
root.left = self.left_rotate(root.left)
return self.right_rotate(root)
# RL 케이스
if balance < -1 and key < root.right.key:
root.right = self.right_rotate(root.right)
return self.left_rotate(root)
return root
# 전위 순회 출력
def pre_order(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.pre_order(root.left)
self.pre_order(root.right)
# 실행 테스트
tree = AVLTree()
root = None
root = tree.insert(root, 10)
root = tree.insert(root, 20)
root = tree.insert(root, 30)
root = tree.insert(root, 40)
root = tree.insert(root, 50)
root = tree.insert(root, 25)
print("Preorder traversal of the constructed AVL tree is:")
tree.pre_order(root) # 30 20 10 25 40 50
Python 코드는 Java 코드와 마찬가지로 노드 삽입과 회전 연산을 처리하며, 전위 순회로 트리의 결과를 출력합니다. 삽입 과정에서 적절한 회전 연산이 수행되어 트리의 균형을 유지합니다.
3.2.3 AVL Tree 노드 삭제 (Python)
이번에는 Python으로 노드 삭제 연산을 구현해 보겠습니다.
class AVLTree:
# 이전 코드 생략
# 삭제 연산
def delete(self, root, key):
if not root:
return root
if key < root.key:
root.left = self.delete(root.left, key)
elif key > root.key:
root.right = self.delete(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.get_min_value_node(root.right)
root.key = temp.key
root.right = self.delete(root.right, temp.key)
if root is None:
return root
root.height = 1 + max(self.height(root.left), self.height(root.right))
balance = self.get_balance(root)
# LL 케이스
if balance > 1 and self.get_balance(root.left) >= 0:
return self.right_rotate(root)
# LR 케이스
if balance > 1 and self.get_balance(root.left) < 0:
root.left = self.left_rotate(root.left)
return self.right_rotate(root)
# RR 케이스
if balance < -1 and self.get_balance(root.right) <= 0:
return self.left_rotate(root)
# RL 케이스
if balance < -1 and self.get_balance(root.right) > 0:
root.right = self.right_rotate(root.right)
return self.left_rotate(root)
return root
# 최소값 찾기 (오른쪽 서브트리에서)
def get_min_value_node(self, root):
if root is None or root.left is None:
return root
return self.get_min_value_node(root.left)
Python 코드 역시 노드 삭제 후 트리의 균형을 맞추기 위해 회전 연산을 수행하며, 기본적인 삭제 연산 후 균형 인수를 확인해 불균형이 발생한 경우 적절한 회전 연산을 적용합니다.
마무리
이번 포스팅에서는 AVL 트리의 기본 개념부터 시작해, 삽입 및 삭제 시 발생하는 불균형을 회전 연산을 통해 해결하는 방식을 살펴보았습니다. 또한, Java와 Python을 통해 AVL 트리의 주요 연산을 구현하는 방법도 다루었습니다.
핵심 요약:
- AVL 트리는 균형 이진 탐색 트리로, 모든 노드에서 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 최대 1이 되도록 유지하는 구조입니다.
- 트리의 균형이 깨질 경우 4가지 회전 연산(LL, RR, LR, RL)을 사용해 트리의 높이를 조정합니다.
- 시간 복잡도는 삽입, 삭제, 탐색 모두에서 O(log n)을 보장하기 때문에, 특히 탐색 성능이 중요한 데이터 구조에 적합합니다.
AVL 트리의 장점:
- 탐색, 삽입, 삭제 연산 모두에서 O(log n)의 성능을 보장하므로, 균형이 유지된 상태에서 성능 저하 없이 연산을 수행할 수 있습니다.
- 트리의 균형을 유지하므로, 최악의 경우에도 탐색 시간이 빠릅니다.
AVL 트리의 단점:
- 삽입과 삭제 시 회전 연산이 추가되므로, 삽입/삭제가 매우 빈번한 경우엔 그 성능이 저하될 수 있습니다.
- 구현이 상대적으로 복잡하기 때문에, 트리 구조의 내부 동작을 잘 이해해야 합니다.
실제 활용:
- AVL 트리는 데이터 구조의 탐색 성능이 중요한 시스템에서 사용됩니다. 특히, 검색 엔진, 데이터베이스 시스템과 같은 동적 데이터가 많은 환경에서 성능을 유지하는 데 중요한 역할을 합니다.
- 하지만 실무에서는 레드-블랙 트리와 같은 더 효율적인 자료구조가 더 많이 사용되며, AVL 트리는 데이터의 정확한 균형 유지가 필요한 특정한 경우에 주로 사용됩니다.
다음 포스팅에서는 또 다른 대표적인 균형 이진 탐색 트리인 레드-블랙 트리(Red-Black Tree)에 대해 다룰 예정입니다.
