[자료구조] Tree - Heap 자료구조와 PriorityQueue

Kyung Jae, Cheong·2024년 10월 16일

Java python 자료구조

자료구조-DataStructure

목록 보기

14/19

본 시리즈는 프로그래밍 자료구조의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
- IDE : IntelliJ IDEA (Ultimate Edition)
- Java : JDK 21 (corretto-21)
- Python : 3.9 (conda env)

트리(Tree) - Heap & PriorityQueue

일반적인 Tree에 대한 전반적인 내용들은 다음 포스팅에서 확인하실 수 있습니다.
- [자료구조] Tree - 개요 (기본 개념과 구현)
이진트리에 대한 기본적인 내용들은 다음 포스팅에서 확인하실 수 있습니다.
- [자료구조] Tree - Binary Tree (이진 트리) - 개념과 구현

1. Heap 자료구조란?

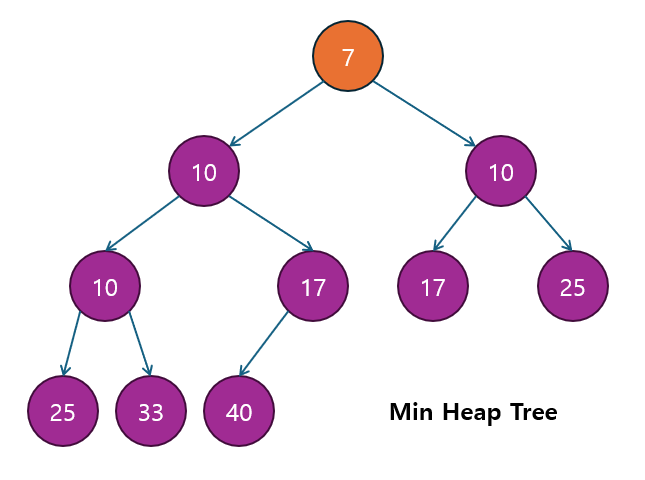
Heap은 완전 이진 트리(Complete Binary Tree)의 일종으로, 우선순위 큐(Priority Queue)와 같은 최대값 또는 최소값을 빠르게 찾기 위한 자료구조입니다.

Heap의 핵심 개념은 각 노드가 부모-자식 간의 우선순위 규칙을 만족한다는 것입니다.
주로 최소 힙(Min Heap)과 최대 힙(Max Heap)으로 나뉘어 사용됩니다.

1.1 Heap의 특징

완전 이진 트리(Complete Binary Tree): 힙은 완전 이진 트리의 구조를 가지며, 마지막 레벨을 제외한 모든 레벨이 꽉 차 있고, 마지막 레벨은 왼쪽에서부터 차례대로 채워집니다.
우선순위 규칙: 힙에서는 부모 노드가 자식 노드보다 우선순위가 높습니다. 여기서 우선순위는 대표적으로 두 가지 규칙으로 나뉩니다.
- 최소 힙(Min Heap): 부모 노드의 값이 자식 노드보다 작거나 같습니다. 따라서 루트 노드는 항상 최소값을 가집니다. (PriorityQueue가 기본적으로 최소힙으로 동작합니다)
- 최대 힙(Max Heap): 부모 노드의 값이 자식 노드보다 크거나 같습니다. 따라서 루트 노드는 항상 최대값을 가집니다.
배열로 구현 가능: 힙은 완전 이진 트리(Complete Binary Tree)이기 때문에 배열을 이용하여 쉽게 구현할 수 있습니다. 부모와 자식 노드 간의 관계는 배열의 인덱스를 통해 계산됩니다.
- 부모 인덱스 : i
- 왼쪽 자식: 2 * i + 1
- 오른쪽 자식: 2 * i + 2

(참고) Java에서의 Heap과 메모리 영역

특히 Java에서는 Heap 자료구조와 Heap 메모리 영역이 완전히 다른 개념입니다.

Heap 메모리는 프로그램 실행 중 동적으로 할당되는 메모리 영역을 의미하고, Heap 자료구조는 우선순위 규칙을 만족하는 완전 이진 트리를 의미하므로 혼동하지 않도록 주의해야 합니다.

왜 두 개념이 함께 쓰이는지는 Heap이라는 용어 자체의 뜻을 알아봐야합니다.

Heap은 무언가를 쌓다, 무더기, 더미라는 뜻을 가지는 영어 단어입니다.

Heap 자료구조와 Heap 메모리 영역 모두 어떤 의미에선 위 영어 단어의 뜻을 반영하는 개념이기 때문에 같은 이름이 지어진 것으로 여겨집니다.

결론적으로, 두 개념은 완전히 다른 것이라는 점을 기억하시면 됩니다.

1.2 Heap의 용도

Heap 자료구조는 다양한 알고리즘과 응용 분야에서 매우 중요한 역할을 합니다. 그 대표적인 용도들을 살펴보면 다음과 같습니다:

우선순위 큐(Priority Queue)

힙은 우선순위 큐의 가장 기본적인 자료구조로 사용됩니다.
우선순위 큐는 데이터들에 우선순위를 부여하고, 우선순위가 높은 데이터를 먼저 처리하는 큐(Queue)입니다.
최소 힙을 사용하면 우선순위가 가장 낮은 값을 먼저 처리하고, 최대 힙을 사용하면 우선순위가 가장 높은 값을 먼저 처리합니다.
Java와 Python의 PriorityQueue는 기본적으로 최소 힙을 기반으로 구현되어 있으며, Java에선 필요에 따라 Comparator 등을 사용해 최대 힙처럼 동작하게 할 수 있습니다. (다만, Python은 음수로 변환하는 별도의 과정이 필요합니다.)

힙 정렬(Heap Sort)

힙을 이용하여 정렬 알고리즘을 구현할 수도 있습니다.
힙 정렬은 최대 힙을 사용하여 배열을 내림차순으로, 최소 힙을 사용하여 배열을 오름차순으로 정렬할 수 있습니다.
힙 정렬은 최악의 경우에도 O(n log n)의 시간 복잡도를 보장하며, 안정적인 정렬 알고리즘으로 알려져 있습니다.

최소 신장 트리(Minimum Spanning Tree)

Prim's Algorithm과 같은 최소 신장 트리 알고리즘에서는 우선순위 큐로 힙을 사용하여 가장 적은 비용으로 그래프의 모든 노드를 연결할 수 있습니다.

최단 경로 알고리즘(Shortest Path Algorithm)

다익스트라(Dijkstra) 알고리즘은 힙을 사용하여 최소 비용 경로를 빠르게 계산합니다.
- 우선순위 큐를 이용해 현재까지 계산된 최단 경로에서 가장 짧은 경로를 선택하고, 다른 노드들과의 경로를 갱신해 나가는 방식입니다.

실시간 작업 스케줄링

운영체제(OS)에서는 힙을 사용하여 작업 스케줄링을 관리합니다.
- 각 작업의 우선순위에 따라 작업을 처리해야 할 때 우선순위 큐로 구현된 힙이 효율적으로 스케줄링을 할 수 있습니다.

이벤트 시뮬레이션

이벤트가 발생하는 순서대로 처리해야 하는 시뮬레이션 프로그램에서, 힙을 사용해 시간 우선순위에 따른 이벤트 처리를 할 수 있습니다.

이처럼 힙 자료구조는 **우선순위 처리, 정렬, 그래프 탐색, 스케줄링** 등 다양한 분야에서 필수적인 자료구조로 활용됩니다.

2. Priority Queue의 개념

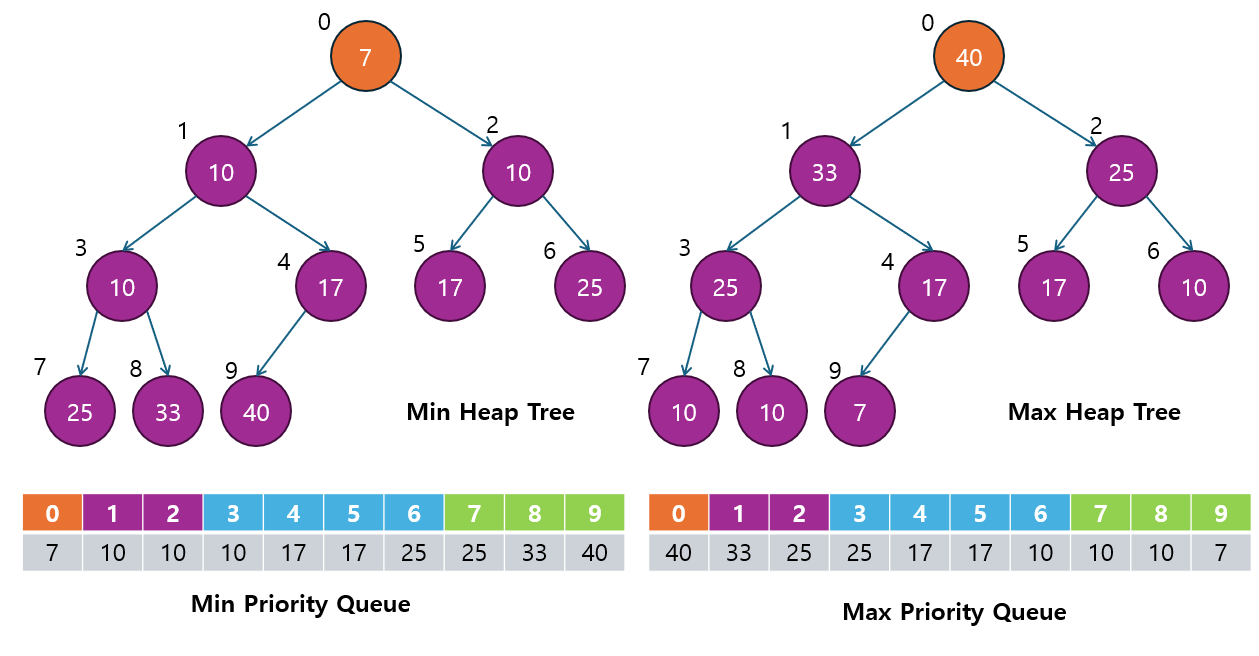
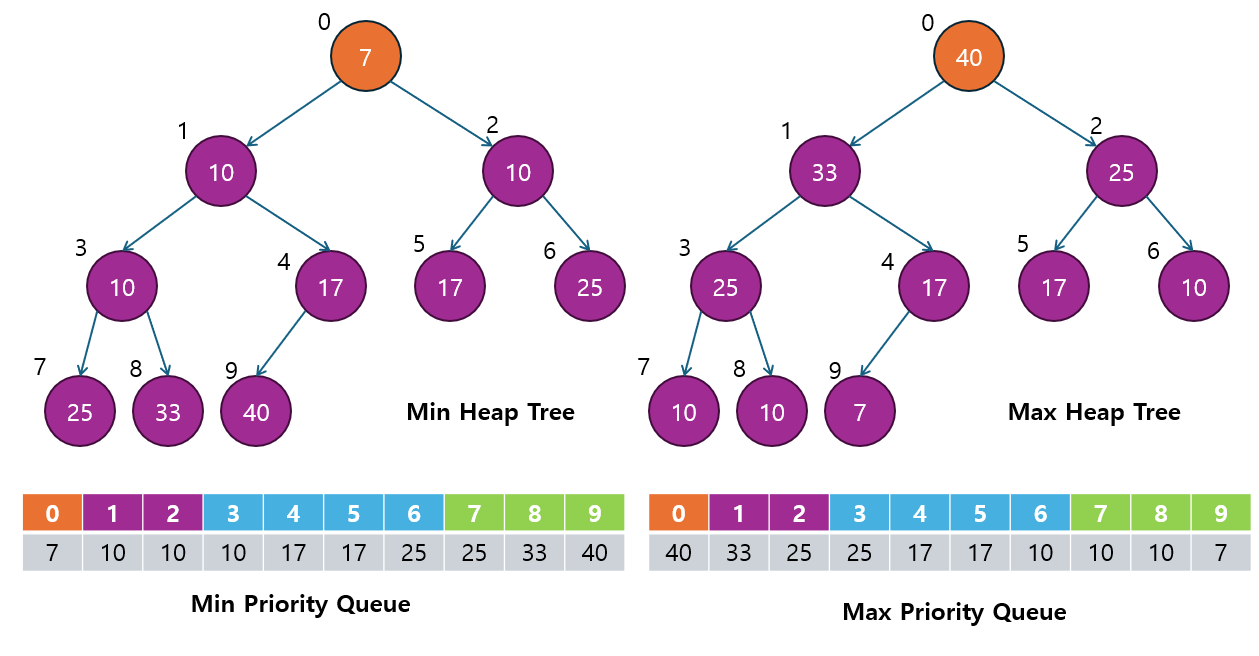
Priority Queue(우선순위 큐)는 큐(Queue)의 일종이지만, 일반적인 큐와는 다르게 우선순위에 따라 요소가 처리되는 자료구조입니다.

일반적인 큐는 FIFO(First In, First Out) 구조로, 먼저 들어온 데이터가 먼저 처리됩니다.
반면, 우선순위 큐는 우선순위가 높은 데이터가 먼저 처리됩니다.
- 즉, 먼저 들어온 데이터가 아니라, 가장 중요한 데이터가 먼저 처리되는 구조입니다.

2.1 Priority Queue의 주요 특징

우선순위 기준: 각 요소가 우선순위(priority)를 가지고 있으며, 큐는 이를 기준으로 요소를 정렬합니다.
- 최소 우선순위 큐(Min Priority Queue): 우선순위가 가장 낮은 요소가 먼저 처리됩니다. (기본적으로 Min Heap 기반)
- 최대 우선순위 큐(Max Priority Queue): 우선순위가 가장 높은 요소가 먼저 처리됩니다. (기본적으로 Max Heap 기반)
힙 기반 구현: Priority Queue는 일반적으로 힙(Heap)을 기반으로 구현됩니다.
- Min Heap 또는 Max Heap 구조를 사용하여 삽입과 삭제 연산을 O(log n)의 시간 복잡도로 처리할 수 있습니다.

2.2 Priority Queue의 동작 방식

1. 삽입(Insertion): 새로운 요소는 우선순위에 따라 힙의 규칙을 유지하면서 삽입됩니다.

예를 들어, Min Heap 기반 우선순위 큐라면, 새로운 요소는 부모보다 작으면 부모와 자리를 바꾸는 방식으로 적절한 위치에 삽입됩니다.

2. 삭제(Deletion): 가장 우선순위가 높은 (또는 낮은) 요소가 제거됩니다.

이는 힙의 루트에 해당하는 요소가 제거되고, 마지막 요소가 루트로 올라가면서 힙 규칙에 따라 다시 정렬됩니다.

3. 최댓값/최솟값 반환: Priority Queue는 언제나 우선순위가 가장 높은 (혹은 낮은) 요소를 빠르게 찾을 수 있습니다.

루트 노드가 항상 우선순위가 가장 높은 요소를 가지기 때문에, 바로 O(1) 시간에 최댓값 또는 최솟값을 반환할 수 있습니다.

2.3 우선순위 큐의 구현 방식

우선순위 큐는 여러 가지 방식으로 구현할 수 있으며, 각 방식은 삽입과 삭제의 효율성에 차이가 있습니다.

배열을 이용한 구현: 배열을 정렬된 상태로 유지하며, 우선순위에 따라 삽입 및 삭제를 진행합니다.
- 단점: 삽입 시 배열을 재정렬해야 하므로 O(n)의 시간 복잡도가 발생할 수 있습니다.
연결 리스트를 이용한 구현: 우선순위 순서대로 정렬된 연결 리스트를 유지합니다.
- 단점: 삽입이나 삭제 시 정렬된 리스트를 유지하기 위해 O(n)의 시간이 필요할 수 있습니다.
Heap(힙)을 이용한 구현: 가장 일반적인 방식으로, Min Heap 또는 Max Heap을 사용하여 삽입과 삭제를 O(log n) 시간에 처리합니다.
- 장점: 삽입, 삭제, 탐색이 모두 효율적으로 수행됩니다.

다음 파트에서는 Java와 Python에서 Priority Queue를 어떻게 구현하는지 알아볼 것입니다.

3. Java와 Python에서의 Priority Queue 구현

3.1 Java에서 PriorityQueue 구현

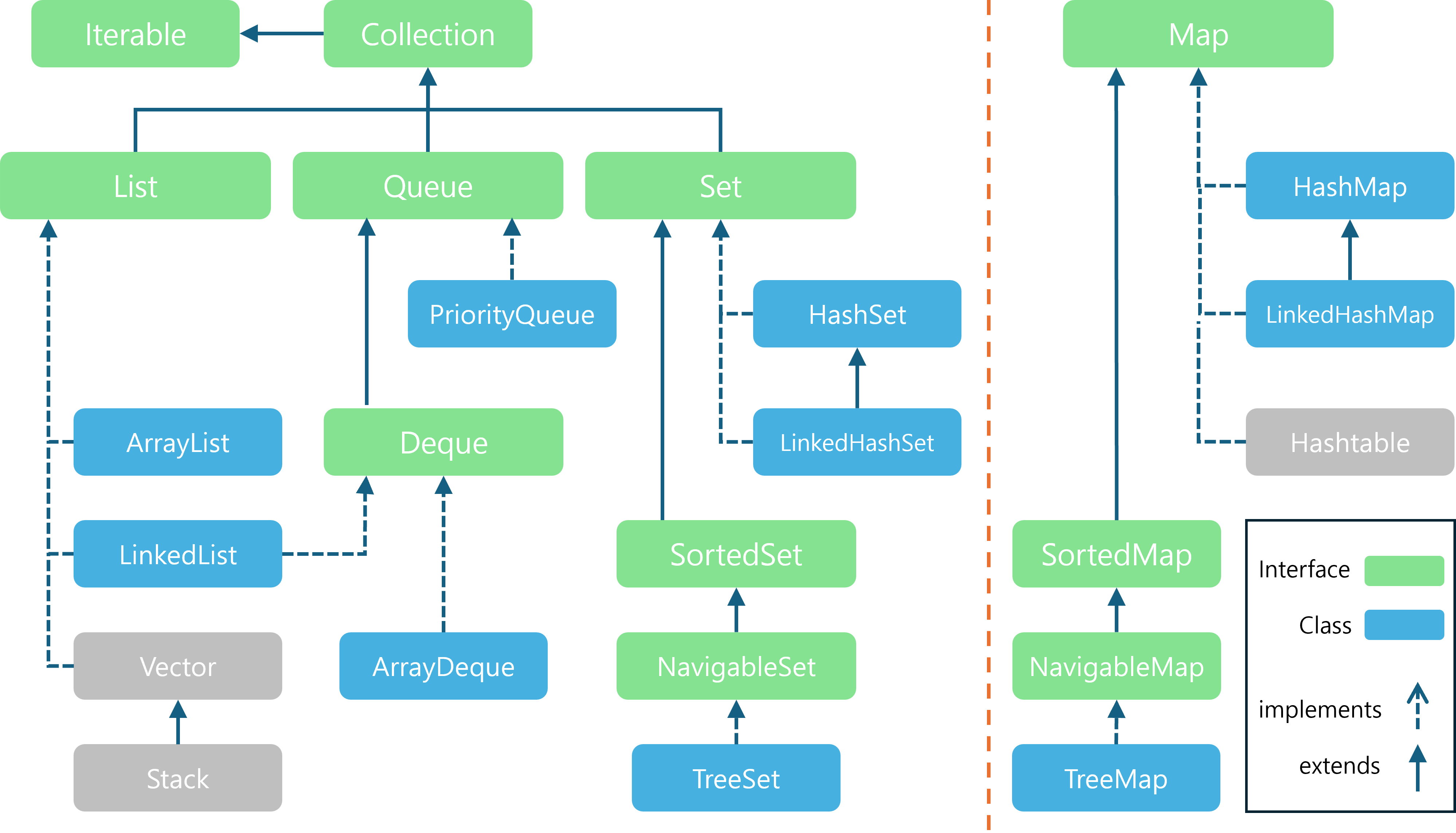
Java에서 제공하는 PriorityQueue는 최소 힙을 기본으로 구현되어 있습니다.

최대 힙을 구현하려면 Comparator를 사용하여 우선순위를 반대로 설정해주어야 합니다.
메서드는 Queue 인터페이스의 메서드들을 활용하시면 됩니다.

3.1.1 최소 힙 구현

import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        // 기본적으로 최소 힙으로 작동
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        minHeap.add(40);
        minHeap.add(10);
        minHeap.add(30);
        minHeap.add(7);

        System.out.println("Min Heap Priority Queue:");
        while (!minHeap.isEmpty()) {
            System.out.print(minHeap.poll() + " ");  // 출력: 7 10 30 40
        }
    }
}

PriorityQueue는 기본적으로 최소 힙으로 작동하며, 값이 작은 것이 우선순위를 가집니다.

3.1.2 최대 힙 구현

최대 힙을 구현하기 위해서는 Comparator를 사용하여 우선순위를 역순으로 설정할 수 있습니다.

import java.util.Collections;
import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        // 최대 힙으로 작동하도록 Comparator 설정
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());

        maxHeap.add(40);
        maxHeap.add(10);
        maxHeap.add(30);
        maxHeap.add(7);

        System.out.println("Max Heap Priority Queue:");
        while (!maxHeap.isEmpty()) {
            System.out.print(maxHeap.poll() + " ");  // 출력: 40 30 10 7
        }
    }
}

Collections.reverseOrder()를 사용하여 최대 힙을 구현할 수 있습니다. 이렇게 하면 값이 큰 것이 우선순위를 가지게 됩니다.
- Comparator.reverseOrder()를 사용하셔도 됩니다. (어차피 같은 객체를 반환합니다)

3.2 Python에서 heapq와 PriorityQueue를 이용한 구현

Python에서는 heapq 모듈과 PriorityQueue 클래스를 사용하여 우선순위 큐를 구현할 수 있습니다. 기본적으로 최소 힙으로 작동하며, 최대 힙을 구현하려면 약간의 트릭이 필요합니다.

3.2.1 최소 힙 구현 (heapq 모듈)

import heapq

# 기본적으로 최소 힙으로 작동
min_heap = []
heapq.heappush(min_heap, 40)
heapq.heappush(min_heap, 10)
heapq.heappush(min_heap, 30)
heapq.heappush(min_heap, 7)

print("Min Heap Priority Queue:")
while min_heap:
    print(heapq.heappop(min_heap), end=' ')  # 출력: 7 10 30 40

heapq.heappush()와 heapq.heappop()을 사용하여 최소 힙 우선순위 큐를 구현할 수 있습니다.

3.2.2 최대 힙 구현 (heapq 모듈)

Python에서 최대 힙을 구현하려면 값을 음수로 변환한 후 heapq를 사용하고, 값을 추출할 때 다시 양수로 변환합니다.

import heapq

# 최대 힙을 구현하기 위해 음수로 값을 변환
max_heap = []
heapq.heappush(max_heap, -40)
heapq.heappush(max_heap, -10)
heapq.heappush(max_heap, -30)
heapq.heappush(max_heap, -7)

print("Max Heap Priority Queue:")
while max_heap:
    print(-heapq.heappop(max_heap), end=' ')  # 출력: 40 30 10 7

음수를 사용하여 우선순위를 반대로 설정하고, 값을 추출할 때 다시 양수로 변환합니다.

3.2.3 PriorityQueue 클래스 사용

queue.PriorityQueue 클래스는 스레드 안전한 방식으로 동작하지만, 기본적으로 최소 힙으로 작동합니다.

from queue import PriorityQueue

pq = PriorityQueue()
pq.put(40)
pq.put(10)
pq.put(30)
pq.put(7)

print("Min Priority Queue (with PriorityQueue):")
while not pq.empty():
    print(pq.get(), end=' ')  # 출력: 7 10 30 40

PriorityQueue는 기본적으로 최소 힙으로 작동하며, get() 메서드를 통해 가장 작은 값을 추출합니다.
최대 힙을 구현할 때는 마찬가지로 값을 음수로 변환한 후, 값을 추출할 때 다시 양수로 변환합니다.

마무리

이번 포스팅에서는 Heap 자료구조와 Priority Queue의 개념, 그리고 이를 Java와 Python에서 어떻게 구현할 수 있는지에 대해 살펴보았습니다.

Heap은 데이터에서 최대값이나 최소값을 빠르게 찾는 데에 유용하며, 특히 우선순위 큐에서 핵심적으로 사용됩니다.
Heap은 그 자체로도 중요한 자료구조지만, 정렬 알고리즘, 그래프 탐색 알고리즘, 작업 스케줄링 등에서 매우 자주 사용되는 도구이기도 합니다.

우선순위 큐는 우선순위가 높은 작업을 먼저 처리해야 하는 상황에서 널리 사용되며, 대표적으로 다음과 같은 분야에서 중요한 역할을 합니다:

작업 스케줄링: 운영체제에서 작업 우선순위를 기준으로 실행 순서를 결정할 때 사용됩니다.
네트워크 패킷 처리: 패킷의 우선순위에 따라 네트워크 트래픽을 관리하고 최적의 경로를 선택하는 데 활용됩니다.
이벤트 기반 시뮬레이션: 이벤트의 발생 시간 순서에 따라 이벤트를 처리해야 할 때 유용하게 쓰입니다.
그래프 알고리즘: 다익스트라 알고리즘과 같은 최단 경로 탐색 문제에서 필수적인 역할을 합니다.
힙 정렬: 정렬 알고리즘 중 하나로, 항상 O(n log n)의 시간 복잡도를 보장하며 효율적으로 데이터를 정렬할 수 있습니다.

다음 포스팅에서는 이진 탐색 트리(Binary Search Tree, BST)를 다루며, 트리 구조를 통해 어떻게 데이터를 효율적으로 관리하고 탐색하는지에 대해 알아보겠습니다.

Kyung Jae, Cheong

일 때문에 포스팅은 잠시 쉬어요 ㅠ 바쁘다 바빠 모두들 화이팅! // Machine Learning (AI) Engineer & BackEnd Engineer (Entry)

이전 포스트

[자료구조] Tree - Binary Tree (이진 트리) - 개념과 구현

다음 포스트