
본 시리즈는 프로그래밍 자료구조의 개념을 정리하고 실습을 진행해보는 시리즈입니다.
- 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
- IDE : IntelliJ IDEA (Ultimate Edition)
- Java : JDK 21 (corretto-21)
- Python : 3.9 (conda env)
트리(Tree) - Red-Black Tree (Part2)
- Red-Black Tree의 개념과 동작원리는 아래 포스팅에서 확인하실 수 있습니다.
4. Java의 Red-Black Tree 클래스 (TreeMap, TreeSet)
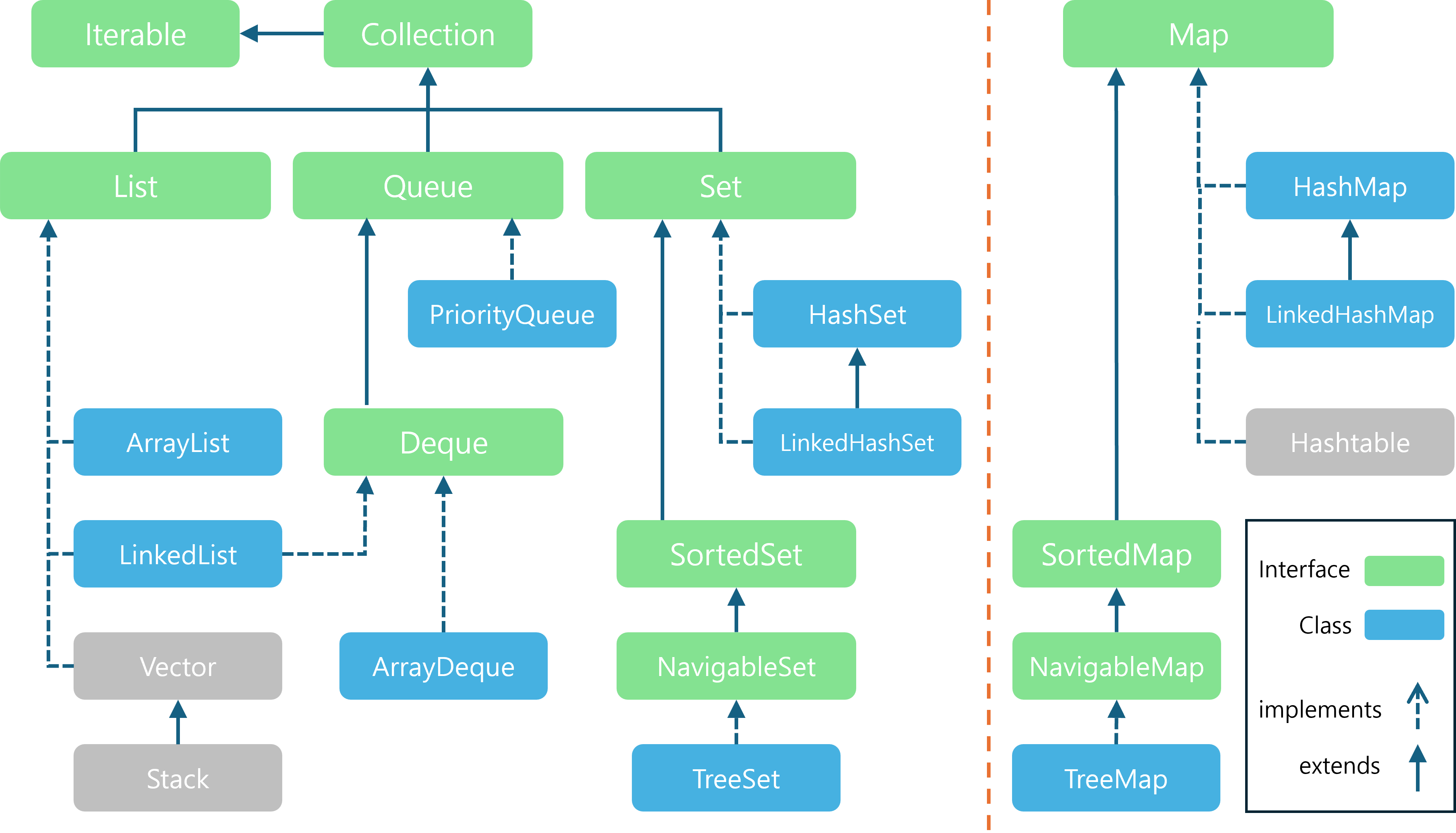
TreeMap과 TreeSet은 Java에서 흔히 사용되는 컬렉션 프레임워크의 클래스들로, 내부적으로 Red-Black Tree를 사용하여 데이터를 저장하고 관리합니다.
- 이러한 자료구조는 데이터를 정렬된 상태로 유지하면서도 삽입, 삭제, 검색 연산이 O(log n)의 시간 복잡도를 보장합니다.
Java의
TreeMap과TreeSet클래스에 대한 자세한 특징과 메서드 목록들은 아래 포스팅에서 확인하실 수 있습니다.
4.1 TreeMap과 TreeSet의 차이점
TreeMap: 키(key)와 값(value)의 쌍으로 데이터를 저장하며, 각 키는 고유한 값을 가집니다.- Map 인터페이스를 구현한 컬렉션으로, 키의 순서에 따라 데이터를 정렬해 저장합니다.
TreeSet: 유일한 값(value) 들을 저장하며, Set 인터페이스를 구현합니다.- 값들이 정렬된 상태로 저장되어 이진 탐색 트리와 같은 성능을 제공합니다.
4.2 TreeMap에서의 Red-Black Tree 활용
TreeMap 클래스는 내부적으로 Red-Black Tree를 사용하여 키-값 쌍을 저장합니다.
- 이는 Map 인터페이스를 구현하면서 동시에 키에 대한 정렬을 유지해야 하기 때문에 Red-Black Tree와 같은 균형 이진 탐색 트리 구조가 적합합니다.
다음은 TreeMap에서 Red-Black Tree가 활용되는 주요 메커니즘입니다:
-
삽입 연산 (
put): 새로운 키-값 쌍을 삽입할 때,TreeMap은 내부적으로 Red-Black Tree의 삽입 규칙에 따라 색상 변경과 회전 연산을 통해 트리의 균형을 유지합니다.put메서드는 새 노드를 추가한 후fixAfterInsertion메서드를 호출하여 삽입 후 트리의 균형을 유지하는 과정이 수행됩니다.
-
삭제 연산 (
remove): 키에 대응하는 값을 삭제할 때에도 Red-Black Tree의 삭제 규칙이 적용됩니다. 노드가 삭제된 후 발생하는 이중 블랙 문제를 해결하기 위해 색상 변경과 회전이 이루어집니다.deleteEntry메서드는 노드를 삭제한 후fixAfterDeletion메서드를 통해 트리의 균형을 맞춥니다.
-
탐색 (Search) :
TreeMap에서는 이진 탐색 트리의 원리에 따라 탐색 연산이 이루어집니다. 키를 기준으로 트리의 왼쪽 또는 오른쪽으로 이동하며, O(log n)의 시간 복잡도를 가집니다.
4.3 TreeSet에서의 Red-Black Tree 활용
TreeSet은 내부적으로 TreeMap을 사용하여 고유한 값을 저장합니다.
- 기본적으로
TreeSet은TreeMap을 활용하여 값을 키로 저장하고, 모든 값이 정렬된 상태로 유지됩니다. TreeMap의 메서드인put,remove등이TreeSet의 삽입 및 삭제 연산에 활용되며, Red-Black Tree의 특성 덕분에 정렬된 데이터에 대해 효율적인 연산이 가능합니다.
Java의
TreeMap과TreeSet클래스에 대한 자세한 특징과 메서드 목록들은 아래 포스팅에서 확인하실 수 있습니다.
TreeMap과 TreeSet은 Red-Black Tree를 활용하여 삽입, 삭제, 탐색 연산을 수행하며, 이를 통해 정렬된 상태를 유지하면서도 O(log n)의 성능을 보장합니다.
이와 같은 자료구조는 실시간 데이터 관리, 정렬된 데이터 조회 등이 필요한 다양한 시스템에서 사용됩니다.
5. Java TreeMap 코드로 Red-Black Tree 동작 원리 분석해보기
이번 섹션에서는 Java의 TreeMap 클래스 내부에서 Red-Black Tree가 어떻게 구현되었는지 주요 메서드를 분석하며 살펴보겠습니다.
TreeMap은 Red-Black Tree를 이용해 키-값 쌍을 정렬된 상태로 저장하며, 이는TreeMap에서 제공하는 삽입, 삭제, 탐색 연산이 O(log n)의 시간 복잡도로 처리될 수 있도록 보장해줍니다.
5.1 필드 변수
TreeMap은 내부적으로 comparator를 사용해 키의 순서를 결정하고, 트리의 루트를 root로, 트리의 크기를 size로 관리합니다.
/**
* The comparator used to maintain order in this tree map, or
* null if it uses the natural ordering of its keys.
*
* @serial
*/
private final Comparator<? super K> comparator;
private transient Entry<K,V> root;
/**
* The number of entries in the tree
*/
private transient int size = 0;
/**
* The number of structural modifications to the tree.
*/
private transient int modCount = 0;comparator: 키의 순서를 결정하는 데 사용됩니다. 만약comparator가null이면 자연 순서(natural ordering)를 따르게 됩니다.root: 트리의 루트를 가리킵니다.size: 트리에 포함된 노드(키-값 쌍)의 개수를 나타냅니다.modCount: 트리의 구조적 변화를 추적하는 변수입니다. 삽입 또는 삭제가 발생할 때마다 증가합니다.
5.1.1 TreeMap의 Enrty 클래스
TreeMap에서 Entry 클래스는 각 노드를 표현하는 중첩 정적 클래스입니다.
- 이 클래스는 Red-Black Tree의 개별 노드를 나타내며, 키-값 쌍을 저장하고, 좌우 자식 노드 및 부모 노드에 대한 참조를 유지합니다.
- 또한, 노드의 색상 정보도 저장하여 Red-Black Tree의 균형을 유지하는 데 기여합니다.
static final class Entry<K,V> implements Map.Entry<K,V> {
K key; // 노드의 키
V value; // 노드의 값
Entry<K,V> left; // 왼쪽 자식 노드
Entry<K,V> right; // 오른쪽 자식 노드
Entry<K,V> parent; // 부모 노드
boolean color = BLACK; // 노드의 색상 (RED 또는 BLACK)
/**
* 새로운 노드를 생성할 때 키, 값, 부모 노드를 설정하고
* 자식 노드들은 null로 설정, 색상은 기본적으로 BLACK으로 설정
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key; // 키 설정
this.value = value; // 값 설정
this.parent = parent; // 부모 노드 설정
}
}
// Red-black mechanics
private static final boolean RED = false;
private static final boolean BLACK = true;주요 필드 설명:
key: 노드가 저장하는 키입니다.TreeMap은 키를 기준으로 노드를 정렬하고 관리합니다.value: 노드가 저장하는 값입니다. 각 노드는 키와 값을 쌍으로 저장하며, 키를 기준으로 값에 접근할 수 있습니다.left: 노드의 왼쪽 자식 노드를 가리키는 참조입니다.right: 노드의 오른쪽 자식 노드를 가리키는 참조입니다.parent: 부모 노드를 가리키는 참조로, 트리에서 각 노드의 부모 관계를 추적하는 데 사용됩니다.color: 노드의 색상 정보로, Red-Black Tree의 규칙을 유지하기 위해 RED 또는 BLACK 값을 가집니다.- BLACK은
true, RED는false인 boolean 타입의 변수입니다. - 새로 생성된 노드는 기본적으로 BLACK으로 설정됩니다.
- BLACK은
5.2 탐색 (getEntry)
getEntry 메서드는 주어진 키에 대해 TreeMap에서 해당 노드(Entry)를 탐색하는 메서드입니다.
- 이 메서드는 이진 탐색 트리의 원리를 따르며, 각 노드의 키와 비교해 왼쪽 또는 오른쪽 서브트리로 이동하며 탐색을 진행합니다.
/**
* Returns this map's entry for the given key, or {@code null} if the map
* does not contain an entry for the key.
*
* @return this map's entry for the given key, or {@code null} if the map
* does not contain an entry for the key
* @throws ClassCastException if the specified key cannot be compared
* with the keys currently in the map
* @throws NullPointerException if the specified key is null
* and this map uses natural ordering, or its comparator
* does not permit null keys
*/
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key); // Comparator를 사용하는 경우
if (key == null)
throw new NullPointerException(); // null 키는 허용되지 않음
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key); // 현재 노드의 키와 비교
if (cmp < 0)
p = p.left; // 왼쪽으로 이동
else if (cmp > 0)
p = p.right; // 오른쪽으로 이동
else
return p; // 일치하는 키 발견
}
return null; // 해당 키를 찾지 못한 경우 null 반환
}이 메서드는 이진 탐색 트리의 원리를 따르며, 각 노드의 키를 비교해 왼쪽 또는 오른쪽 자식으로 이동하며 탐색을 진행합니다.
comparator가 있으면 이를 이용해 키를 비교하고, 없으면 기본적으로Comparable인터페이스를 구현한 키의 자연 순서를 따릅니다.
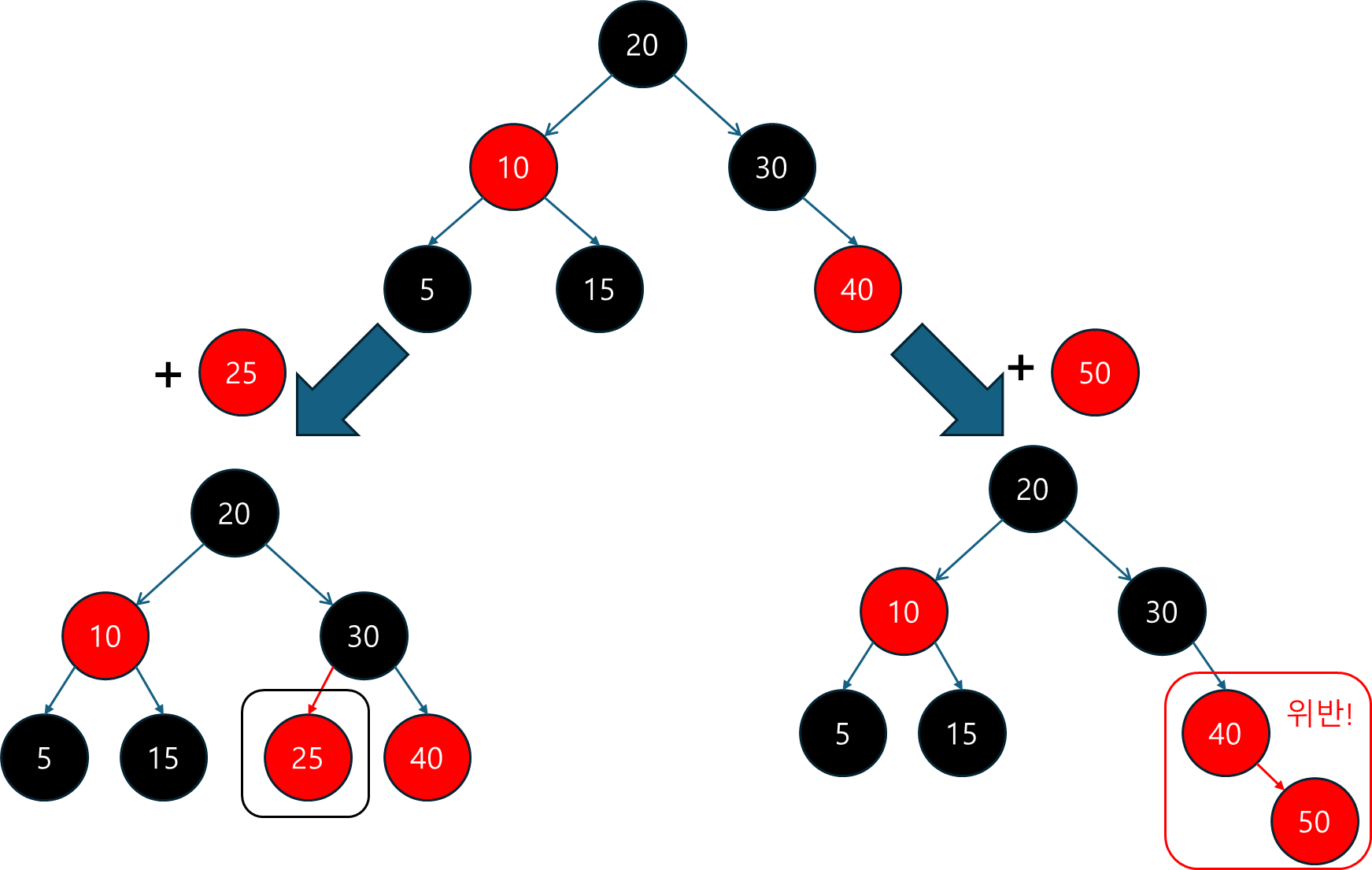
5.3 삽입 연산 (put)
put 메서드는 새로운 키-값 쌍을 삽입하는 메서드입니다.
- 이 메서드는 트리에서 해당 키의 위치를 찾아 삽입하고, 만약 이미 같은 키가 존재한다면 기존 값을 새로운 값으로 대체합니다.
- 삽입 후 트리의 균형을 유지하기 위해 색상 변경과 회전 연산이 이루어집니다.
/**
* Associates the specified value with the specified key in this map.
* If the map previously contained a mapping for the key, the old
* value is replaced.
*
* @param key key with which the specified value is to be associated
* @param value value to be associated with the specified key
*
* @return the previous value associated with {@code key}, or
* {@code null} if there was no mapping for {@code key}.
* (A {@code null} return can also indicate that the map
* previously associated {@code null} with {@code key}.)
* @throws ClassCastException if the specified key cannot be compared
* with the keys currently in the map
* @throws NullPointerException if the specified key is null
* and this map uses natural ordering, or its comparator
* does not permit null keys
*/
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) { // 트리가 비어있다면 루트 노드를 삽입
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) { // Comparator를 사용하는 경우
do {
parent = t;
cmp = cpr.compare(key, t.key); // 키 비교
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else // 같은 키가 이미 존재하는 경우 값 대체
return t.setValue(value);
} while (t != null);
}
else { // Comparator가 없는 경우
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else // 같은 키가 이미 존재하는 경우 값 대체
return t.setValue(value);
} while (t != null);
}
// 새로운 노드를 부모 노드에 연결
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e); // 삽입 후 트리 균형 유지 (색상 변경 및 회전)
size++;
modCount++;
return null;
}주요 처리 과정:
-
트리 탐색: 루트부터 시작해, 새로운 키가 들어갈 자리를 찾습니다. 비교 기준은
comparator또는 키의 자연 순서에 따릅니다. -
노드 삽입: 삽입할 자리를 찾으면 새로운 노드를 생성하고 부모 노드에 연결합니다.
-
트리 균형 유지:
fixAfterInsertion메서드를 호출하여 삽입 후 발생할 수 있는 트리 불균형을 해결합니다. 이는 Red-Black Tree의 삽입 규칙을 따르며, 색상 변경과 회전 연산을 통해 트리의 균형을 유지합니다.
이와 같이 TreeMap에서의 삽입은 이진 탐색 트리처럼 이루어지지만, 삽입 후 Red-Black Tree의 특성을 유지하기 위해 추가적인 작업(색상 변경, 회전)이 필요합니다.
5.3.1 삽입 후 균형 유지를 위한 static 변수 및 메서드
Red-Black Tree에서 삽입 연산 후 트리의 균형을 유지하기 위해서는 색상 변경과 회전이 필수적입니다. 이를 지원하기 위해 TreeMap에서는 몇 가지 static 변수와 유틸리티 메서드가 정의되어 있습니다.
// Red-black mechanics
private static final boolean RED = false;
private static final boolean BLACK = true;
// Balancing operations.
private static <K,V> boolean colorOf(Entry<K,V> p) {
return (p == null ? BLACK : p.color); // null 노드는 항상 BLACK으로 처리
}
private static <K,V> Entry<K,V> parentOf(Entry<K,V> p) {
return (p == null ? null: p.parent); // 부모 노드를 반환
}
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c; // 노드의 색상을 설정
}
private static <K,V> Entry<K,V> leftOf(Entry<K,V> p) {
return (p == null) ? null: p.left; // 왼쪽 자식 노드를 반환
}
private static <K,V> Entry<K,V> rightOf(Entry<K,V> p) {
return (p == null) ? null: p.right; // 오른쪽 자식 노드를 반환
}
주요 메서드 설명:
colorOf: 노드의 색상을 반환합니다. 만약 노드가null이라면 해당 노드를 BLACK으로 간주합니다.setColor: 주어진 노드의 색상을 설정합니다.parentOf: 부모 노드를 반환하는 메서드입니다.leftOf및rightOf: 각각 주어진 노드의 왼쪽 또는 오른쪽 자식 노드를 반환합니다.
이와 같은 메서드들은 트리의 균형을 맞추기 위해 색상과 노드 위치를 제어할 때 사용됩니다.
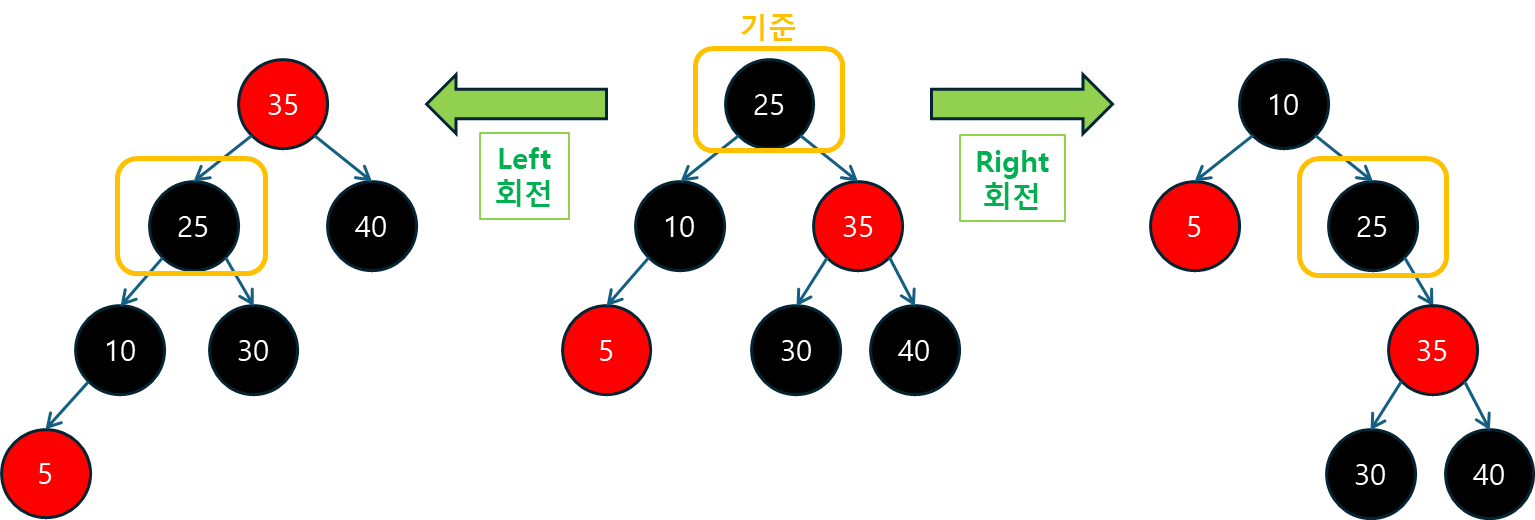
5.3.2 회전 연산 메서드 (rotateLeft, rotateRight)
회전 연산은 Red-Black Tree에서 트리의 균형을 맞추는 중요한 연산입니다. TreeMap에서는 좌회전과 우회전을 수행하는 두 개의 메서드가 존재합니다.
/** From CLR */
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right; // r : p의 오른쪽 자식
p.right = r.left; // r의 왼쪽 자식을 p의 오른쪽 자식으로
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null) // p가 루트인 경우
root = r; // r을 새로운 루트로 설정
else if (p.parent.left == p)
p.parent.left = r; // p가 부모의 왼쪽 자식인 경우
else
p.parent.right = r; // p가 부모의 오른쪽 자식인 경우
r.left = p; // r의 왼쪽 자식으로 p 설정
p.parent = r;
}
}
/** From CLR */
private void rotateRight(Entry<K,V> p) { //rotateLeft의 방향만 반대로
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}좌회전과 우회전은 트리의 구조를 바꾸어 트리의 높이를 줄이고 균형을 유지하기 위한 방법입니다.
- 삽입 또는 삭제 연산 후 트리의 규칙을 깨뜨릴 수 있는 불균형이 발생할 때, 이 회전 연산을 통해 균형을 복구합니다.
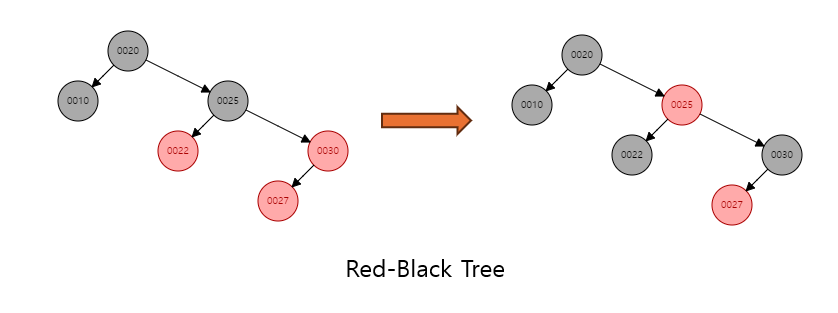
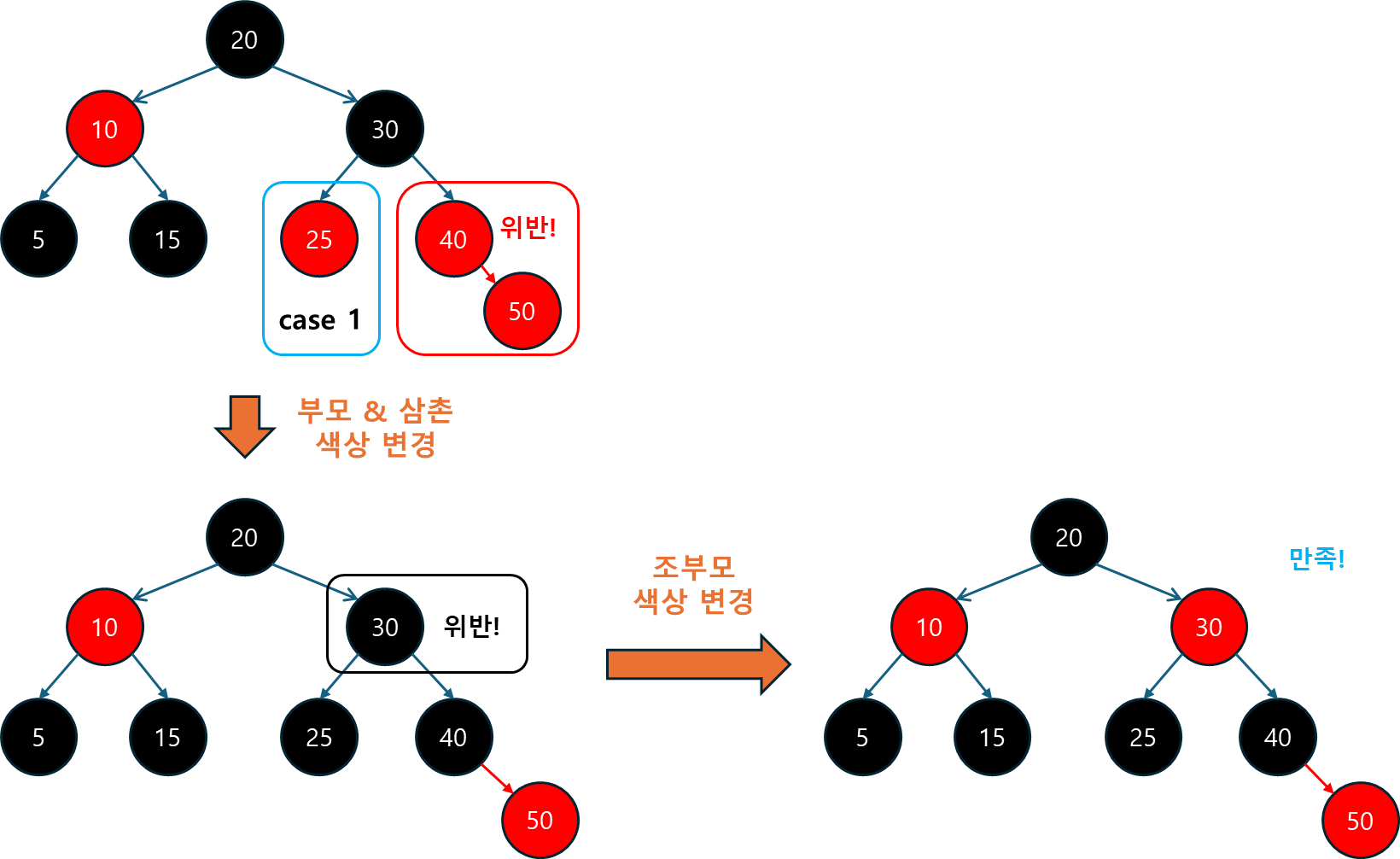
5.3.3 삽입 후 균형 맞추기 (fixAfterInsertion)
fixAfterInsertion 메서드는 Red-Black Tree의 규칙을 유지하기 위해 삽입 후 발생할 수 있는 불균형을 회전과 색상 변경을 통해 해결하는 메서드입니다.
- 새로 삽입된 노드는 항상 RED로 설정되며, 이를 기반으로 트리의 규칙을 확인하고 적절히 조정합니다.
/** From CLR */
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; // 새로 삽입된 노드는 항상 RED
// 부모가 RED인 경우 불균형 발생
while (x != null && x != root && x.parent.color == RED) {
// 부모가 조부모의 왼쪽 자식인 경우
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 삼촌 노드
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// Case 1: 삼촌 노드가 RED인 경우
if (colorOf(y) == RED) {
// 부모와 삼촌을 BLACK으로
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
// 조부모를 RED로 변경
setColor(parentOf(parentOf(x)), RED);
// 조부모로 이동해 반복 (전파)
x = parentOf(parentOf(x));
} else { // Case 2: 삼촌이 BLACK인 경우
// 삽입된 노드가 오른쪽 자식일 경우
if (x == rightOf(parentOf(x))) {
x = parentOf(x); // x를 부모로 이동 (회전 후 자식이 됨)
rotateLeft(x); // 왼쪽 회전
}
// 부모를 BLACK, 조부모를 RED로 색상 변경
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
// 조부모 기준 오른쪽 회전
rotateRight(parentOf(parentOf(x)));
}
} else { // 부모가 오른쪽 자식인 경우 (대칭 처리)
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK; // 루트는 항상 BLACK으로 유지
}핵심 처리 과정:
-
삼촌 노드가 RED인 경우: 부모와 삼촌을 BLACK으로, 조부모를 RED로 변경하고 조부모를 기준으로 다시 균형을 확인합니다.
-
삼촌 노드가 BLACK인 경우: 삼촌이 BLACK일 때, 삽입된 노드가 부모의 왼쪽 자식인지 오른쪽 자식인지에 따라 회전을 수행하고, 색상을 적절히 변경하여 균형을 맞춥니다.
-
루트 노드는 항상 BLACK: 마지막으로 루트는 항상 BLACK으로 유지되어야 하므로, 모든 처리가 끝난 후 루트의 색상을 BLACK으로 설정합니다.
이처럼 삽입 후 발생할 수 있는 불균형을 색상 변경과 회전으로 해결하여 Red-Black Tree의 균형을 유지합니다.
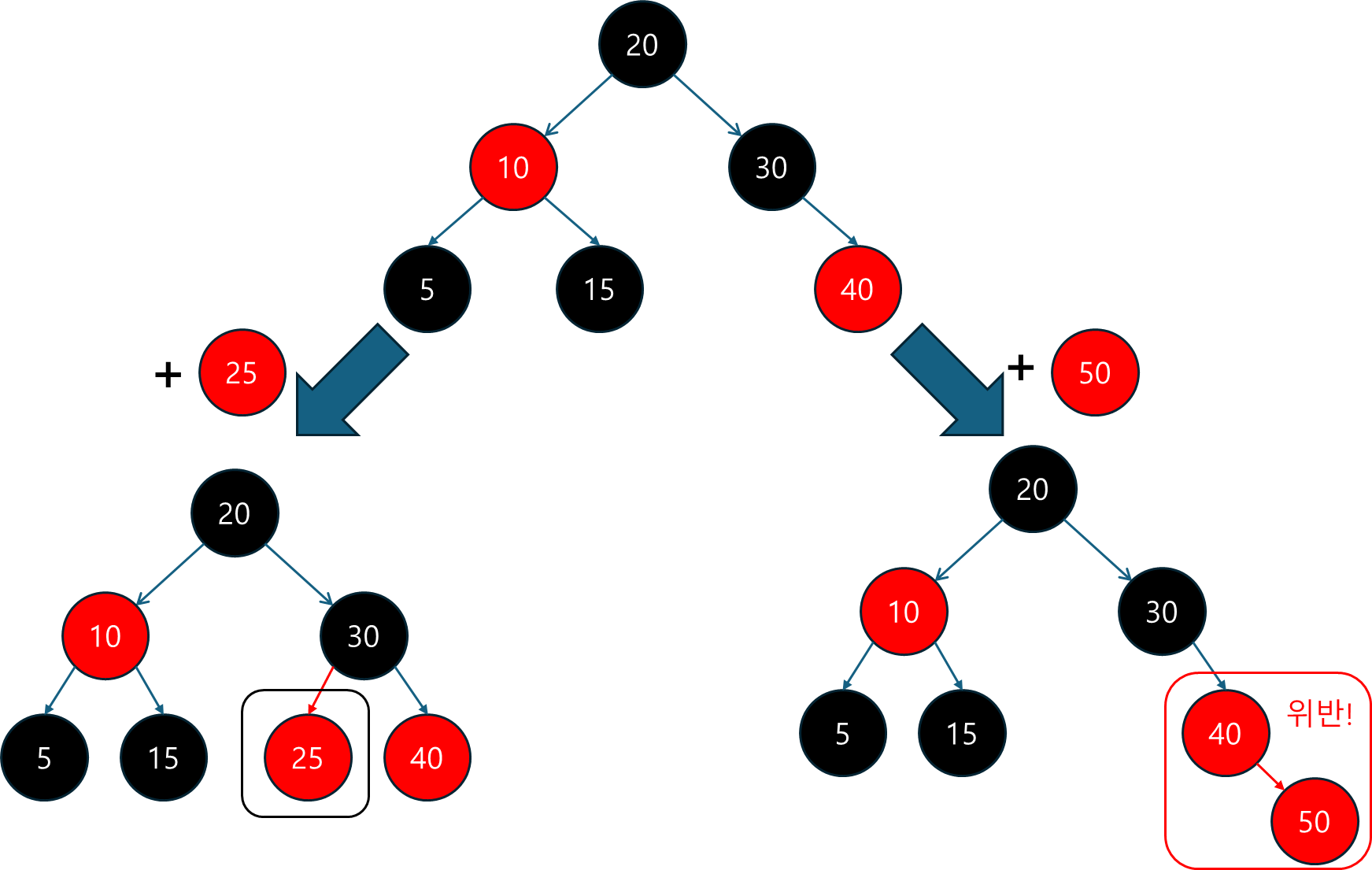
| 경우 | 부모 노드 색상 | 형제(삼촌) 노드 색상 | 해결 방법 |
|---|---|---|---|
| Case 1 | 레드 (Red) | 레드 (Red) | 색상 변경: 부모와 형제를 블랙으로, 조부모를 레드로 변경. 조부모가 루트가 아닐 경우 상위 노드로 색상 위반 문제 전파 |
| Case 2-1 (단일 회전) | 레드 (Red) | 블랙 (Black) 혹은 NIL | 단일 회전: 부모와 삽입된 노드가 조부모와 같은 방향에 있을 경우 단일 회전(LL 또는 RR)으로 재구조화 실시 |
| Case 2-2 (이중 회전) | 레드 (Red) | 블랙 (Black) 혹은 NIL | 이중 회전: 부모와 삽입된 노드가 조부모와 반대 방향에 있을 경우 이중 회전(LR 또는 RL)으로 재구조화 실시 |
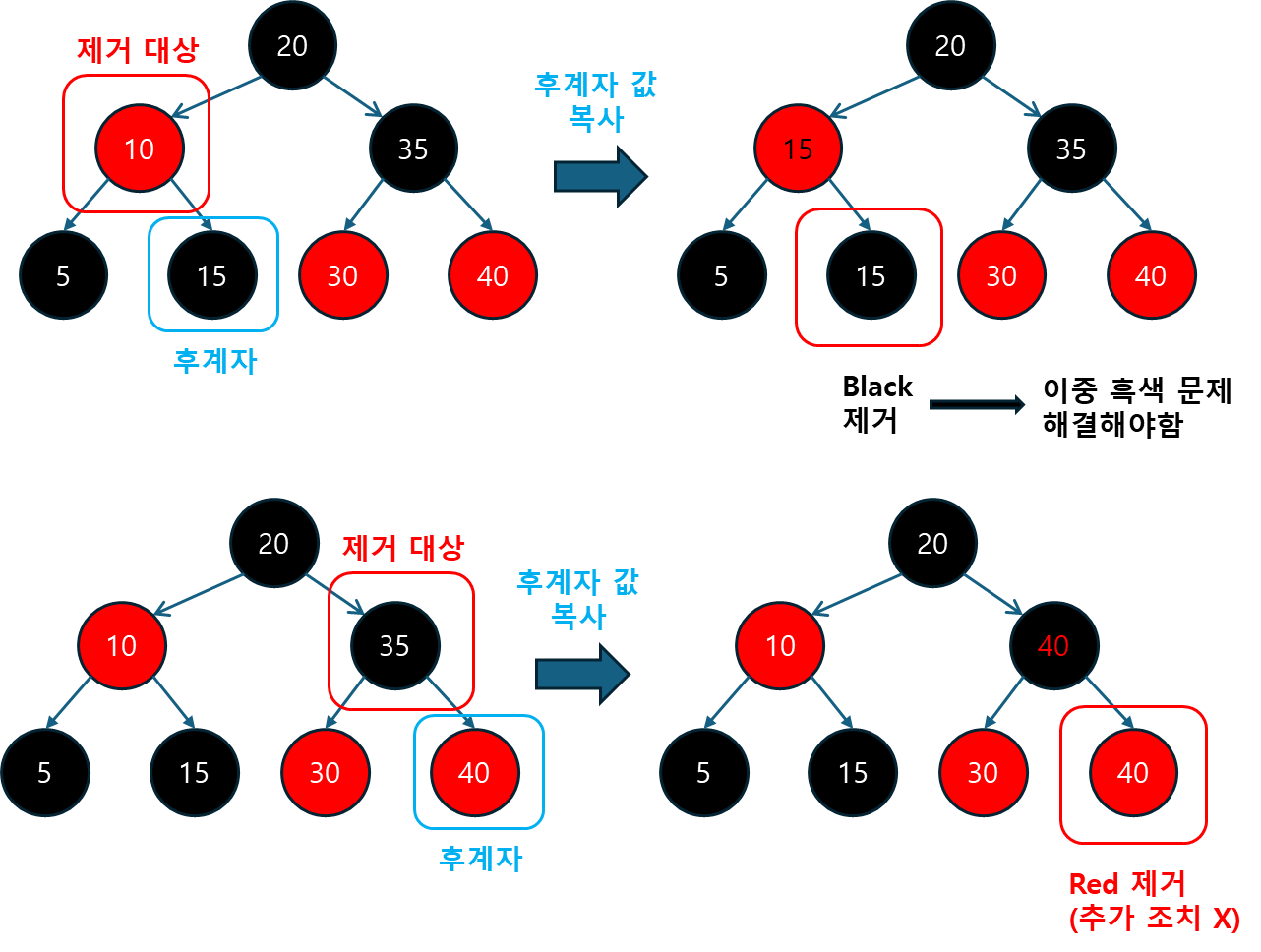
5.4 삭제 연산 (remove)
remove 메서드는 주어진 키에 해당하는 노드를 삭제하는 역할을 합니다.
- 이 메서드는 먼저 탐색을 통해 삭제할 노드를 찾고, 이후 해당 노드를 삭제하는 작업을 수행합니다.
- 이때 BLACK 노드가 삭제된 경우에는 Red-Black Tree의 균형을 맞추기 위한 후처리가 이루어지게 됩니다.
public V remove(Object key) {
Entry<K,V> p = getEntry(key); // 주어진 키에 해당하는 노드를 탐색
if (p == null)
return null; // 노드를 찾지 못하면 null 반환
V oldValue = p.value; // 기존 값 저장
deleteEntry(p); // 노드를 삭제
return oldValue; // 삭제된 노드의 값을 반환
}remove 메서드는 다음과 같은 단계로 작동합니다:
- 탐색: 먼저,
getEntry메서드를 사용하여 삭제할 노드를 찾습니다. 만약 노드가 없다면null을 반환합니다. - 삭제: 노드를 찾으면, 해당 노드의 값을 저장하고,
deleteEntry메서드를 호출하여 노드를 삭제합니다. - 값 반환: 삭제된 노드의 값을 반환합니다.
5.4.1 후계자를 찾는 static 메서드 (successor)
successor 메서드는 삭제 연산 중 후계자 노드(즉, 삭제된 노드를 대체할 노드)를 찾기 위해 사용됩니다.
- 일반적으로 삭제할 노드가 두 자식을 가지고 있을 경우, 그 후계자는 오른쪽 서브트리에서 가장 작은 노드가 됩니다.
/**
* Returns the successor of the specified Entry, or null if no such.
*/
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) { // 오른쪽 자식이 있으면 오른쪽 서브트리에서 후계자 찾기
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left; // 오른쪽 서브트리에서 가장 작은 노드 탐색
return p;
} else { // 오른쪽 자식이 없을 경우, 부모 노드로 올라가서 후계자 찾기
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
// 부모 노드가 오른쪽 자식인 동안 상위 노드로 올라감
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p; // 후계자를 반환
}
}successor 메서드의 동작:
- 오른쪽 서브트리에서 후계자 탐색: 만약 노드의 오른쪽 자식이 존재한다면, 오른쪽 서브트리에서 가장 작은 값을 가진 노드가 후계자가 됩니다.
- 즉, 오른쪽 서브트리의 가장 왼쪽 노드가 후계자입니다.
- 부모 노드로 이동: 만약 오른쪽 자식이 없다면, 부모 노드로 이동하여 후계자를 찾습니다.
- 부모로 올라가면서, 노드가 부모의 오른쪽 자식이 아닐 때까지 계속 부모로 이동합니다.
이 후계자 찾기 로직은 Red-Black Tree에서 삭제 연산이 일어날 때 중요한 역할을 합니다. 삭제할 노드가 두 자식을 가지고 있을 경우, 후계자 노드로 값을 대체한 후, 그 후계자를 삭제하는 방식으로 처리됩니다.
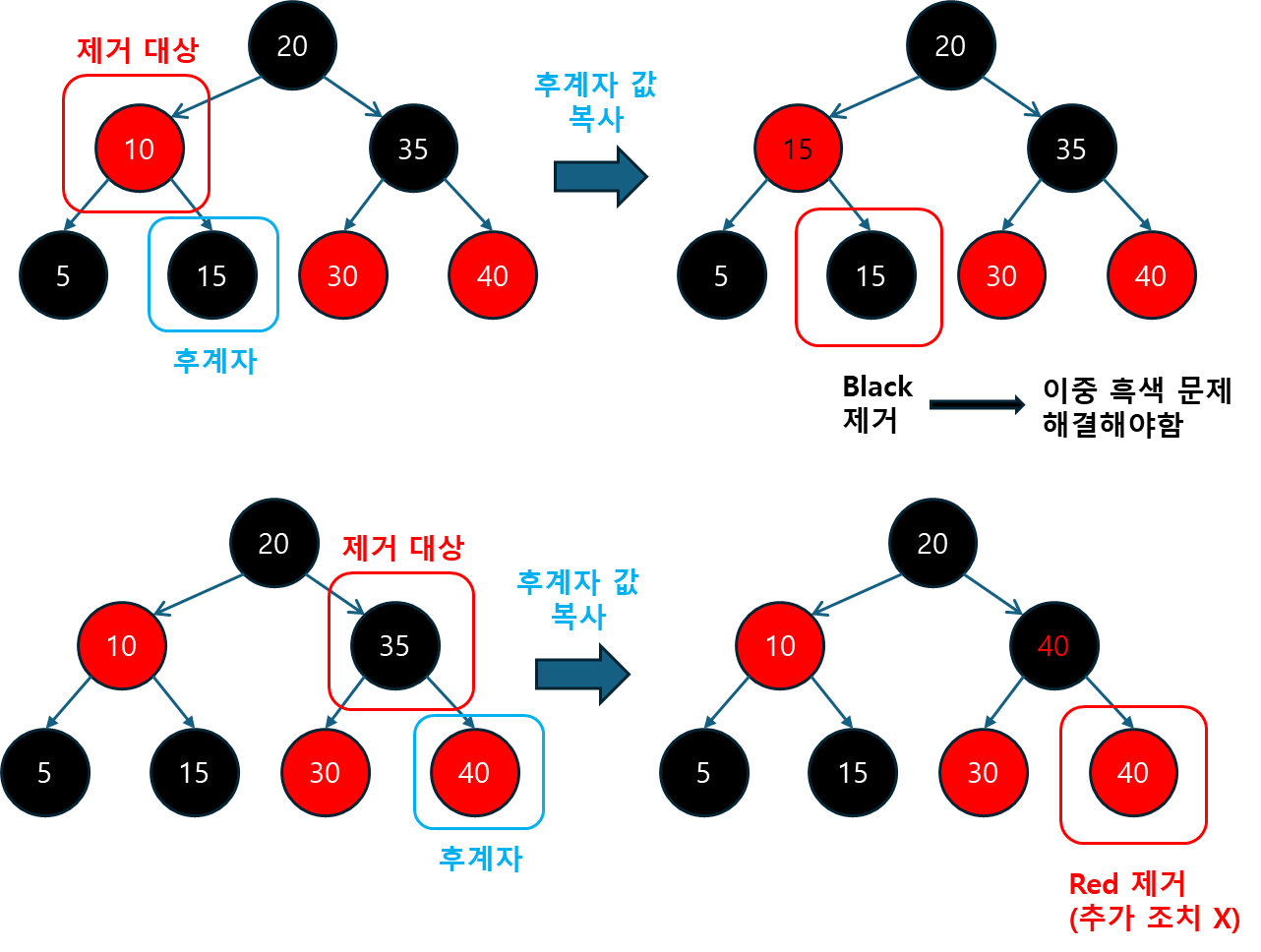
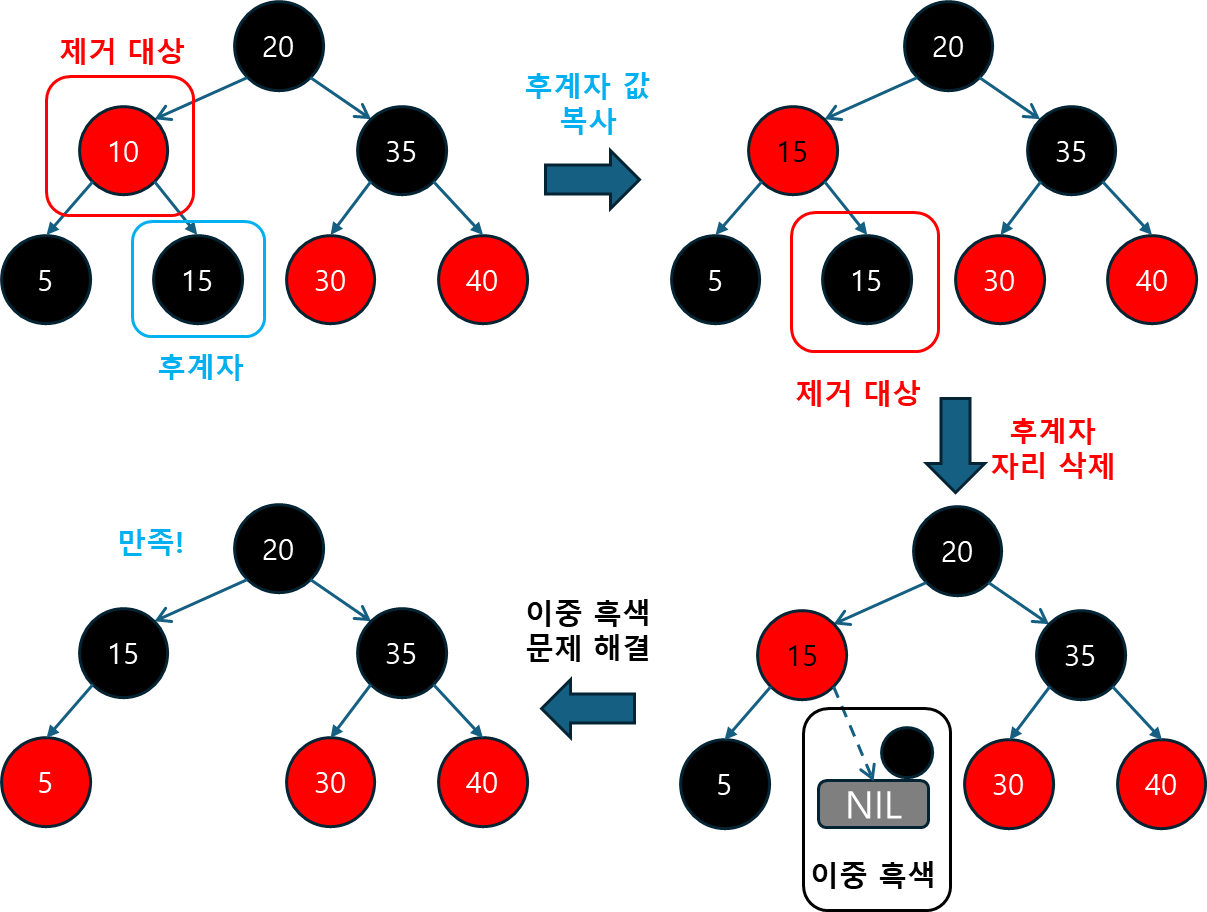
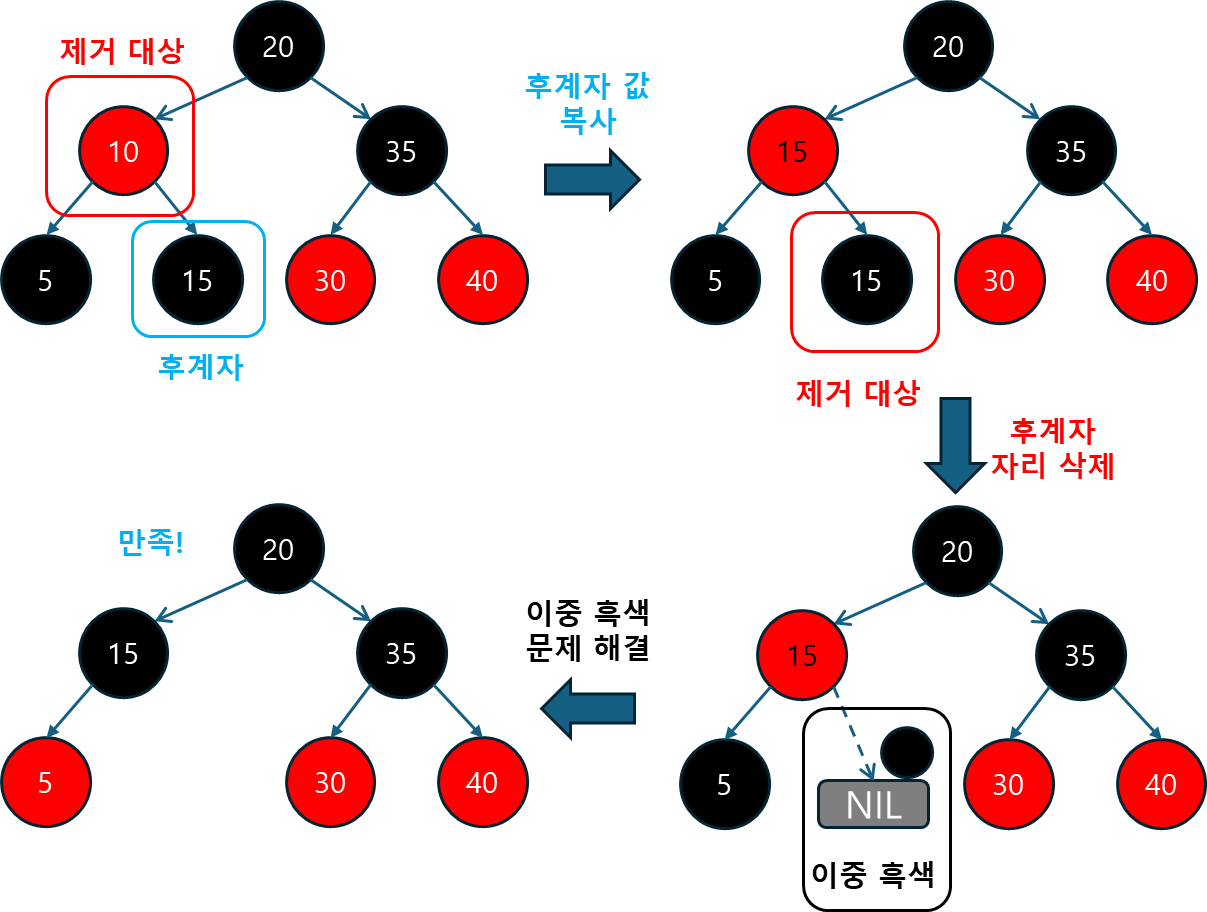
5.4.2 Entry를 삭제하는 메서드 (deleteEntry)
deleteEntry 메서드는 노드를 삭제하고, 트리의 균형을 복구하는 역할을 합니다.
- 노드가 삭제된 후, 이중 블랙 문제가 발생할 수 있으므로, 이를 해결하기 위한 후처리 작업이 필요합니다.
/**
* Delete node p, and then rebalance the tree.
*/
private void deleteEntry(Entry<K,V> p) {
modCount++; // 트리 구조 변경 횟수 증가
size--; // 트리 크기 감소
// 노드가 두 자식을 가지고 있는 경우 후계자의 값을 복사하고 후계자를 삭제
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p); // 후계자를 찾음
p.key = s.key; // 후계자의 키 복사
p.value = s.value; // 후계자의 값 복사
p = s; // 후계자를 실제로 삭제할 노드로 설정
} // p has 2 children
// 자식이 하나만 있는 경우 해당 자식을 대체할 노드로 설정
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
// 대체 노드를 부모 노드와 연결
replacement.parent = p.parent;
// 삭제한 노드가 루트일 경우 대체 노드를 루트로 설정
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
// 연결이 해제된 노드의 참조를 null로 설정
p.left = p.right = p.parent = null;
// Fix replacement
// 삭제한 노드가 블랙일 경우, 트리의 균형을 복구
if (p.color == BLACK)
fixAfterDeletion(replacement);
// 삭제한 노드가 루트이면서 자식이 없는 경우
} else if (p.parent == null) { // return if we are the only node.
root = null; // 트리를 비움
// 자식이 없는 리프 노드인 경우
} else { // No children. Use self as phantom replacement and unlink.
// 삭제한 노드가 블랙일 경우 균형 복구
if (p.color == BLACK)
fixAfterDeletion(p);
// 부모 노드에서 삭제된 노드를 제거
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
deleteEntry의 주요 동작:
- 노드가 두 자식을 가진 경우: 후계자 노드(오른쪽 서브트리에서 가장 작은 노드)의 값을 삭제할 노드에 복사하고, 후계자 노드를 실제로 삭제합니다.
- 자식이 하나만 있는 경우: 자식 노드를 삭제할 노드의 위치로 대체합니다.
- 균형 복구: 삭제된 노드가 블랙일 경우
fixAfterDeletion메서드를 호출하여 트리의 균형을 맞춥니다. 이때 이중 블랙 문제를 해결하는 과정이 수행 됩니다. - 자식이 없는 리프 노드인 경우: 부모와의 연결을 끊고, 트리의 균형을 복구합니다.
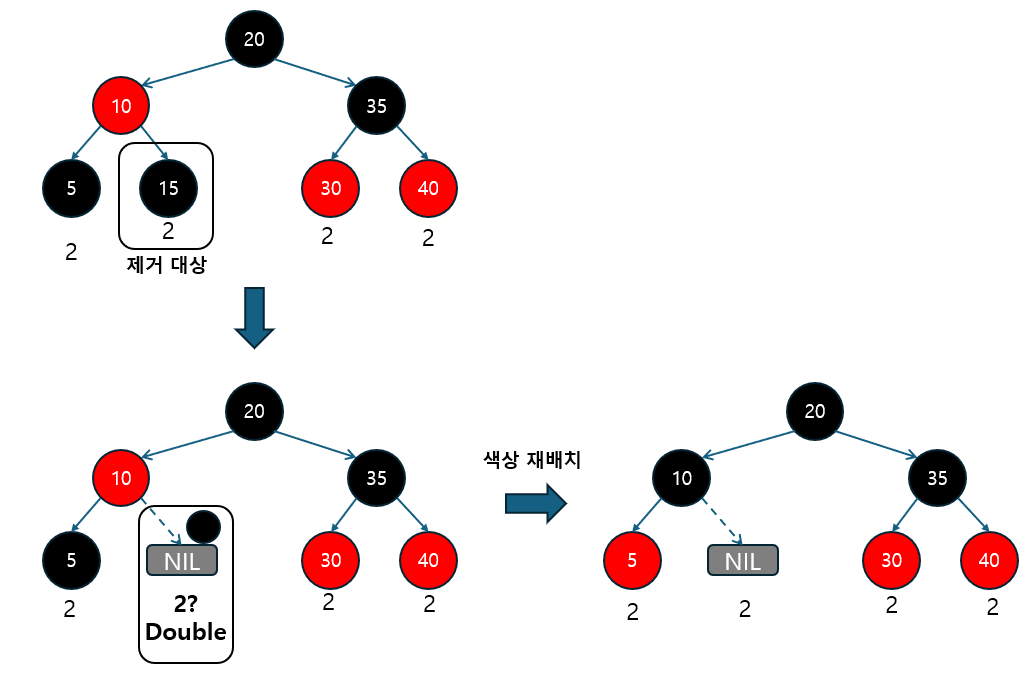
5.4.3 삭제 후 이중 블랙 문제를 해결하는 메서드 (fixAfterDeletion)
fixAfterDeletion 메서드는 노드 삭제 후 발생할 수 있는 이중 블랙 문제를 해결하는 역할을 합니다.
- 이중 블랙 문제는 Red-Black Tree의 규칙을 위반하는 상태로, 이를 해결하기 위해 색상 변경과 회전 연산이 사용됩니다.
/** From CLR */
private void fixAfterDeletion(Entry<K,V> x) {
// 해결 대상 노드가 루트가 아니면서 BLACK인 경우 반복
while (x != root && colorOf(x) == BLACK) {
// 해결 대상 노드가 부모의 왼쪽 노드인 경우
if (x == leftOf(parentOf(x))) {
// 형제 노드 찾기 (없으면 NIL 노드)
Entry<K,V> sib = rightOf(parentOf(x));
// Case 1 : 형제가 RED인 경우
if (colorOf(sib) == RED) {
setColor(sib, BLACK); // 형제를 BLACK으로 변경
setColor(parentOf(x), RED); // 부모를 RED로 변경
rotateLeft(parentOf(x)); // 부모 기준 좌회전
sib = rightOf(parentOf(x)); // 회전후 새로운 형제 노드 설정
}
// Case 2 : 형제가 BLACK이고, 조카노드들이 모두 BLACK인 경우
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED); // 형제를 레드로 변경
x = parentOf(x); // 이중 블랙 문제를 상위 노드로 전파
}
// Case 3 : 형제가 BLACK이고, 조카노드 중 하나 이상이 RED인 경우
else {
// Case 3-1 : 형제(Right)과 반대 방향(Left)에 RED조카가 있는 경우
if (colorOf(rightOf(sib)) == BLACK) {
// 왼쪽 RED 조카를 BLACK으로, 형제 노드를 RED로 변경
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
// 형제 기준 우회전
rotateRight(sib);
sib = rightOf(parentOf(x)); // 새로운 형제 노드 설정
}
// Case 3-2 : 형제(Right)과 같은 방향(Right)에 RED조카가 있는 경우
setColor(sib, colorOf(parentOf(x))); // 형제의 색상을 부모의 색상으로 설정
setColor(parentOf(x), BLACK); // 부모를 블랙으로 변경
setColor(rightOf(sib), BLACK); // 형제의 오른쪽 자식을 블랙으로 변경
rotateLeft(parentOf(x)); // 부모 기준 좌회전
x = root; // 문제 해결 후 루트로 설정하여 반복 종료
}
} else { // symmetric (좌우 대칭)
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
// 최종적으로 이중 블랙 문제 해결 후, 해당 노드를 블랙으로 설정
setColor(x, BLACK);
}fixAfterDeletion의 동작 과정:
-
이중 블랙 문제 해결: 삭제된 노드로 인해 발생한 이중 블랙 문제를 해결하기 위해 형제 노드와 그 자식(조카)들의 색상을 확인합니다.
-
Case 1) 형제가 레드인 경우: 형제의 색상을 블랙으로 바꾸고, 부모를 레드로 변경한 후 회전을 수행합니다.
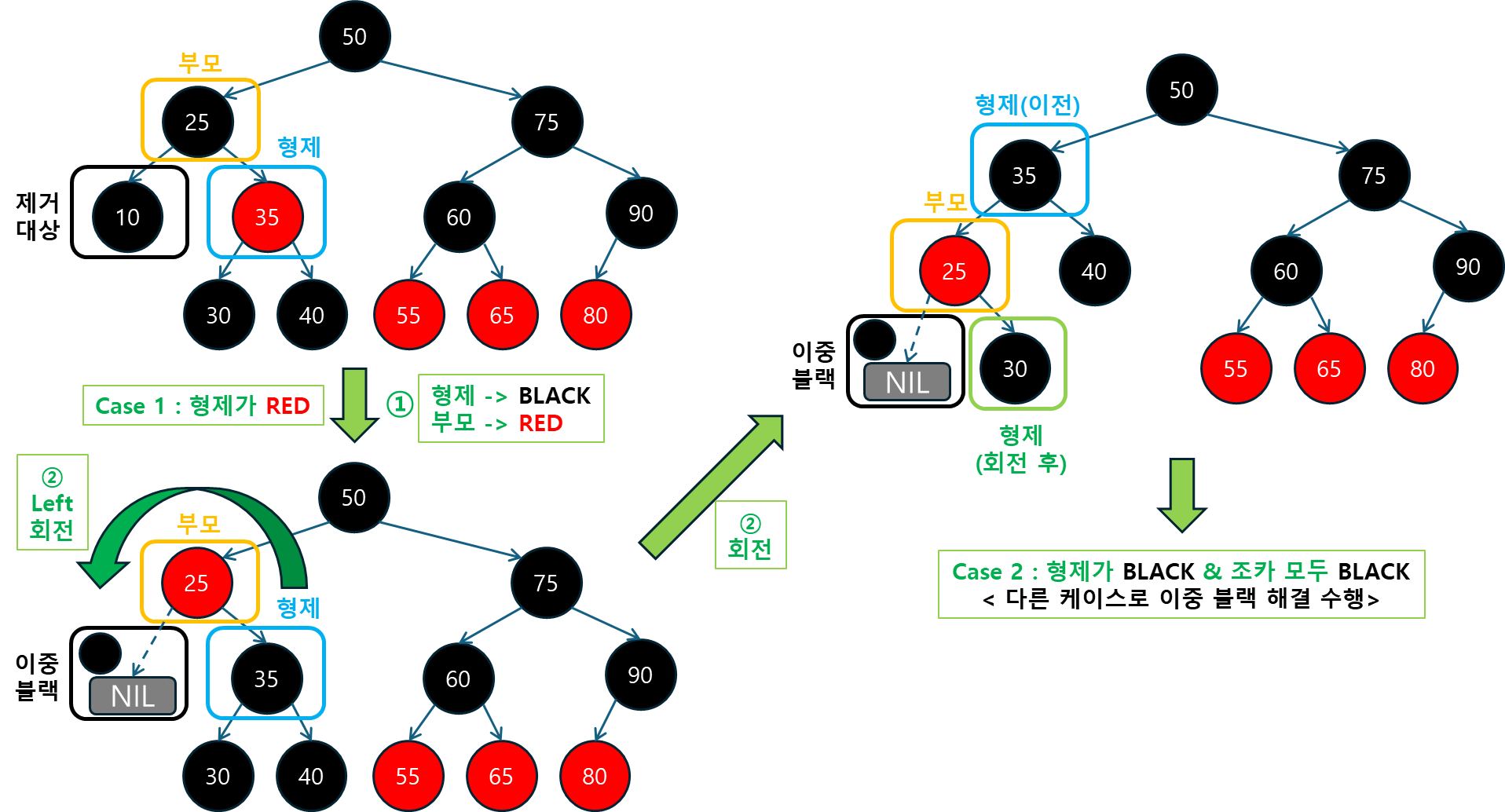
-
Case 2) 형제와 그 자식(조카)들이 모두 블랙인 경우: 형제를 레드로 바꾸고 이중 블랙 문제를 상위 노드로 전파합니다.
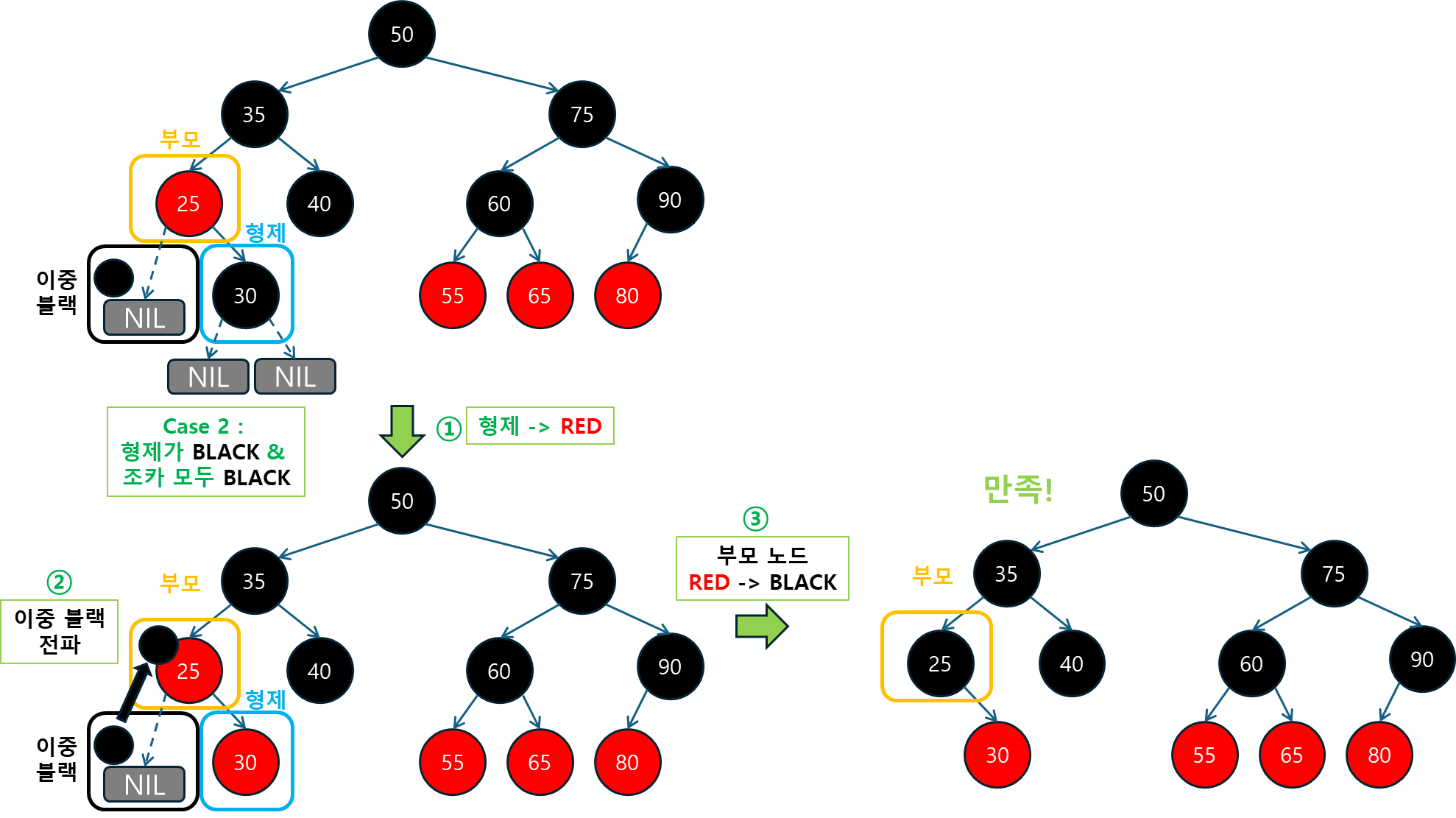
-
Case 3) 형제의 자식(조카) 중 하나 이상 레드인 경우: 색상을 적절히 변경한 후 회전을 통해 문제를 해결합니다.
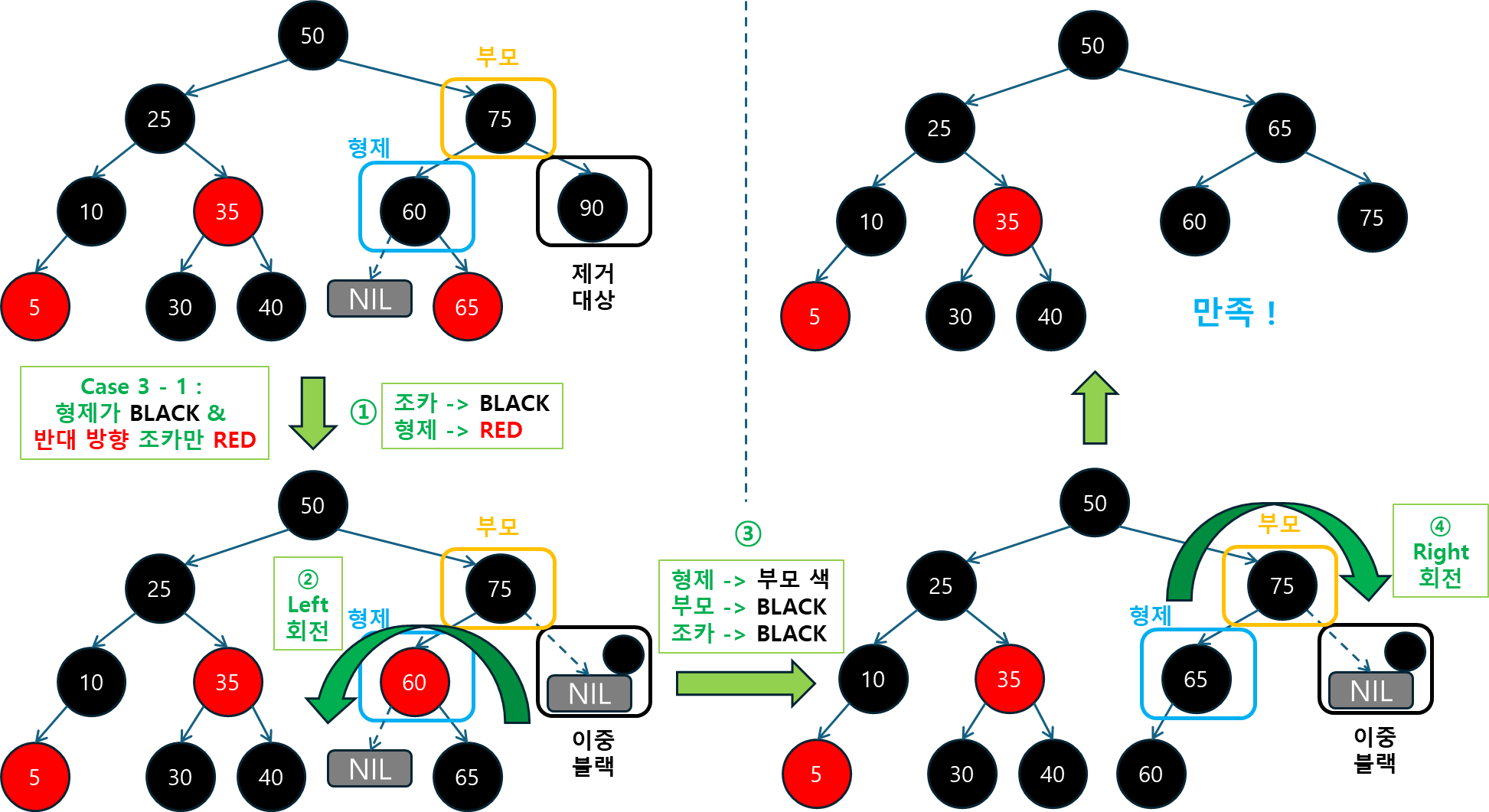
-
| 경우 | 형제 노드 색상 | 조카 노드 상태 | 해결 방법 |
|---|---|---|---|
| Case 1 | 레드 (Red) | 상관없음 | 형제를 블랙으로, 부모를 레드로 색상 변경 후 부모 기준 회전 |
| Case 2 | 블랙 (Black) | 모두 블랙 (Black) | 형제를 레드로 변경 후 이중 블랙을 부모로 전파 |
| Case 3-1 | 블랙 (Black) | 반대 방향의 조카가 레드 | 조카를 블랙으로, 형제를 레드로 색상 변경 후 형제 기준 회전 및 Case 3-2 수행 |
| Case 3-2 | 블랙 (Black) | 같은 방향의 조카가 레드 | 형제, 부모, 조카의 색상 변경 후 부모 기준 회전 |
-
좌우 대칭 처리: 만약 삭제된 노드가 부모의 오른쪽 자식일 경우, 동일한 과정을 대칭적으로 적용하여 문제를 해결합니다. (left가 right가 되고, right가 left가 된 것입니다)
-
루트 도달: 문제를 해결한 후에는 노드를 루트로 설정하고, 최종적으로 해당 노드를 블랙으로 설정합니다. (Case 2처럼 위로 전파하는 경우엔 루트로 설정되는 과정은 실행되지 않습니다)
이 과정을 통해 삭제 후 발생할 수 있는 트리의 불균형을 색상 변경과 회전을 통해 해결하며, Red-Black Tree의 특성을 유지합니다.
6. Red-Black Tree 직접 구현해보기 - Python
이번 섹션에서는 Red-Black Tree를 Python으로 직접 구현하는 방법을 살펴보겠습니다.
Python에서는 TreeMap과 같은 내장된 Red-Black Tree 구조가 없기 때문에, 기본적인 노드 클래스와 트리 클래스를 구현해야 합니다.
Python으로 Red-Black Tree를 구현할 때 기본적으로 필요한 기능은 다음과 같습니다:
- 삽입 연산: 새로운 값을 트리에 삽입하고, 삽입 후 트리의 균형을 유지하는 과정.
- 삭제 연산: 값을 삭제한 후 트리의 균형을 유지하는 과정.
- 탐색 연산: 트리에서 특정 값을 탐색하는 과정.
6.1 Red-Black Tree 노드 클래스 구현
Red-Black Tree의 노드는 다음과 같은 정보를 포함합니다:
- 키와 값: 노드가 저장하는 데이터.
- 색상: 노드가 Red 또는 Black인지를 나타냅니다.
- 부모, 왼쪽 자식, 오른쪽 자식: 트리 구조에서 다른 노드와의 연결을 유지합니다.
class Node:
def __init__(self, key, value, color='RED', parent=None, left=None, right=None):
self.key = key # 노드의 키
self.value = value # 노드의 값
self.color = color # 노드의 색상 (기본적으로 RED로 삽입)
self.parent = parent # 부모 노드
self.left = left # 왼쪽 자식 노드
self.right = right # 오른쪽 자식 노드
def __repr__(self):
return f'Node({self.key}, {self.value}, {self.color})'
def is_red(self):
return self.color == 'RED'
def is_black(self):
return self.color == 'BLACK'6.2 Red-Black Tree 트리 클래스 구현
이제 트리 클래스를 정의해보겠습니다. 트리 클래스는 노드를 관리하고, 삽입 및 삭제 연산을 수행한 후 균형을 유지하는 역할을 합니다.
6.2.1 트리 초기화
트리를 초기화할 때 루트 노드를 정의하고, 필요한 유틸리티 메서드를 추가합니다.
- 탐색(
search) 메서드 - 회전 연산 메서드(
left_rotate,right_rotate)
class RedBlackTree:
def __init__(self):
self.NIL = Node(None, None, color='BLACK') # 모든 NIL 노드는 BLACK으로 처리
self.root = self.NIL # 초기에는 루트가 NIL
# 주어진 키에 대해 트리에서 해당 노드를 검색
def search(self, key):
return self._search(self.root, key)
def _search(self, node, key):
# 현재 노드가 NIL이거나 키가 일치하면 해당 노드를 반환
if node == self.NIL or key == node.key:
return node
# 키가 현재 노드의 키보다 작으면 왼쪽 서브트리를 탐색
if key < node.key:
return self._search(node.left, key)
# 키가 현재 노드의 키보다 크면 오른쪽 서브트리를 탐색
else:
return self._search(node.right, key)
# 좌회전을 수행하여 x를 기준으로 트리의 구조를 변경
def left_rotate(self, x):
y = x.right # x의 오른쪽 자식 y
x.right = y.left # y의 왼쪽 자식을 x의 오른쪽 자식으로
# y의 왼쪽 자식이 NIL이 아니면, 그 부모를 x로 설정
if y.left != self.NIL:
y.left.parent = x
y.parent = x.parent # y의 부모를 x의 부모로 설정
# 만약 x가 루트였다면 y를 새로운 루트로 설정
if x.parent is None:
self.root = y
# x가 부모의 왼쪽 자식인 경우
elif x == x.parent.left:
x.parent.left = y
# x가 부모의 오른쪽 자식인 경우
else:
x.parent.right = y
# y의 왼쪽 자식을 x로 설정하여 좌회전 완료
y.left = x
x.parent = y
# 우회전을 수행하여 x를 기준으로 트리의 구조를 변경
def right_rotate(self, x):
y = x.left
x.left = y.right
if y.right != self.NIL:
y.right.parent = x
y.parent = x.parent
if x.parent is None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
self.NIL: 모든NIL노드는 BLACK이므로 기본적으로NIL노드를 BLACK으로 설정합니다.self.root: 초기 루트 노드는NIL입니다.search: 주어진 키를 트리에서 탐색하는 메서드입니다. 이진 탐색 트리의 방식으로 재귀적으로 탐색합니다.left_rotate및right_rotate: 좌회전과 우회전을 수행하는 메서드입니다. 트리의 불균형을 해결하기 위해 사용됩니다.
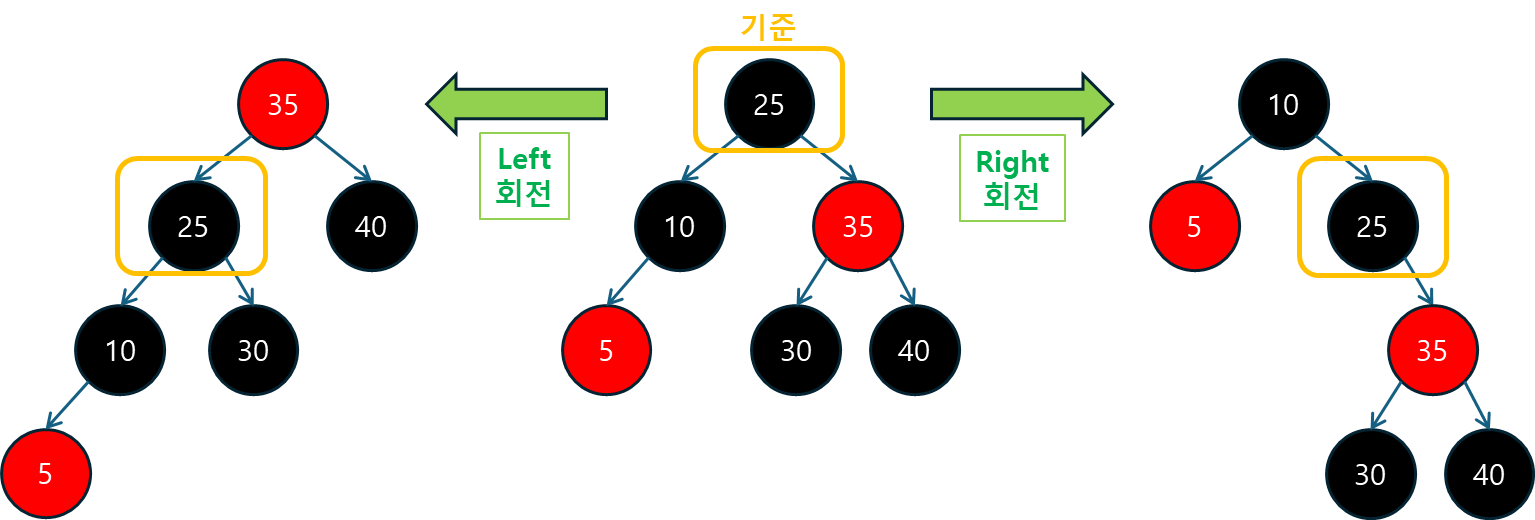
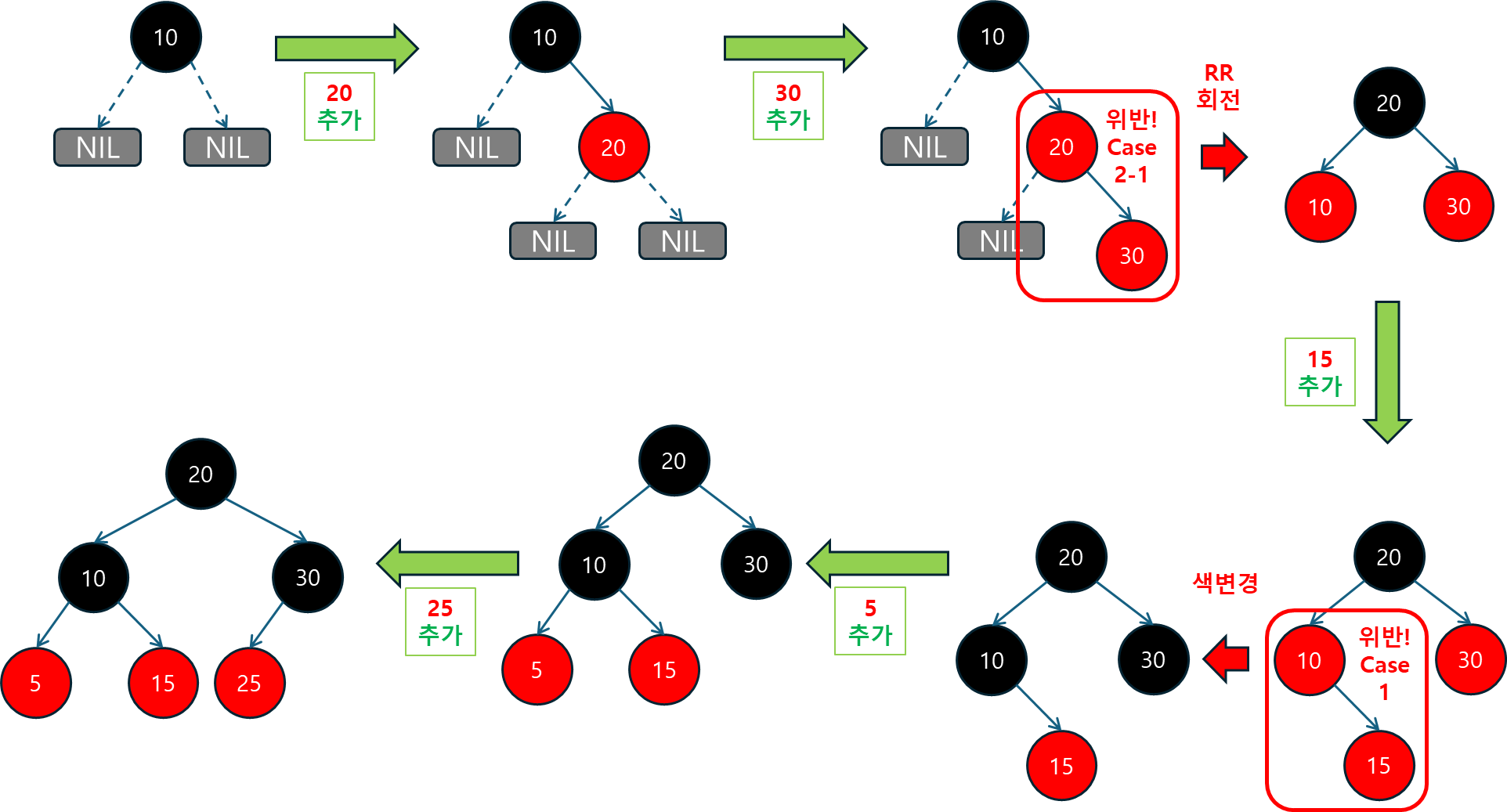
6.2.2 삽입 연산
삽입 연산은 새로운 값을 트리에 삽입하고, 삽입 후 트리의 균형을 유지하는 과정이 포함됩니다.
def insert(self, key, value):
node = Node(key, value, color='RED') # 새 노드는 기본적으로 RED로 삽입
parent = None
temp = self.root
# 트리 탐색을 통해 삽입할 위치를 찾음
while temp != self.NIL:
parent = temp
if node.key < temp.key:
temp = temp.left
else:
temp = temp.right
node.parent = parent
# 부모 노드와의 연결 설정
if parent is None:
self.root = node
node.color = 'BLACK' # 루트는 항상 BLACK
elif node.key < parent.key:
parent.left = node
else:
parent.right = node
# 새로 삽입된 노드의 자식은 NIL로 설정
node.left = self.NIL
node.right = self.NIL
# 루트가 아닌 경우에만 fix_insert 호출
if node != self.root:
self.fix_insert(node)
def fix_insert(self, k):
while k != self.root and k.parent.color == 'RED':
if k.parent == k.parent.parent.left: # 부모가 왼쪽 자식인 경우
u = k.parent.parent.right # 삼촌 노드
if u.color == 'RED': # Case 1: 삼촌이 RED인 경우
k.parent.color = 'BLACK'
u.color = 'BLACK'
k.parent.parent.color = 'RED'
k = k.parent.parent
else:
if k == k.parent.right: # Case 2-2: 부모가 왼쪽인데, 자식이 오른쪽인 경우
k = k.parent
self.left_rotate(k)
k.parent.color = 'BLACK' # Case 2-1: 부모가 RED, 삼촌이 BLACK인 경우
k.parent.parent.color = 'RED'
self.right_rotate(k.parent.parent)
else: # 부모가 오른쪽 자식인 경우
u = k.parent.parent.left # 삼촌 노드
if u.color == 'RED':
k.parent.color = 'BLACK'
u.color = 'BLACK'
k.parent.parent.color = 'RED'
k = k.parent.parent
else:
if k == k.parent.left:
k = k.parent
self.right_rotate(k)
k.parent.color = 'BLACK'
k.parent.parent.color = 'RED'
self.left_rotate(k.parent.parent)
self.root.color = 'BLACK' # 루트는 항상 BLACK
- 삽입할 위치 찾기: 새로운 노드를 삽입할 적절한 위치를 찾습니다. 이는 이진 탐색 트리와 동일한 방식으로 이루어집니다.
- 새 노드 연결: 부모 노드와 연결된 자식 노드로 새 노드를 삽입합니다.
- 트리 균형 유지:
fix_insert메서드를 호출하여, 삽입 후 트리의 규칙이 깨진 경우 이를 회전과 색상 변경을 통해 해결합니다.- Case 1: 삼촌 노드가 RED인 경우 부모와 삼촌을 BLACK으로, 조부모를 RED로 변경하고 전파합니다.
- Case 2-2: 삼촌이 BLACK이고, 부모가 왼쪽 자식인데 삽입된 노드가 오른쪽 자식인 경우 회전합니다. (반대 방향도 마찬가지입니다.)
- Case 2-1: 삼촌이 BLACK이고 삽입된 노드가 왼쪽 자식일 때, 부모와 조부모의 색상 변경 후 회전합니다.
| 경우 | 부모 노드 색상 | 형제(삼촌) 노드 색상 | 해결 방법 |
|---|---|---|---|
| Case 1 | 레드 (Red) | 레드 (Red) | 색상 변경: 부모와 형제를 블랙으로, 조부모를 레드로 변경. 조부모가 루트가 아닐 경우 상위 노드로 색상 위반 문제 전파 |
| Case 2-1 (단일 회전) | 레드 (Red) | 블랙 (Black) 혹은 NIL | 단일 회전: 부모와 삽입된 노드가 조부모와 같은 방향에 있을 경우 단일 회전(LL 또는 RR)으로 재구조화 실시 |
| Case 2-2 (이중 회전) | 레드 (Red) | 블랙 (Black) 혹은 NIL | 이중 회전: 부모와 삽입된 노드가 조부모와 반대 방향에 있을 경우 이중 회전(LR 또는 RL)으로 재구조화 실시 |
6.2.3 후계자 노드와 트리 대체를 위한 메서드 정의
삭제 연산 구현 전에 transplant와 minimum메서드를 정의합니다.
- 이 두 메서드는 Red-Black Tree의 삭제 과정에서 중요한 역할을 하며, 삭제할 노드를 대체할 후계자 노드를 찾거나, 노드 대체 작업을 수행하는 데 사용됩니다.
transplant 메서드
transplant 메서드는 트리에서 두 노드를 교체하는 작업을 수행합니다.
- 즉, 하위 트리를 다른 하위 트리로 교체하는 기능을 합니다.
- 이는 노드를 삭제하거나 후계자 노드를 찾을 때 중요한 역할을 합니다.
def transplant(self, u, v):
""" u 노드를 v 노드로 교체 """
if u.parent is None: # u가 루트인 경우
self.root = v # v를 새로운 루트로 설정
elif u == u.parent.left:
u.parent.left = v # u가 왼쪽 자식인 경우
else:
u.parent.right = v # u가 오른쪽 자식인 경우
v.parent = u.parent # v의 부모를 u의 부모로 설정
transplant(u, v)는 트리에서 노드 u를 v로 대체합니다.- 만약 u가 루트라면 v가 새로운 루트가 됩니다.
- u가 부모의 왼쪽 자식이라면, 부모의 왼쪽 자식에 v를 설정합니다. 오른쪽 자식이라면, 부모의 오른쪽 자식에 v를 설정합니다.
- 마지막으로, v의 부모를 u의 부모로 설정하여 트리의 연결을 갱신합니다.
minimum 메서드
minimum 메서드는 서브트리에서 가장 작은 값을 가진 노드(후계자)를 찾습니다.
- Red-Black Tree의 삭제 시, 삭제할 노드가 두 자식을 가진 경우 후계자 노드를 찾는 과정에서 사용됩니다.
def minimum(self, node):
""" 주어진 서브트리에서 가장 작은 키를 가진 노드를 반환 """
while node.left != self.NIL: # 왼쪽 자식이 NIL이 아닐 때까지 반복
node = node.left # 왼쪽으로 계속 이동
return node
minimum(node)는 주어진 서브트리(주로 오른쪽 서브트리)에서 가장 작은 값을 가진 노드를 반환합니다.- 이진 탐색 트리에서 가장 작은 값은 왼쪽 서브트리의 끝에 위치하므로, 왼쪽 자식이 NIL이 될 때까지 왼쪽으로 이동합니다.
- 찾은 가장 작은 노드를 반환합니다.
6.2.4 삭제 연산
삭제 연산은 삭제한 후 트리의 균형을 복구하는 과정이 포함됩니다.
def delete(self, key):
# 삭제할 노드를 탐색
node = self.search(key)
if node == self.NIL:
return # 삭제할 노드를 찾지 못하면 종료
y = node
y_original_color = y.color # 삭제할 노드의 원래 색상 저장
# 왼쪽 자식이 없는 경우 (오른쪽 서브트리와 교환)
if node.left == self.NIL:
x = node.right
self.transplant(node, node.right)
# 오른쪽 자식이 없는 경우 (왼쪽 서브트리와 교환)
elif node.right == self.NIL:
x = node.left
self.transplant(node, node.left)
# 두 자식이 있는 경우, 후계자 노드를 찾음
else:
# 오른쪽 서브트리에서 가장 작은 노드(후계자) 찾기
y = self.minimum(node.right)
y_original_color = y.color # 후계자의 원래 색상 저장
x = y.right
if y.parent == node:
x.parent = y
else:
# 후계자 노드를 삭제할 노드 자리로 옮김
self.transplant(y, y.right)
y.right = node.right
y.right.parent = y
# 삭제할 노드를 후계자로 대체
self.transplant(node, y)
y.left = node.left
y.left.parent = y
y.color = node.color # 후계자의 색상을 삭제할 노드의 색상으로 설정
# 삭제된 노드가 블랙일 경우, 트리의 균형을 맞춤
if y_original_color == 'BLACK':
self.fix_delete(x)
# 삭제 후 균형을 맞추는 과정 (x는 이중 블랙 상태)
def fix_delete(self, x):
while x != self.root and x.color == 'BLACK':
# x가 부모의 왼쪽 자식인 경우
if x == x.parent.left:
w = x.parent.right # 형제 노드
# Case 1: 형제가 RED인 경우
if w.color == 'RED':
w.color = 'BLACK' # 형제를 블랙으로 변경
x.parent.color = 'RED' # 부모를 레드로 변경
self.left_rotate(x.parent) # 부모 기준으로 좌회전
w = x.parent.right # 회전 후 새로운 형제 노드 갱신
# Case 2: 형제와 그 자식(조카)들이 모두 BLACK인 경우
if w.left.color == 'BLACK' and w.right.color == 'BLACK':
w.color = 'RED' # 형제를 레드로 변경
x = x.parent # 이중 블랙을 부모로 전파
else:
# Case 3-1: 형제의 왼쪽 자식(조카)이 RED인 경우
if w.right.color == 'BLACK':
w.left.color = 'BLACK' # 조카를 블랙으로 변경
w.color = 'RED' # 형제를 레드로 변경
self.right_rotate(w) # 형제 기준으로 우회전
w = x.parent.right # 새로운 형제 노드 설정
# Case 3-2: 형제의 오른쪽 자식이 RED인 경우
w.color = x.parent.color # 형제의 색상을 부모의 색상으로 설정
x.parent.color = 'BLACK' # 부모를 블랙으로 변경
w.right.color = 'BLACK' # 형제의 오른쪽 자식을 블랙으로 변경
self.left_rotate(x.parent) # 부모 기준으로 좌회전
x = self.root # 루트로 설정하고 반복문 종료
# 부모의 오른쪽 자식인 경우 (대칭 처리)
else: # symmetric
w = x.parent.left
if w.color == 'RED':
w.color = 'BLACK'
x.parent.color = 'RED'
self.right_rotate(x.parent)
w = x.parent.left
if w.right.color == 'BLACK' and w.left.color == 'BLACK':
w.color = 'RED'
x = x.parent
else:
if w.left.color == 'BLACK':
w.right.color = 'BLACK'
w.color = 'RED'
self.left_rotate(w)
w = x.parent.left
w.color = x.parent.color
x.parent.color = 'BLACK'
w.left.color = 'BLACK'
self.right_rotate(x.parent)
x = self.root
# 마지막으로 x의 색상을 BLACK으로 설정하여 이중 블랙 상태를 해소
x.color = 'BLACK'
delete 메서드:
- 후계자 선택: 삭제할 노드가 두 자식을 가지고 있는 경우, 오른쪽 서브트리에서 가장 작은 노드를 찾아 후계자로 사용합니다.
- 후계자 대체: 후계자를 삭제할 노드의 위치에 옮기고, 후계자의 색상을 삭제할 노드의 색상으로 설정하여 트리 구조를 유지합니다.
fix_delete 메서드:
- Case 1: 형제가 RED인 경우, 형제를 BLACK으로, 부모를 RED로 바꾼 후, 부모를 기준으로 회전을 수행해 균형을 맞춥니다.
- Case 2: 형제와 그 자식(조카)들이 모두 BLACK인 경우, 형제를 RED로 바꾸고 이중 블랙을 부모로 전파합니다.
- Case 3-1, 3-2: 형제의 자식(조카) 중 RED인 자식이 있을 때, 조카의 색상에 따라 회전 및 색상 변경을 수행하여 트리의 균형을 유지합니다.
| 경우 | 형제 노드 색상 | 조카 노드 상태 | 해결 방법 |
|---|---|---|---|
| Case 1 | 레드 (Red) | 상관없음 | 형제를 블랙으로, 부모를 레드로 색상 변경 후 부모 기준 회전 |
| Case 2 | 블랙 (Black) | 모두 블랙 (Black) | 형제를 레드로 변경 후 이중 블랙을 부모로 전파 |
| Case 3-1 | 블랙 (Black) | 반대 방향의 조카가 레드 | 조카를 블랙으로, 형제를 레드로 색상 변경 후 형제 기준 회전 및 Case 3-2 수행 |
| Case 3-2 | 블랙 (Black) | 같은 방향의 조카가 레드 | 형제, 부모, 조카의 색상 변경 후 부모 기준 회전 |
6.3 테스트 케이스 추가
Red-Black Tree가 올바르게 동작하는지 확인하기 위해 삽입, 탐색, 삭제를 포함한 테스트 케이스를 작성해볼 수 있습니다.
- 트리의 균형이 제대로 유지되고, 각 연산이 정상적으로 수행되는지 확인하기 위해 다양한 키와 값을 삽입, 삭제하며 테스트할 수 있습니다.
다음은 테스트 케이스를 작성하고 실행하는 예시입니다.
def test_red_black_tree():
print("=== Red-Black Tree 테스트 시작 ===")
# 새로운 Red-Black Tree 생성
rbt = RedBlackTree()
# 삽입 테스트 (10 -> 20 -> 30 -> 15 -> 5 -> 25 순서)
rbt.insert(10, "Value10")
rbt.insert(20, "Value20")
rbt.insert(30, "Value30")
rbt.insert(15, "Value15")
rbt.insert(5, "Value5")
rbt.insert(25, "Value25")
print("\n--- 삽입 후 트리 구조 ---")
print_tree(rbt.root, "", True)
# 탐색 테스트 (15)
print("\n--- 탐색 테스트 ---")
node = rbt.search(15)
if node != rbt.NIL:
print(f"키 15에 대한 값: {node.value}")
else:
print("키 15를 찾지 못했습니다.")
# 탐색 테스트 (50)
node = rbt.search(50)
if node != rbt.NIL:
print(f"키 50에 대한 값: {node.value}")
else:
print("키 50를 찾지 못했습니다.")
# 삭제 테스트 (20 -> 5 -> 30 순서로 삭제 및 트리 확인)
print("\n--- 삭제 테스트: 키 20 삭제 ---")
rbt.delete(20)
print_tree(rbt.root, "", True)
print("\n--- 삭제 테스트: 키 5 삭제 ---")
rbt.delete(5)
print_tree(rbt.root, "", True)
print("\n--- 삭제 테스트: 키 30 삭제 ---")
rbt.delete(30)
print_tree(rbt.root, "", True)
print("=== 테스트 완료 ===")
def print_tree(node, indent, last):
""" 트리 구조를 시각적으로 출력하기 위한 헬퍼 함수 """
if node is not None and node.key is not None:
print(indent, "`- " if last else "|- ", f"({node.key}, {node.value}, {node.color})", sep="")
indent += " " if last else "| "
print_tree(node.left, indent, False)
print_tree(node.right, indent, True)
# 테스트 실행
test_red_black_tree()
-
삽입 테스트:
- 키와 값을 가진 노드를 트리에 삽입하고, 삽입 후 트리 구조가 올바르게 형성되는지 확인합니다.
- 여러 값을 삽입해 트리의 균형을 유지하며, 각 노드가 올바른 위치와 색상을 가지는지 테스트합니다.
-
탐색 테스트:
- 트리에 삽입된 값을 탐색하고, 올바른 값을 찾는지를 테스트합니다.
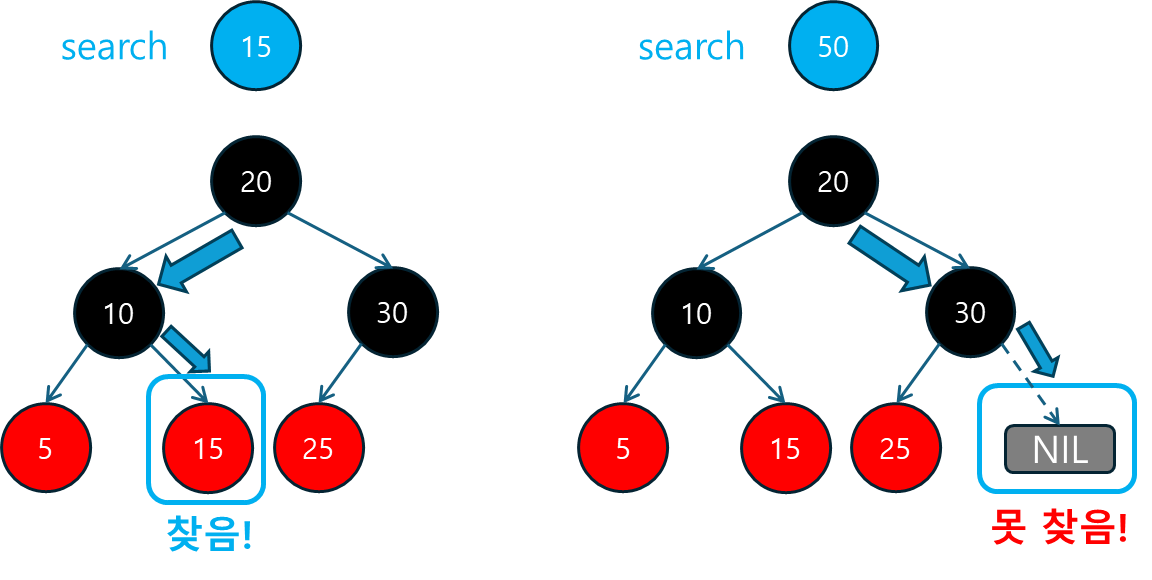
- 존재하지 않는 키를 탐색할 때,
NIL노드가 반환되는지 확인합니다.
-
삭제 테스트:
- 삽입된 키를 삭제하고, 트리의 균형을 유지하며 삭제가 정상적으로 이루어졌는지 확인합니다.
- 여러 단계에 걸쳐 키를 삭제하며, 회전 및 색상 변경이 올바르게 이루어지는지 확인합니다.
테스트 결과
=== Red-Black Tree 테스트 시작 ===
--- 삽입 후 트리 구조 ---
`- (20, Value20, BLACK)
|- (10, Value10, BLACK)
| |- (5, Value5, RED)
| `- (15, Value15, RED)
`- (30, Value30, BLACK)
|- (25, Value25, RED)
--- 탐색 테스트 ---
키 15에 대한 값: Value15
키 50를 찾지 못했습니다.
--- 삭제 테스트: 키 20 삭제 ---
`- (25, Value25, BLACK)
|- (10, Value10, BLACK)
| |- (5, Value5, RED)
| `- (15, Value15, RED)
`- (30, Value30, BLACK)
--- 삭제 테스트: 키 5 삭제 ---
`- (25, Value25, BLACK)
|- (10, Value10, BLACK)
| `- (15, Value15, RED)
`- (30, Value30, BLACK)
--- 삭제 테스트: 키 30 삭제 ---
`- (15, Value15, BLACK)
|- (10, Value10, BLACK)
`- (25, Value25, BLACK)
=== 테스트 완료 ===
테스트 결과 분석
- 삽입 후 트리 구조는 Red-Black Tree의 규칙에 따라 색상 및 균형이 잘 유지되었습니다.
--- 삽입 후 트리 구조 ---
`- (20, Value20, BLACK)
|- (10, Value10, BLACK)
| |- (5, Value5, RED)
| `- (15, Value15, RED)
`- (30, Value30, BLACK)
|- (25, Value25, RED)- 탐색 테스트에서는 삽입된 키
15에 대해 정상적으로 값을 찾았으며, 존재하지 않는 키50에 대해서는 찾지 못했다는 결과를 출력했습니다.
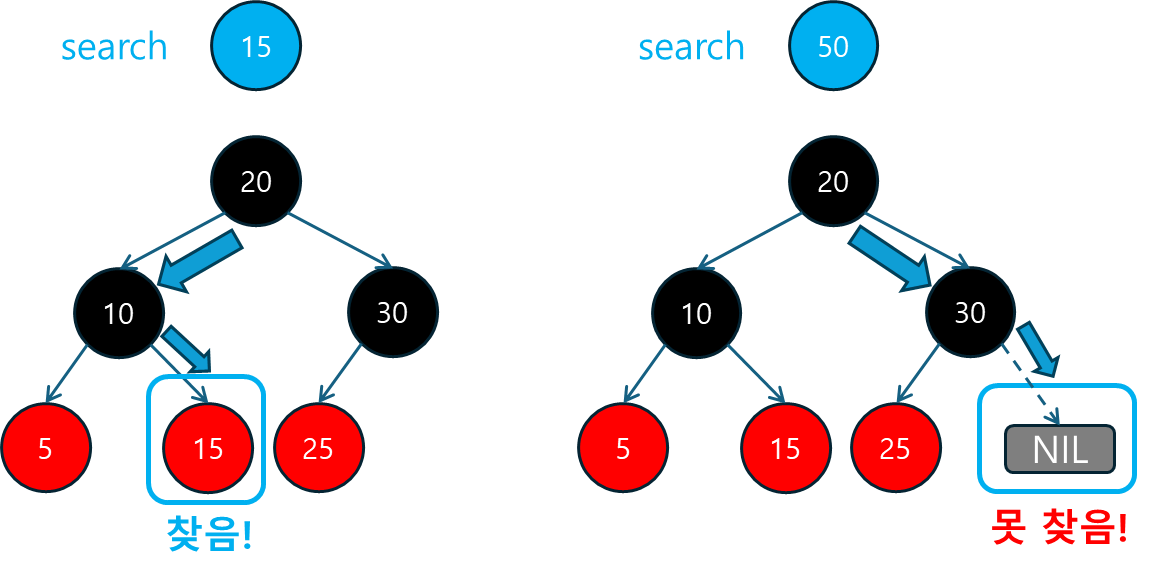
--- 탐색 테스트 ---
키 15에 대한 값: Value15
키 50를 찾지 못했습니다.- 삭제 후에도 트리의 균형이 잘 유지되었고, 이중 블랙 문제도 회전 및 색상 변경을 통해 해결되었습니다.
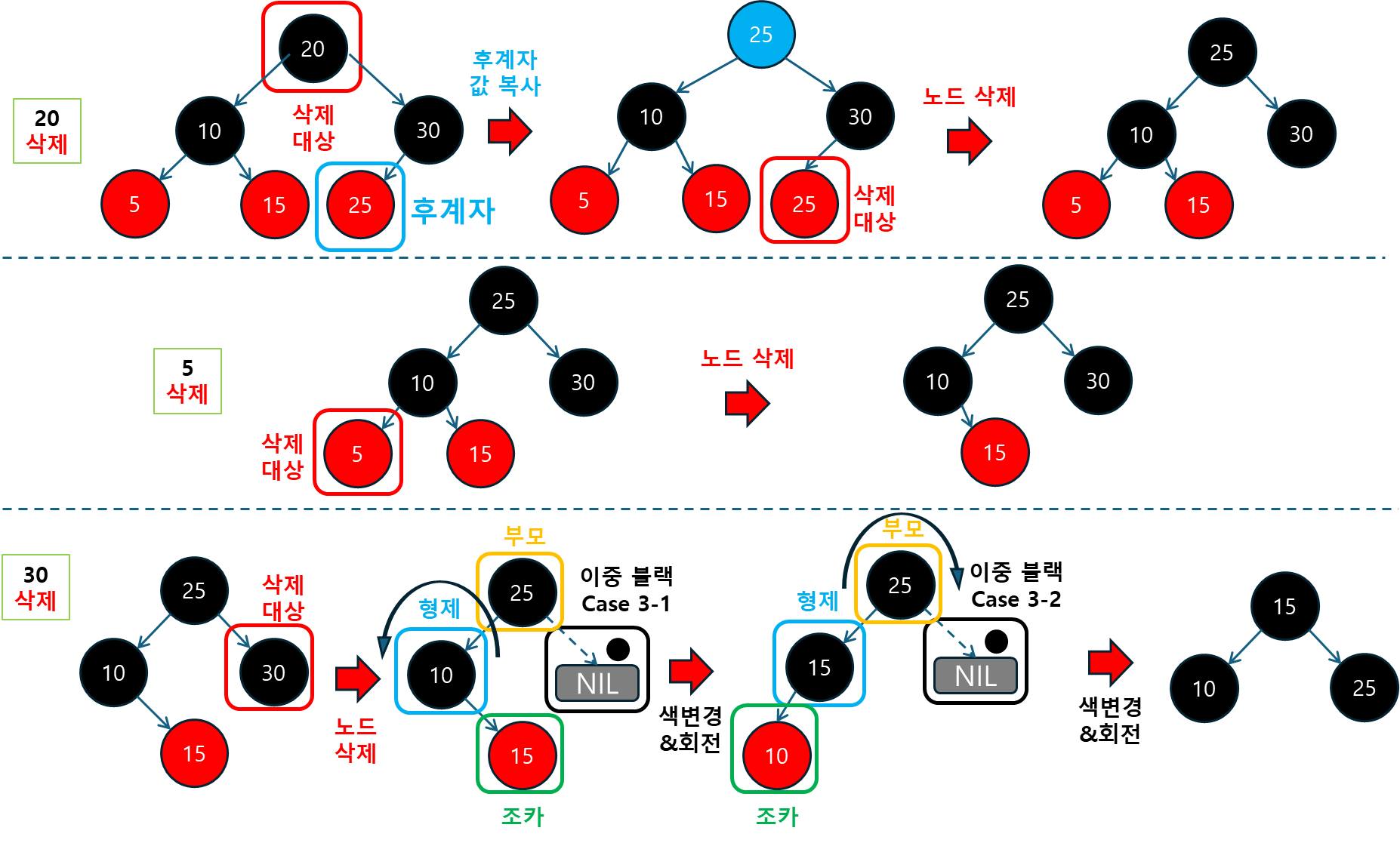
--- 삭제 테스트: 키 20 삭제 ---
`- (25, Value25, BLACK)
|- (10, Value10, BLACK)
| |- (5, Value5, RED)
| `- (15, Value15, RED)
`- (30, Value30, BLACK)
--- 삭제 테스트: 키 5 삭제 ---
`- (25, Value25, BLACK)
|- (10, Value10, BLACK)
| `- (15, Value15, RED)
`- (30, Value30, BLACK)
--- 삭제 테스트: 키 30 삭제 ---
`- (15, Value15, BLACK)
|- (10, Value10, BLACK)
`- (25, Value25, BLACK)이러한 테스트 케이스를 통해 삽입, 삭제, 탐색 연산이 올바르게 동작하고, Red-Black Tree의 특성(균형 및 색상 규칙)이 잘 유지되는지 확인할 수 있었습니다.
마무리
이번 포스팅에서는 Java의 TreeMap을 활용한 Red-Black Tree의 내부 동작 원리를 분석하고, 이어서 Python에서 Red-Black Tree를 직접 구현하는 과정을 살펴보았습니다.
TreeMap은 내부적으로 Red-Black Tree를 사용하여 데이터를 저장하며, 정렬된 상태에서 삽입, 삭제, 탐색 연산을 O(log n)의 시간 복잡도로 처리할 수 있는 효율적인 자료구조입니다.
- 이는 실시간으로 데이터를 처리하고, 정렬된 결과를 빠르게 제공해야 하는
Map또는Set기반 시스템에서 매우 중요한 역할을 합니다.
또한, Python에서는 기본적으로 내장된 Red-Black Tree가 없기 때문에, 직접 구현을 통해 회전 연산과 색상 변경을 사용한 트리 균형 유지 방식을 살펴보았습니다.
저번 포스팅을 포함해서 Red-Black Tree의 이론적 원리와 실무적인 적용 방식을 잘 이해하고, 이를 기반으로 다양한 응용 시스템에 적용할 수 있기를 바랍니다.
