1. Sympathetic Magic
- mistake of confusing r.v. with its distribution.
- adding r.v.s are not the same as adding pmfs.
- can be bigger than 1.
- you can’t do things like this.
- “Word is not the thing, the map is not the territory.”
- r.v. = random house, dist. = blueprint
- you can have many r.v.s with the same dist.
- blueprint : specifying all the probabilities for randomly choosing the color of doors of the house.
2. Poisson Distribution
- Most important discrete distribution.
- PMF
- is the rate parameter. () → param of poisson dist.
- Valid?
- ( adding PMF = 1)
- by taylor series. check!!
- expected value
- (when k=0, it’s 0 anyway)
- (when k=0, it’s 0 anyway)
- ( adding PMF = 1)
Why do we care about Poisson?
- It’s the most used dist. as a model for discrete data in the real world.
1) General Applications
- Counting number of successes where there are a large number of trials each with small prob. of success.
- Examples ( Not exactly, but approximately Poisson)
- number of emails in an hour
- Number of chocolate chips in a chocolate chip cookie
- Number of earthquakes in a year in some region
- There is no upper bound in as it goes towards infinity, and the prob. being small is not that clear (how small?)
- so it is useful to approximate a real world dist. with a poisson dist.
2) Poisson Paradigm (Poisson Approximation)
-
Event , , n large, ’s small.
- large number of trials, each unlikely
-
Events are independent or weakly dependent, then number of ’s that occur is approximately Poisson. →
- weakly dependent is hard to define.
- we could get a little bit of information.
- if we know happened, maybe it helps a little bit to know if happened.
- we could get a little bit of information.
- weakly dependent is hard to define.
-
Expected Number of events occuring =
- If all events are independent & ’s are all the same, we have Bernoulli trials
- Expected Value =
- If all events are independent & ’s are all the same, we have Bernoulli trials
3) Connection between &
- Let (n is large number), is held constant.
- Each are expected values for Binomial & Poisson
- Find what happens to the PMF , k fixed.
- , so plug it in.
- ( 조합의 정의)
→ 이제 limit을 취하자. ()
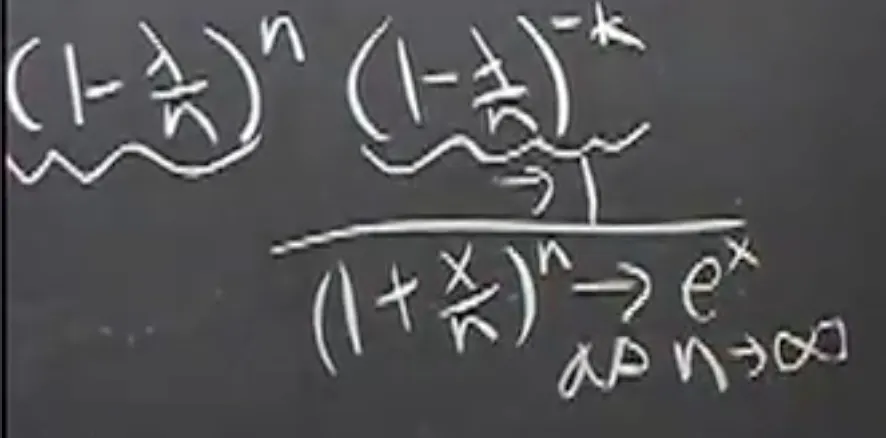
- 은 로 감.
- (limit 취하고 남은 값.)
→ Poisson PMF at k.
- So, Binomial converges to Poisson when .
Raindrop Example
- We have a piece of paper, and we want to know how many raindrops hit this paper in 1 minute.
- let’s break the paper into millions of tiny squares. ( )
- each square is unlikely to be hit by a raindrop.
- If we assume all squares are independent, probability is all the same, binomial is what we should use.
- Probably not exactly independent.
- Also, binomial only takes Y/N.
- what if a square gets hit 2 times? → no way to express this by binomial
- Poisson Dist. seems better.
Triple birthday problem
- Have n people, find the approx. prob. that there are 3 people that have the same birthday.
- Assume n is reasonably large number.
- triplets of people, indicator r.v. for each,
- if they all have the same birthday.
- 1st person can have whatever birthday, and the 2nd person should match the 1st person (1/365), and the 3rd person should match the 2nd person.(1/365)
- Let → this is approximately ,
- each triplets matching birthdays is unlikely, n is fairly large.
- We don’t exactly have independence.
- are not completely independent. (weak dependence)
- if we already know that 1,2 have the same birthday when we compute
- (prob. of at least one triple match)
→ poisson is very useful for getting rough approximations.
