Statistics 110

    3/20부터 사회복무요원 근무를 하고 있는데, 적응하는데 시간이 예상보다 많이 걸렸다. 육체적으로 힘들다 보니 논문을 읽는 것보다 강의를 보는 것이 다시 공부하는 습관을 잡는데 좋을 것 같다는 생각이 들었다. 그래서 평소에도 부족한 부분이라고 생각했던 확률과 통

&nbsp &nbsp 이전 글에 이어서 두 번째, 세 번째 강의이다. 먼저 Lecture 2부터 살펴보자. 1. Lecture 2 &nbsp &nbsp 이번 강의에서는 story proof, 즉 수식적인 증명이 아닌 해석을 통해 증명을 하는 방법을 다룬다. 확률과 통계

1. Lecture 4 &nbsp &nbsp Lecture 4는 독립(Independence), 조건부 확률(Conditional Probability)에 대한 내용이다. 개인적으로 조건부 확률의 개념을 설명하는 방식이 굉장히 인상 깊었다. 1) Independenc

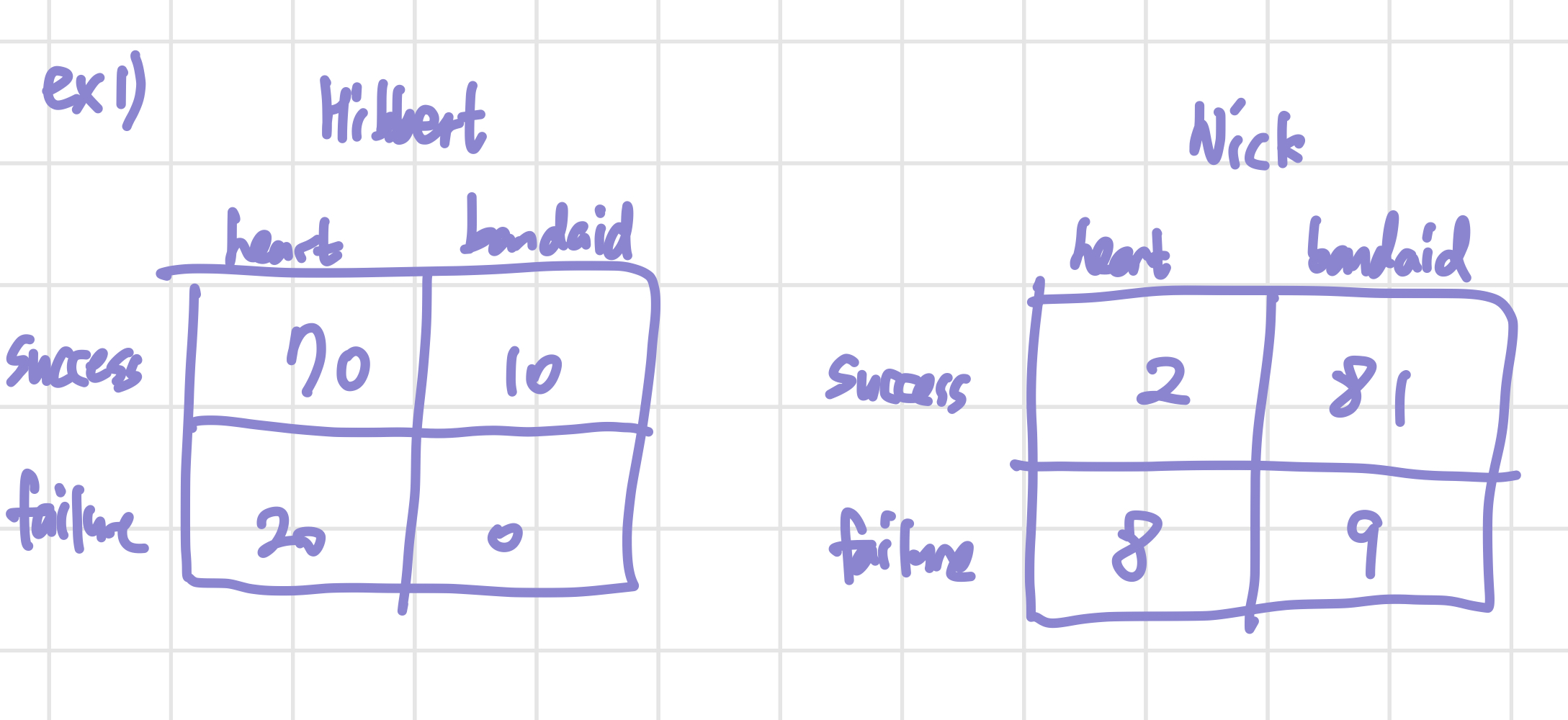
1. Lecture 6 &nbsp &nbsp Lecture 6에서는 Monty Hall problem, Simpson's Paradox에 대해서 이야기 한다. 먼저 Monty Hall 문제부터 살펴보자. 1) Monty Hall Problem &nbsp &nbsp 이

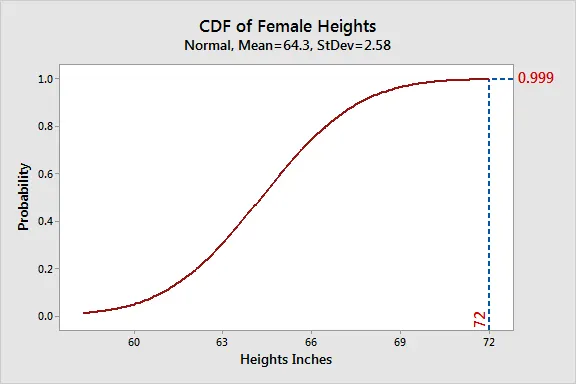
1. Lecture 8 &nbsp &nbsp Lecture 8에서는 이전 강의에서 이야기하던 Random variable과 그 분포에 대한 내용을 계속해서 다룬다. 먼저 Binomial Distribution에 대해서 이어서 알아보자. 1) Binomial Distr

Let $T = X + Y$, show $E(T) = E(X) + E(Y)$ (assume r.v.s are discrete)this is true even if X,Y are dependent.pf1) $\\sum{t} t \\ P(T=t) = \\sum{x} x \

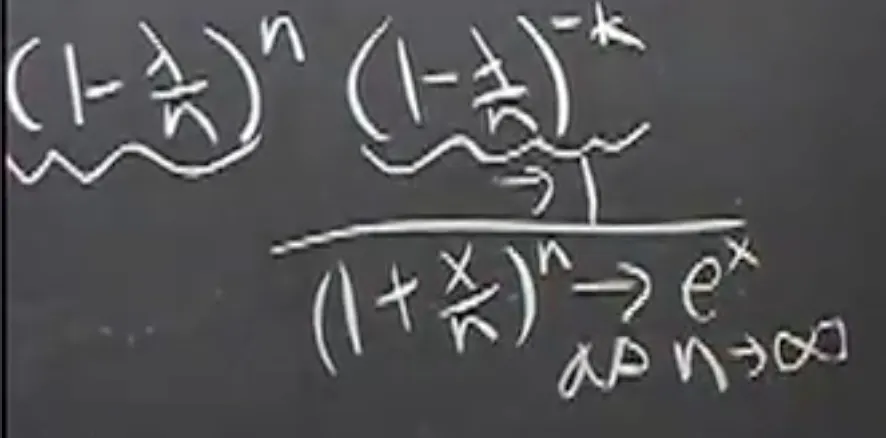
mistake of confusing r.v. with its distribution.adding r.v.s are not the same as adding pmfs.$P(X=x) + P(Y=y)$can be bigger than 1.you can’t do things