[Cryptanalysis] Hill Cipher

해당 글은 다음 논문을 참고하였습니다.
Shahram Khazaei, Siavash Ahmadi, Ciphertext-only attack on d×d Hill in O(d13d)

1. 서론
   Hill cipher, 행렬을 활용하여 암호화하는 고전 암호다.
   $key = \begin{bmatrix} k_{11} & k_{12} \;...\;k_{1d} \\ k_{21} & k_{22} \;...\;k_{2d} \\ \dots \\ k_{d1} & k_{d2} \;...\;k_{dd} \end{bmatrix}$

key가 위와 같이 dxd 크기 행렬일 때 plaintext와 ciphertext는 d크기의 vector로 나누어져 블록암호처럼 암호화된다.

복호화는 key의 역행렬을 곱해주면 된다.

이번 toy cipher에서는 암호문이 주어진 경우 키 복구를 통해 평문을 구해보았다.

2. d 결정
   cipher의 길이가 955로 5x191이라는 것을 알 수 있다. 블록으로 처리해야 하기 때문에 d = 5나 d = 191인데, d = 5가 더 현실성 있어 보이기 때문에 5로 선택한다.

3. IML (index of most likelihood)

IC와 비슷한 방식으로 해당 문장의 적합성을 판단한다.

실제 알파벳 빈도와 복호화된 평문 사이의 관계를 바로 보여주며(COA에서 판단하기 좋음) 훨씬 더 계산이 빠르기 때문에 26^5 계산을 통해 알맞은 키를 찾아야 하는 상황에서는 IML이 IC보다 유리하다.

4. 행렬이 아닌 열 단위로 계산

원래라면 5x5 크기의 행렬을 한 번에 구하려면 26^25번의 계산을 해야 하기 때문에 brute-forcing이 불가하다. 하지만 우리가 생각해야 할 점은 각 블록과 키의 열을 곱해서 하나의 문자를 생성한다는 점이다. 즉, 전체 행렬이 아닌 열을 단위로 하여 키를 구해도 문제가 없다는 것이다.

예를 들어 암호문을 키와 연산하면 키에 따라 총 5개의 평문 집합(크기는 191)이 나온다. 그런데 각 키는 모든 암호문과 곱해져서 결과가 나오기 때문에 각 평문 집합에서 IML을 계산해도 전체의 빈도를 고려하기 때문에 상관없다. 즉, 키를 5x5 행렬 세트로 보는게 아니라 제일 적합한 키벡터(5x1) 5개만 구해도 된다.

5. 시간 복잡도 감소

우리가 키를 brute-forcing 하기 위해서는 반복문을 쓸 수밖에 없다. 반복문의 특징은 +1씩 하나씩 증가한다는 것이다.

[25, 24, 23, 22, 21] -> [0, 25, 23, 22, 21] -> [1, 25, 23, 22, 21]

수의 받아올림처럼 작동한다. 이걸 활용하면 모든 plaintext를 일일이 계산하지 않아도 된다.

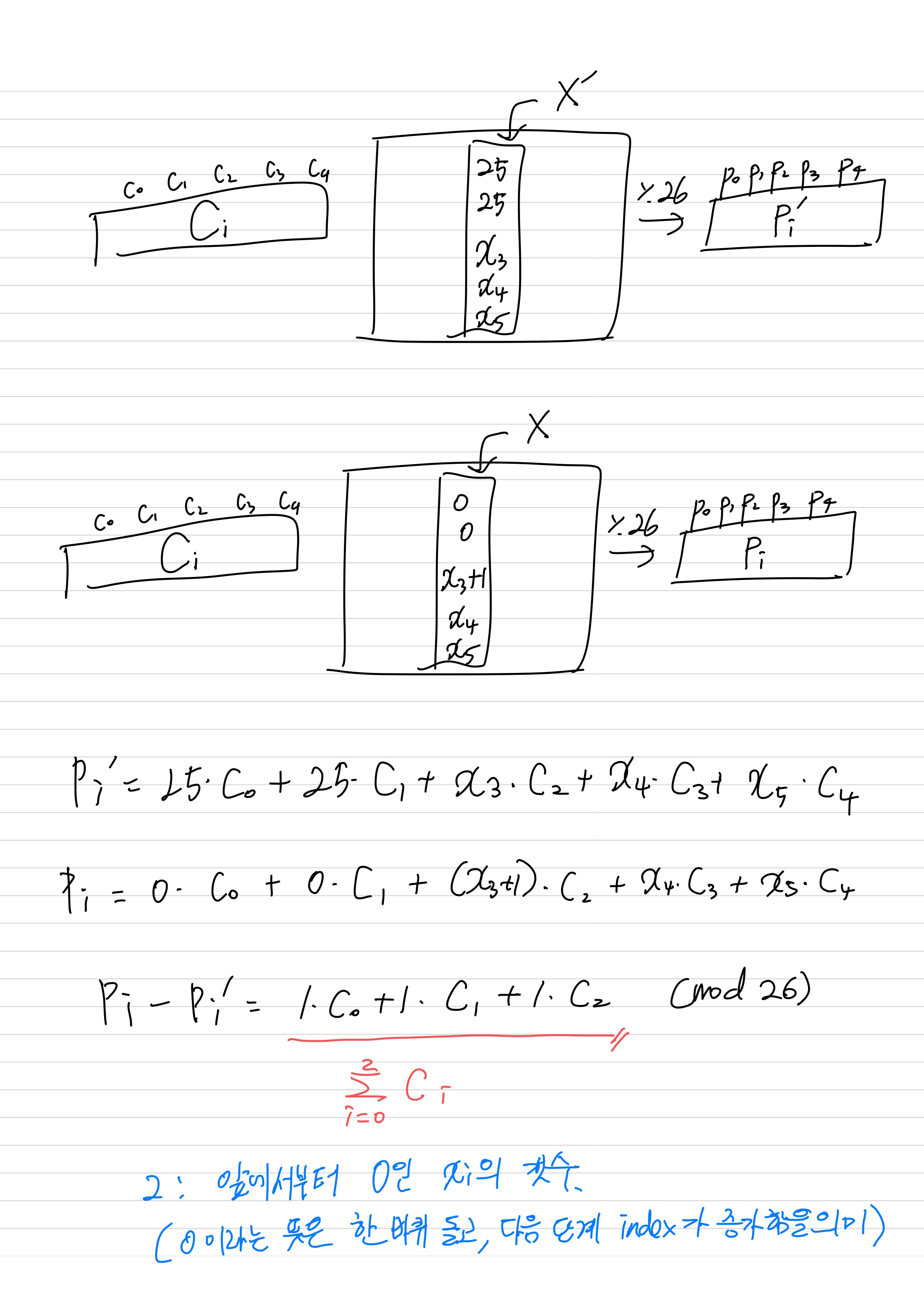
이처럼 각 열별로 (191x5 형태로 암호문을 나열했을 때) 암호문의 합을 저장해두면 시간복잡도를 줄일 수 있다.

5. 코드

import math

# len: 955 = 5 * 191
# c: cipher
c = ''
c_block = [[0 for _ in range(5)] for _ in range(191)]

# alphabet frequency
freq = [0.082, 0.015, 0.028, 0.043, 0.127, 0.022, 0.020, 0.061, 0.070, 0.002, 0.008, 0.004, 0.024, 0.067, 0.015, 0.019, 0.001, 0.060, 0.063, 0.091, 0.028, 0.010, 0.024, 0.002, 0.020, 0.001]

# 블럭 단위로 분리
for i in range(191):
    for j in range(5):
        c_block[i][j] = ord(c[5*i+j]) - ord('A')

d_arr = [[0 for _ in range(5)] for _ in range(191)]

for i in range(191):
    temp = 0
    for j in range(5):
        temp = (temp + c_block[i][j]) % 26
        d_arr[i][j] = temp

inv_key = [[1 for _ in range(5)] for _ in range(5)]
iml_arr = [9999 for _ in range(5)]
plain = [0 for _ in range(191)]

iml = -math.log2(freq[0])

for i4 in range(26):
    for i3 in range(26):
        for i2 in range(26):
            for i1 in range(26):
                for i0 in range(26):
                    l = [i0, i1, i2, i3, i4]

                    # cnt: i0~i4 중 0인 것의 갯수. 전부 0이면 pass (필요없는 키)
                    cnt = 0
                    while cnt < 5:
                        if l[cnt] != 0:
                            break
                        cnt += 1

                    if cnt != 5:
                        for i in range(191):
                            iml += math.log2(freq[plain[i]]) / 191
                            plain[i] = (plain[i] + d_arr[i][cnt]) % 26
                            iml -= math.log2(freq[plain[i]]) / 191

                    # 역행렬 존재 여부 우선판별
                    chk = 0
                    for i in l:
                        if (i % 2 != 0 and i % 13 != 0):
                            chk = 1
                            break

                    if chk == 1:
                        maxidx = 0
                        for i in range(5):
                            if iml_arr[i] > iml_arr[maxidx]:
                                maxidx = i

                        if iml_arr[maxidx] > iml:
                            iml_arr[maxidx] = iml
                            for i in range(5):
                                inv_key[i][maxidx] = l[i]

p_block = [[0 for _ in range(5)] for _ in range(191)]

for i in range(5):
    for j in range(5):
        print(inv_key[i][j], end = ' ')
    print()

for i in range(191):
    for j in range(5):
        for k in range(5):
            p_block[i][j] = (p_block[i][j] + c_block[i][k] * inv_key[k][j]) % 26

for i in range(191):
    print(chr(p_block[i][4] + ord('a')), chr(p_block[i][2] + ord('a')), chr(p_block[i][3] + ord('a')), chr(p_block[i][1] + ord('a')), chr(p_block[i][0] + ord('a')), sep='',end='')

처음에 출력을 했을 때는 하나의 행 내에서 평문이 뒤죽박죽 섞여있다. 하지만 마지막 줄에서 important라는 단어를 찾을 수 있고 이에 맞춰 열을 수정해주면 정확한 평문을 얻을 수 있다.

6. 결과

[복호화 키]

18 9 17 12 3
12 7 24 18 19
6 12 13 4 11
16 20 11 9 2
23 13 21 0 3

toy hill cipher 끝!