2022 Kakao Blind Recruitment
파괴되지 않은 건물

문제 설명
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.
적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.
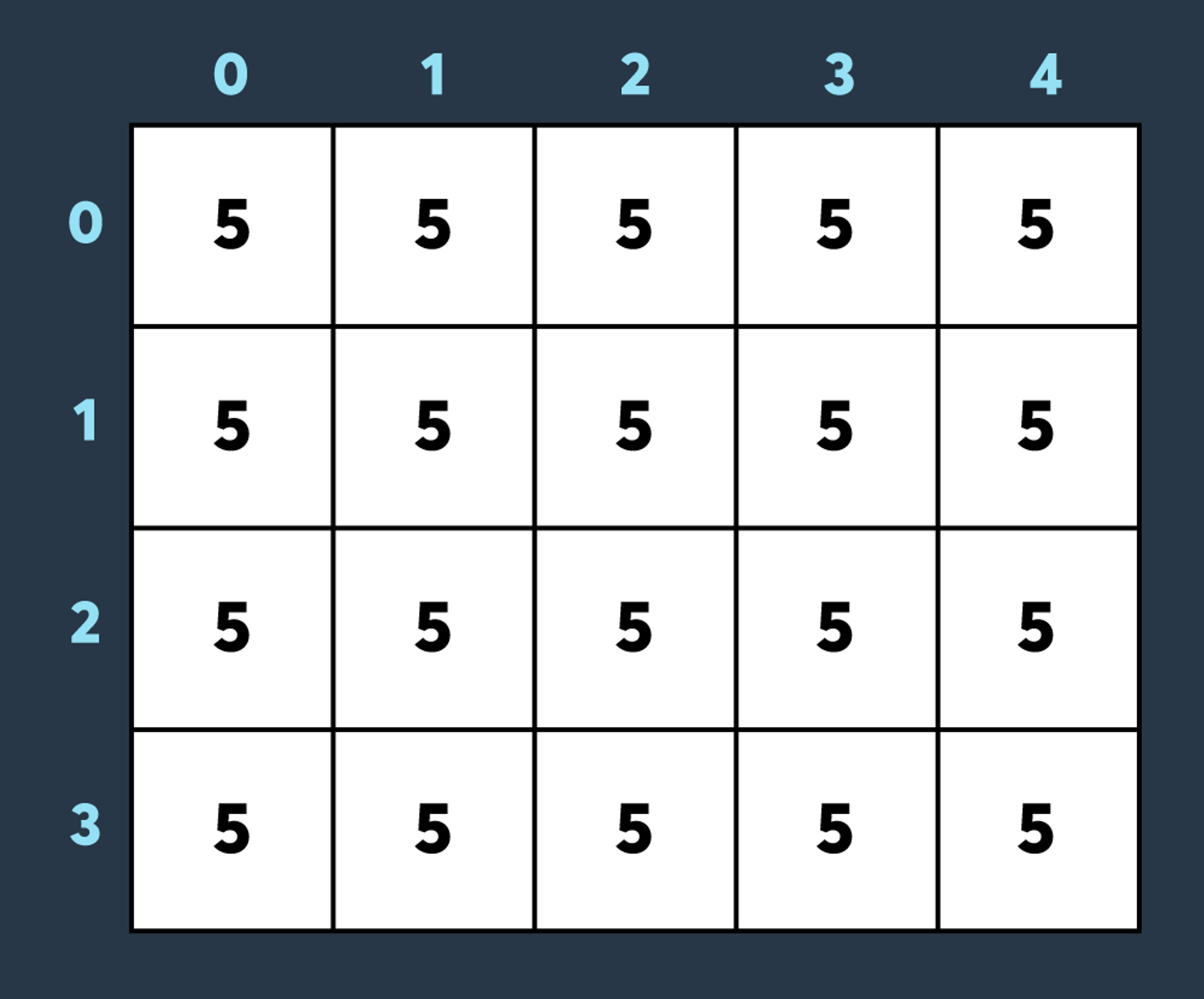
첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
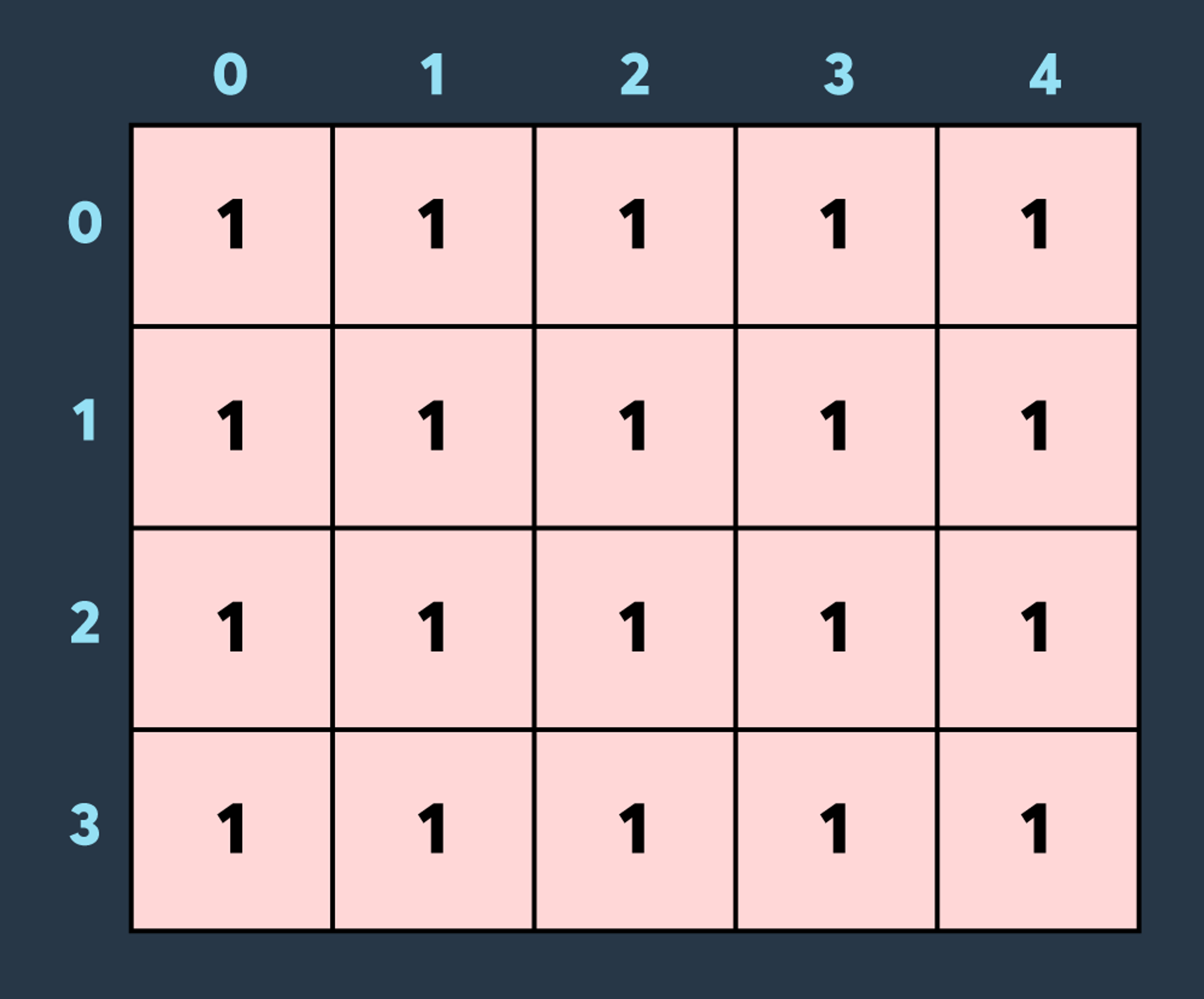
두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.
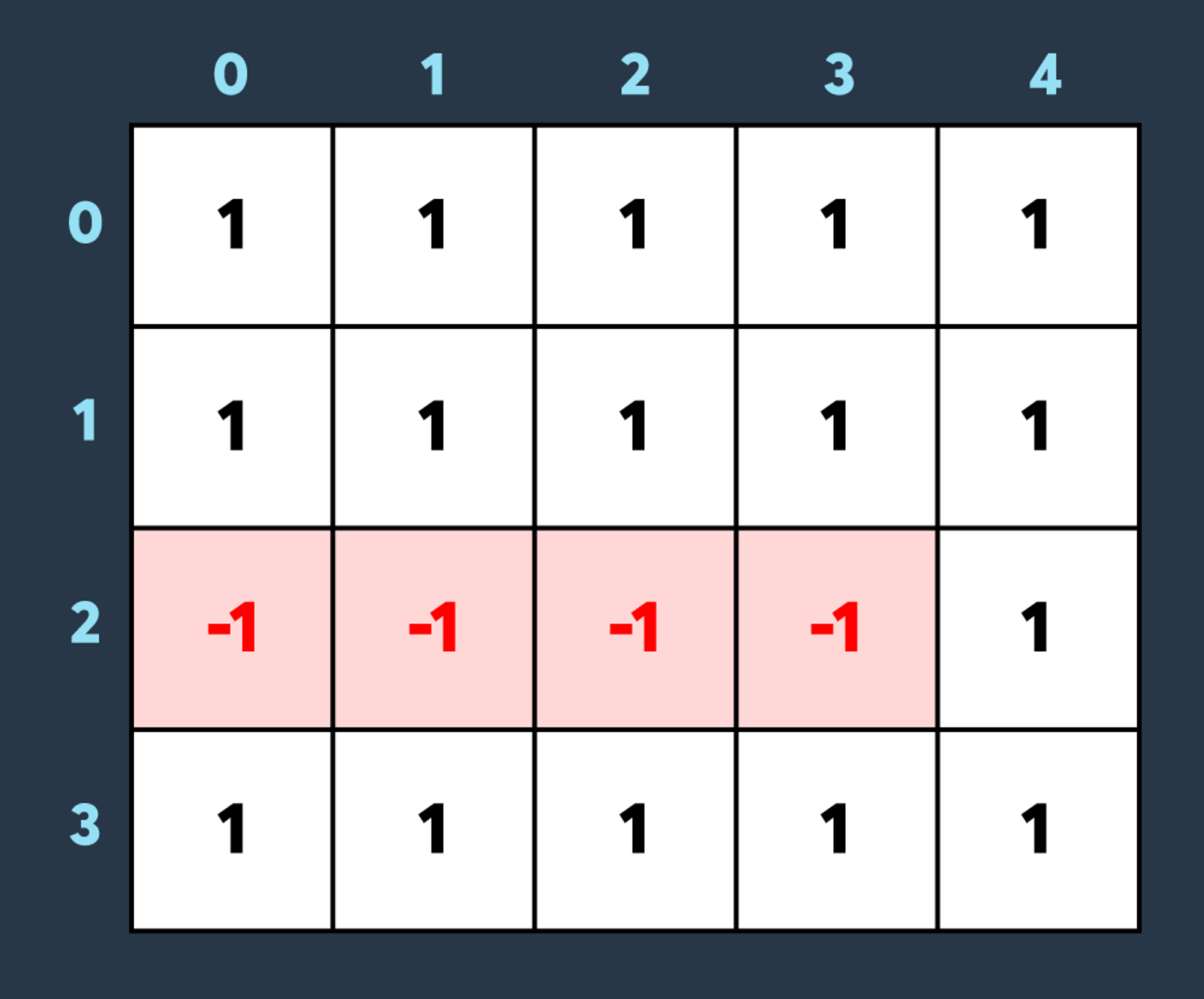
세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.
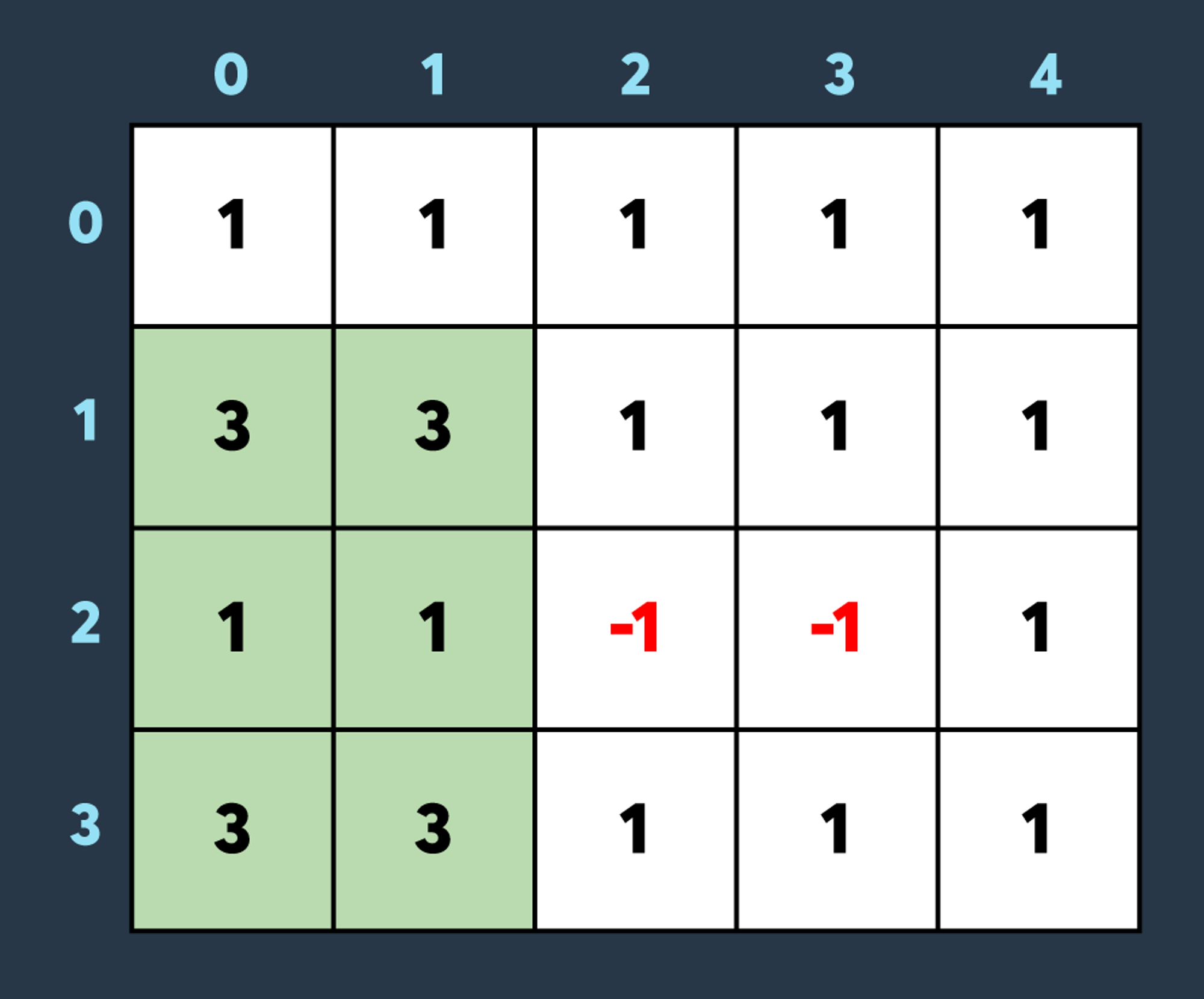
마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)
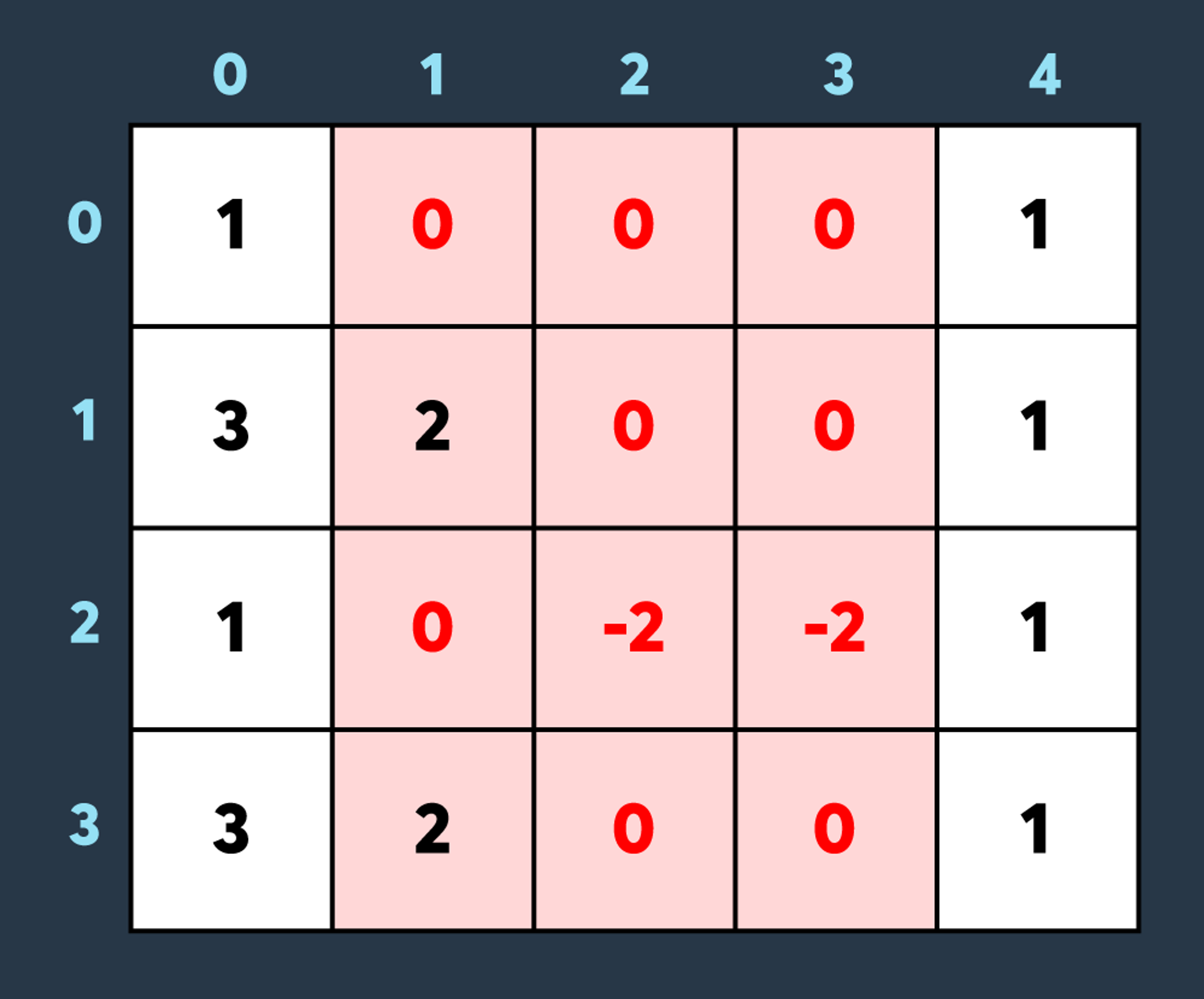
최종적으로 총 10개의 건물이 파괴되지 않았습니다.
건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.
제한 조건
- 1 ≤
board의 행의 길이 (=N) ≤ 1,000 - 1 ≤
board의 열의 길이 (=M) ≤ 1,000 - 1 ≤
board의 원소 (각 건물의 내구도) ≤ 1,000 - 1 ≤
skill의 행의 길이 ≤ 250,000 skill의 열의 길이 = 6skill의 각 행은[type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.- type은 1 혹은 2입니다.
- type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
- type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
- (r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
- 0 ≤ r1 ≤ r2 <
board의 행의 길이 - 0 ≤ c1 ≤ c2 <
board의 열의 길이 - 1 ≤ degree ≤ 500
- type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
- type이 2이면 degree만큼 건물의 내구도를 높입니다.
- 0 ≤ r1 ≤ r2 <
- type은 1 혹은 2입니다.
- 건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.
정확성 테스트 케이스 제한 사항
- 1 ≤
board의 행의 길이 (=N) ≤ 100 - 1 ≤
board의 열의 길이 (=M) ≤ 100 - 1 ≤
board의 원소 (각 건물의 내구도) ≤ 100 - 1 ≤
skill의 행의 길이 ≤ 100- 1 ≤ degree ≤ 100
효율성 테스트 케이스 제한 사항
- 주어진 조건 외 추가 제한사항 없습니다.
입출력 예
| board | skill | result |
|---|---|---|
| [[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5]] | [[1,0,0,3,4,4],[1,2,0,2,3,2],[2,1,0,3,1,2],[1,0,1,3,3,1]] | 10 |
| [[1,2,3],[4,5,6],[7,8,9]] | [[1,1,1,2,2,4],[1,0,0,1,1,2],[2,2,0,2,0,100]] | 6 |
입출력 예 설명
입출력 예 #1
문제 예시와 같습니다.
입출력 예 #2
<초기 맵 상태>
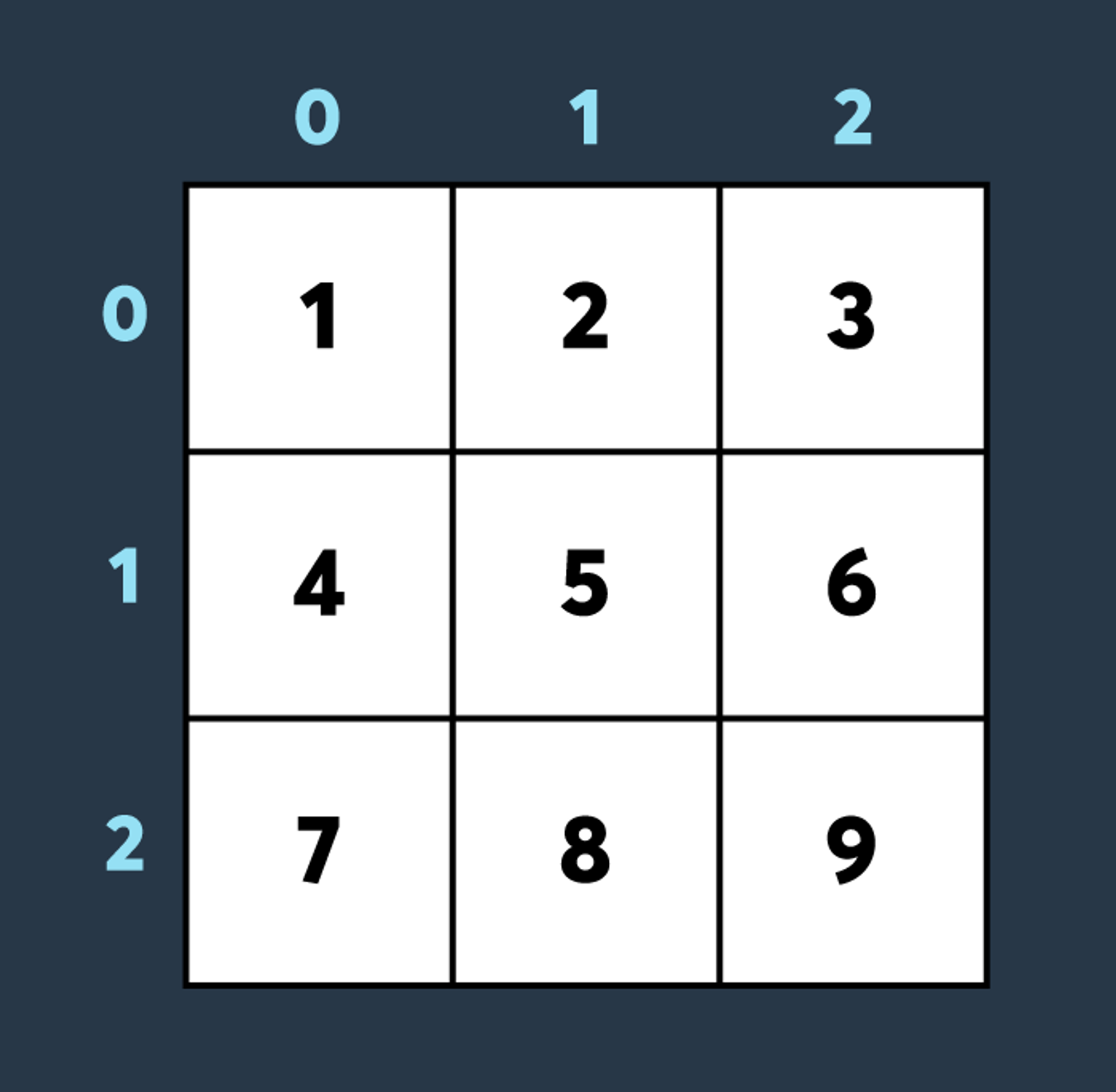
첫 번째로 적이 맵의 (1,1)부터 (2,2)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
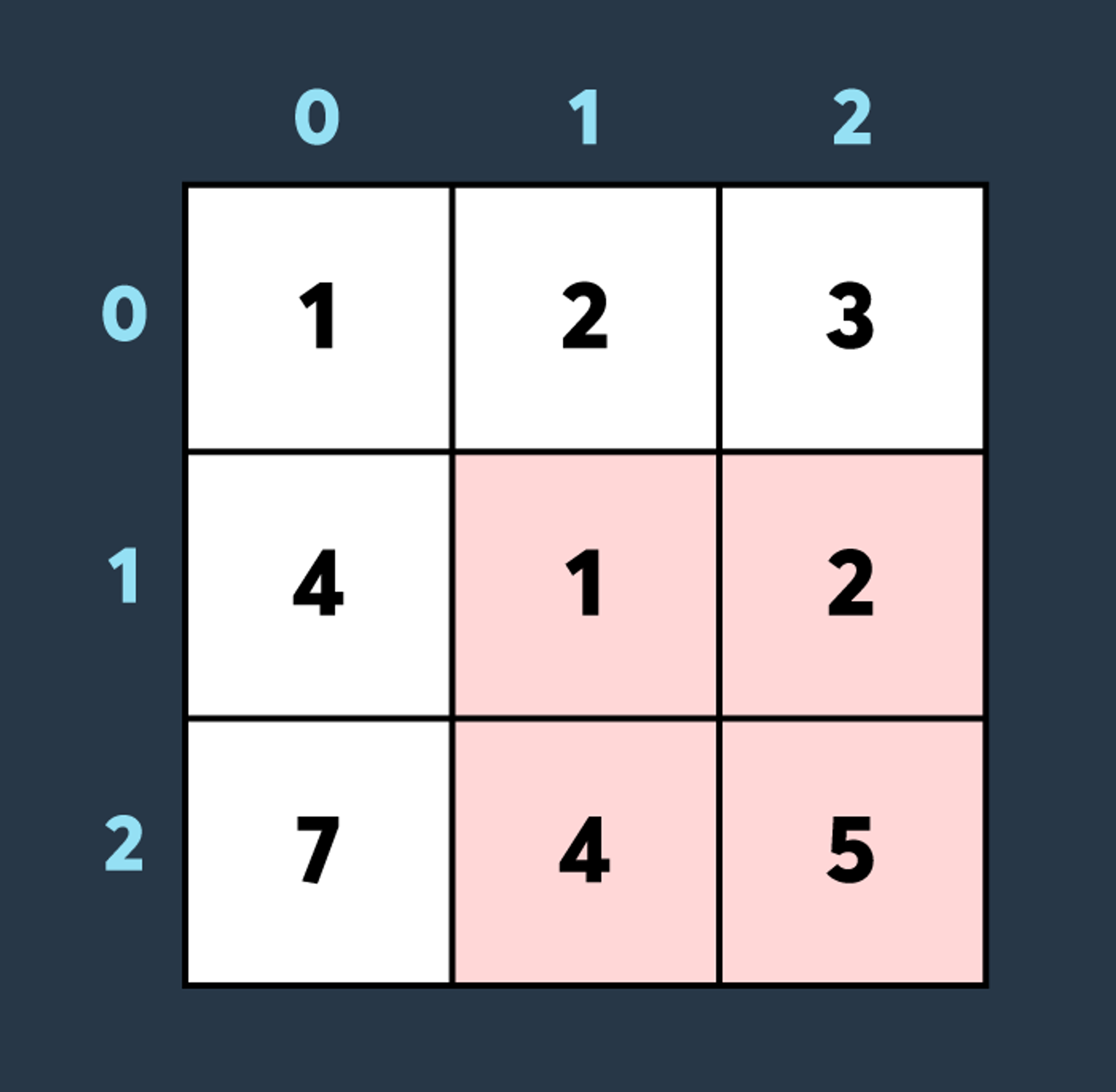
두 번째로 적이 맵의 (0,0)부터 (1,1)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
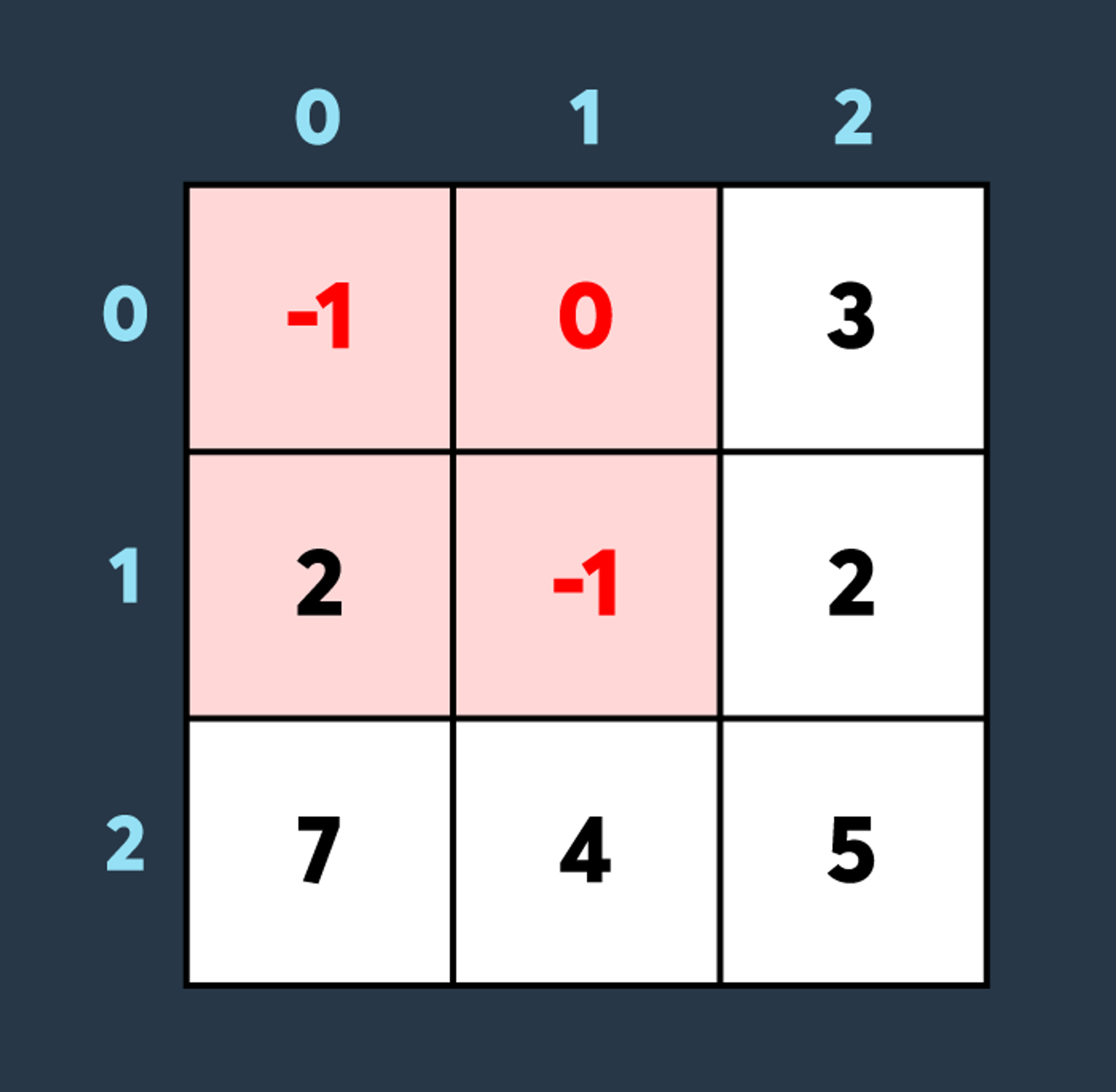
마지막으로 아군이 맵의 (2,0)부터 (2,0)까지 회복하여 100만큼 건물의 내구도를 높이면 아래와 같은 상황이 됩니다.
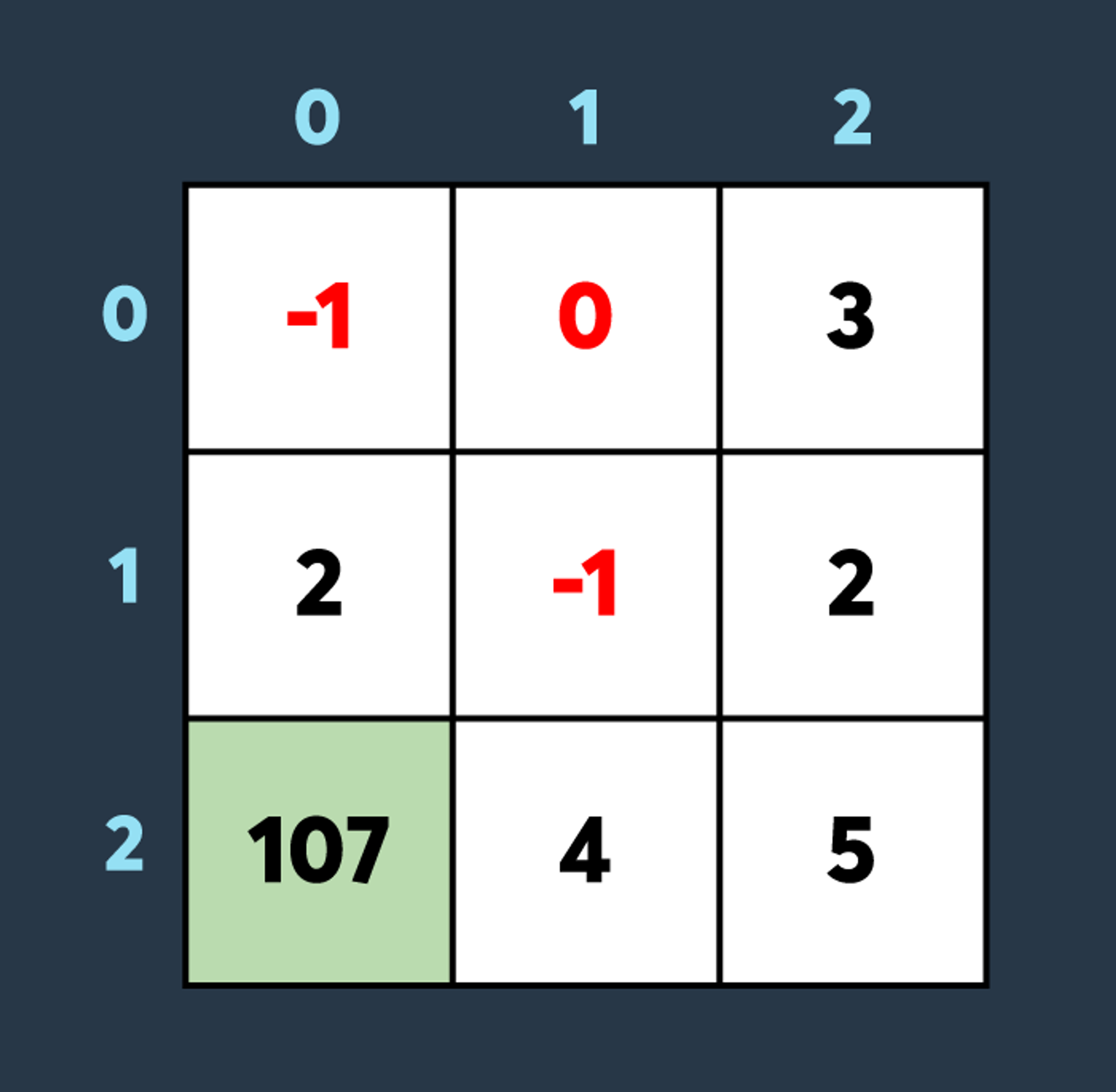
총, 6개의 건물이 파괴되지 않았습니다. 따라서 6을 return 해야 합니다.
첫번째 풀이 과정
- 데미지를 주는 함수를 만들고 회복을 해주는 함수를 만든다
- 반복문을 사용하여 skill 배열을 하나하나 검사하여 반복문을 또 사용하여 board 에 반영
첫번째 풀이
let board = [
[5, 5, 5, 5, 5],
[5, 5, 5, 5, 5],
[5, 5, 5, 5, 5],
[5, 5, 5, 5, 5],
];
let skill = [
[1, 0, 0, 3, 4, 4],
[1, 2, 0, 2, 3, 2],
[2, 1, 0, 3, 1, 2],
[1, 0, 1, 3, 3, 1],
];
// 피해를 입히는 함수
const dam = (a, startIndex, distance, damage) => {
for (let i = startIndex; i <= startIndex + distance; i++) {
board[a][i] = board[a][i] - damage;
}
};
//회복해주는 함수
const heal = (a, startIndex, distance, damage) => {
for (let i = startIndex; i <= startIndex + distance; i++) {
board[a][i] = board[a][i] + damage;
}
};
//skill을 하나하나 검사하고 반영
for (let i = 0; i < skill.length; i++) {
let howFar = skill[i][4] - skill[i][2];
if (skill[i][0] == 1) {
for (let j = skill[i][1]; j <= skill[i][3]; j++) {
dam(j, skill[i][2], howFar, skill[i][5]);
}
} else if (skill[i][0] == 2) {
for (let j = skill[i][1]; j <= skill[i][3]; j++) {
heal(j, skill[i][2], howFar, skill[i][5]);
}
}
}
//0이상은 숫자를 확인하여 더해줌
for (let i = 0; i < board.length; i++) {
for (let j = 0; j < board[0].length; j++) {
if (board[i][j] > 0) {
result++;
}
}
}문제 발생
정확도 테스트는 통과 하였으나, 효율성 테스트에서 실패함
반복문을 너무 많이 돌려서 그런 것 같음.
IMOS 알고리즘
출처 - https://nicotina04.tistory.com/163
선분에서의 imos법
특정 구간에 1을 더하길 원한다고 해보자.
imos법은 구간이 시작되는 점에 1을 더하고 구간을 벗어나는 가장 첫 번째 점에 1을 뺀 뒤 이 사이를 누적합으로 더해가며 스위핑 한다.
위에서 말한 대로 스위핑을 하면 해당 구간에 1을 더한 결과를 얻을 수 있다.
1부터 5까지 1을 더하는 예시를 보도록 하자.
| 1 | 0 | 0 | 0 | 0 | -1 |
|---|
범위가 1 이상 5 이하이므로 구간의 시작인 1에 1을 더하고 구간을 벗어나는 첫 번째 점인 6에 1을 뺀 상태이다.
2부터 6까지 ar[i]=ar[i]+ar[i−1]ar[i]=ar[i]+ar[i−1]을 해가며 스위핑을 해보자.
| 1 | 1 | 1 | 1 | 1 | 0 |
|---|
보다시피 1~5 범위의 구간이 모두 1로 채워진 것을 확인할 수 있다.
구간을 더하는 쿼리만 있을 때 imos법을 사용하면 구간에 1을 더하는 쿼리가 몇 개, 아니 몇천만 개가 들어오던지 간에 O(N)O(N)으로 해결할 수 있는 강력한 알고리즘이다.
imos법으로 2차원 직교 좌표계에서 사각형 채우기
물론 imos법은 2차원 도형을 채울 때도 그 위력을 발휘한다.
이번엔 2차원 좌표계에서 사각형을 채우는 법을 알아보자.
3*3 사각형을 완성하고자 할 때는 다음과 같이 수를 채워야 한다.
| 1 | -1 | ||
|---|---|---|---|
| -1 | 1 |
모든 행에 대해 오른쪽으로 스위핑을 하면
| 1 | 1 | 1 | 0 |
|---|---|---|---|
| -1 | -1 | -1 | 0 |
그다음 모든 열에 대해 아래쪽으로 스위핑을 하면
| 1 | 1 | 1 | 0 |
|---|---|---|---|
| 1 | 1 | 1 | |
| 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 |
이렇게 O(N2) O(N2)로 사각형을 완성할 수 있다.
풀이 과정
- IMOS 를 이용하여 skill 을 하나의 배열로 만들어서 저장
- 원래 배열 board 에 저장한 배열을 더한다.
- 0 이상인 값 계산
IMOS 이용한 풀이
function solution(board, skill) {
// board 보다 행과 열이 1 씩 더 큰 배열 생성
let newArr = Array.from({ length: board.length + 1 }, () =>
Array(board[0].length + 1).fill(0)
);
//IMOS 알고리즘을 이용하여 skill을 모두 하나의 배열에 저장
for (let i = 0; i < skill.length; i++) {
let first = skill[i][0] === 1 ? -1 : 1;
newArr[skill[i][1]][skill[i][2]] += skill[i][5] * first;
newArr[skill[i][1]][skill[i][4] + 1] += skill[i][5] * first * -1;
newArr[skill[i][3] + 1][skill[i][2]] += skill[i][5] * first * -1;
newArr[skill[i][3] + 1][skill[i][4] + 1] += skill[i][5] * first;
}
//위에서 아래로 거듭합
for (let i = 0; i < board.length; i++) {
for (let j = 0; j < board[0].length; j++) {
newArr[i + 1][j] += newArr[i][j];
}
}
//좌에서 우로 거듭합
for (let i = 0; i < board.length; i++) {
for (let j = 0; j < board[0].length; j++) {
newArr[i][j + 1] += newArr[i][j];
}
}
// 0보다 큰 앖을 저장
let cnt = 0;
//board 배열에 newArr 값을 더함
for (let i = 0; i < board.length; i++) {
for (let j = 0; j < board[0].length; j++) {
if ((board[i][j] += newArr[i][j]) > 0) {
cnt++;
}
}
}
return cnt;
}