Delegation

USACO 2020 Feb Gold 3

Problem

Solution

Yes, it is a Gold 3, but no need to fret! Let's start with some trivial test cases provided by the problem. How can we solve the problem when the graph forms a star?

Let vertex $v$ be the root of the star, and $d_i$ be the number of edges in each branch. Trivially, $K|N$, and to go even further, if $M_i$ is the number of $d$ such that $d \equiv i (mod K)$, $M_i=M_{K-i} (1\le i \le K-1)$. If not, the partition is not possible because elements in $M_i$ has to be paired with $M_{K-i}$ and vice versa.

Let's combine this property with tree DP. We can define $dp[i]$ as following.

$dp[i]=\text{Check if subtree of i can be partitioned}$

Even though the subtree itself may not be partitioned, it can be redeemed further up in the the tree as vertex 8 does in the following figure.

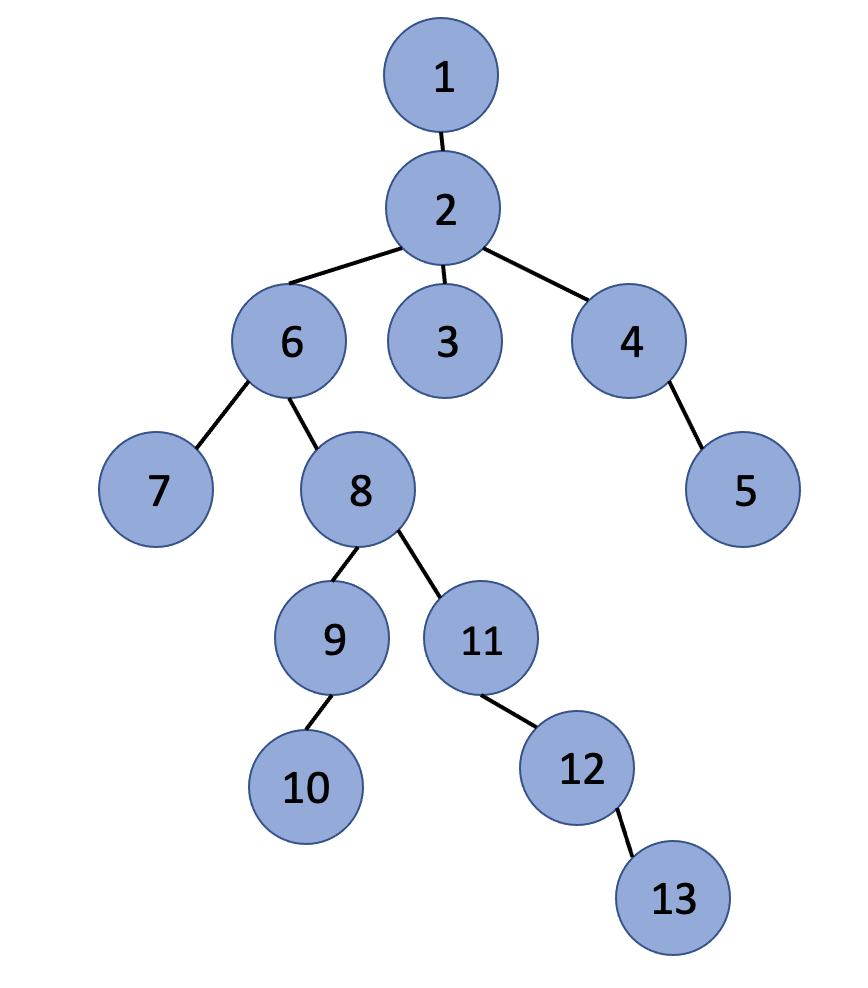
As seen in the figure, $dp[8]$ will return 2 but this 2 will be later solved in $dp[6]$ by the edge between 6 and 8.

I used multiset to implement the solve function of DP (not sure if this is the ideal approach since it is risky for TLE).

Code

#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <set>
using namespace std;
int N, dp[100010], K, ans[100010], mark[100010];
vector <int> graph[100010], son[100010];
int solve(int x){
    multiset<int> s;
    int &r=dp[x];
    if(r!=-1) return r;
    else{
        r=0;
        for(int nxt : son[x]){
            if(solve(nxt)==-2){
                r=-2;
            }
            else{
                int val=(1+solve(nxt))%K;
                if(val!=0){
                    if(s.count(K-val)>0)
                        s.erase(s.find(K-val));
                    else s.insert(val);
                }
            }
        }
        if(r!=-2){
            if(s.size()==0) r=0;
            else if(s.size()==1) r=*s.begin();
            else r=-2;
        }
    }
    return r;
}
void dfs(int v){
    mark[v]=1;
    for(int nxt : graph[v])
        if(mark[nxt]==0){
            son[v].push_back(nxt);
            dfs(nxt);
        }
}
int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> N;
    for(int i=1; i<N; i++){
        int u, v;
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u);
    }
    dfs(1);
    for(int i=1; i<N; i++){
        if((N-1)%i!=0){
            ans[i]=0;
            continue;
        }
        K=i;
        fill(&dp[0], &dp[100010], -1);
        solve(1);
        
        if(dp[1]==0)
            ans[i]=1;
        else ans[i]=0;
    }
    for(int i=1; i<N; i++)
        cout << ans[i];
    
    return 0;
}