Water

POI 1998/1999 Stage 3 P6

Problem

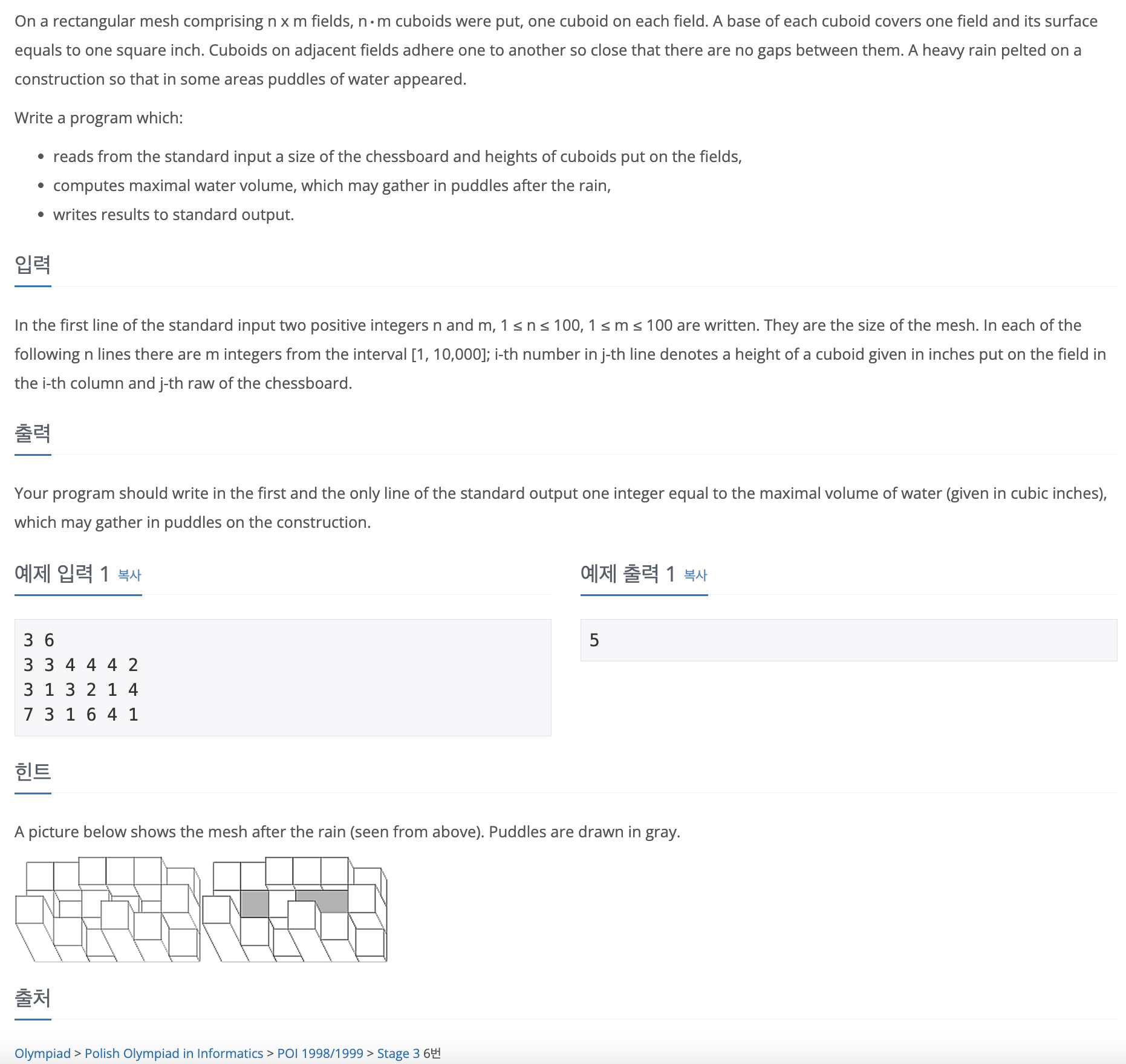
Solution

Pretty challenging problem, I would say because it is hard to think of the logically correct approach. How can we interpet "water being filled into the mesh" mathematically. Well if you think about the condition in which the water flows outside, there should exist a decreasing sequence of heights that will bring the water outside (ex. 4-4-3-2-1-0). The water can be filled if there's somewhat a bottleneck that can stop the water from flooding (like in 4-4-7-3-2-1-0, the 7 will trap the water)

The mathematical interpretation of the "max height of water being filled" is the min of max of each paths leading to 0.

The min of max of each paths leading to 0 can be found using dp, since the min of max depends the min of max of the adjacent nodes as well. We just need to carefully determine the order in which the dp values will be set, using min priority queue.

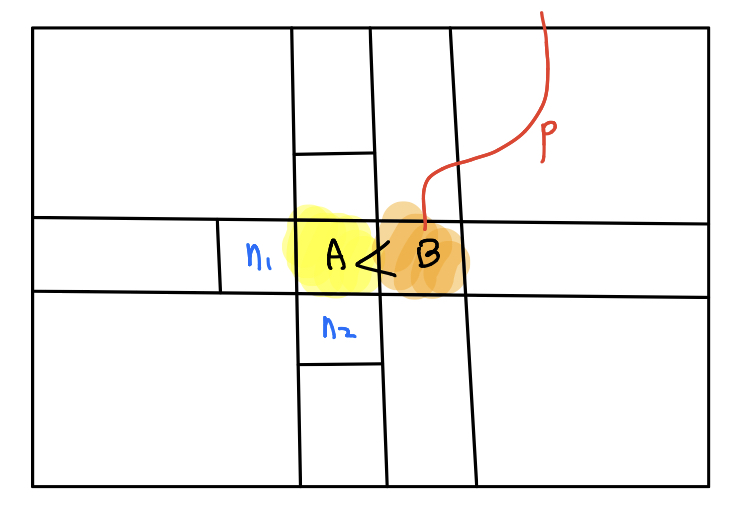
Assume $B$ is the next target, derived from the current top of the priority queue $A$. If there exists another path $p$ such that the max of $p$ is smaller than the value derived from $A$, note that $A$ value is smaller than $B$ value since it came out first in the priority queue. Therefore, the max of $p$ should be the dp value for $A$ as well. Contradiction (Doesn't this remind of us Dijkstra?).

Code

#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
int N, M, board[110][110], sum, wsum, mark[110][110];
int dx[4]={1,-1,0,0}, dy[4]={0,0,1,-1};
struct Data{
    int x, y, h;
};
bool cmp(Data &a, Data&b){
    return a.h>b.h;
}
//priority_queue syntax!
priority_queue<Data, vector<Data>, decltype(&cmp)> pq(&cmp);
int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> N >> M;
    for(int i=1; i<=N; i++){
        for(int j=1; j<=M; j++){
            cin >> board[i][j]; sum+=board[i][j];
            if(i==1){
                pq.push({i,j,board[i][j]});
                mark[i][j]=board[i][j];
            }
            else if(i==N){
                pq.push({i,j, board[i][j]});
                mark[i][j]=board[i][j];
            }
            else if(j==1 || j==M){
                pq.push({i,j,board[i][j]});
                mark[i][j]=board[i][j];
            }
        }
    }
    while(!pq.empty()){
        auto cur=pq.top(); pq.pop();
        int x=cur.x, y=cur.y, h=cur.h;
        wsum+=mark[x][y];
        for(int i=0; i<4; i++){
            int nx=x+dx[i], ny=y+dy[i];
            if(1<=nx && nx<=N && 1<=ny && ny<=M){
                if(mark[nx][ny]==0){
                    mark[nx][ny]=max(board[nx][ny], mark[x][y]);
                    pq.push({nx, ny, mark[nx][ny]});
                }
            }
        }
        
    }
    cout << wsum-sum;
    return 0;
}