Paleta

COCI 2013/2014 Contest 2 P5

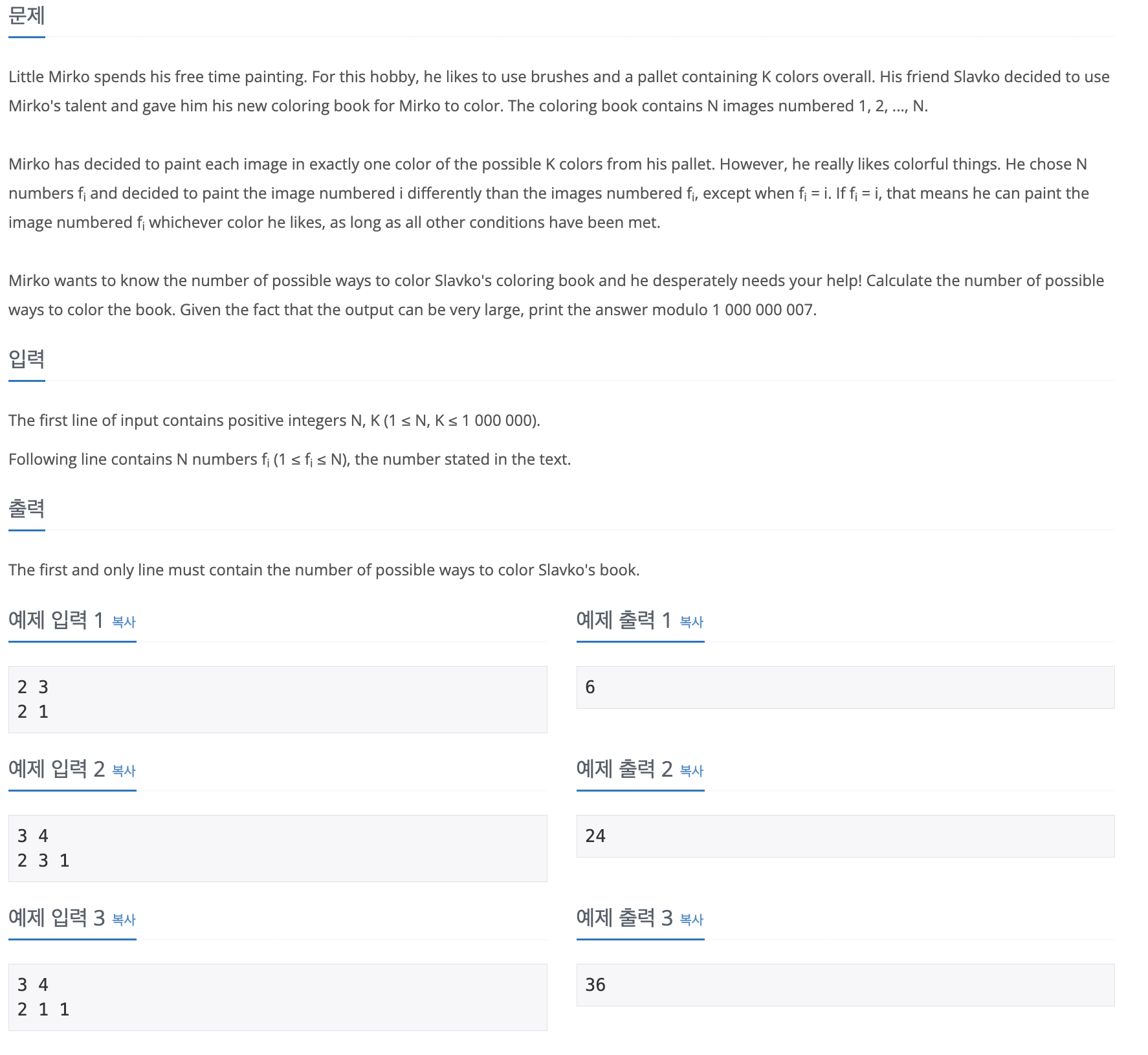
Problem

Solution

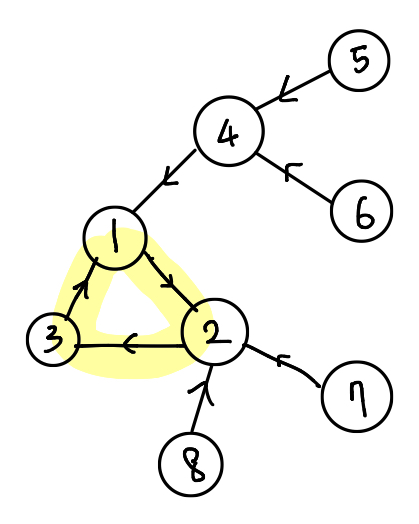
Great combination of math and coding! Here we encounter the concept called functional graph, where each node has exactly one out-edge. In functional graphs, for each connected components, there exists exactly one cycle, and the other edges are heading into the cycle, connected (see figure for better understanding).

Therefore, for each connected components, which we can get using dfs, we can start counting the number of possible coloring and get the product of each values. This is where dp comes in.

Let $a_n$ be the number of ways to color the cycle of length $n$. If there are $k$ colors, $a_n=k\cdot(k-1)^{n-1}-a_{n-1}$ ( Pretty well-known in MO).

Then for the branches coming into the cycle, the number of ways if the power of $k-1$.

Code

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
long long N, K, nxt[1000010], mark[1000010], cycle[1000010], cc[1000010], cnt, ans=1, dp[1000010];
const long long MOD=1e9+7;
vector <long long> path;
long long power(long long base, long long exp){
    if(exp==0) return 1;
    long long temp=power(base, exp/2);
    if(exp%2==0) return (temp*temp)%MOD;
    else return ((temp*temp)%MOD*base)%MOD;
}
void dfs(long long v){
    mark[v]=cnt;
    path.push_back(v);
    long long u=nxt[v];
    if(mark[u]>0){
        if(mark[u]==cnt){
            long long idx=-1;
            for(long long i=0; i<path.size(); i++){
                if(path[i]==u)
                    idx=i;
            }
            cc[cnt]+=path.size();
            cycle[cnt]+=path.size()-1-idx+1;
        }
        else if(mark[u]<cnt){
            cnt--;
            cc[mark[u]]+=path.size();
            for(long long i=0; i<path.size(); i++)
                mark[path[i]]=mark[u];
        }
    }
    else{
        dfs(u);
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> N >> K;
    for(long long i=1; i<=N; i++){
        long long v; cin >> v;
        nxt[i]=v;
    }
    for(long long i=1; i<=N; i++){
        if(mark[i]==0){
            cnt++;
            path.clear();
            dfs(i);
        }
    }
    dp[1]=K; dp[2]=K*(K-1);
    for(int i=3; i<=N; i++){
        dp[i]=(K*power(K-1, i-1)-dp[i-1])%MOD;
    }
    for(long long i=1; i<=cnt; i++){
        long long c=1;
        c=dp[cycle[i]]*power(K-1, cc[i]-cycle[i]);
        c%=MOD;
        ans*=c;
        ans%=MOD;
    }
    cout << ans;
    return 0;
}