1 Perceptron

A Perceptron is an algorithm for supervised learning of binary classifiers.
: 이진 분류기의 지도학습을 위한 알고리즘

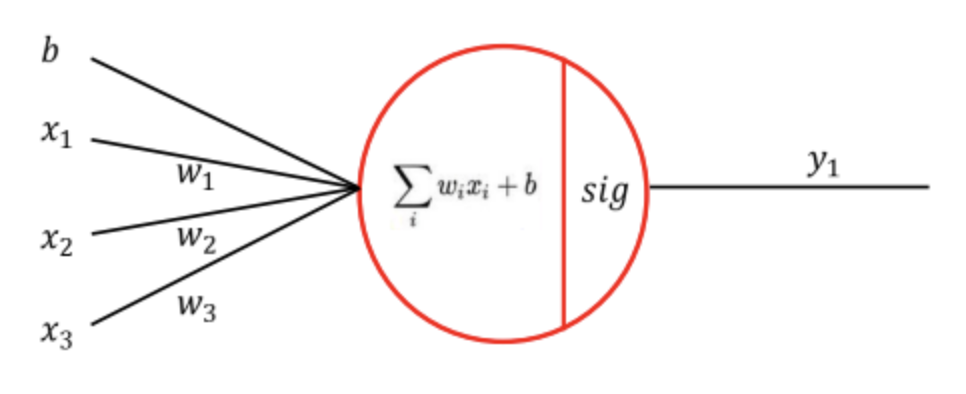
• 가중치는 정답과 예측의 차이(오차)에 비례하여 바뀜
• 퍼셉트론 1개는 하나의 output 가짐, 여러 개를 분류하려면 퍼셉트론도 여러 개 필요

2 Biological / Artificial Neural Network

🧑🏻‍🏫

Hebb rule

시냅스 양쪽의 뉴런이 동시에, 반복적으로 활성화되었다면 그 두 뉴런 사이의 연결강도가 강화된다.
⇒ 뉴런의 각 파트에 따라 특성이 달라짐

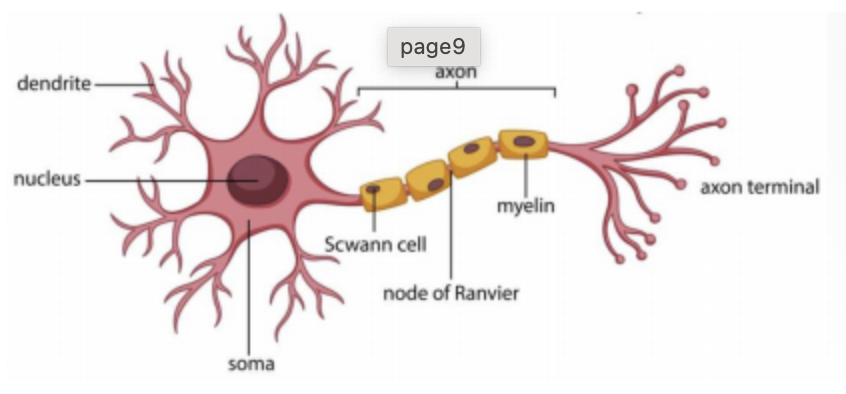
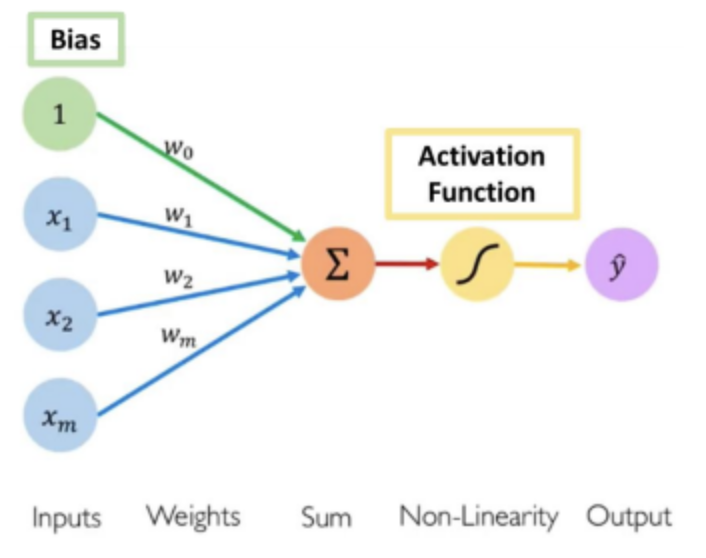
Biological NN	Artificial NN
Neuron	Perceptron
Dendrite	Input
Axon	Output
Synapse strength	Weight

---

ANN 간단한 예제

• 활성화 함수가 없는 단일 퍼셉트론

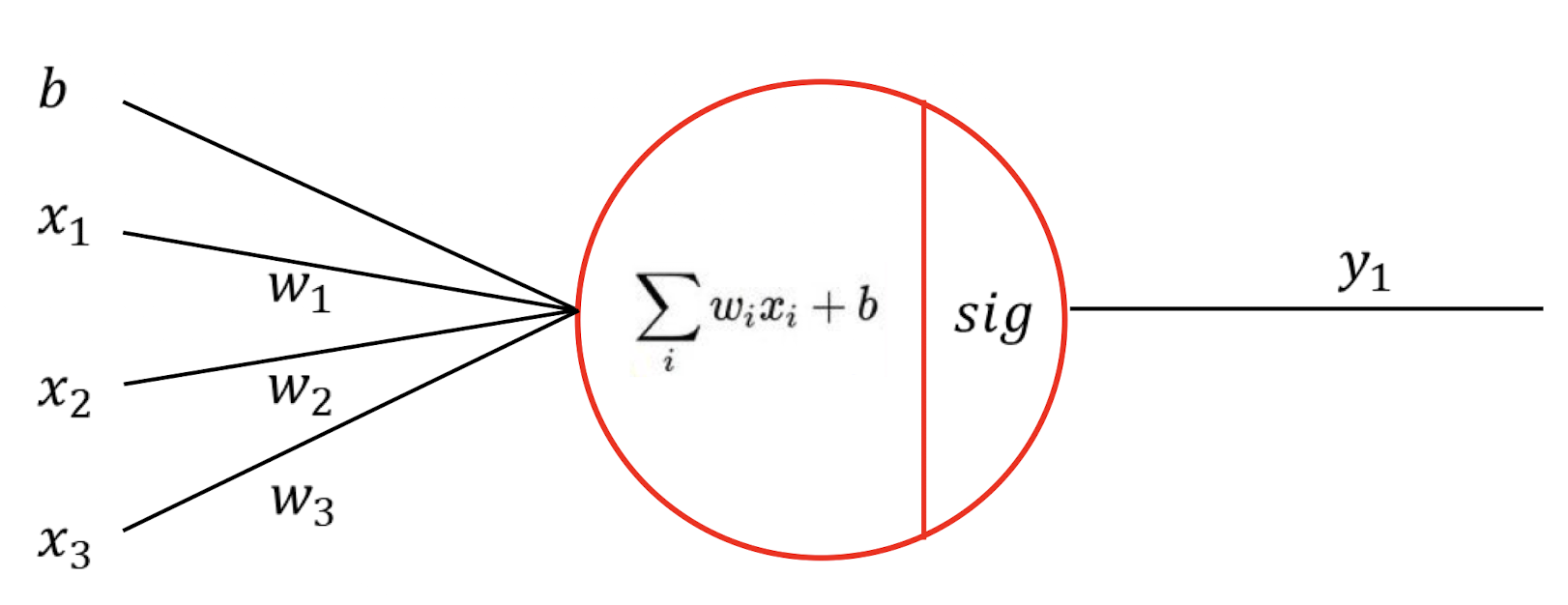
이 네트워크를 식으로 표현하면?

$y_1 = w_1x_1 + w_2x_2 + w_3x_3 + b$ ⇒ 그냥 regression과 동일

이 네트워크를 행렬 형식으로 표현하면? ( $XW=Y$ )

$\begin{bmatrix}
x_1 & x_2 & x_3 & 1
\end{bmatrix}
\begin{bmatrix}
w_1
\w_2

\w_3 \b\end{bmatrix}

\begin{bmatrix}
y_1
\end{bmatrix}$

perceptron이 하나 더 늘어난다면?

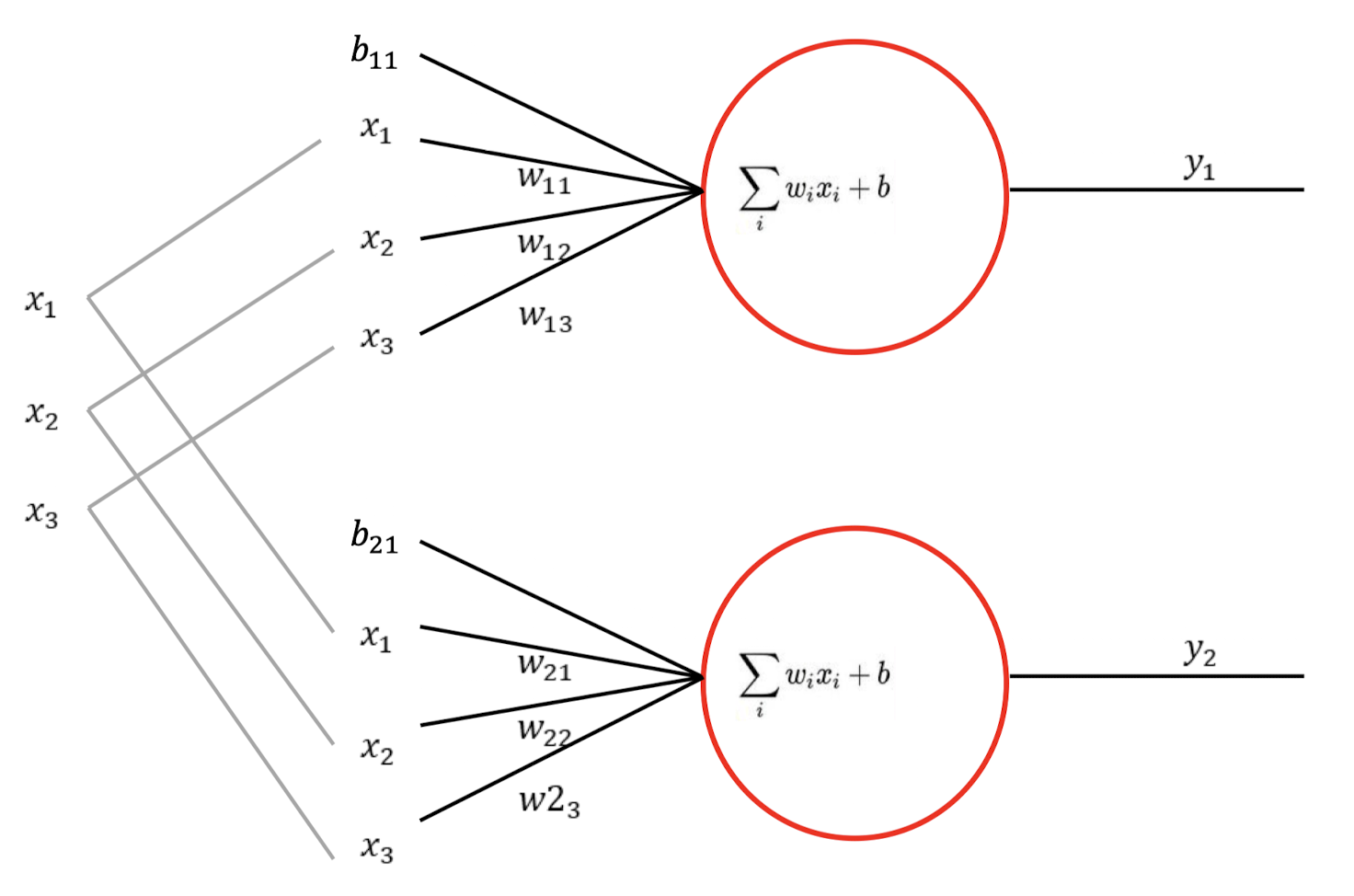
• input은 동일
• weight 수가 많아지므로 연산량도 늘어남
• 행렬의 각 열은 하나의 퍼셉트론 의미

$\begin{bmatrix}
x1 & x_2 & x_3 & 1
\end{bmatrix}
\begin{bmatrix}
w{11} & w{21} \
w{12} & w{22} \
w{13} & w{23} \
b{11} & b_{21}

\end{bmatrix}

\begin{bmatrix}
y_1 & y_2
\end{bmatrix}$

---

NN 간단 과정

1. weight, bias등 파라미터의 초기값 설정
2. cost 확인 (cost function 사용)
3. 역전파를 통해 파라미터 수정
4. 오차가 threshold보다 작아질 때까지 과정 반복

---

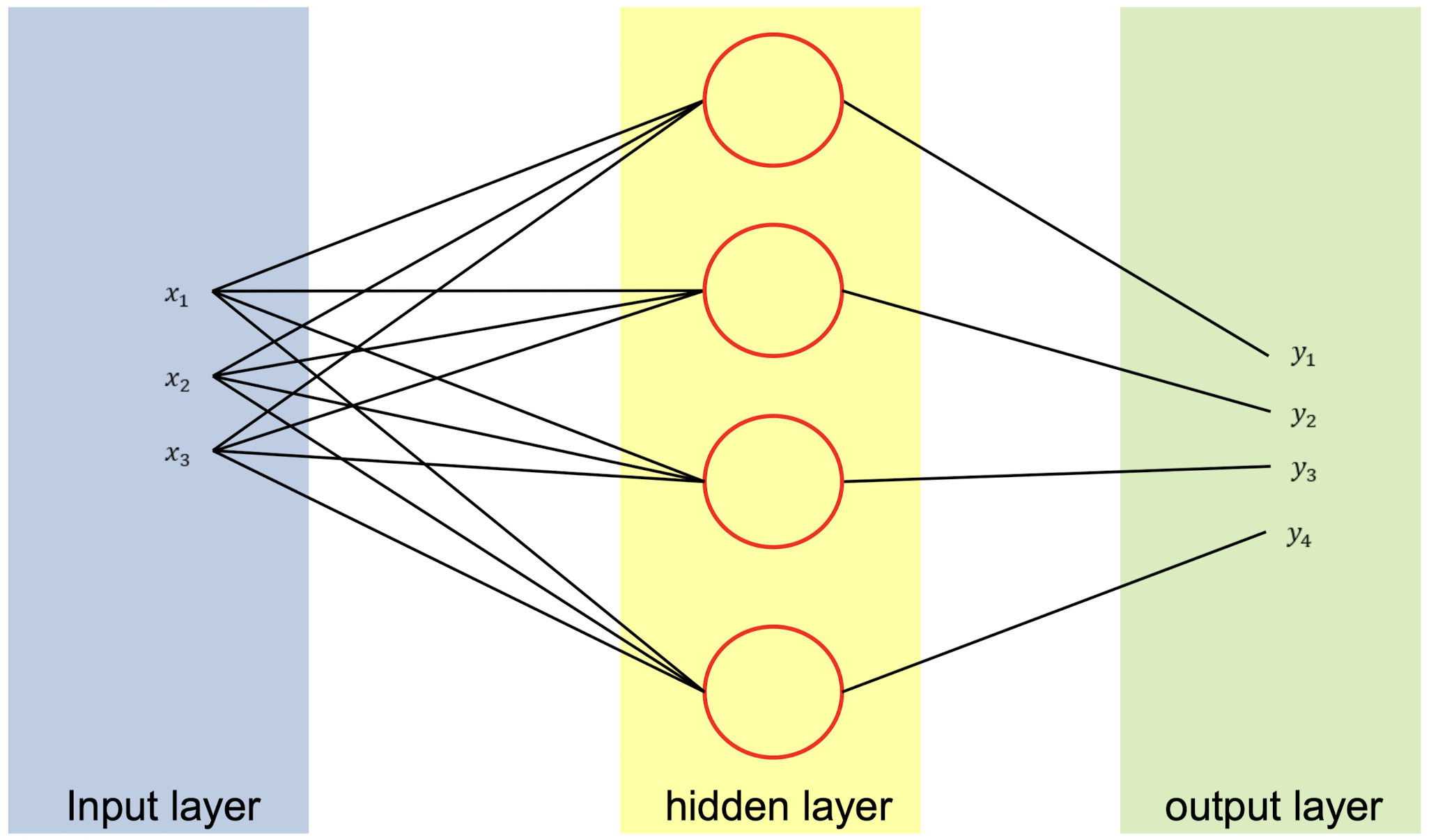
3 Multi-layered neural network

• 퍼셉트론이 있는 곳이 hidden layer
• hidden layer가 2개 이상 있는 것을 Deep learning이라고 한다.

---

4 Deep learning

NN과 ANN의 차이를 만들 무언가 필요

• one-hot encoding
• softmax
• activation function

One-hot encoding

가장 높은 확률을 1로, 나머지는 0으로 설정

4.1 Softmax

🧑🏻‍🏫

• G.T의 각 값은 one-hot encoding을 나타냄

• 따라서, 우리는 네트워크의 결과를 확률로 매치해야 함

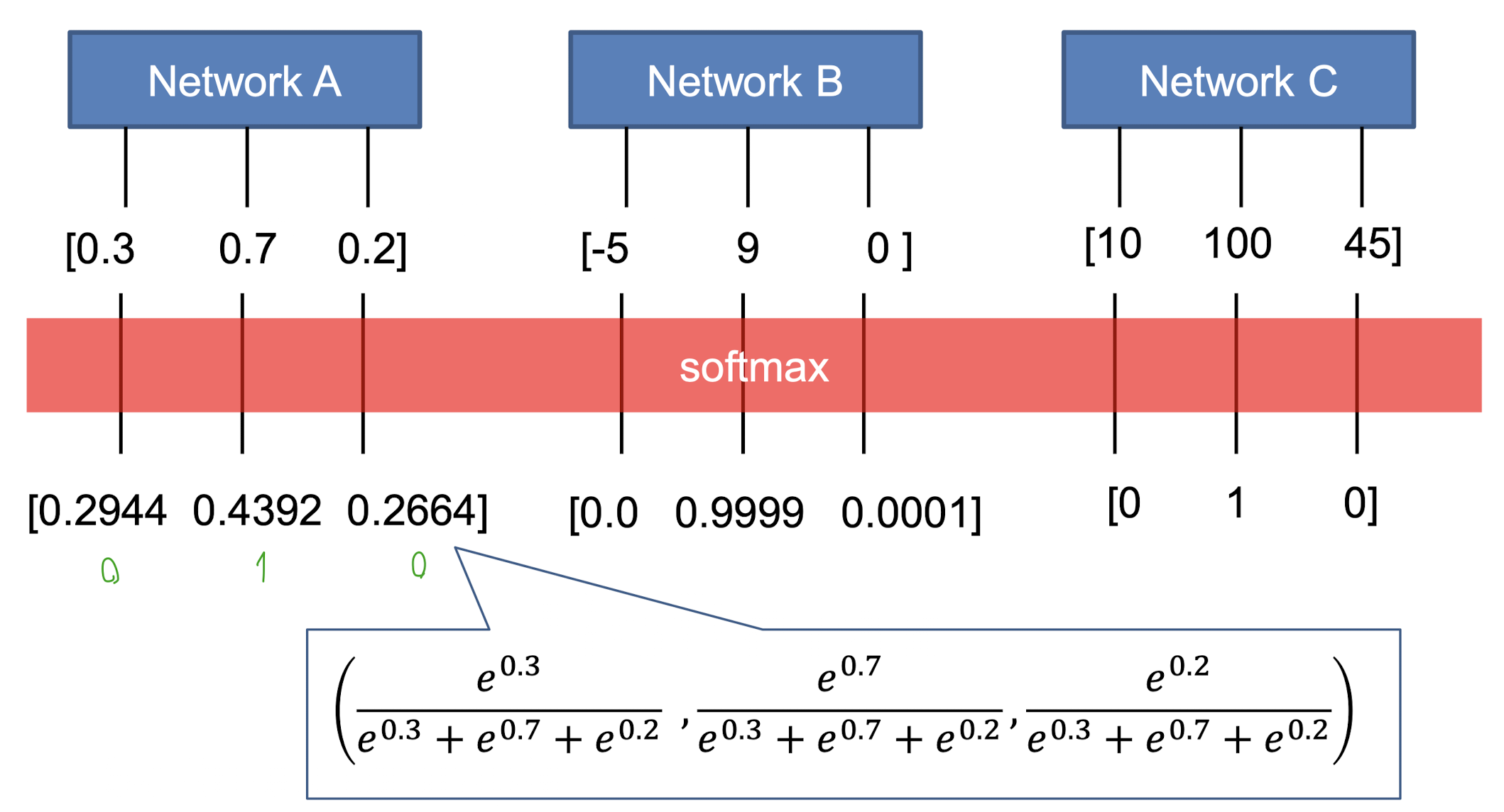
• 결과값을 확률로 변환하는 걸 ‘Softmax’라고 함

output을 확률(합이 1)로 나타낼 때, 보통 증가하는 함수를 사용

---

예제

Original output: $y = \begin{bmatrix} 0.3 & 0.7 & 0.2 \end{bmatrix}$

함수로 $y'=2^y$ 사용

New output: $y' = \begin{bmatrix} 1.2311 & 1.6245 & 1.1487 \end{bmatrix}$

$P(y') = \frac{y'_i}{\sum_{j=1}^{3} y'_j} = [0.3075 \quad 0.4057 \quad 0.2869]$

---

왜 softmax function으로 지수함수를 쓰는가?

⇒ Bayes 정리와 관련이 있기 때문

• 지수함수는 곱을 표현하기 쉽게 함
• log를 쓰면 덧셈으로 바뀌어서 미분과 학습이 쉬워짐

---

Cross entropy

• 분류의 cost function으로 자주 사용

$H(P, Q) = \mathbb{E}_{x \sim P}[-\log Q(x)] = -\sum_{x} P(x) \log Q(x)$

→ $P(x)$: 정답, $Q(x)$: 예측값

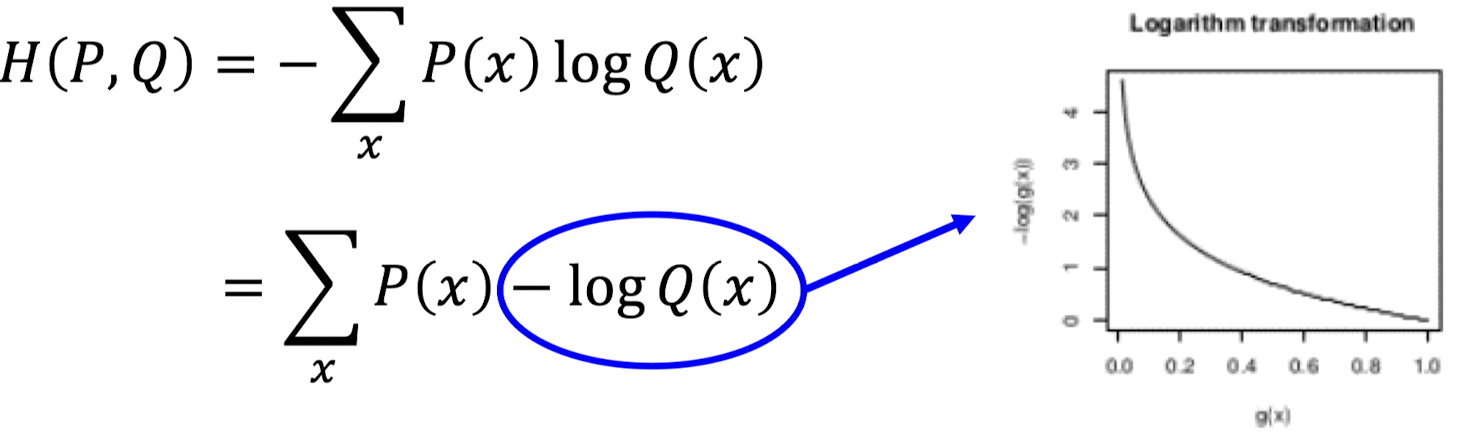
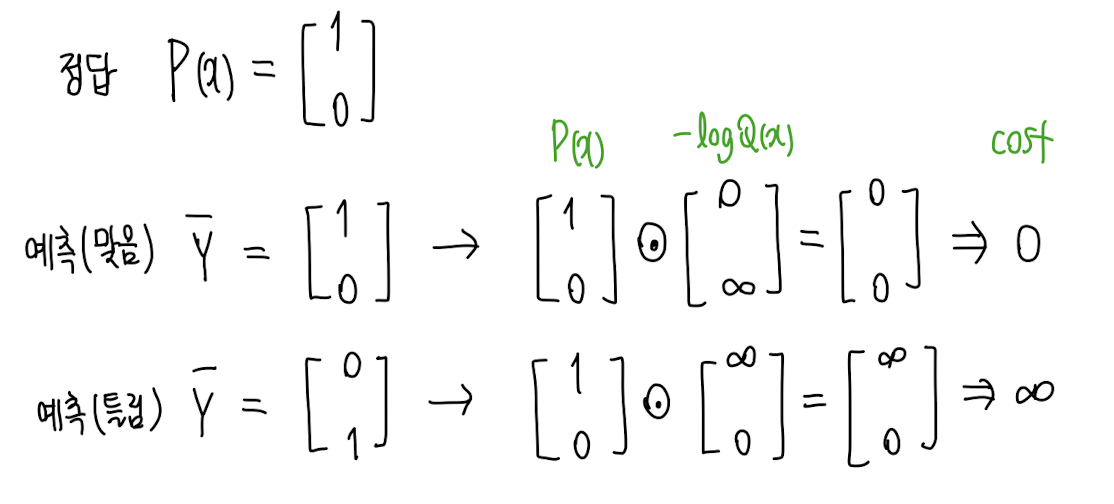
⇒ 0 아니면 1이니까 예측 맞으면 cost 0, 틀리면 무한대

예제

Prediction: $Q(x) = \begin{bmatrix} 0.3075 & 0.4057 & 0.2869 \end{bmatrix}$

Ground truth: $P(x) = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}$

Cross entropy:

$H(P, Q) = -\left(1 \times \log 0.3075 + 0 \times \log 0.4057 + 0 \times \log 0.2869\right)$

---

4.2 Activation functions

활성화 함수가 필요한 이유: 비선형적인 데이터를 분석하기 위해

• 자주 사용되는 활성화 함수 종류

---

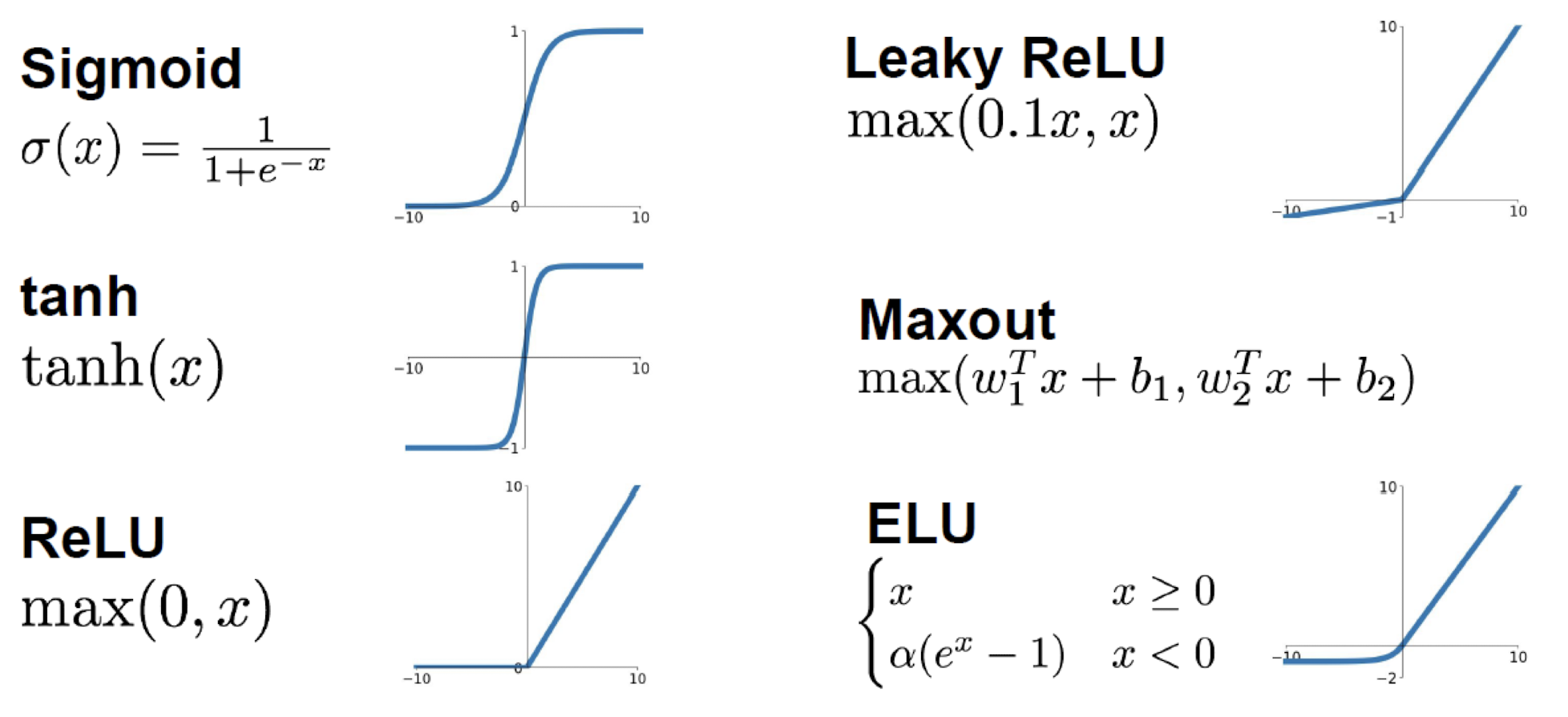
Sigmoid

• 수를 [0, 1]로 매핑시킴
• backpropagation이 0에 가까워져 우리가 찾고자 하는 weight, bias가 사라지는 문제 “Gradient Vanishing”
• sigmoid의 출력값들은 “not zero-centered”
• exp() 연산 비용
  

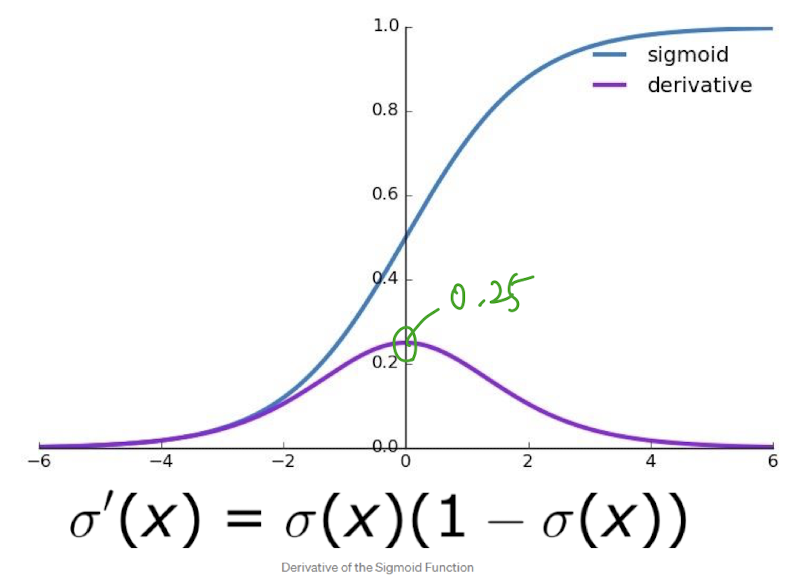
“not zero-centerd”
예측과 정답의 차이가 커도 페널티를 최대 0.25밖에 주지 못함.
다 틀린 경우 0.25 X 0.25 X … 는 0에 수렴하는데, 이는 cost가 0이라는 것
역전파가 진행될수록 아래 layer에 아무 신호가 전달되지 않음

시그모이드 함수의 출력값은 모두 양수기 때문에 경사하강법을 할 때, 그 기울기가 모두 양수거나 음수가 된다. 이로 인해 기울기 업데이트가 지그재그로 변동하고, 학습 속도가 저하된다.

---

tanh

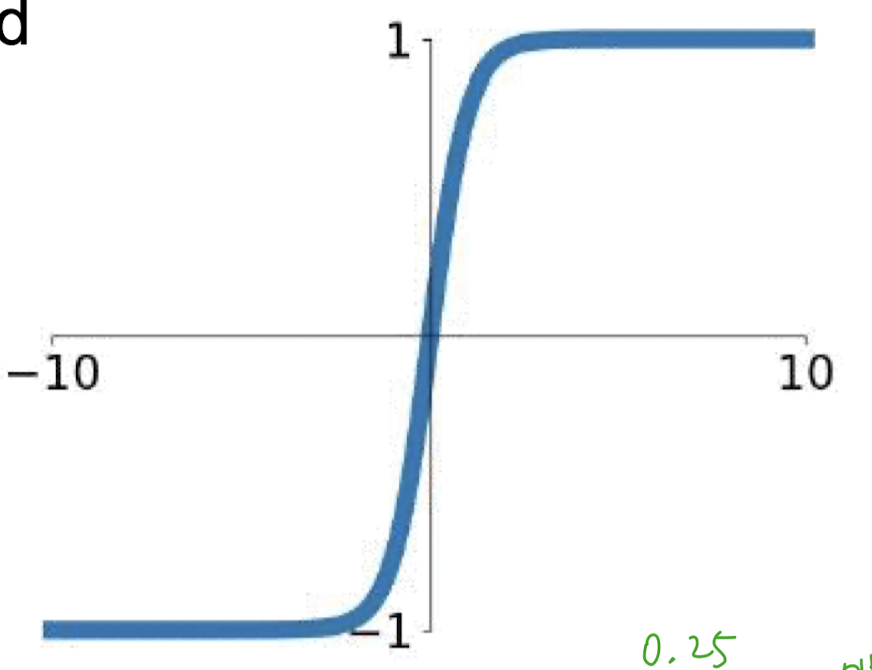
• [-1, 1]
• zero centered
• gradient vanishing

---

ReLU (Rectified Linear Unit)

$f(x)=max(0,x)$

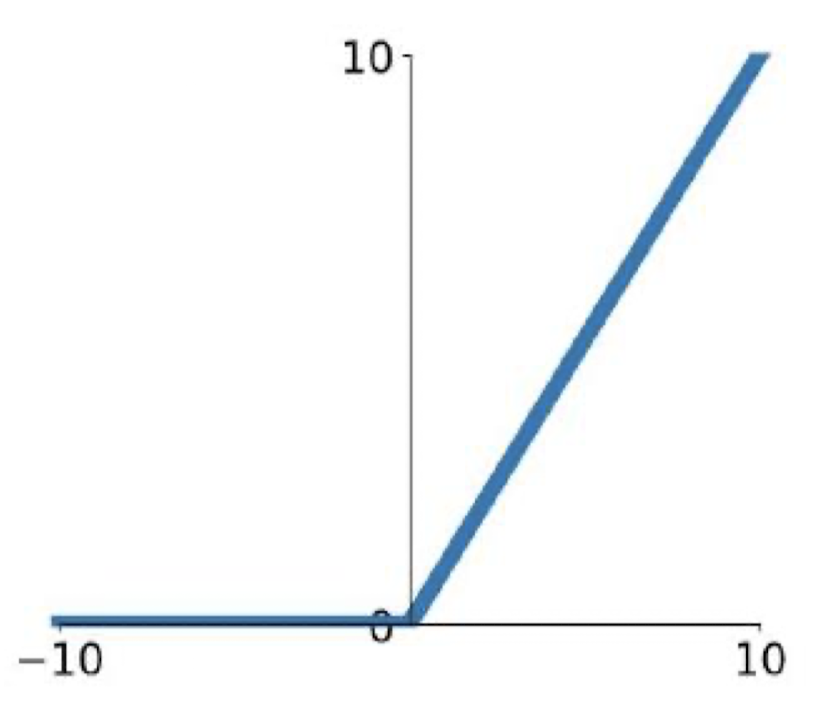
• computationally efficient
• 수렴 속도 빠름

---

Leaky ReLU

$f(x)=max(0.01x, x)$

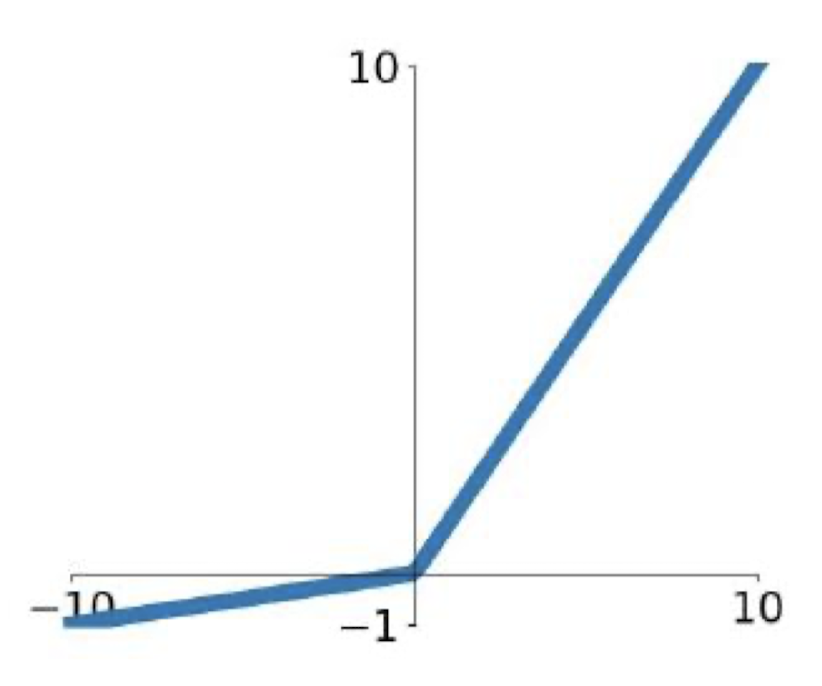
• computationally efficient
• 수렴 속도 빠름
• not “die”