Underfitting / Overfitting

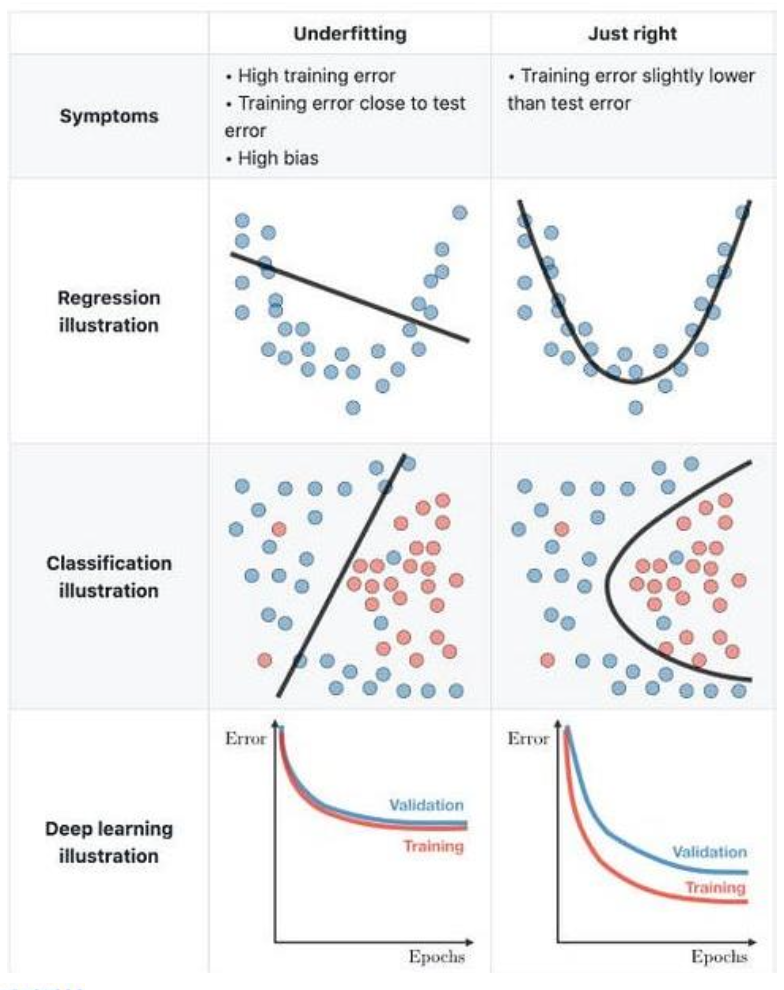
Underfitting

: training과 test error가 모두 높은 것

원인

• 데이터를 나타내기에 모델이 너무 간단함 (모델의 파라미터가 너무 적음)

결과

• 모델이 새로운 데이터를 잘 예측하지 못함 (예측이 편향됨)
• 회귀 계수가 편향됨
• error variance 추정치가 너무 큼

![마지막 그래프에서 train과 val의 에러가 차이나는 이유는! train data의 양이 더 많고, validation은 정답을 보지 않고 하기 때문에 에러가 상대적으로 더 높다.]

마지막 그래프에서 train과 val의 에러가 차이나는 이유는!
train data의 양이 더 많고, validation은 정답을 보지 않고 하기 때문에 에러가 상대적으로 더 높다.

Overfitting

: training error는 낮지만 test error가 높은 것

원인

• 모델이 training data와 관련 없는 특징(노이즈)에 fit
• 모델이 너무 복잡 (모델의 파라미터가 너무 많음)
• training data의 양이 부족

결과

• 모델이 새로운 데이터 예측에 적합하지 않음
• 모델이 너무 복잡해서 노이즈가 새로운 데이터에 대해 같지 않음
• 회귀 계수의 분산이 너무 큼

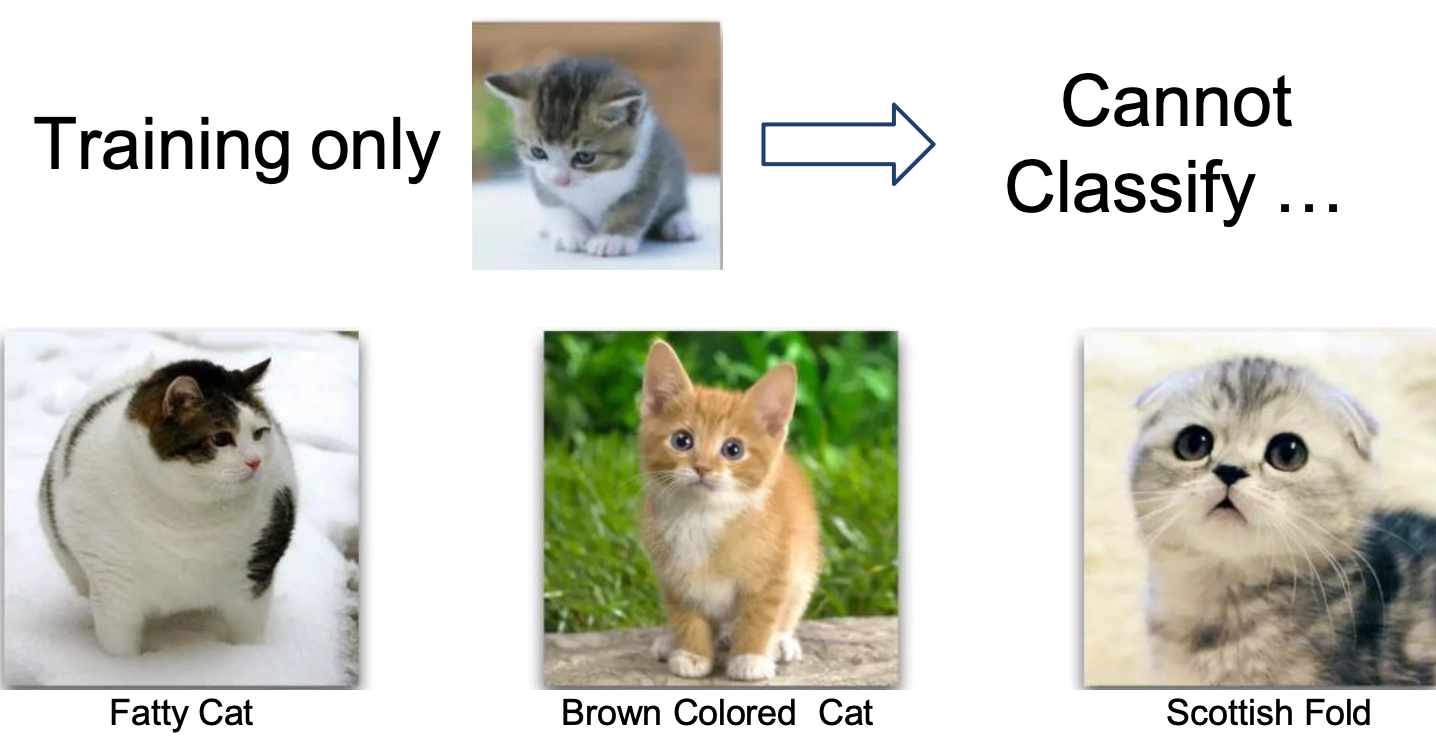
과적합을 간단히 설명하자면 ,

위의 아기고양이와 같은 사진으로만 학습을 해서 아래의 뚱띠고양이(ㅠㅠ), 치즈냥이, 스코티시폴드 등 학습 데이터와 다른 특징을 가진 고양이는 분류하지 못함

---

예측 오차는 두 가지의 구성요소가 있음

→ 모델이 underfitting / overfitting 됐는지 확인하는 방법

Underfitting - low variance, high bias

Overfitting - high variance, low bias

Bias

: 모델이 너무 간단해서 생기는 에러

예측값이 정답과 얼마나 다른지

$\text{Bias}[\hat{f}(x)] = \mathbb{E}[\hat{f}(x)] - f(x)$

Variance

: 훈련 데이터의 무작위성 때문에 생기는 에러 (모델 예측의 변동성)

예측값의 흩어진 정도

$\text{Var}[\hat{f}(x)] = \mathbb{E}\left[(\hat{f}(x) - \mathbb{E}[\hat{f}(x)])^2\right] = \mathbb{E}[\hat{f}(x)^2] - \left(\mathbb{E}[\hat{f}(x)]\right)^2$

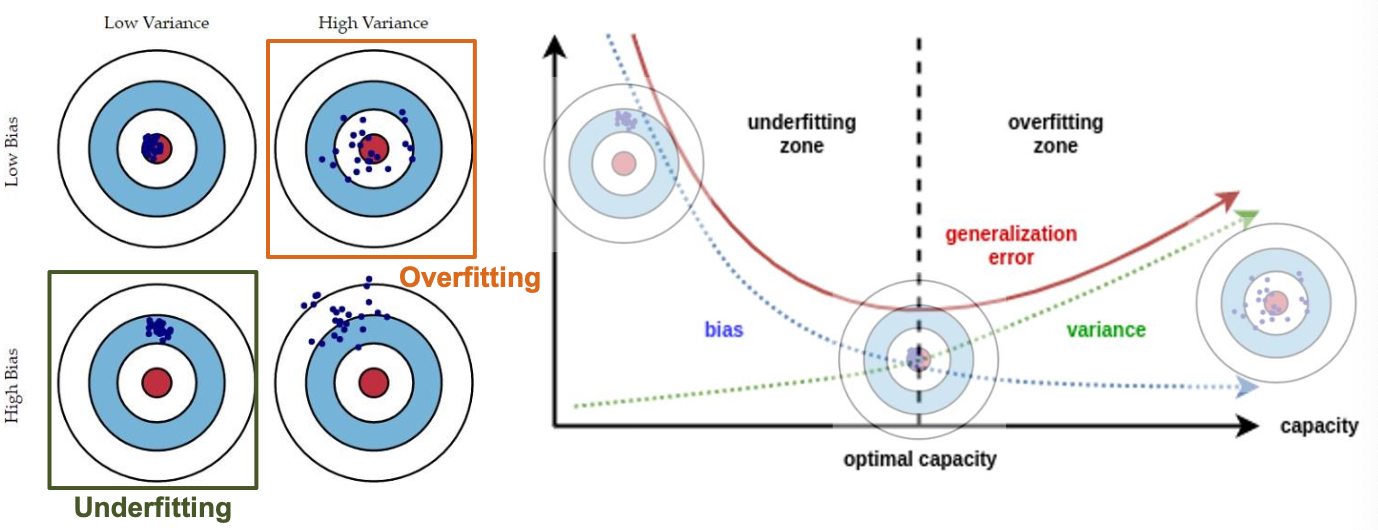
generalization error 일반화 오류: 학습 데이터가 아닌 새로운 데이터에 대해 모델이 예측을 얼마나 잘하는지, 일반화 오류가 작을수록 일반화가 잘 된 모델

Bias-Variance tradeoff

$\text{Error}(x) = \left( \mathbb{E}[\hat{f}(x)] - f(x) \right)^2 + \mathbb{E}\left[ \left( \hat{f}(x) - \mathbb{E}[\hat{f}(x)] \right)^2 \right] + \sigma_\epsilon^2$

Underfitting은 모델을 더 복잡하게 만들면 됨
Overfitting이 더 심각한 문제

---

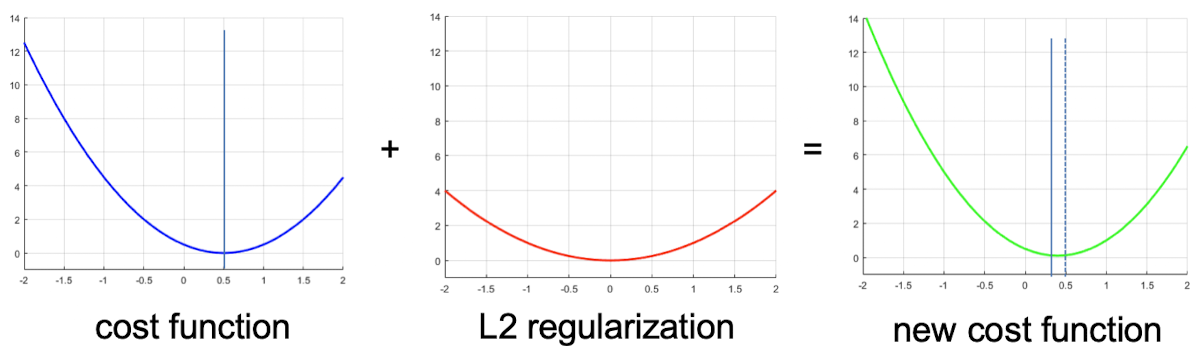
Regularization

: 모델의 복잡성을 제어하여 과적합을 방지하고 일반화 성능을 향상시키는 기법

• 일반화 에러를 줄이기 (training error 아님)

$y=c_1+c_2x+c_3x^2+c_4x^3+c_5x^4+c_6x^5$

$x$ 앞 계수를 0에 가깝도록 낮추면 완만해짐

⇒ “weight, bias 값을 낮추자”가 regularization

$\text{Cost} = \frac{1}{n} \sum_{i=1}^{n} \left\{ L(y_i, \hat{y}_i) + \frac{\lambda}{2} \lVert w \rVert^2 \right\}$ (L2 regularization)

cost function 뒤에 regularization term을 추가

$\lambda$ 값이 커질수록 모델은 간단해짐

---

Dropout

학습마다 랜덤하게 노드를 삭제해서 노드들이 골고루 학습되도록 함

하이퍼파라미터: 노드 삭제율 (0.2 ~ 0.5)

---

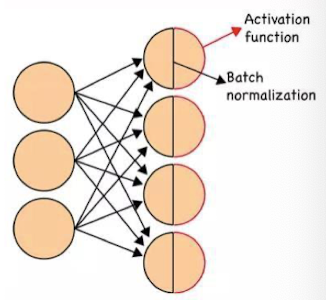
Batch Normalization

입력 데이터셋의 분포는 학습률에 영향을 미침

⇒ 신경망 학습 시 각 층의 입력 분포가 일정하도록 정규화하여 학습을 빠르고 안정적으로 만들기 위한 기술

Normalization

입력 데이터가 같은 분포를 나타내도록 (배치마다 데이터에 차이가 없도록) 정규화, 표준화로 전처리해서 편향되지 않게 함

• min-max normalization: $\hat{x} = \frac{x - \min}{\max - \min}$
• standardization: $\hat{x} = \frac{x - \mu}{\sigma}$

---

covariate Shift

: training, test data에 존재하는 입력 변수의 분포 변화를 의미

Internal covariate shift problem 내부 공변량 변화

데이터 분포가 보이지 않는 요인에 의해 왜곡되는 현상

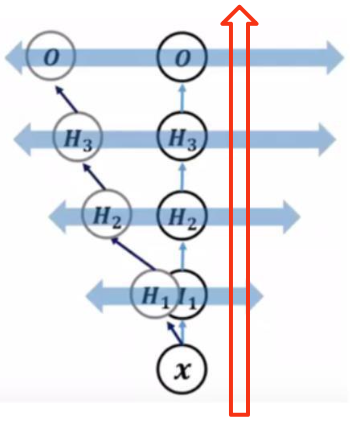
weight의 작은 변화도 가중되어 쌓이면 hidden layer가 깊어질수록 값의 변화도 커짐
⇒ 기존과 다른 값을 갖게 됨

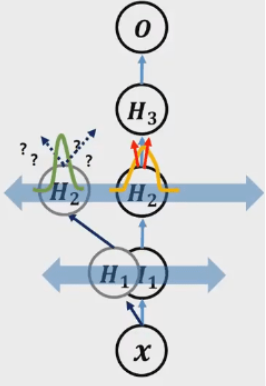
• H2 node까지 변화 없이 안정적으로 같은 값을 가질 때, 이 값을 기준으로 weight 조금씩 바꾸면서 학습하면 잘 됨
• weight 변화 영향으로 H2 node의 값이 바뀌면 기존의 값과 달라져 어떻게 학습해야 할 지 모름

Solution

Whitening: 값들을 정규화 $\hat{x}^k = \frac{x^k - \mathbb{E}[x^k]}{\sqrt{\mathrm{Var}[x^k]}} \qquad {\hat{x} = \frac{x - \mu}{\sigma}}$

→ train, test 데이터를 같은 분포로 변환

• 모든 계층, 단계마다 공분산 행렬 계산해야 됨
• 확률적 알고리즘에서는 bias가 없어지는 문제

---

Batch Normalization

solution for internal covariate shift problem

: 각 미니배치의 모든 계층에서 각 입력 특징의 분포를 N(0, 1)로 정규화

🧑🏻‍🏫 for every mini-batch step

• Step 1 (Whitening): $\hat{x}^k = \frac{x^k - \mathbb{E}[x^k]}{\sqrt{\mathrm{Var}[x^k]}}$
• Step 2: $y^k = \gamma^k \hat{x}^k + \beta^k$
  $\gamma, \beta$는 학습되는 parameter (bias 없어지지 않게 함)

데이터를 표준 가우시안 분포 N(0, 1)로 정규화하면(Step 1) 모델이 표현하려던 비선형성을 제대로 표현할 수 없는 문제가 생김

예) 활성 함수가 시그모이드라면 N(0, 1)로 정규화된 데이터는 시그모이드 함수의 가운데 부분인 선형 영역을 통과하므로 비선형성이 사라짐

따라서 배치 정규화를 하면서 모델의 비선형성을 잘 표현하려면 데이터를 표준 가우시안 분포로 정규화한 뒤 다시 원래 데이터의 분포로 복구해야 함

$\gamma^k$: 표준편차, $\beta^k$: 평균

🧑🏻‍🏫

Batch Normalization Algorithm

입력: 미니배치

$\mathcal{B} = \{x_1, \dots, x_m\}$

학습 파라미터 $\gamma, \beta$

출력:

$y_i = \mathrm{BN}_{\gamma, \beta}(x_i)$

$\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_i$ // 미니배치 평균

$\sigma^2_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_{\mathcal{B}})^2$ // 미니배치 분산

$\hat{x}_i \leftarrow \frac{x_i - \mu_{\mathcal{B}}}{\sqrt{\sigma^2_{\mathcal{B}} + \epsilon}}$ // 표준 정규화

$y_i \leftarrow \gamma \hat{x}_i + \beta \equiv \mathrm{BN}_{\gamma, \beta}(x_i)$ // 원래 분포로 복구

inference(evaluation) 시 BN의 특징

• 입력에 따라 분포가 달라지지 않아야 함
• 전체 training 데이터를 통해 얻은 전역적인 평균과 분산을 사용해야 함
• 결과가 무작위성이 없어야 하며, 고정된 값을 사용해야 함
• 학습 중에는 지수가중평균을 계산하여 전체 데이터 분포를 측정

BN는 활성화함수 이전에 ‼️