https://www.acmicpc.net/problem/7569

문제

철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자모양 상자의 칸에 하나씩 넣은 다음, 상자들을 수직으로 쌓아 올려서 창고에 보관한다.

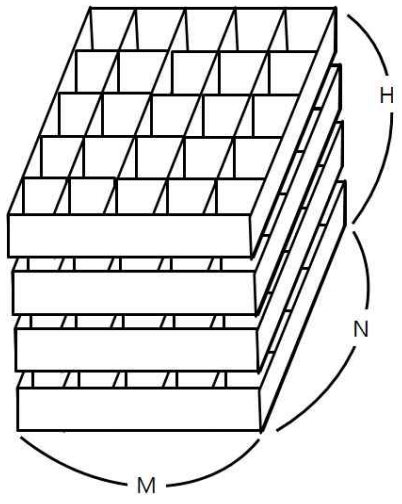
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토에 인접한 곳은 위, 아래, 왼쪽, 오른쪽, 앞, 뒤 여섯 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지 그 최소 일수를 알고 싶어 한다.

토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.

입력

첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100, 1 ≤ H ≤ 100 이다. 둘째 줄부터는 가장 밑의 상자부터 가장 위의 상자까지에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 하나의 상자에 담긴 토마토의 정보가 주어진다. 각 줄에는 상자 가로줄에 들어있는 토마토들의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0 은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다. 이러한 N개의 줄이 H번 반복하여 주어진다.

토마토가 하나 이상 있는 경우만 입력으로 주어진다.

출력

여러분은 토마토가 모두 익을 때까지 최소 며칠이 걸리는지를 계산해서 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.

풀이

먼저 문제를 보니 배열 느낌이 와서 3차원 배열을 만들어 줬다.
여기서 주의할 점은 3차원 구조를 생각할 때 우리는 흔히 (x, y, z)처럼 가로 세로 높이 순으로 쓰지만, 컴퓨터는 배열 안에 배열을 저장하는 것이기 때문에 (z, y, x)순으로 구현해주어야 한다. 2차원 배열에서 행을 먼저 정하고 열을 나중에 정하듯이.

int[][][] tomato = new int[h][n][m];

그 다음 배열에 토마토를 넣...기 전에, 익은 토마토가 얼마나 퍼지는지 알기 위해서 익은 토마토들의 위치 정보가 필요하다. 익은 토마토를 기준으로 주변 토마토들이 익으므로 탐색의 시작점이 되는 위치를 저장해 두어야 하는 것이다. 그래서 따로 위치 정보를 저장할 수 있도록 Location이라는 클래스를 만들어 주었다.

class Location {
	int z;
	int y;
	int x;

	Location(int z, int y, int x) {
		this.z = z;
		this.y = y;
		this.x = x;
	}
}

익은 토마토의 위치 정보를 저장하는 큐를 만들어서 위치를 저장한다.
덤으로 덜 익은 토마토의 개수도 미리 세 주었다.

for (int i = 0; i < h; i++)
		for (int j = 0; j < n; j++)
			for (int k = 0; k < m; k++) {
				tomato[i][j][k] = sc.nextInt();
				if (tomato[i][j][k] == 0)
					greenTomato++;
				else if (tomato[i][j][k] == 1)
					redTomato.add(new Location(i, j, k));
			}

 

이제 이미 다 익었는지/얼마만에 익는지/다 익지 못하는지만 알아내면 된다!
이미 다 익었는지를 알아내는 것은 간단하다. 덜 익은 토마토가 없으면 이미 익은 토마토밖에 없다는 뜻이니까.
그렇다면 얼마만에 익는지/다 익지 못하는지만 알아내면 되는데, 이건 앞서 저장한 익은 토마토의 위치 정보를 기준으로 하나하나 토마토를 익히는 수밖에 없다.

좋아, 그렇다면 이제 토마토를 익혀보자! 그런데 어떻게 익히지?
문제에서 주어진 대로 익은 토마토는 주변 6방향의 덜 익은 토마토를 익게 하니까 그걸 구현하면 될 것 같은데... 그렇지만 하나하나 판단하기에는 아무리 생각해도 너무 코드가 복잡해지는 것 같고.

그래서 다른 사람들의 코드를 참고한 결과 아예 주변 6방향의 좌표 변화량을 배열에 넣어두고 그 값을 더하는 방식을 썼다. 양옆은 x좌표만, 앞뒤는 y좌표만, 위아래는 z좌표만 변하니까... 이런 식으로.

int[] rz = { 0, 0, 0, 0, -1, 1 };
int[] ry = { 0, 0, -1, 1, 0, 0 };
int[] rx = { -1, 1, 0, 0, 0, 0 };

즉 하나의 익은 토마토에 대해 주변 6방향을 모두 검사하고 다음으로 넘어가는 방식이다. 이렇게 하면 예외처리 구문도 한꺼번에 모아서 continue로 넘겨버릴 수 있으니 더 간편하다(라고 생각한다...).

for (int j = 0; j < 6; j++) {
	int nz = z + rz[j];
	int ny = y + ry[j];
	int nx = x + rx[j];

	//범위에 맞지 않으면
	if (nz < 0 || ny < 0 || nx < 0 || nz >= h || ny >= n || nx >= m)
		continue;
    //덜 익은 토마토가 아니면
	else if (tomato[nz][ny][nx] != 0)
		continue;
        
    ...
}

이제 덜 익은 토마토를 익게 하고, 새롭게 익은 토마토의 위치를 큐에 저장한다.

greenTomato--; //덜 익은 토마토 개수 감소
tomato[nz][ny][nx] = 1; //해당 위치의 토마토를 익은 토마토로 변경
redTomato.add(new Location(nz, ny, nx));

 

이 과정을 처음에 있었던 익은 토마토의 개수만큼 반복한다. 반복이 끝나면 하루가 지난 것이므로 일수를 증가시키고 남아있는 익은 토마토에 대해 다시 반복을 시작한다.

int size = redTomato.size();
for(int i = 0; i < size; i++){
	//위의 연산
}
days++;

 

위의 모든 과정을 덜 익은 토마토가 없어지거나 새롭게 익은 토마토가 없을 때까지 반복한다.

while (greenTomato > 0 && !redTomato.isEmpty()){
	//위의 과정
}

 

알고리즘이 모두 끝나면 덜 익은 토마토가 남아 있는지 확인한다.
덜 익은 토마토가 남아 있다면->다 익지 못한 것이므로 -1을 출력한다.
덜 익은 토마토가 없다면->다 익은 것이므로 걸린 일수를 출력한다.

System.out.println(greenTomato == 0 ? days : -1);

전체 코드

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

class Location {
	int z;
	int y;
	int x;

	Location(int z, int y, int x) {
		this.z = z;
		this.y = y;
		this.x = x;
	}
}

public class BJ_7569 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int[] rz = { 0, 0, 0, 0, -1, 1 };
		int[] ry = { 0, 0, -1, 1, 0, 0 };
		int[] rx = { -1, 1, 0, 0, 0, 0 };

		int m = sc.nextInt();
		int n = sc.nextInt();
		int h = sc.nextInt();

		int[][][] tomato = new int[h][n][m];
		Queue<Location> redTomato = new LinkedList<>();
		int greenTomato = 0, days = 0;

		for (int i = 0; i < h; i++)
			for (int j = 0; j < n; j++)
				for (int k = 0; k < m; k++) {
					tomato[i][j][k] = sc.nextInt();
					if (tomato[i][j][k] == 0)
						greenTomato++;
					else if (tomato[i][j][k] == 1)
						redTomato.add(new Location(i, j, k));
				}

		while (greenTomato > 0 && !redTomato.isEmpty()) {
			int size = redTomato.size();
			for(int i = 0; i < size; i++){
				Location l = redTomato.remove();
				int z = l.z;
				int y = l.y;
				int x = l.x;

				for (int j = 0; j < 6; j++) {
					int nz = z + rz[j];
					int ny = y + ry[j];
					int nx = x + rx[j];

					if (nz < 0 || ny < 0 || nx < 0 || nz >= h || ny >= n || nx >= m)
						continue;
					else if (tomato[nz][ny][nx] != 0)
						continue;

					greenTomato--;
					tomato[nz][ny][nx] = 1;
					redTomato.add(new Location(nz, ny, nx));
				}
			}
			days++;
		}
        
		System.out.println(greenTomato == 0 ? days : -1);
	}
}

 

+

진짜 정말로 어마어마하게 삽질한 문제. 처음에 DFS로 고민하다 왜안되지? 했는데 BFS로 하는 거였고...^^ 밑에 분류 좀 보자 제발
(사실 BFS인 걸 알고도 한참을 고민하다 결국 검색해가며 겨우겨우 풀었다)

개인적으로 일수를 계산하는 부분이 너무 어려웠다. 그냥 다 익는지 여부만 판단하는 거라면 탐색 알고리즘을 그냥 쓰기만 하면 되는데, 다 익는데 얼마나 걸리는지를 계산해야 하다 보니 많이 헤맸다. 그리고 인접한 정점을 찾아내는 것도. 아니 사실 그냥 전부 다...

이렇게 정리해도 사실 완전히 이해했다는 느낌은 안드는데, 그래도 일단 넘어가야겠다. 너무 한 문제만 붙잡고 있는 것도 좋은 건 아니고.

그리고 적당히 고민하고 그냥 찾아보거나 물어보자! 혼자 잡고 있지 말고! 막히는 부분이 생기면 한 2~3시간 정도만 고민하다가 그냥 찾아보자!!!

BFS는 DFS랑 달리 큐에 넣고 방문했다고 표시한다는 점에서 좀 더 직관적인 것 같다. DFS는 스택에 넣고 뺄 때가 되어서야 방문했다고 표시하니까.