[백준 11404번] 플로이드

mokomoko·2022년 1월 17일

python 백준

1. 문제

n(2 ≤ n ≤ 100)개의 도시가 있다.
그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1 ≤ m ≤ 100,000)개의 버스가 있다.
각 버스는 한 번 사용할 때 필요한 비용이 있다.

모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.

제한 사항

시간 : 1 초
메모리 : 256 MB

입력

첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.

시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.

출력

n개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다. 만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.

- 키워드

플로이드 마샬 알고리즘을 사용하자.

2. 풀이

플로이드를 풀기 전에 이전에 배웠던 다익스트라로 구현을 해봤다.

정답은 나왔으나 플로이드로 풀었을 때보다 긴 시간을 소모하게 되었다.

해당 문제의 이름은 플로이드이므로, 플로이드에 대해서 알아보았다.

먼저 다익스트라와 플로이드의 차이는 다음과 같다.

다익스트라 알고리즘은 "특정 노드"에서 도착 지점까지 최단 경로를 구하기 용이
플로이드 알고리즘은 "모든 노드"에서 "모든 노드"까지 최단 경로를 구하기 용이

즉, 해당 문제와 같이 모든 노드의 각각의 최단 경로를 구하기 위해서는

플로이드 알고리즘을 사용해야 한다.

원리는 간단한 편이다.

해당 테스트 케이스를 살펴보자.

5
14
1 2 2
1 3 3
1 4 1
1 5 10
2 4 2
3 4 1
3 5 1
4 5 3
3 5 10
3 1 8
1 4 2
5 1 7
3 4 2
5 2 4

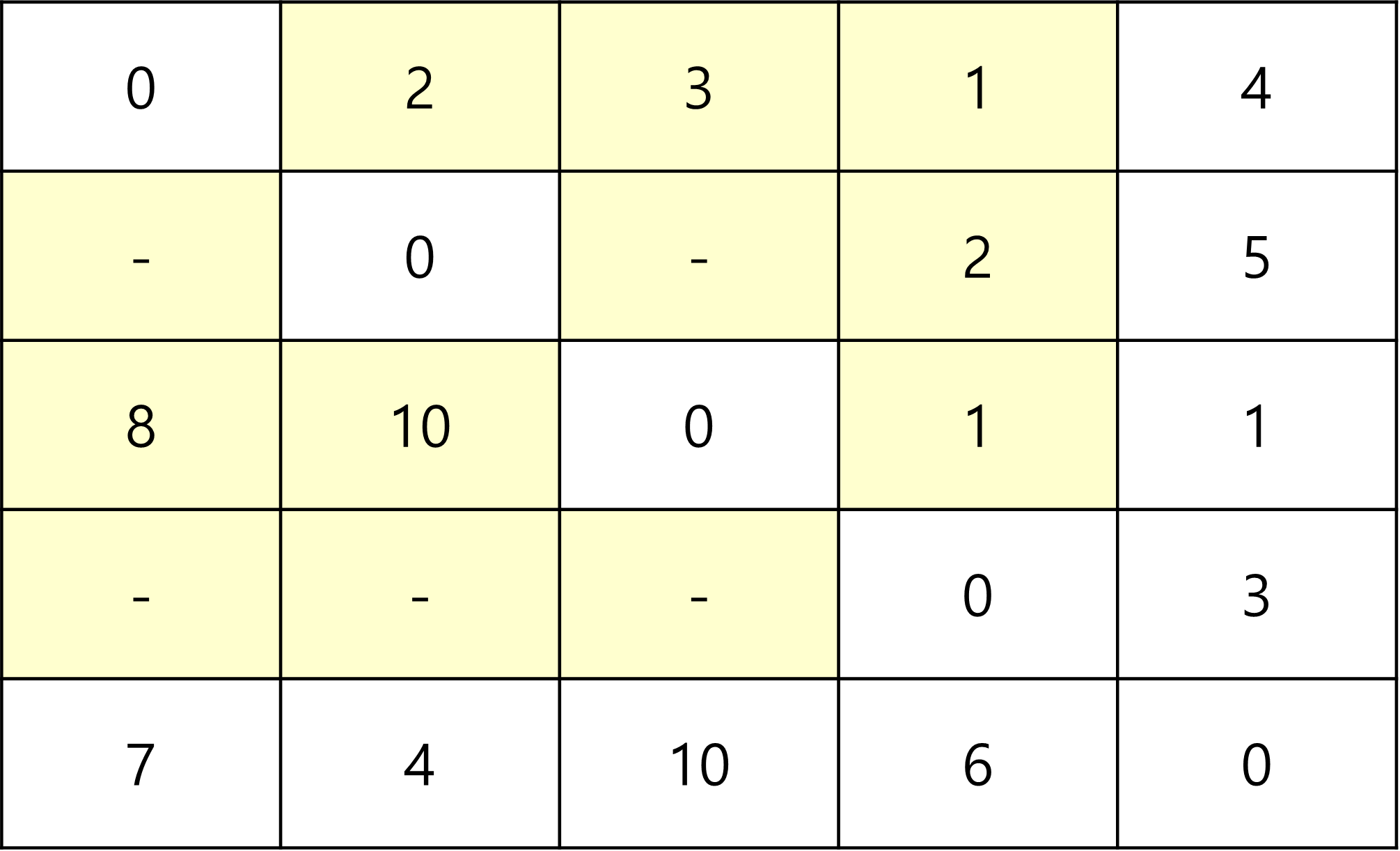
해당 테스트케이스를 그래프화 시키면 다음과 같다.

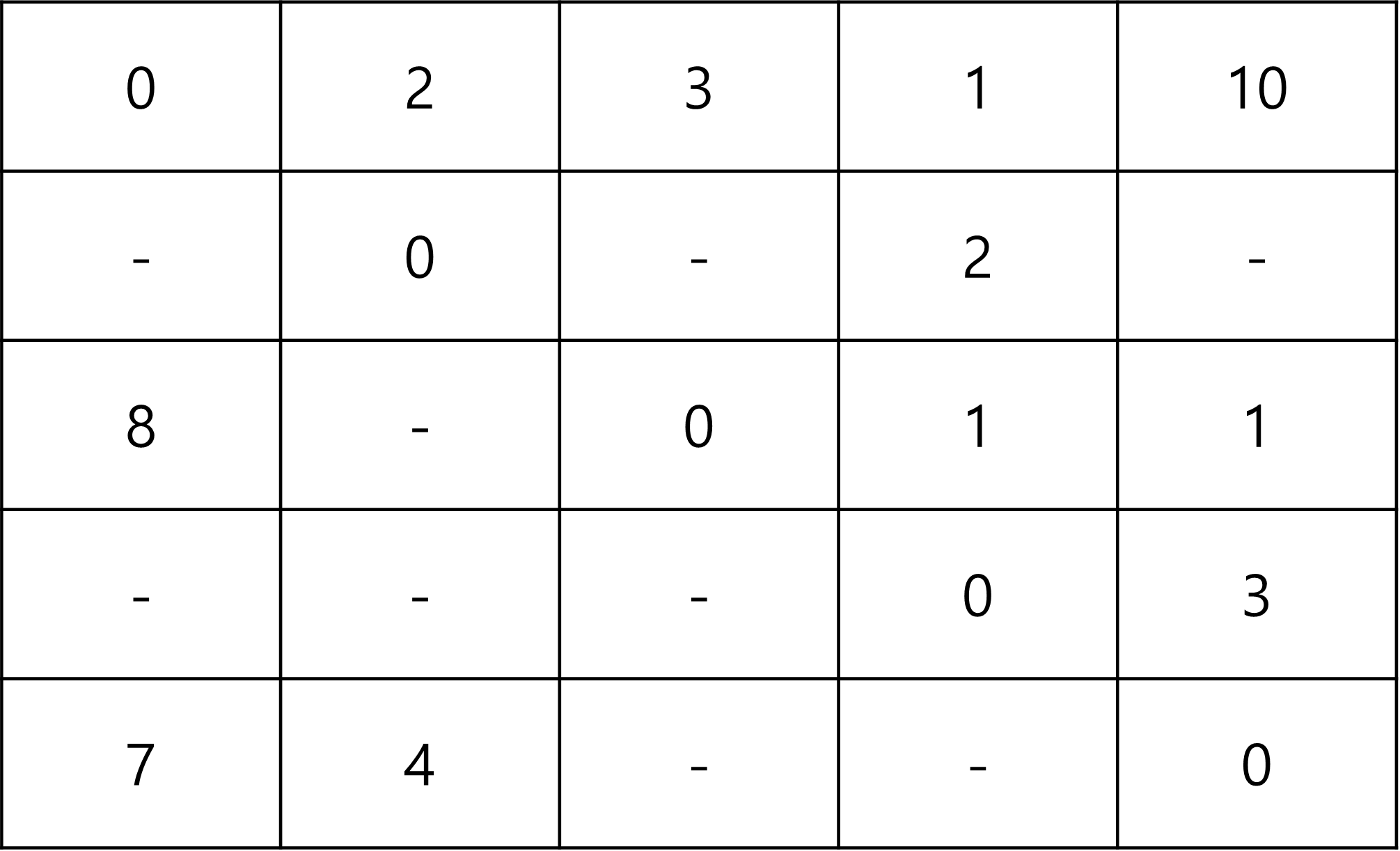
여기서 '-' 는 아직 경로를 모르는상태며, INF로 지정해주었다.

먼저, 중간 지점으로 1을 통과해서 가는 경우의 수를 갱신한다.

그러므로 1이 출발 지점이나 도착지점이 아닌 부분이 수정된다.

해당 부분이 수정되는데, 원리는 다음과 같다.

기존 저장되어 있는 "출발 -> 도착" 보다 "출발 -> 중간 + 중간 -> 도착" 이 더 빠른가?를 기준으로

채워넣는다.

그러므로, 위의 예제에서 갱신을 하게되면, 다음과 같이 갱신이 된다.

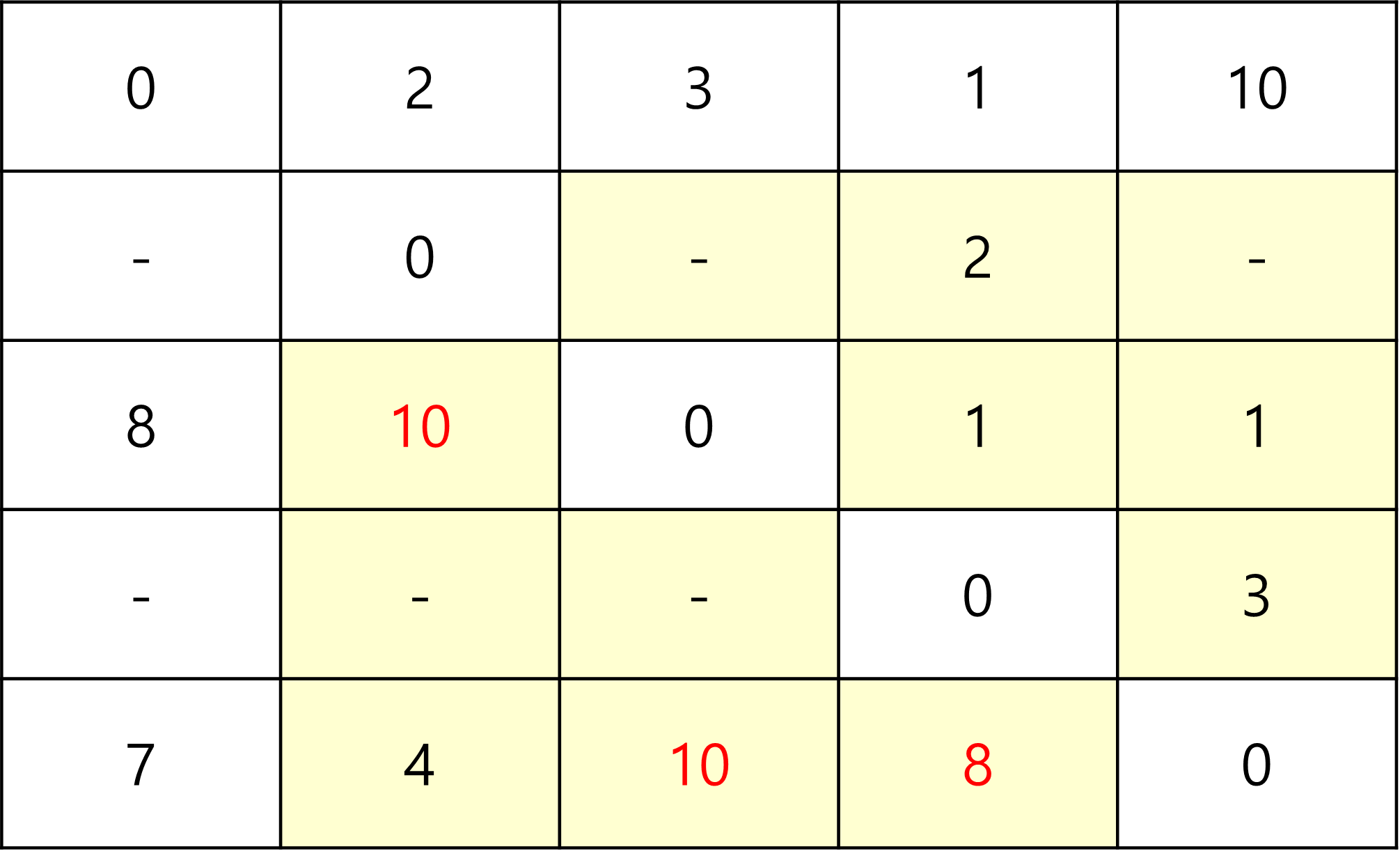
1을 중간 지점으로 지정해서 갈 수 있는 곳은 3,5뿐이며,

3 -> 1 + 1 -> 2 ,
5 -> 1 + 1 -> 3 ,
5 -> 1 + 1 -> 4

3가지 경로가 기존 경로값보다 작으므로 갱신된다.

다음은 2를 중간 지점으로 통과해서 가는 경우의 수다.

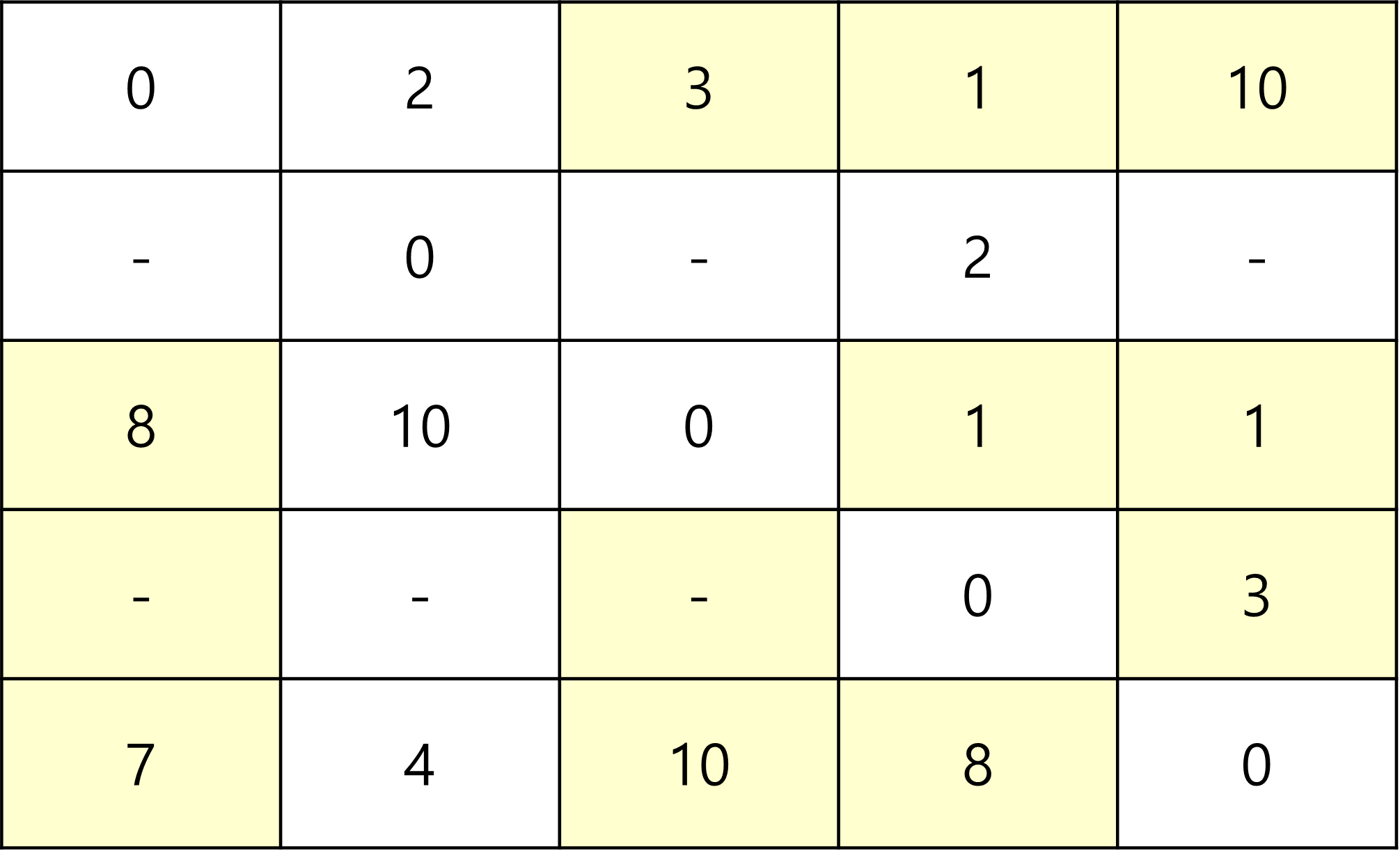
2를 중간 지점으로 해서 통과하는 부분은 다음과 같고 똑같이

2를 중간 지점으로 지나갈 수 있는 곳 중 더 짧은 경로가 있다면 갱신된다

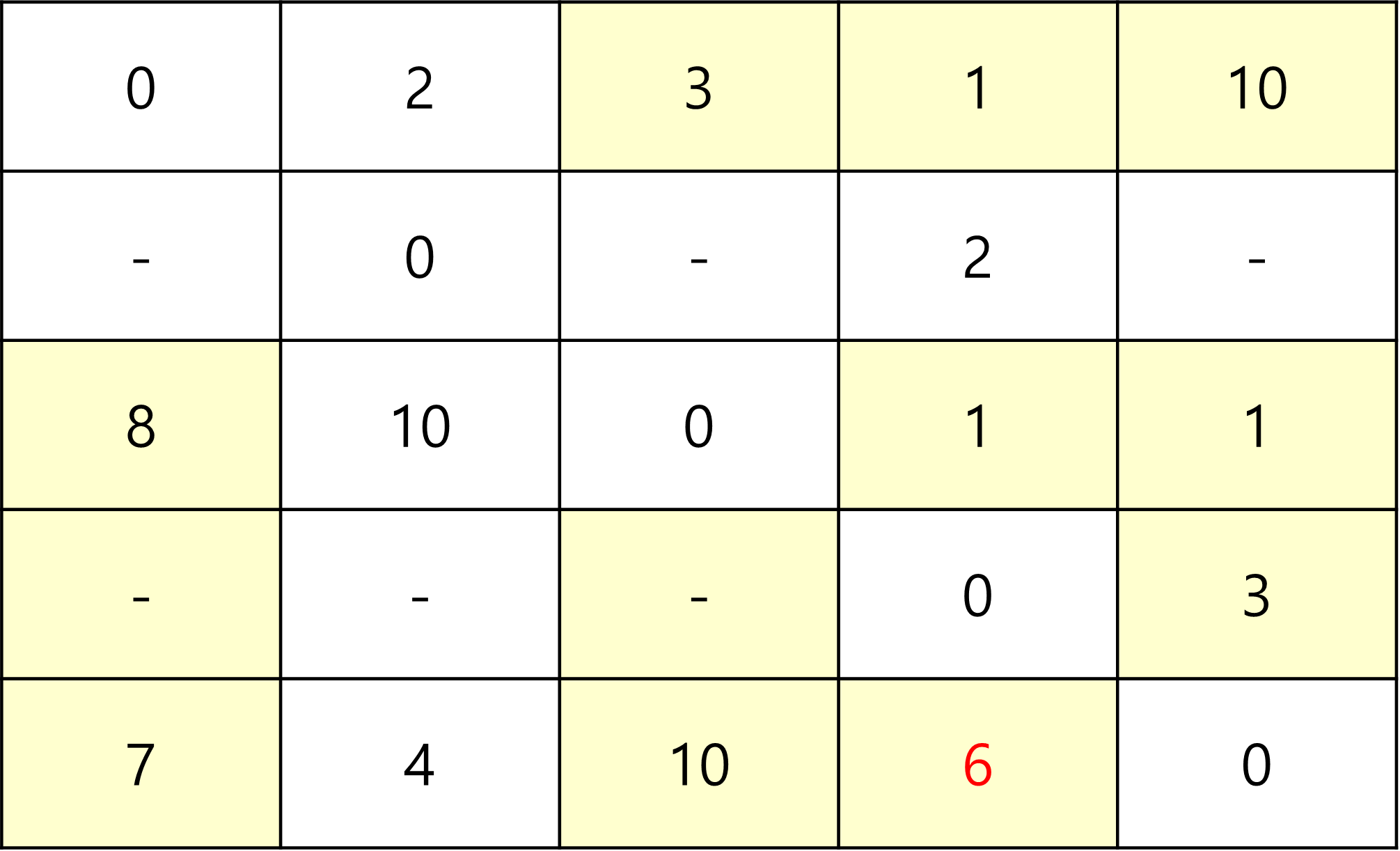
기존 8보다 5 -> 2(4) + 2 -> 4(2) 가 더 짧으므로 갱신

그리고 3을 중간 지점으로 통과하는 부분이다.

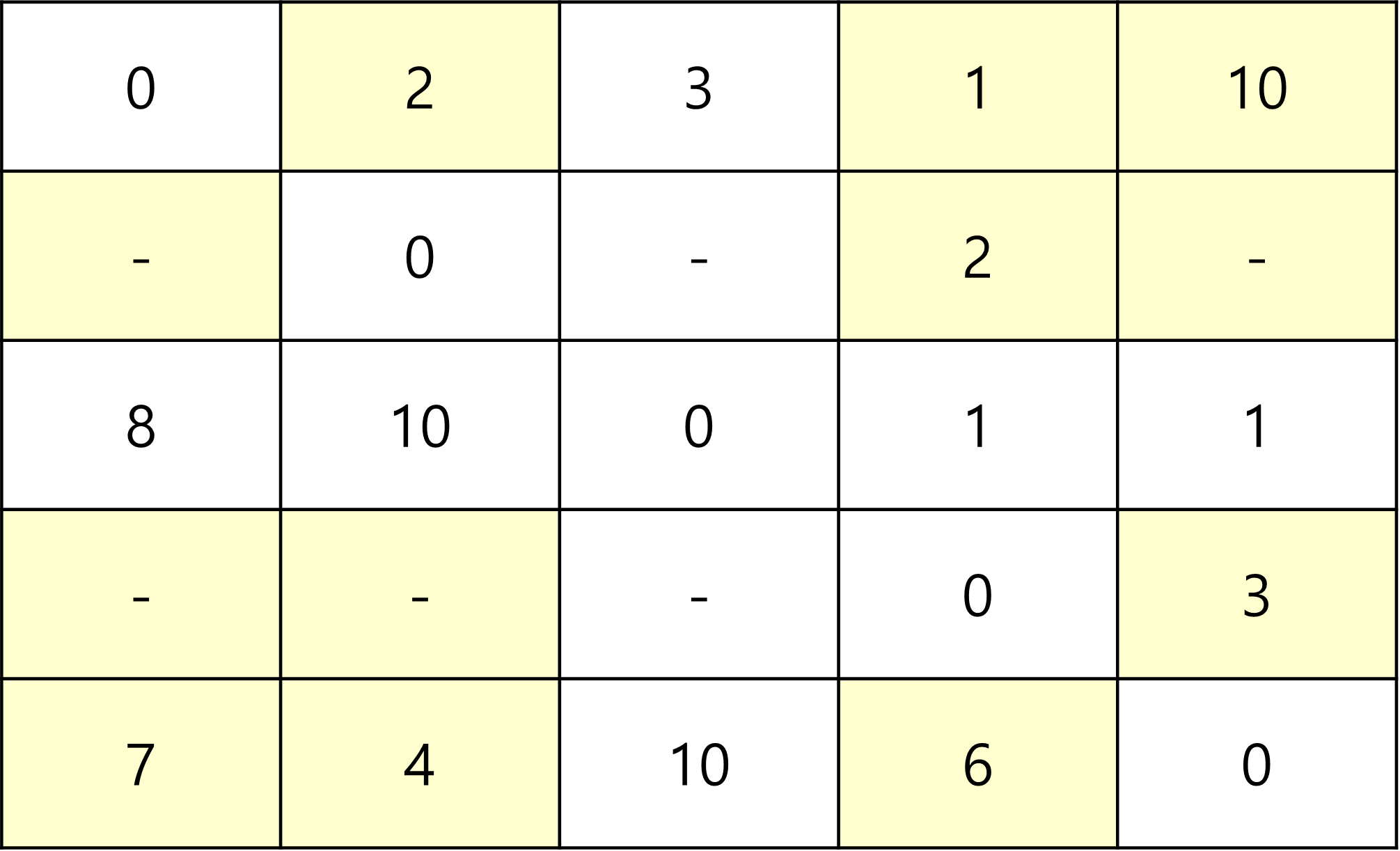
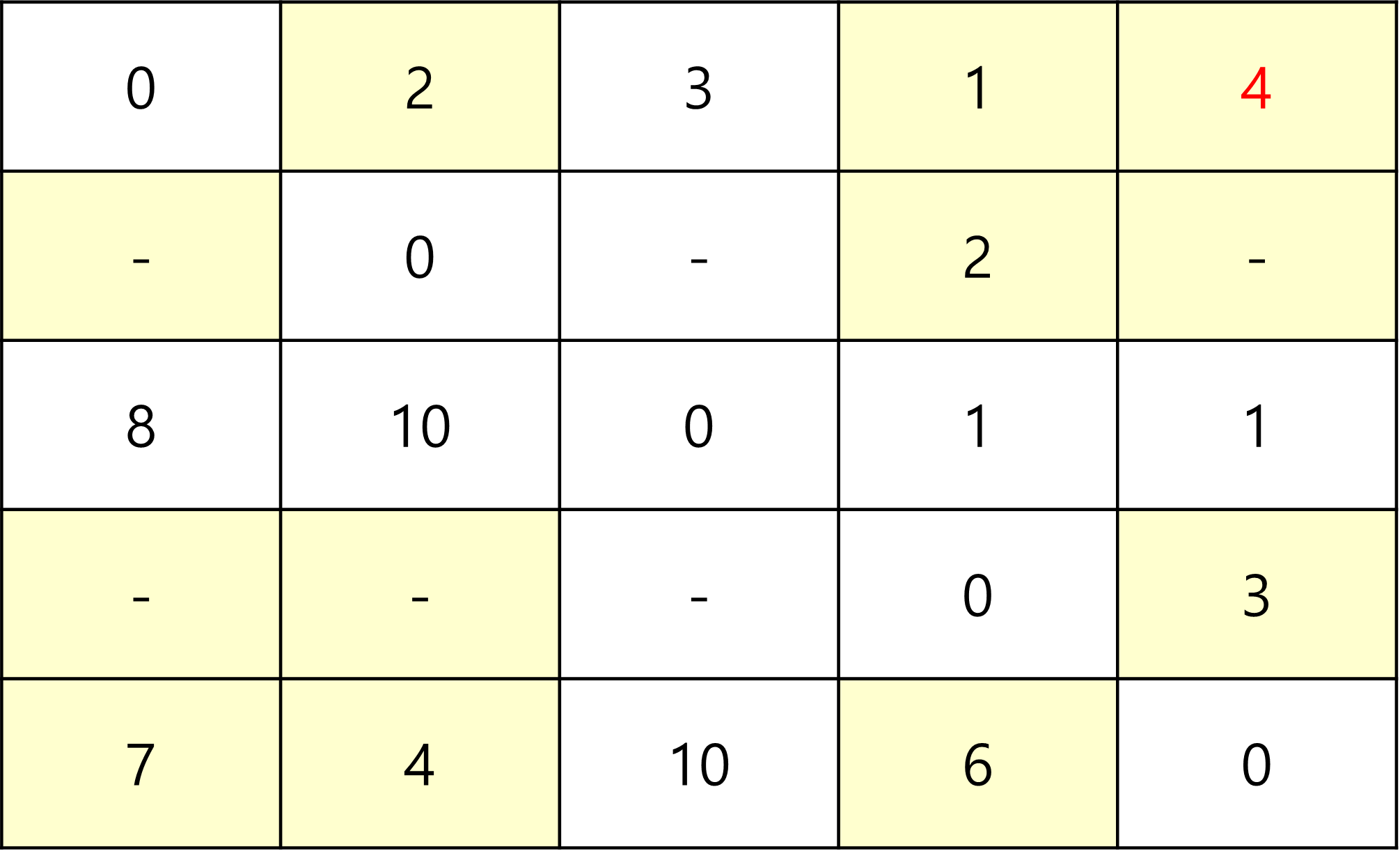
3을 중간 지점으로 갈 수 있는 곳은 1,5뿐이고,

10보다 1 -> 3(3) + 3 -> 5(1)가 더 짧으므로 갱신

다음은 4를 중간 지점으로 통과하는 부분이다.

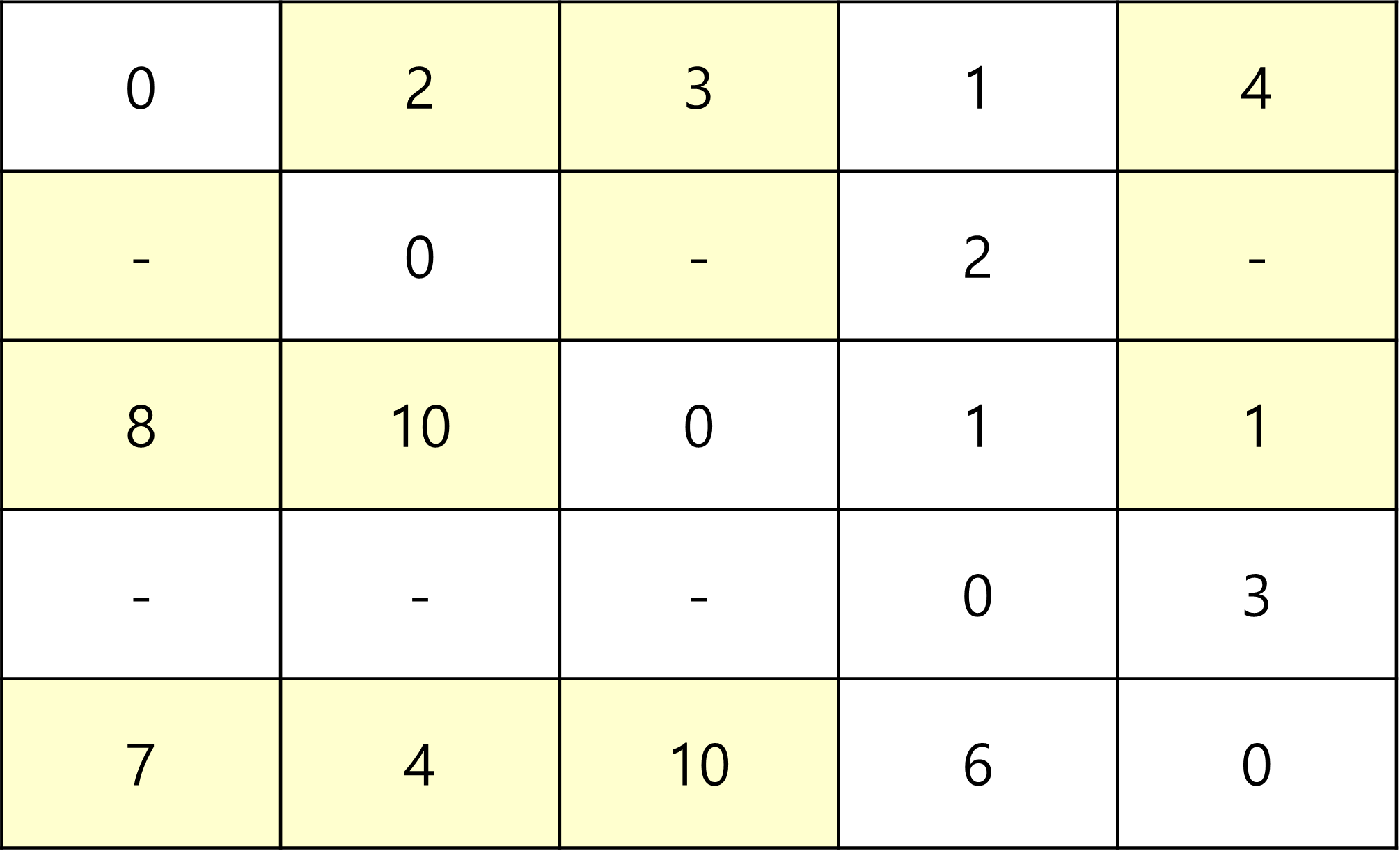
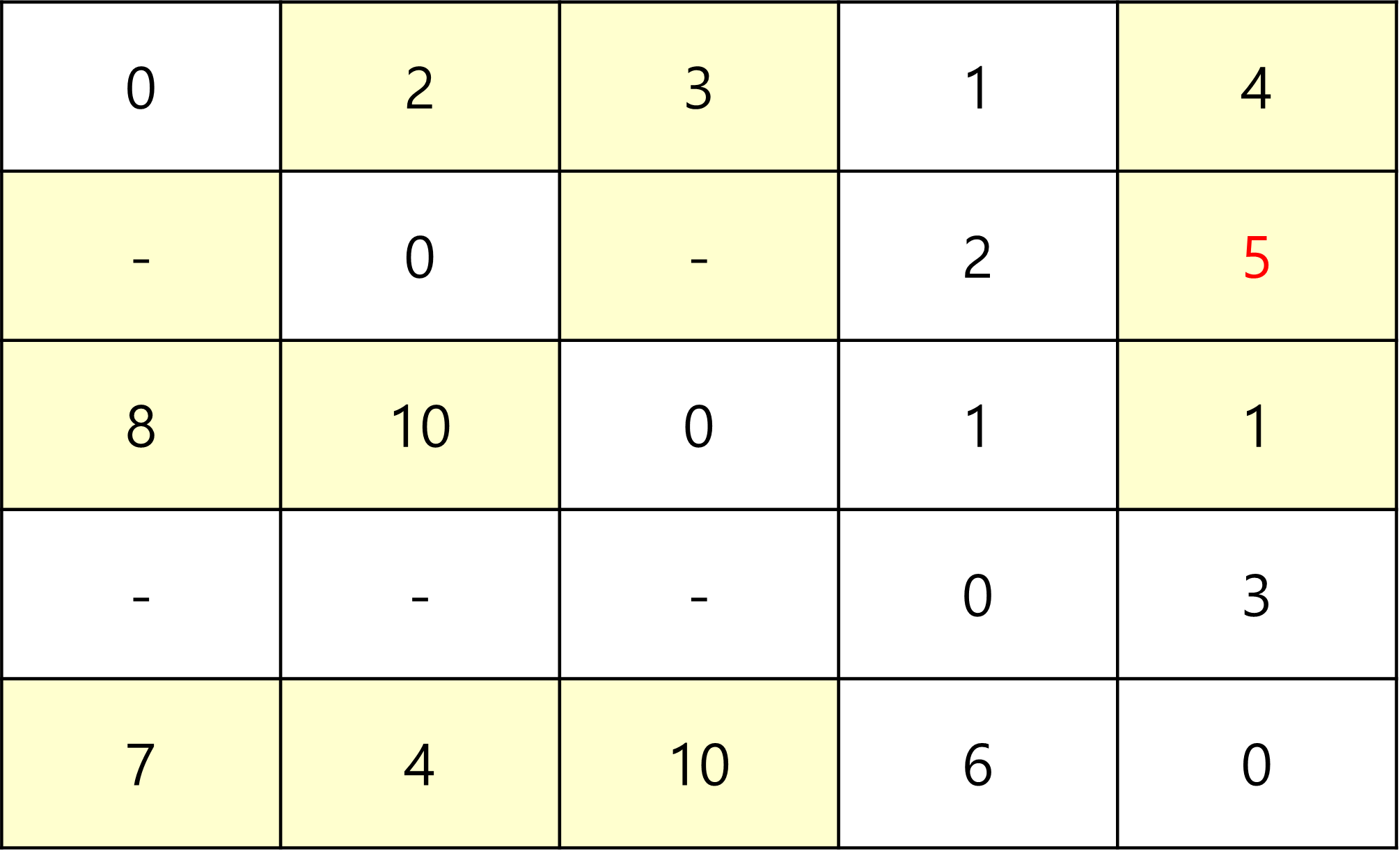
2->4(2) + 4->5(3) 이 INF보다 짧으므로 갱신

마지막으로 5를 중간 지점으로 통과하는 부분이다.

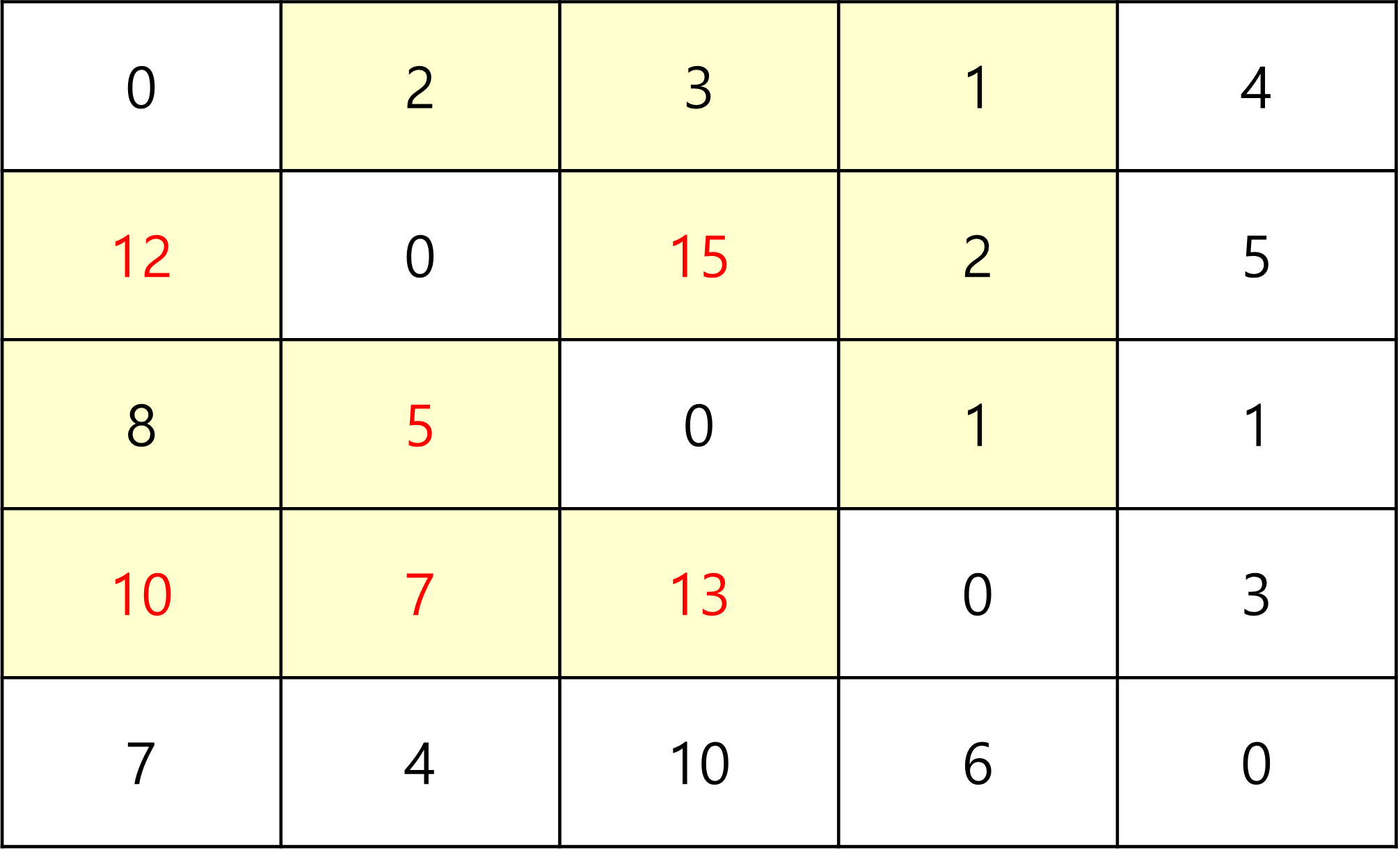
2 -> 5 + 5 -> 1
2 -> 5 + 5 -> 3
3 -> 5 + 5 -> 2
4 -> 5 + 5 -> 1
4 -> 5 + 5 -> 2
4 -> 5 + 5 -> 3

총 6개의 최단 경로가 갱신 되었다.

그렇게 해서 결과는 다음과 같이 나온다.

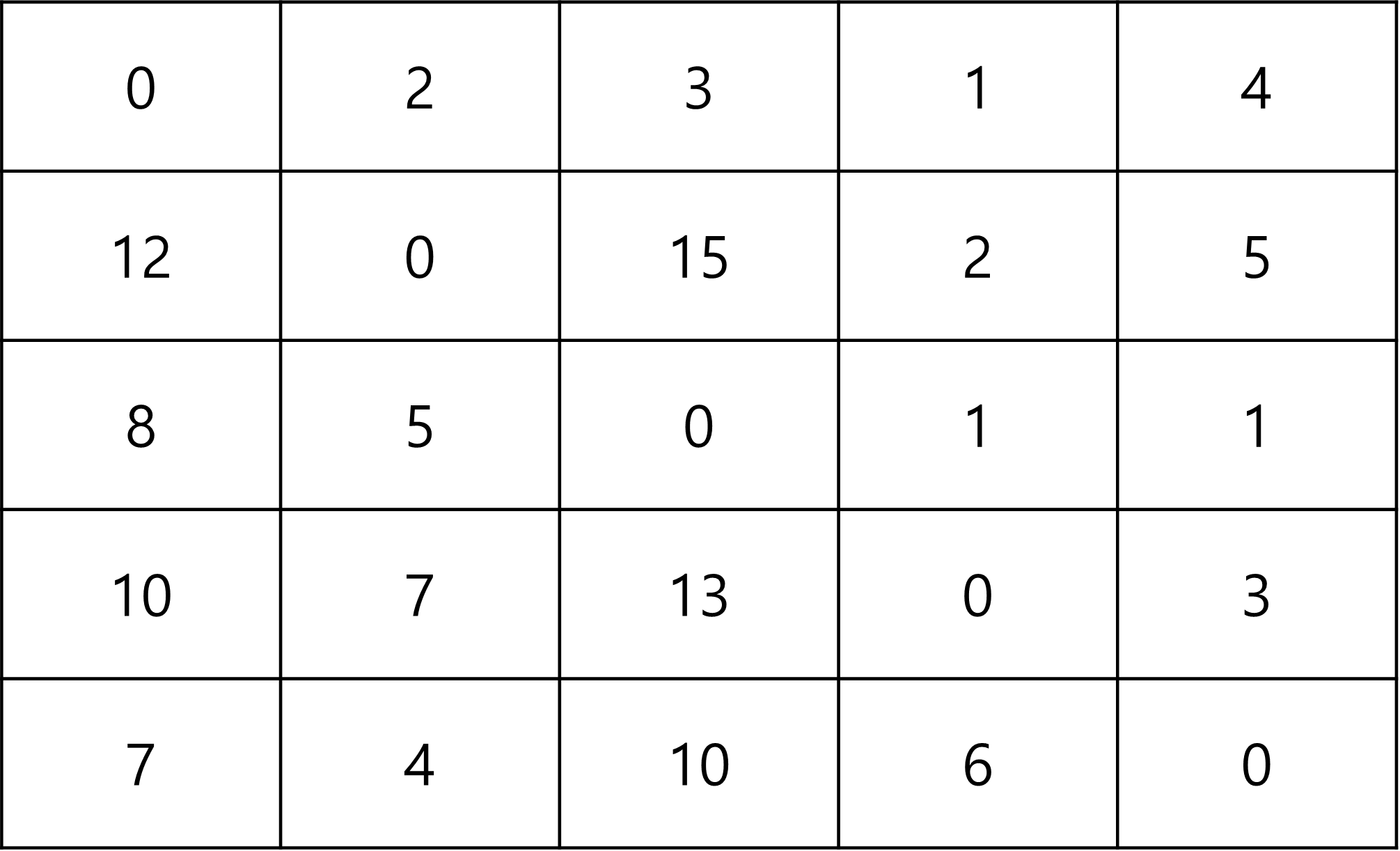
3. 소스코드

import sys
# import heapq
input = sys.stdin.readline
INF = float('inf')
# dijkstra
# def search(start,bus,N):
# 	q = []
# 	result = [INF] * (N+1) 
# 	heapq.heappush(q,[0,start])
# 	while q:
# 		cost,now = heapq.heappop(q)
# 		for edge in bus[now]:
# 			end,c = edge
# 			if result[end] > cost + c:
# 				result[end] = cost+c
# 				heapq.heappush(q,[cost+c,end])
# 	result[start] = 0
# 	for i in range(1,N+1):
# 		if result[i] == INF:
# 			result[i] = 0 
# 	return result

# def solution(bus,N,M):
# 	answer = []
# 	for i in range(1,N+1):
# 		answer.append(search(i,bus,N))
# 	for i in answer:
# 		for j in range(1,N+1):
# 			print(i[j],end=" ")
# 		print()
# floyd
def solution(bus,N,M):
	for i in range(1,N+1):
		bus[i][i] = 0
	for mid in range(1,N+1):
		for start in range(1,N+1):
			for end in range(1,N+1):
				bus[start][end] = min(bus[start][end],bus[start][mid]+bus[mid][end])
	for i in range(1,N+1):
		for j in range(1,N+1):
			if bus[i][j] != INF:
				print(bus[i][j],end=" ")
			else:
				print(0,end=" ")
		print()


if __name__ == "__main__":
	N = int(input())
	M = int(input())
	# bus = dict()
	# for i in range(1,N+1):
	# 	bus[i] = []
	# for _ in range(M):
	# 	start,end,cost = map(int,input().split())
	# 	bus[start].append([end,cost])
	bus = [[INF] * (N+1) for _ in range(N+1)]
	for _ in range(M):
		start,end,cost = map(int,input().split())
		bus[start][end] = min(cost,bus[start][end])
	
	solution(bus,N,M)