1. 문제
트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.
제한 사항
시간 : 1 초
메모리 : 256 MB
입력
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.
먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.
출력
첫째 줄에 트리의 지름을 출력한다.
- 키워드
- BFS를 이용하여 가장 먼 정점을 찾아낸다.
2. 풀이
해당 문제를 풀때 여러 생각을 해봤다.
BFS는 맞는데 시작지점이 어딘지 모르기 때문에,
이것을 탐색을 할 때 중간중간 기록을 해야하나..
기록한 걸 토대로 가장 먼 거리를 계산할 수 있지 않을까? 싶었는데...
1시간정도 생각하고 방법이 도저히 떠오르질 않는 것이다.
그래서 트리의 지름 자체를 구글링을 통해서 찾아보았다.
그런데, 방법은 의외로 간단했다.
-
임의의 정점을 지정해 BFS를 하고 가장 먼 정점을 찾는다.
-
그리고 찾아낸 정점에서 다시 가장 먼 정점을 찾으면 거리를 구할 수 있다.
이게 된다고? 이런 생각이 들어 테스트 케이스를 직접 만들어서 이것저것 해봤지만,
된다는 것이 허탈감이 느껴졌다...
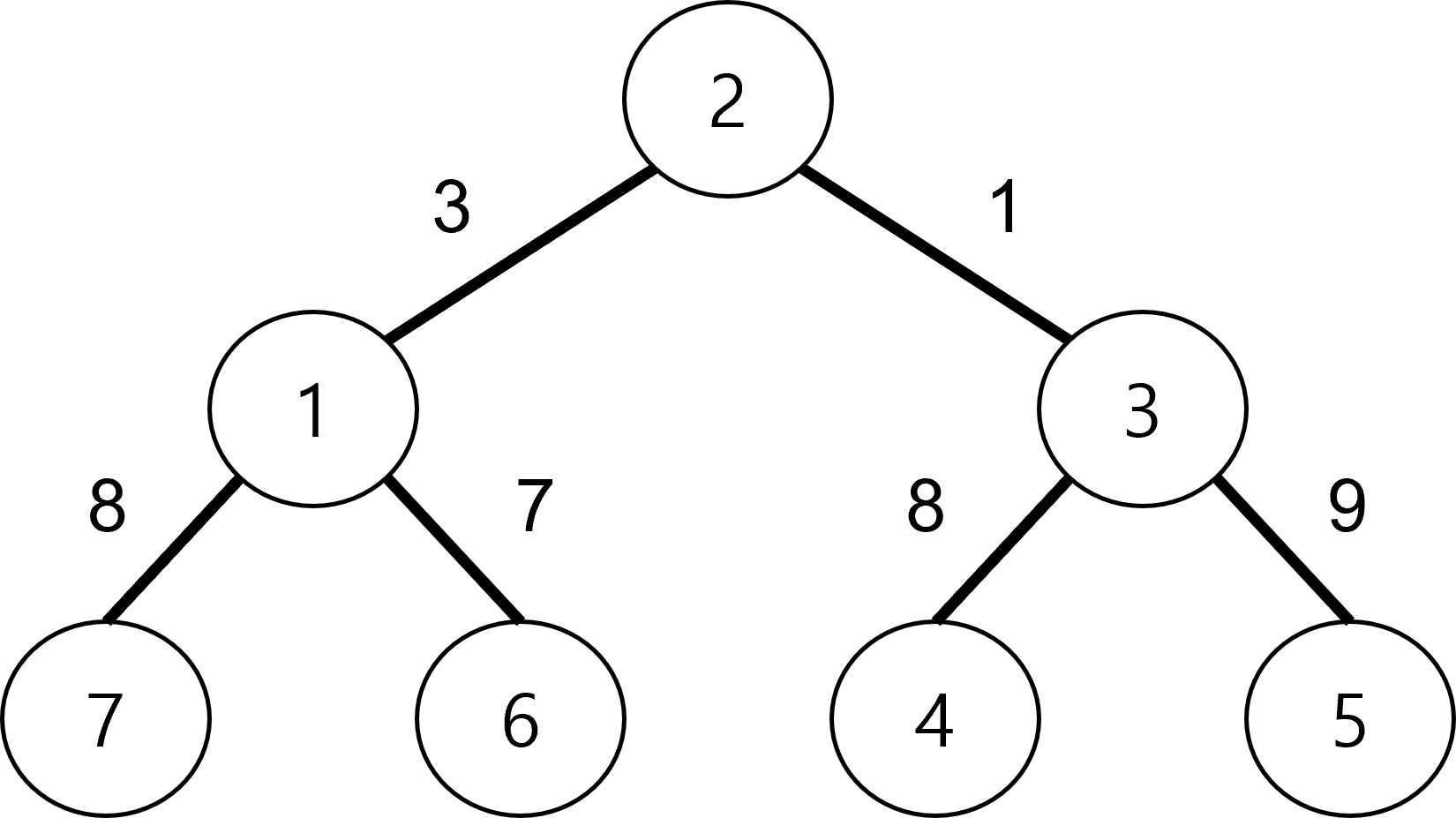
예제 테스트 케이스를 살펴보자.
7
1 2 3 7 8 6 7 -1
2 1 3 3 1 -1
3 2 1 4 8 5 9 -1
4 3 8 -1
5 3 9 -1
6 1 7 -1
7 1 8 -1
해당 테스트 케이스의 트리는 다음과 같이 구성된다.
모든 정점 별로 가장 먼 거리는 다음과 같다.
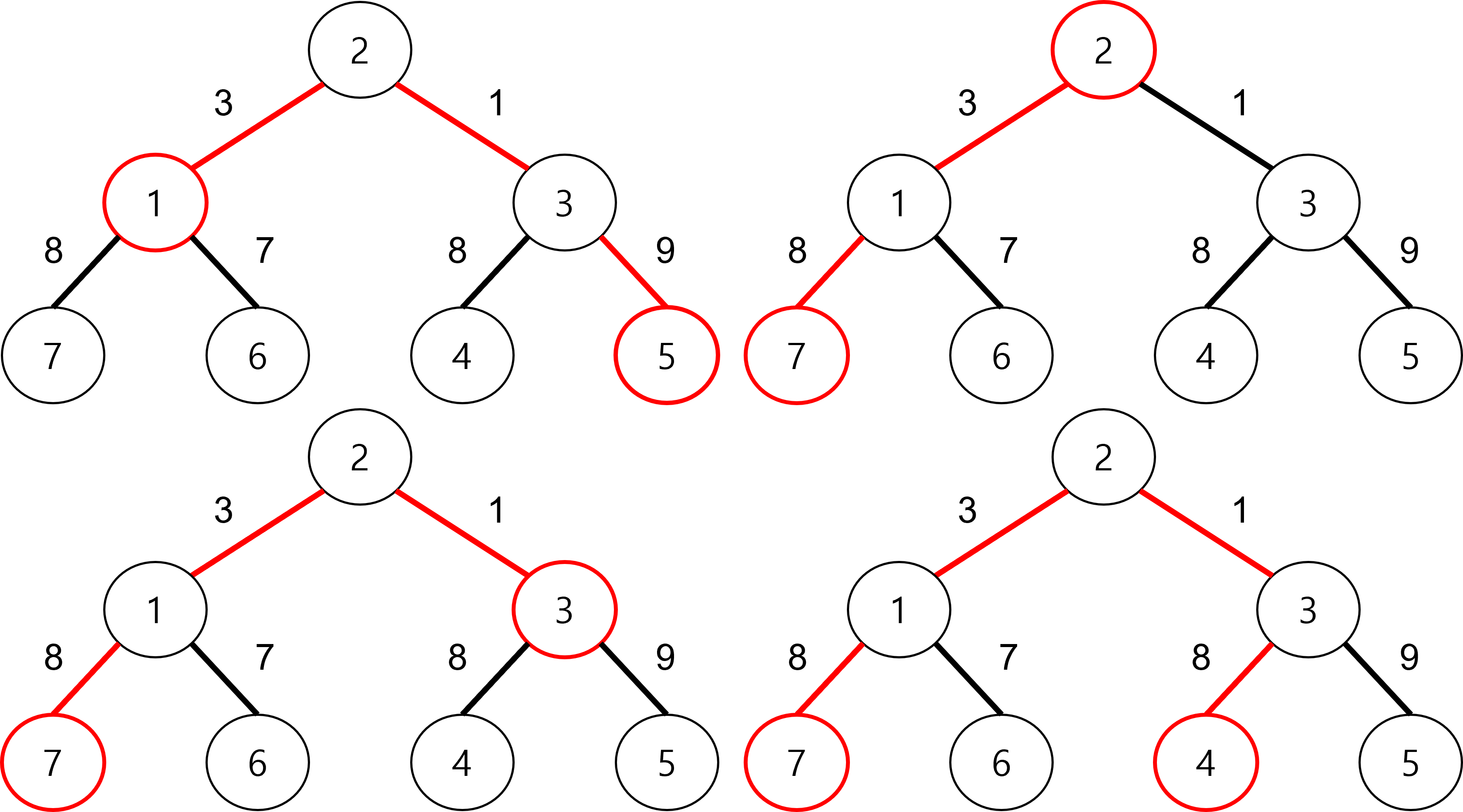
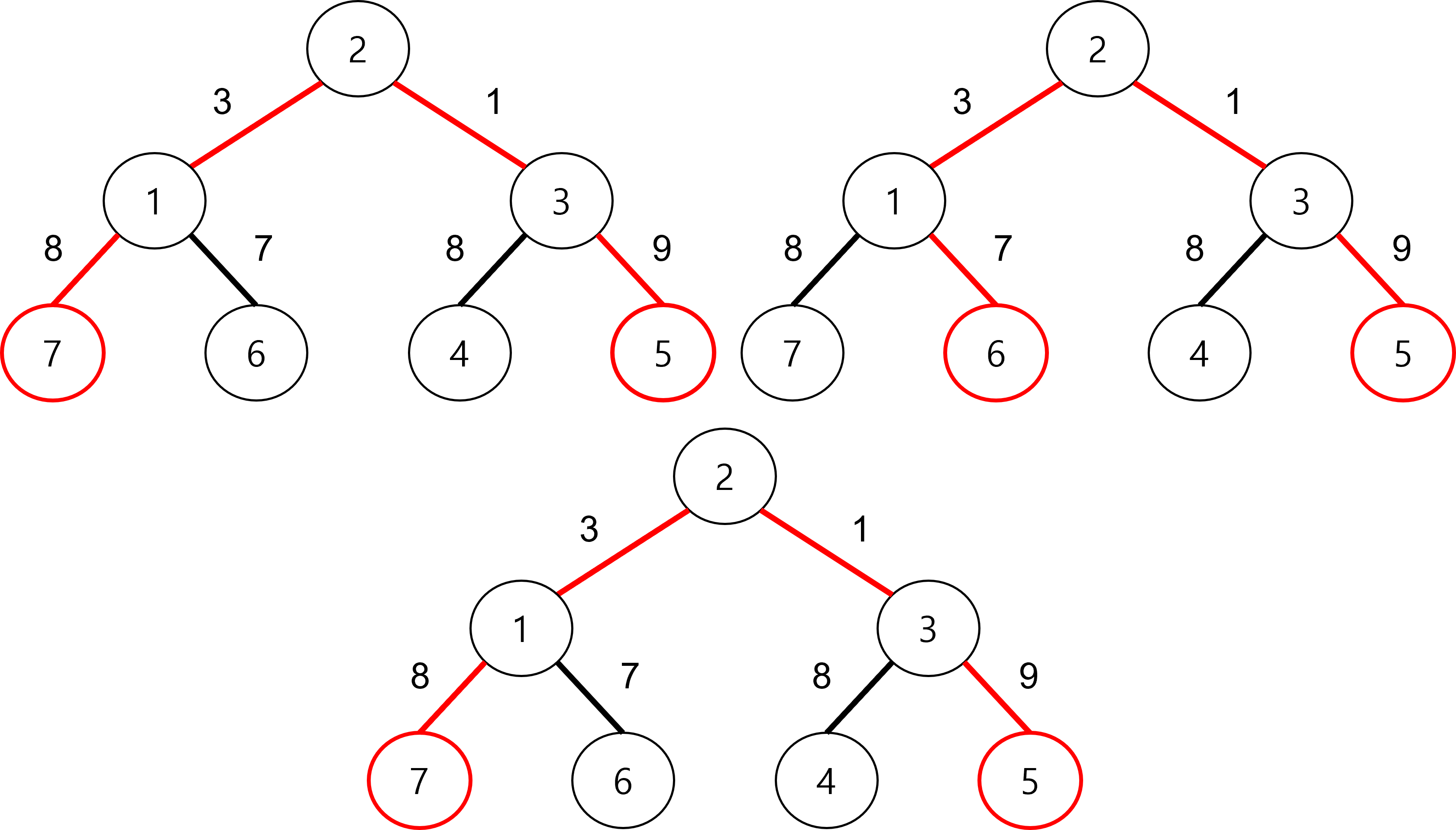
각 정점별로 가장 먼 정점을 고르면 5와 7에 도착하고,
5와 7은 서로 가장 먼 정점이므로,
특정 정점에서 BFS로 가장 먼 정점을 탐색한 뒤,
다시 한 번 가장 먼 정점을 탐색하면 트리의 지름을 구할 수 있다.
3. 소스코드
import sys
from collections import deque
input = sys.stdin.readline
def solution(V,tree):
answer = 0
count = [0] * (V+1)
count[1] = 1
q = deque([[1,0]])
start,start_cost = 0,0
while q:
now,total = q.popleft()
for edge in tree[now]:
end,cost = edge
if count[end] == 0:
q.append([end,cost+total])
count[end] = 1
else:
if start_cost < total:
start = now
start_cost = total
count = [0] * (V+1)
count[start] = 1
q = deque([[start,0]])
while q:
now,total = q.popleft()
for edge in tree[now]:
end,cost = edge
if count[end] == 0:
q.append([end,cost+total])
count[end] = 1
else:
if answer < total:
answer = total
return answer
if __name__ == "__main__":
V = int(input())
tree = dict()
for _ in range(V):
line = list(map(int,input().split()))
tree[line[0]] = []
for i in range(1,len(line)-1,2):
tree[line[0]].append([line[i],line[i+1]])
print(solution(V,tree))4. 후기
이 문제를 처음 봤을 때는 트리에 도착할 때마다 무슨 가중치를 넣어야 하나
여러 생각으로 고민을 했던거 같다..
너무 간단하게 해결되니 허탈하다.
