[백준 1450번] 냅색문제

mokomoko·2021년 12월 30일

python 백준

1. 문제

세준이는 N개의 물건을 가지고 있고, 최대 C만큼의 무게를 넣을 수 있는 가방을 하나 가지고 있다.

N개의 물건을 가방에 넣는 방법의 수를 구하는 프로그램을 작성하시오.

제한 사항

시간 : 1 초
메모리 : 128 MB

입력

첫째 줄에 N과 C가 주어진다. N은 30보다 작거나 같은 자연수, C는 10^9보다 작거나 같은 음이 아닌 정수이다. 둘째 줄에 물건의 무게가 주어진다. 무게도 10^9보다 작거나 같은 자연수이다.

출력

첫째 줄에 가방에 넣는 방법의 수를 출력한다.

- 키워드

MITM( Meet in the middle ) 알고리즘을 사용하자

총 4단계의 과정을 거친다. (리스트 반갈죽 -> 조합 -> 정렬 -> 이분 탐색)

2. 풀이

예제 테스트케이스는 다음과 같이 설정했다.

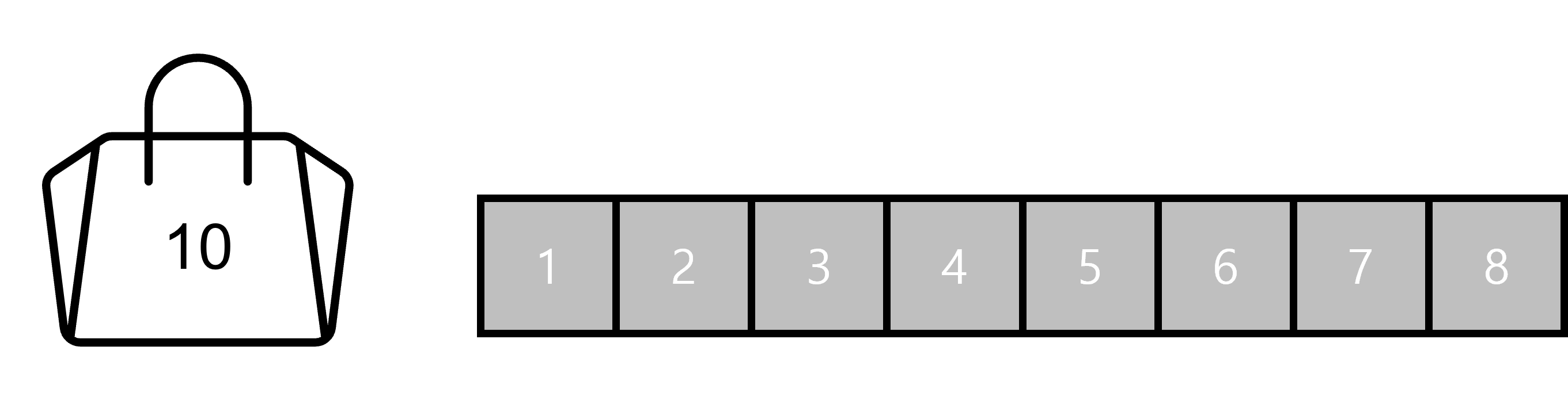
1. 리스트 반갈죽

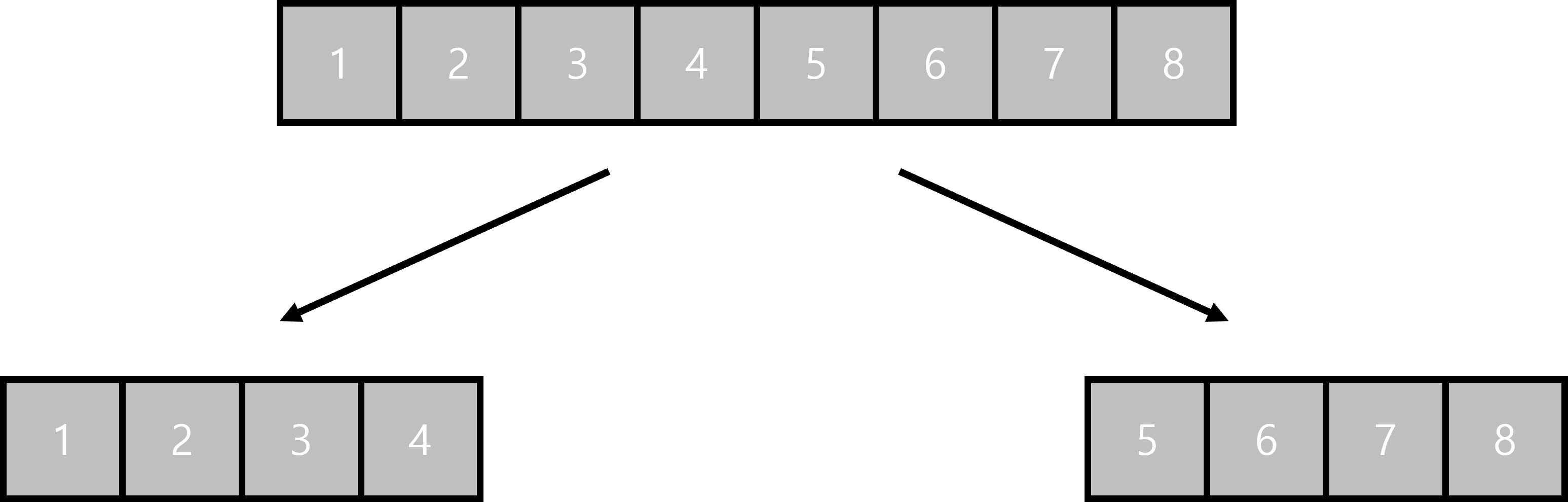
말그대로 2개의 리스트로 반갈죽 하면 된다.

2. 조합

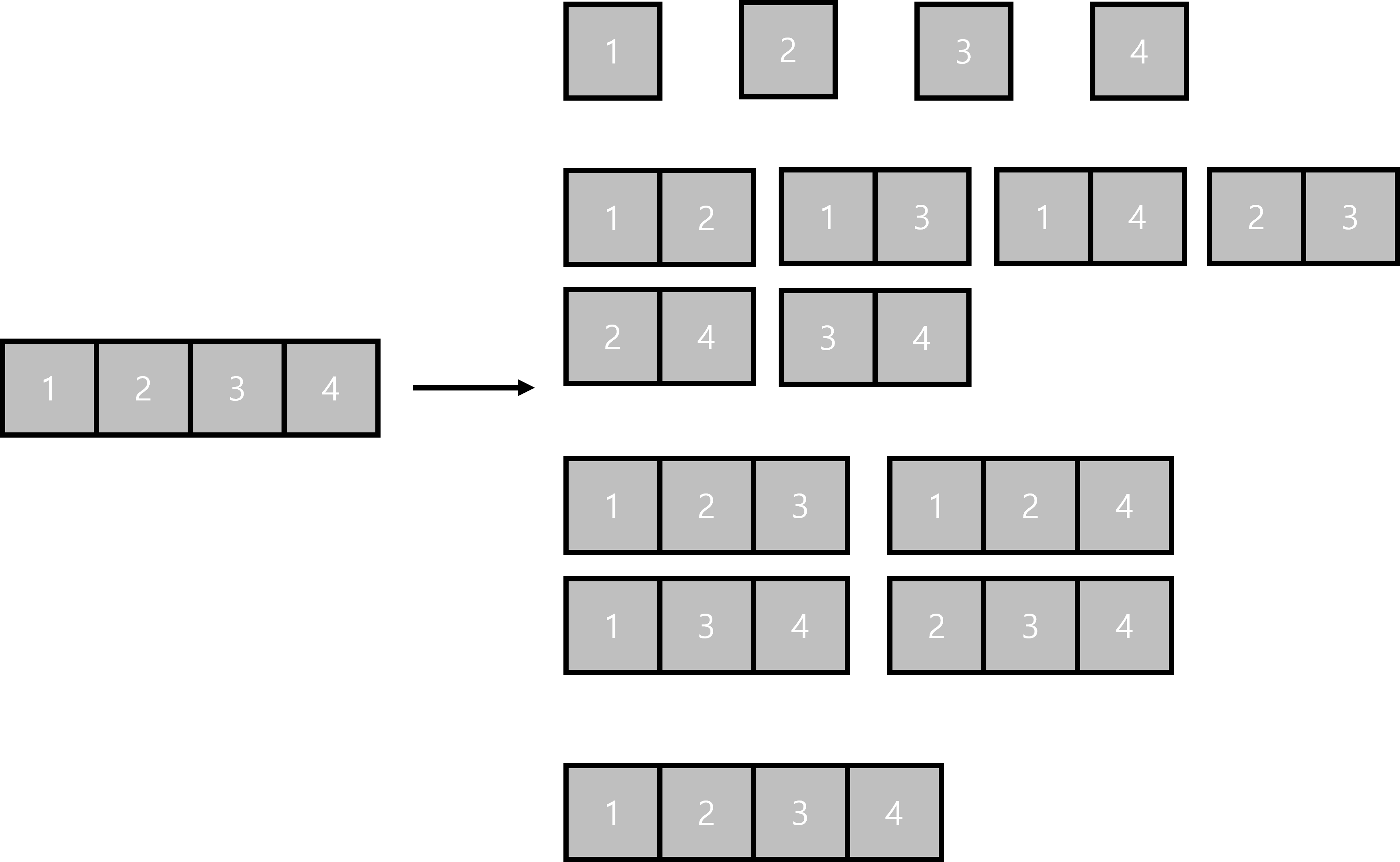
Python에서는 itertools의 combinations를 이용하면 된다.

다른 언어에서는 사용 가능한 라이브러리가 있다면 참고하도록 하자.

해당 조합들의 합을 리스트화 시킨다.

3. 정렬

위에서 조합으로 나온 리스트를 정렬한다.

4번의 과정을 거치기 전에 반갈죽한 다른 리스트도 같은 과정을 거치도록 하자.

여기서 0이 들어가 있는데, 0이 들어간 이유는

아무것도 넣지 않는 경우의 수도 고려하기 위함이다.

4. 이분탐색

한 쪽 리스트의 값을 기준으로 이분 탐색을 진행한다.

첫 번째 이분탐색이다.

오른쪽에서 아무 물건도 넣지 않는 경우의 수이다.

그러므로 가장 큰 경우의 수 까지 모두 가방에 넣을 수 있다. ( answer += 16 )

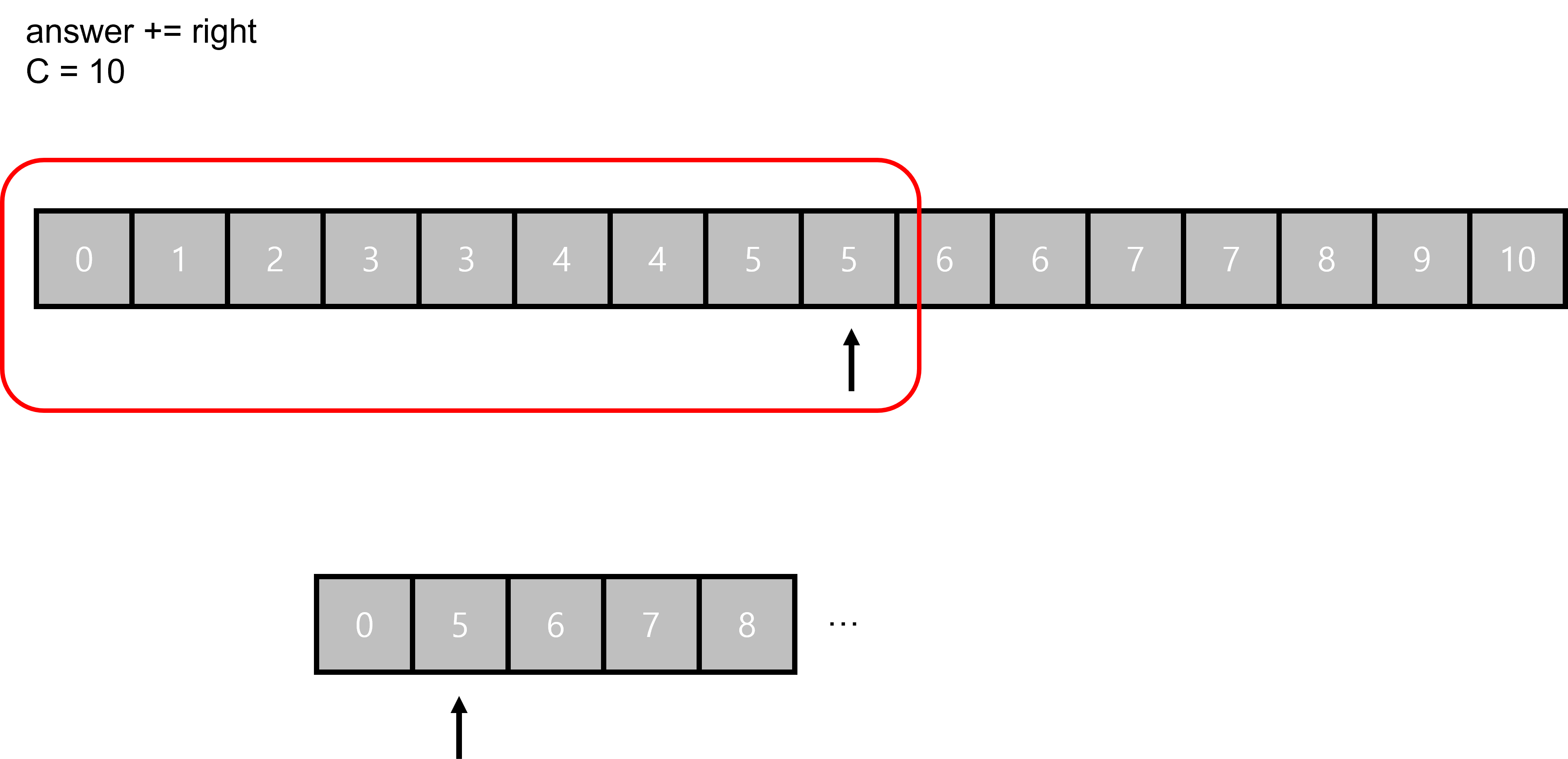
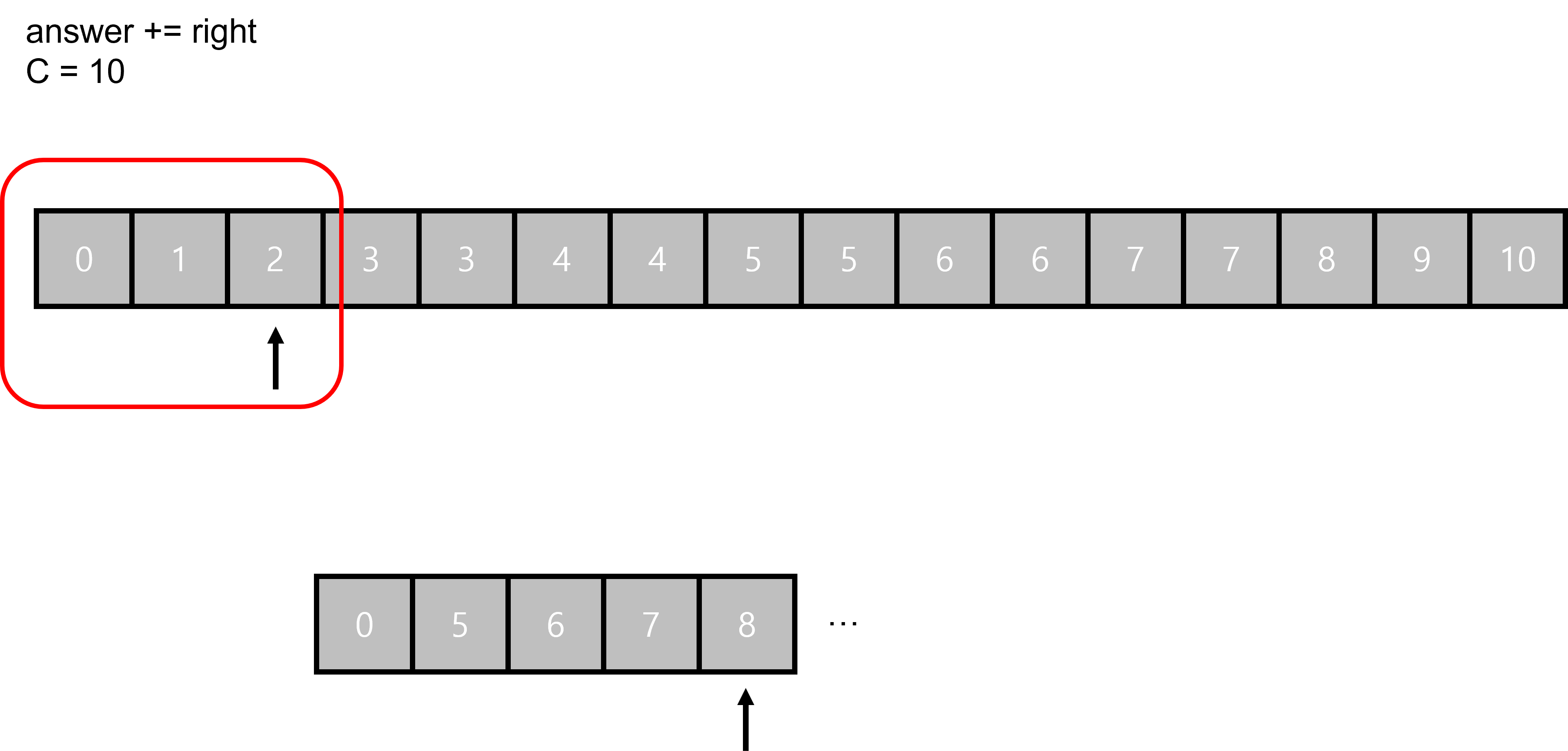
두 번째는 무게가 5인 물건을 넣는 경우의 수다.

이 때 왼쪽에 있는 경우의 수 중 최대 5가 나오는 경우의 수까지만 넣을 수 있다.

그러므로 answer에 9를 더하게 된다.

이 과정을 계속 진행한다.

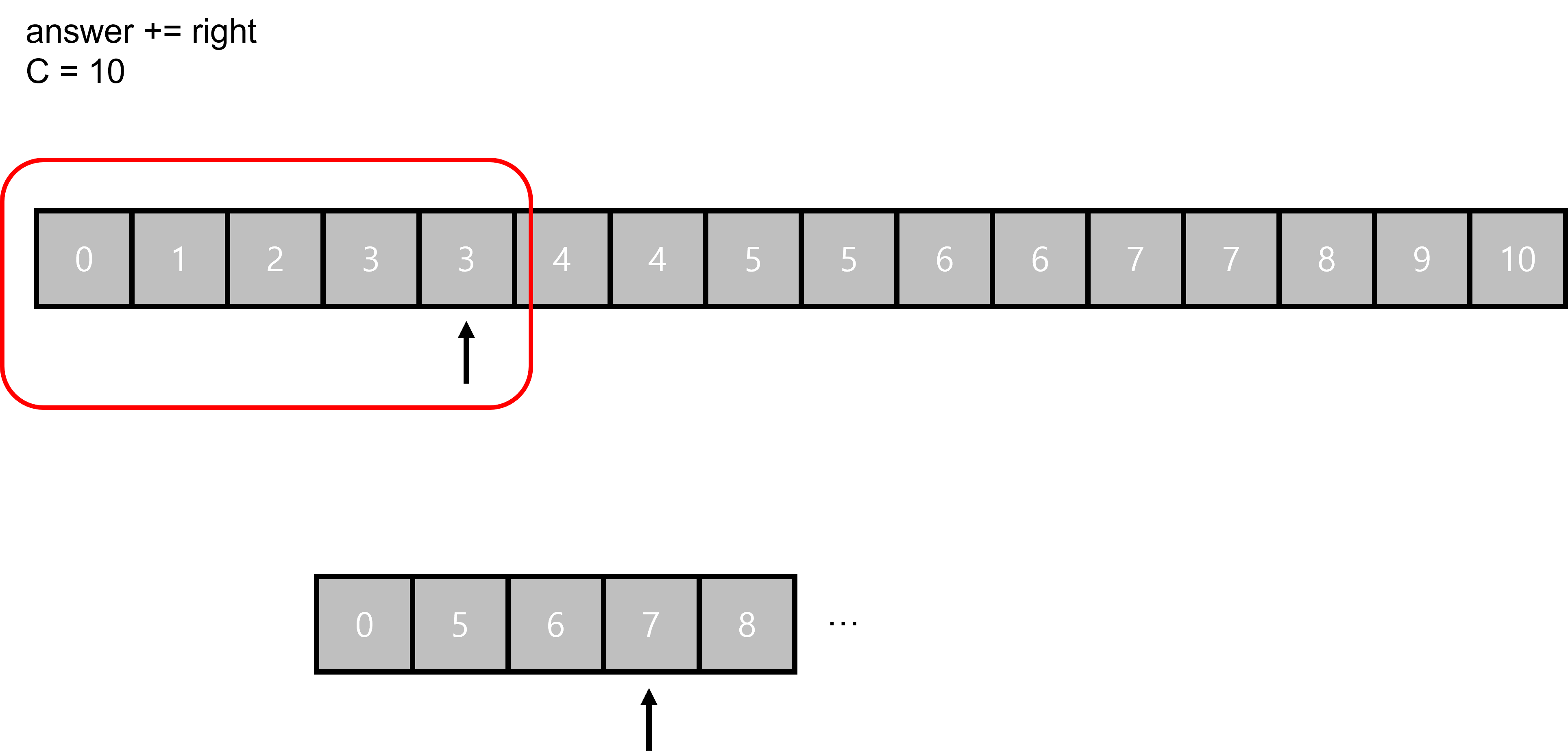
만일 오른쪽 경우의 수 중 배낭의 무게를 이미 초과했다면

해당 경우의 수는 0이므로 패스한다.

본 테스트케이스의 answer는 40이다.

3. 소스코드

import sys
from itertools import combinations
input = sys.stdin.readline

# MITM (Meet in the middle) Algorithm
def solution(N,C,m):
	if N == 1 and m[0] <= C:
		return 2
	if N == 1 and m[0] > C:
		return 1

	left_m,right_m = m[:N//2], m[N//2:]
	sub_left,sub_right = [0],[0]
	
	for i in range(1,len(left_m)+1):
		for sub in combinations(left_m,i):
			sub_left.append(sum(sub))
	sub_left = sorted(sub_left)

	for i in range(1,len(right_m)+1):
		for sub in combinations(right_m,i):
			sub_right.append(sum(sub))
	sub_right = sorted(sub_right)
	answer = 0
	for i in sub_right:
		if i > C:
			continue
		left = 0
		right = len(sub_left)
		while left < right:
			mid = (left+right) // 2
			if sub_left[mid]+i > C:
				right = mid
			else:
				left = mid+1
		answer += right

	return answer

if __name__ == "__main__":
	N,C = map(int,input().split())
	m = list(map(int,input().split()))
	print(solution(N,C,m))