[백준 1504번] 특정한 최단 경로

mokomoko·2022년 1월 10일

1. 문제

방향성이 없는 그래프가 주어진다. 세준이는 1번 정점에서 N번 정점으로 최단 거리로 이동하려고 한다. 또한 세준이는 두 가지 조건을 만족하면서 이동하는 특정한 최단 경로를 구하고 싶은데, 그것은 바로 임의로 주어진 두 정점은 반드시 통과해야 한다는 것이다.

세준이는 한번 이동했던 정점은 물론, 한번 이동했던 간선도 다시 이동할 수 있다. 하지만 반드시 최단 경로로 이동해야 한다는 사실에 주의하라. 1번 정점에서 N번 정점으로 이동할 때, 주어진 두 정점을 반드시 거치면서 최단 경로로 이동하는 프로그램을 작성하시오.

제한 사항

시간 : 1 초
메모리 : 256 MB

입력

첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000)
둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데, a번 정점에서 b번 정점까지 양방향 길이 존재하며, 그 거리가 c라는 뜻이다. (1 ≤ c ≤ 1,000)
다음 줄에는 반드시 거쳐야 하는 두 개의 서로 다른 정점 번호 v1과 v2가 주어진다.
(v1 ≠ v2, v1 ≠ N, v2 ≠ 1)

출력

첫째 줄에 두 개의 정점을 지나는 최단 경로의 길이를 출력한다.
그러한 경로가 없을 때에는 -1을 출력한다.

- 키워드

다익스트라 알고리즘을 사용하자

다익스트라를 구현한 뒤 여러 번 사용해 경로를 탐색

2. 풀이

다익스트라 알고리즘은 특정 그래프에서 최단경로를 구할 때 사용하는 알고리즘이다.

이번 문제에서는 중간에 거쳐야 할 노드가 2개가 있지만,

그냥 다익스트라 알고리즘을 3번 쓰는 것일 뿐이다.

예제 테스트케이스를 살펴보자.

7 10
1 2 10
1 3 11
2 3 20
2 4 30
3 4 100
3 5 100
4 6 20
5 6 20
5 7 200
6 7 10
3 5

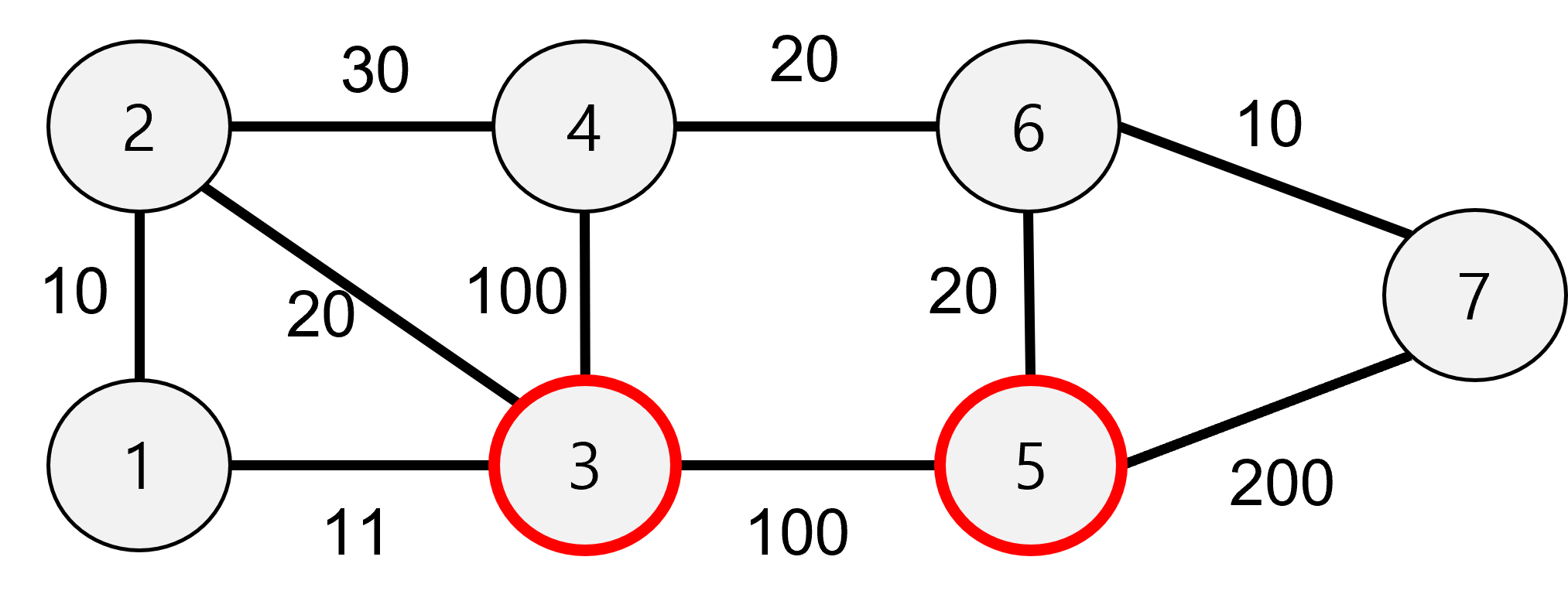
도착 지점은 빨간색으로 3,5 이며, 출발 지점은 1이다.

먼저, 1에서 도달 할 수 있는 곳은 2,3이 있다.

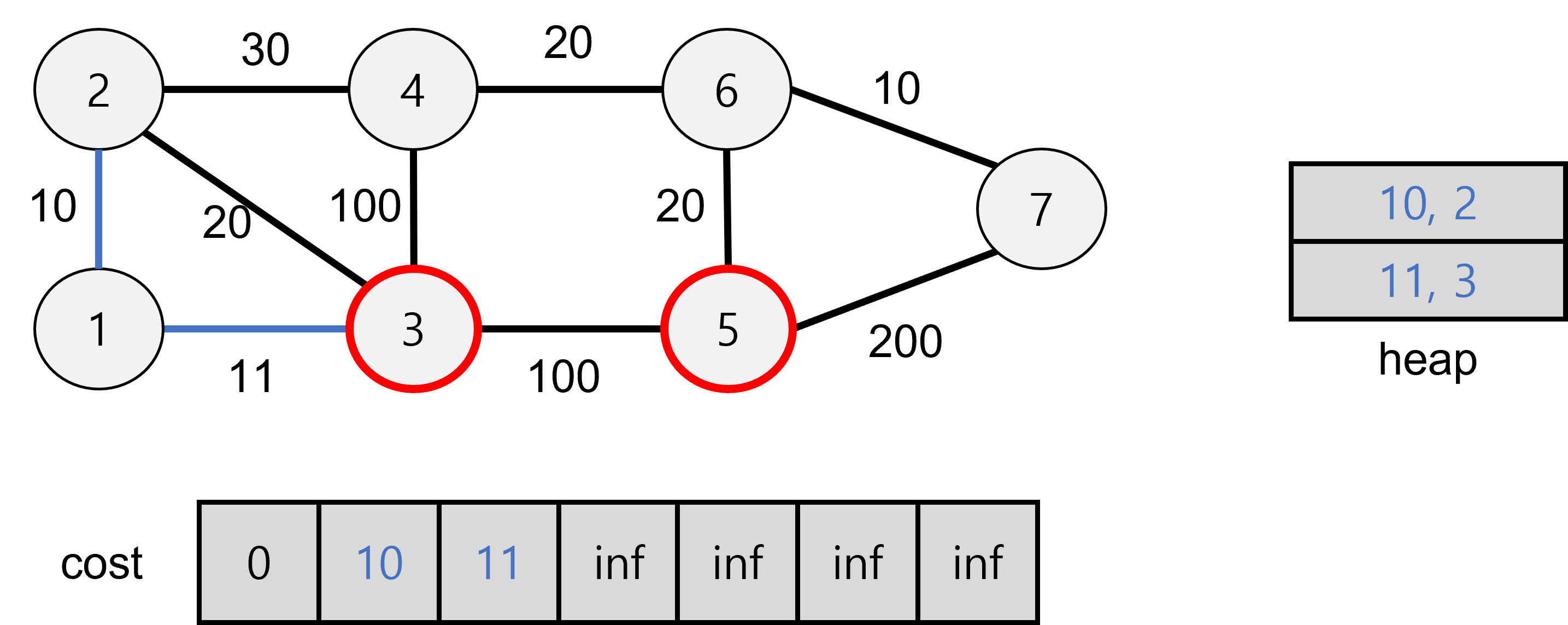
그 다음 경로를 탐색하기 위해서 heap에서 다음 탐색지를 가져온다.

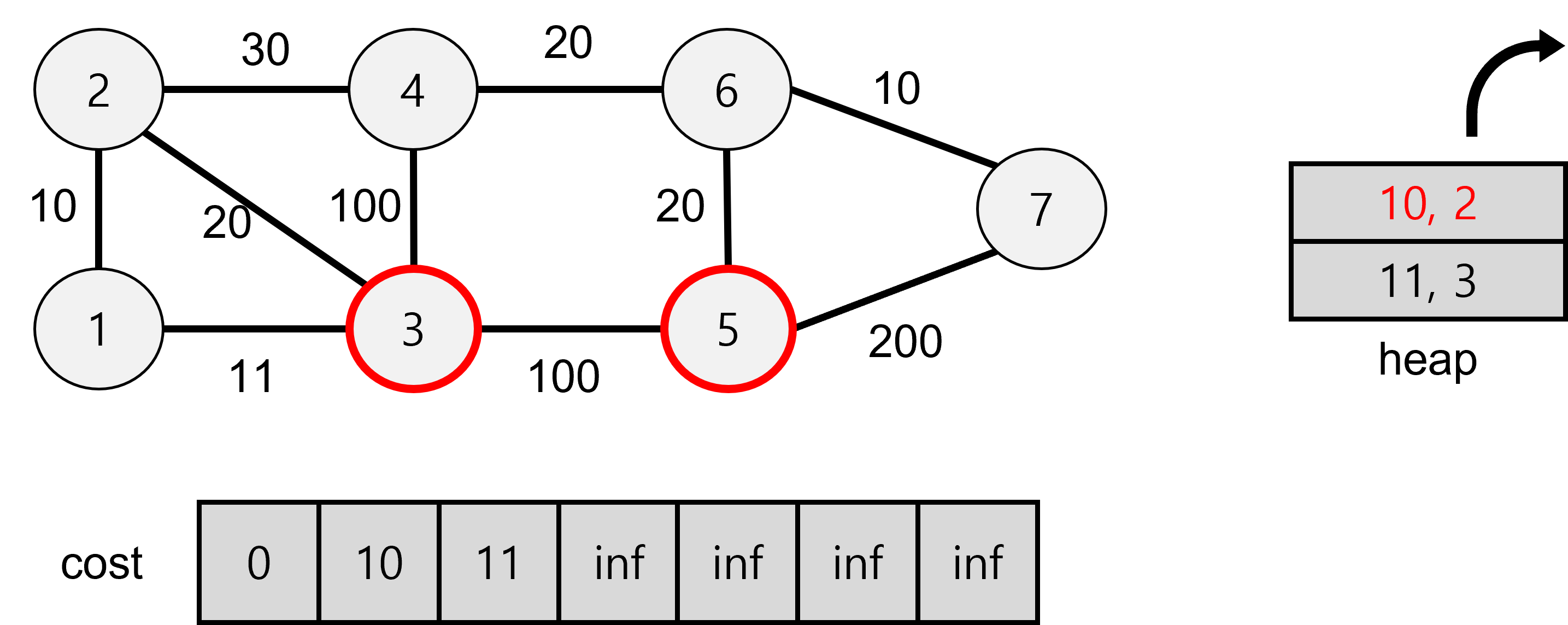
다음 탐색은 2에서 도달할 수 있는 곳을 탐색한다.

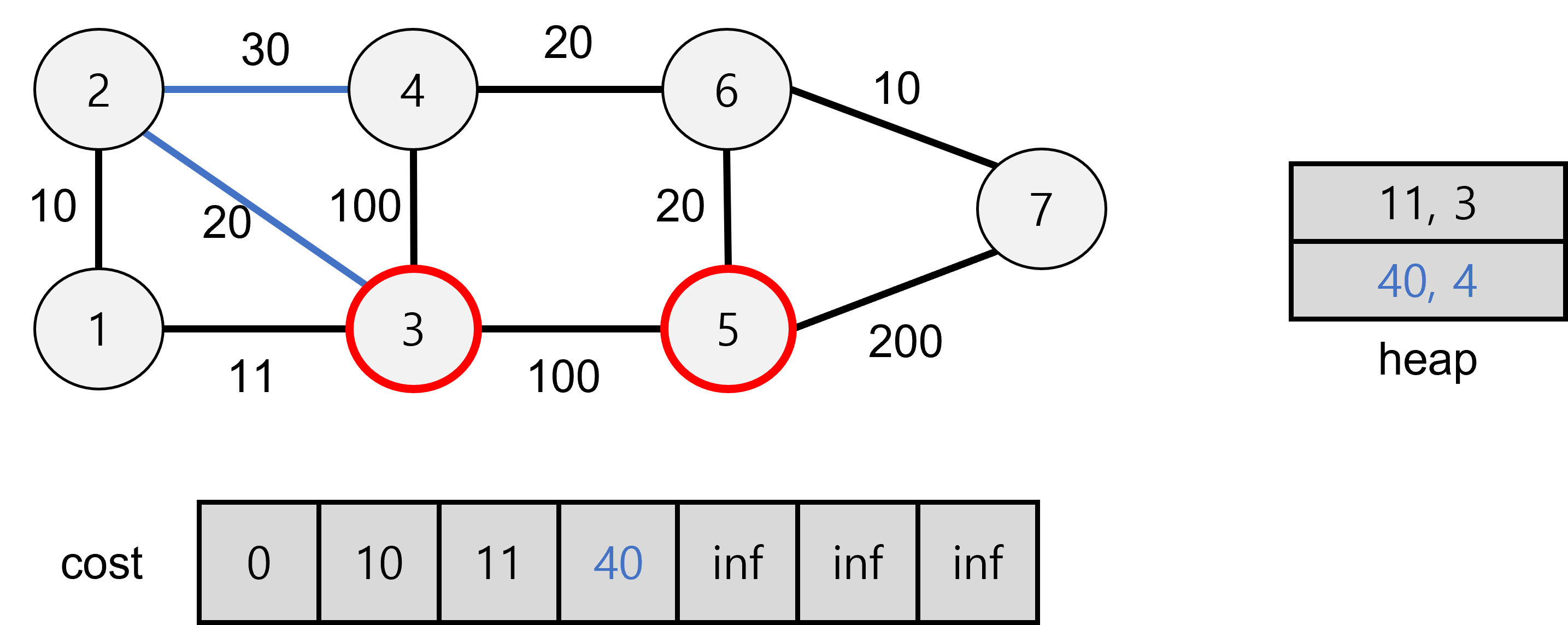
3과 4가 있으나

cost에 저장된 값 11이 10+20보다 작기 때문에 heap에 저장하지 않는다.

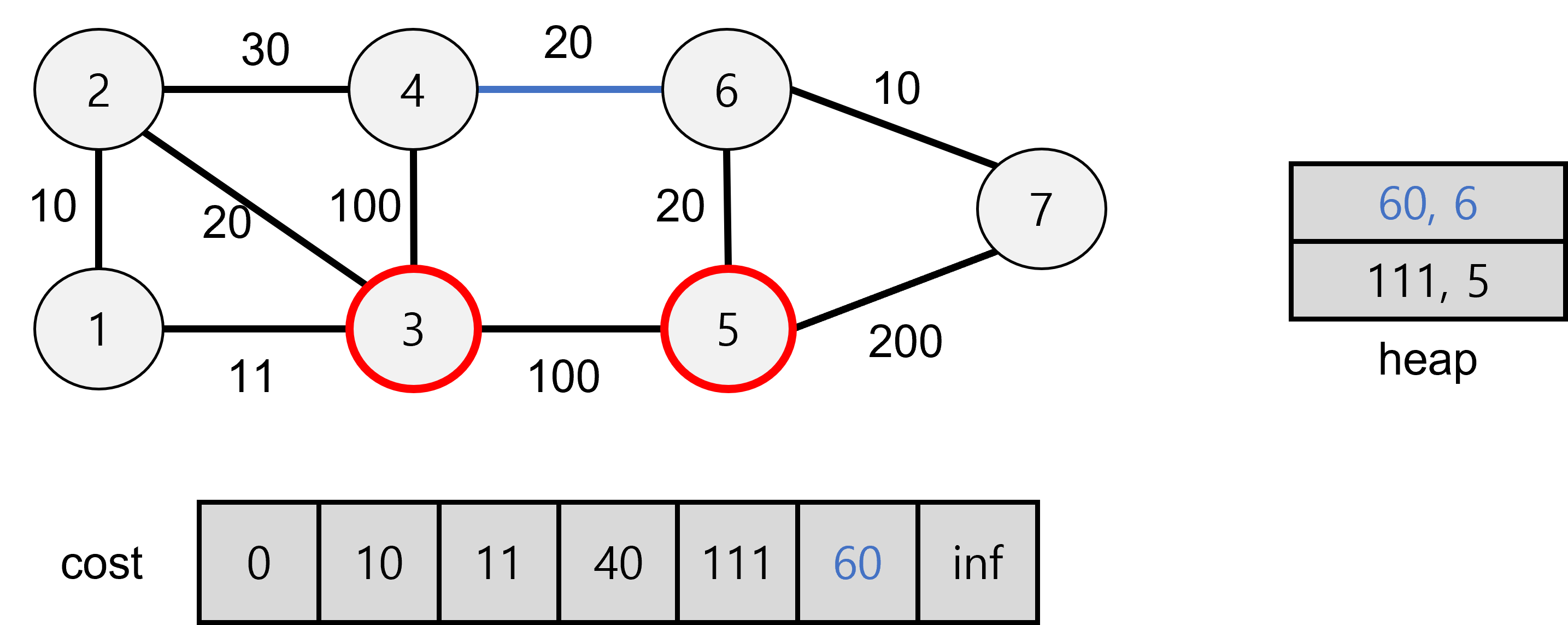
계속 이와 같은 과정을 거쳐 탐색을 거친다.

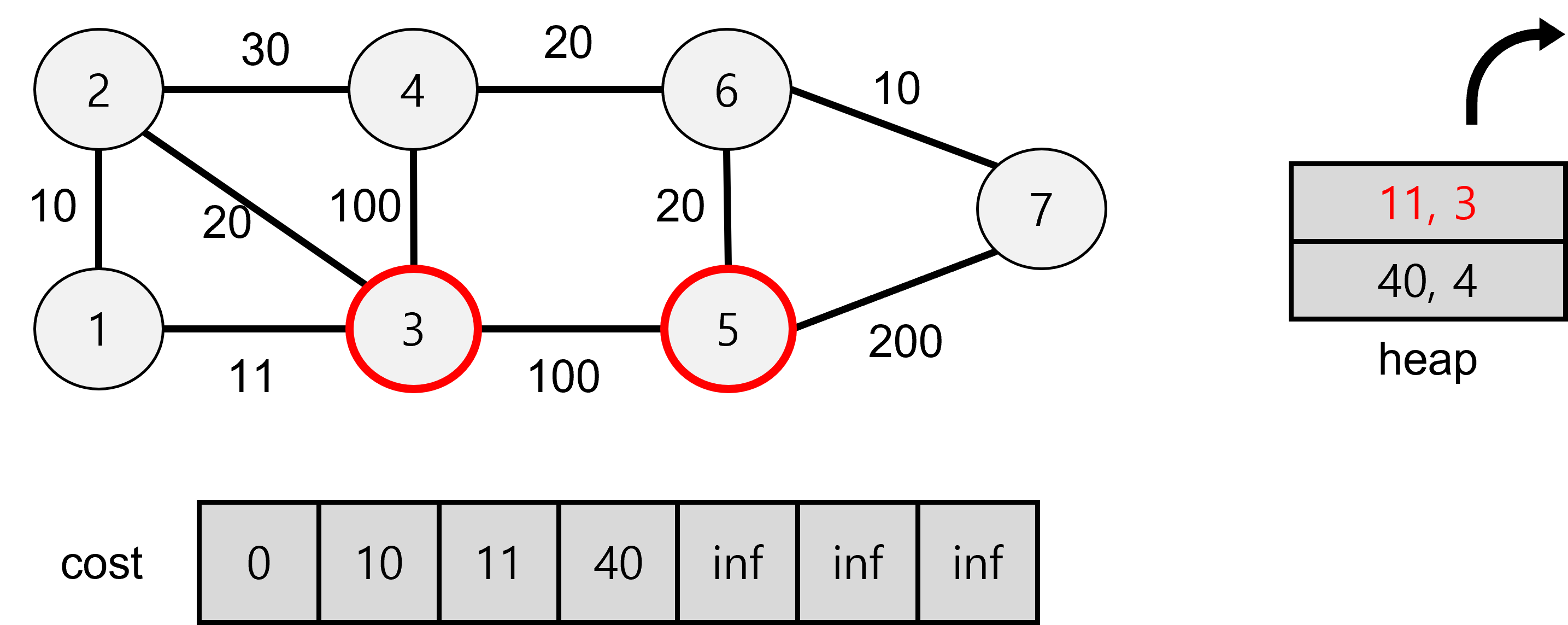
3에서 탐색했으나, 4로 가는 값은 40이 더 작아서 heap에 저장되지 않고,

최초 탐색인 5는 111값을 heap에 저장한다.

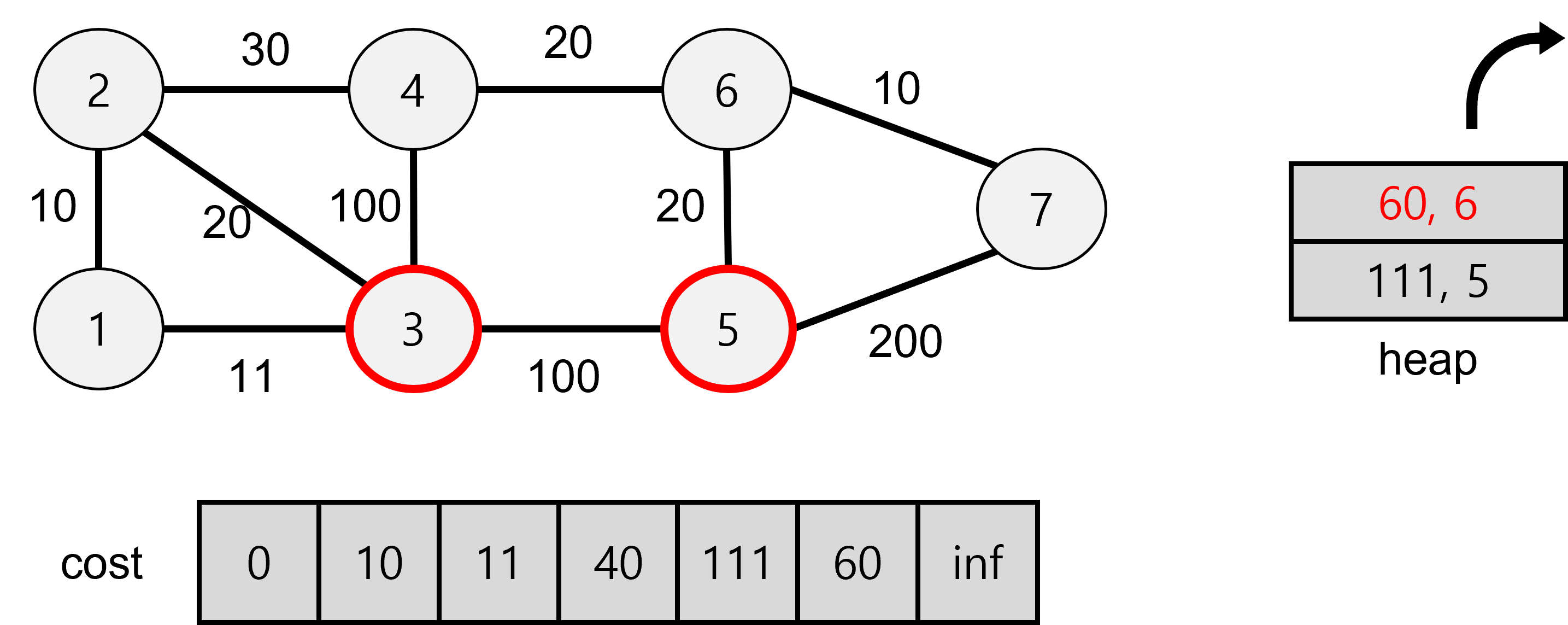
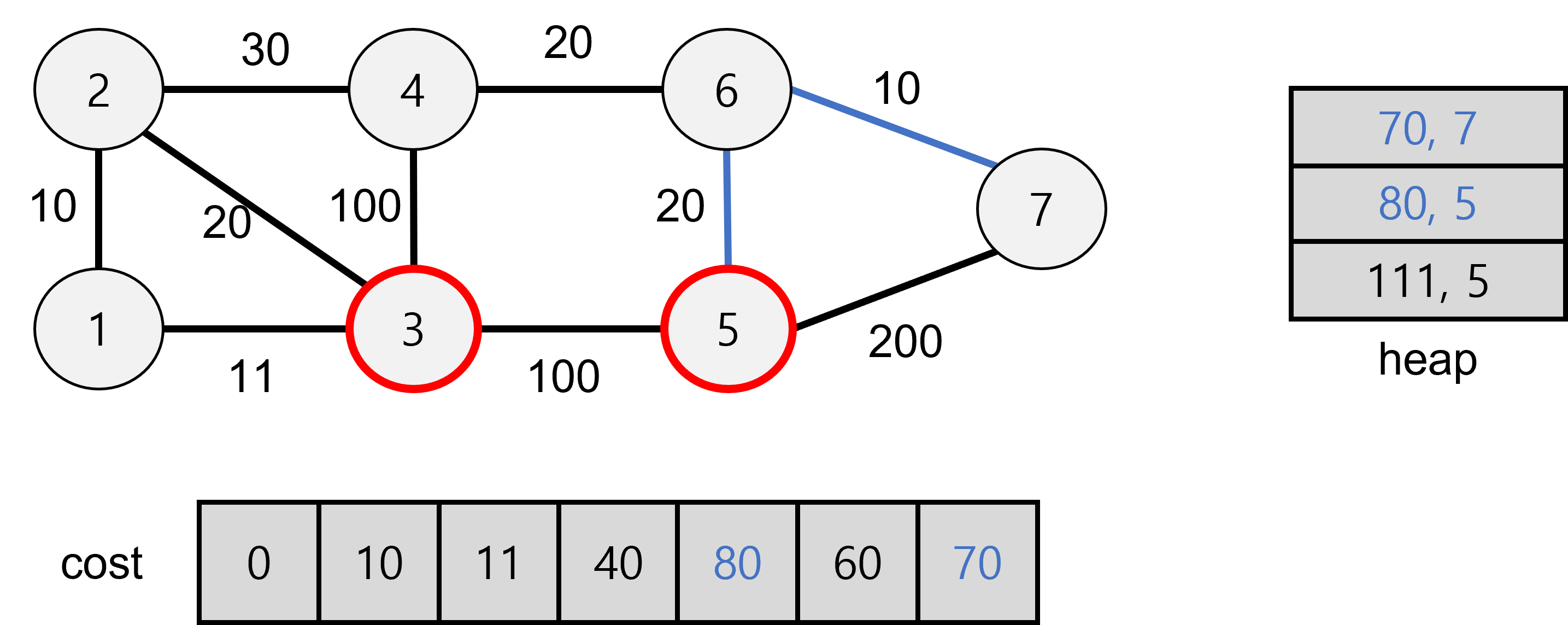
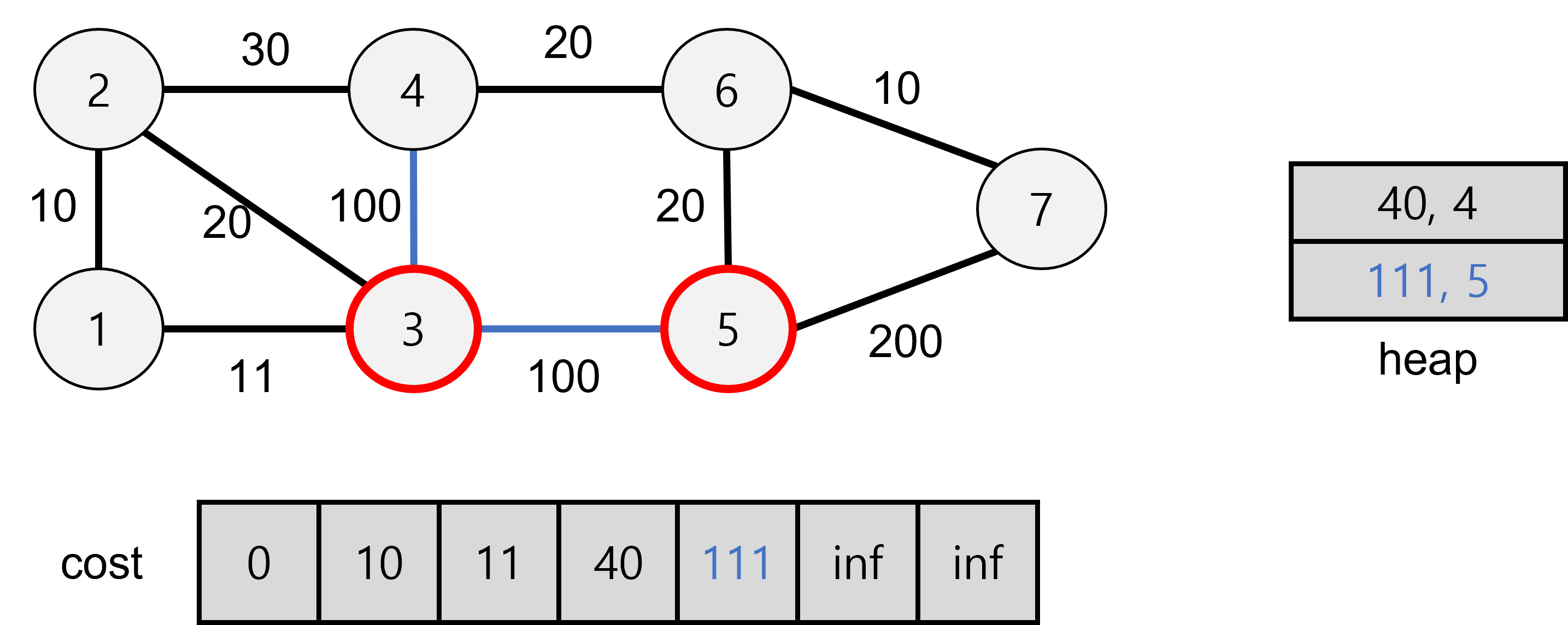
해당 과정에서 5로 가는 경로가 있으나 111보다 cost값이 낮으므로

heap과 cost에 새로 저장해준다.

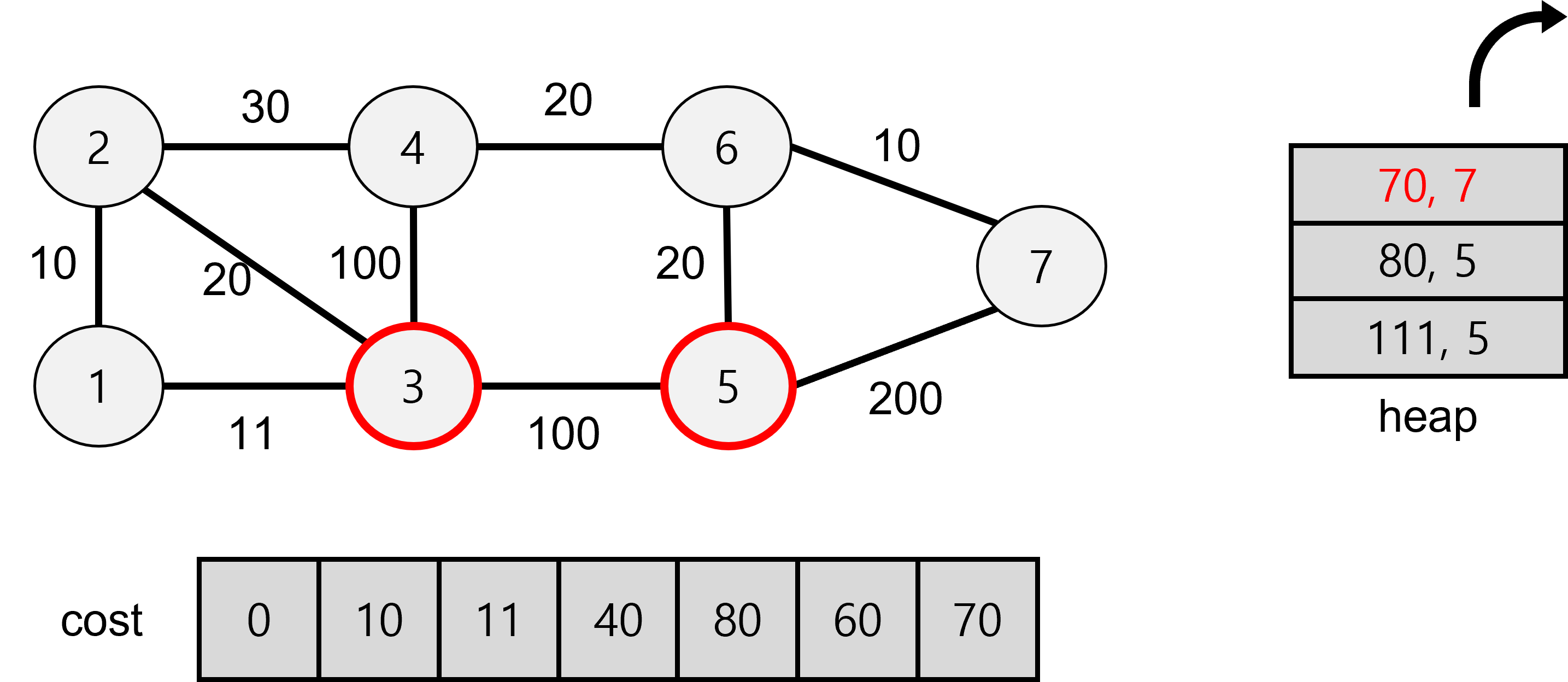
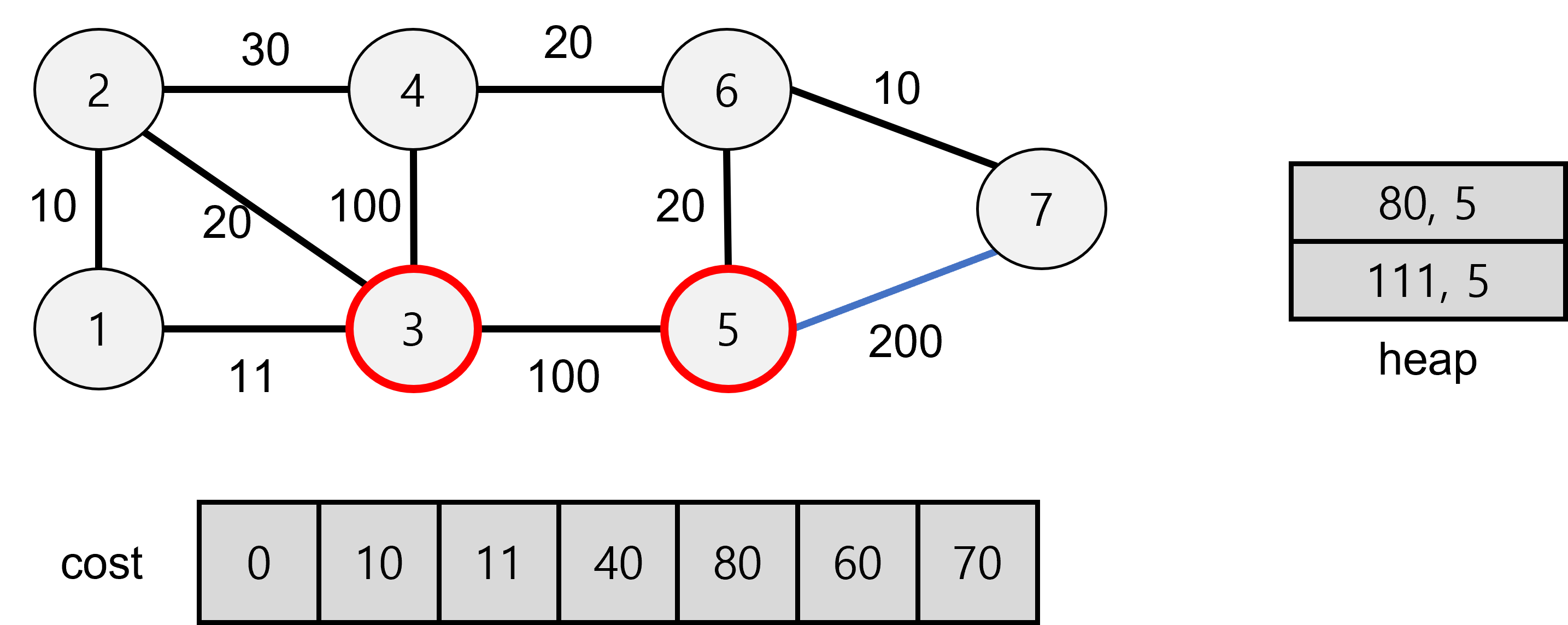
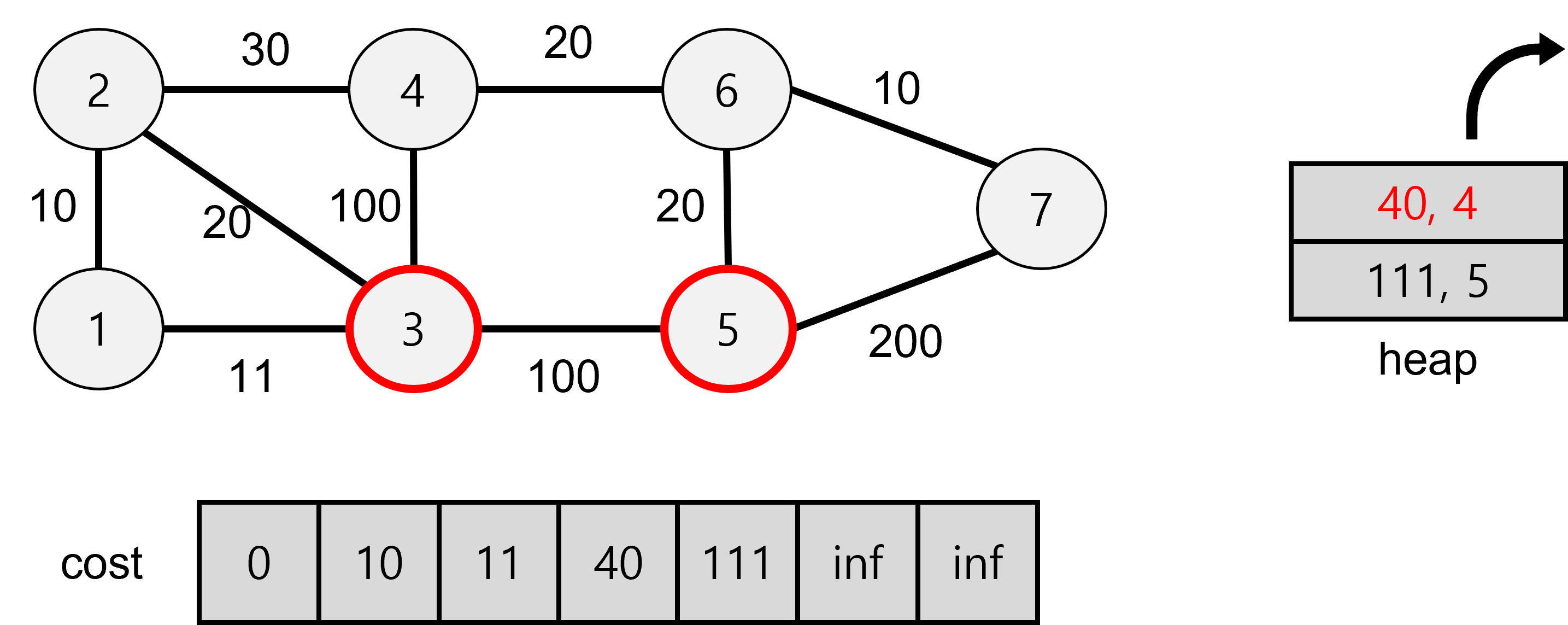
7에서 5로 탐색할 경우 270이 나오므로 기존 값보다 커서 저장하지 않는다.

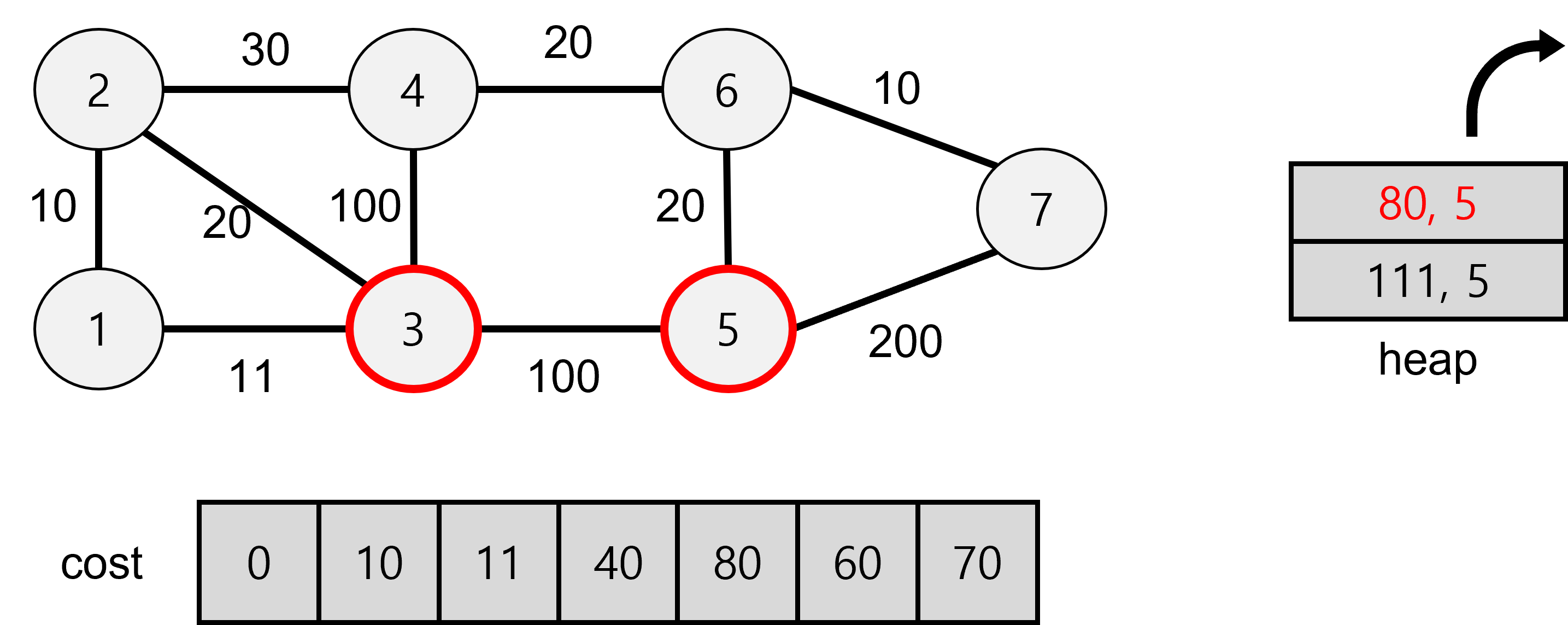
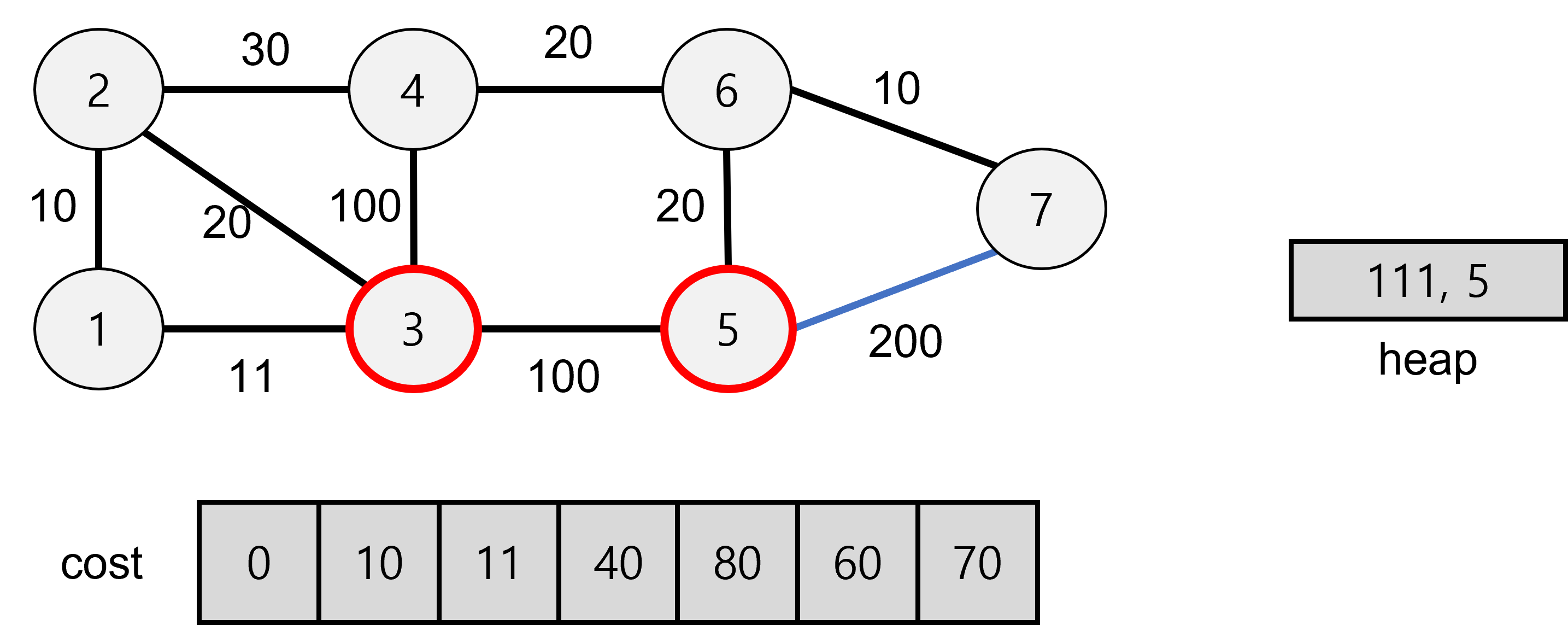
5에서 7로 탐색할 경우 280이 나오므로 기존 값보다 커서 저장하지 않는다.

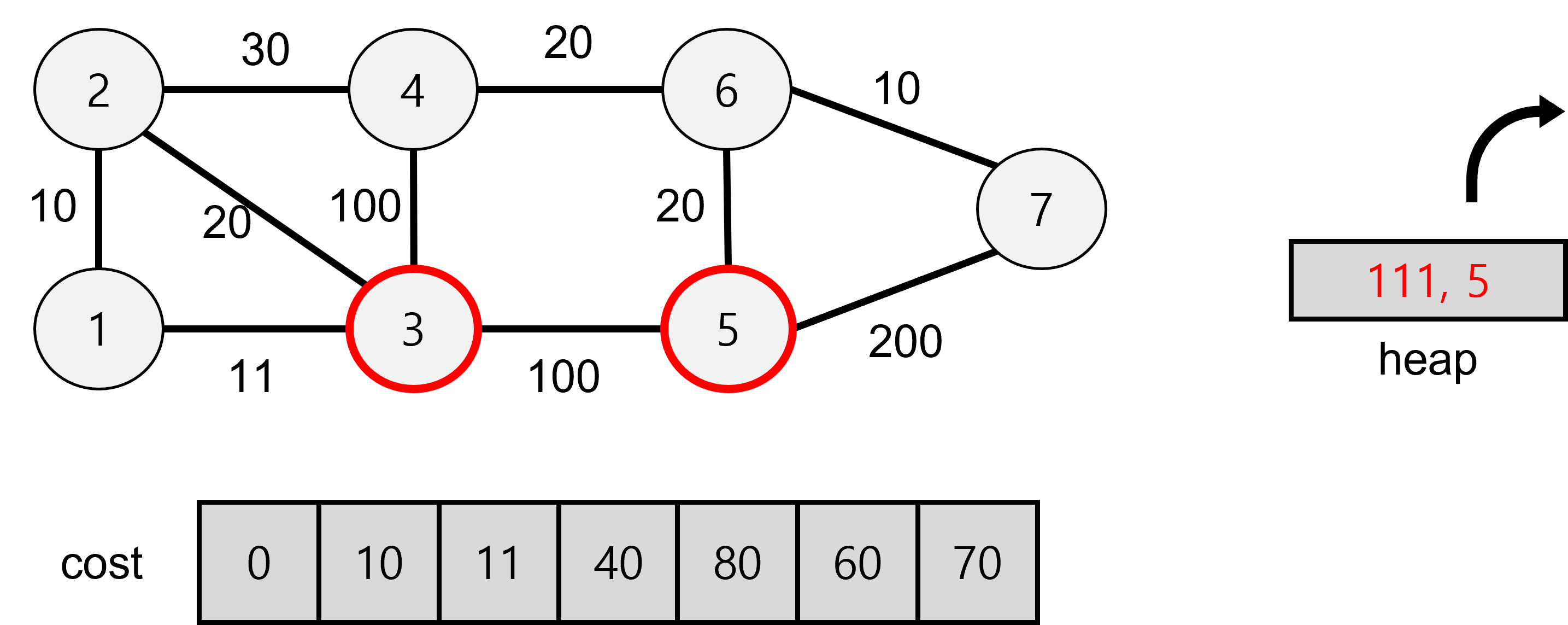
기존 5의 값이 heap에 저장된 111보다 작으므로 탐색을 하지 않는다.

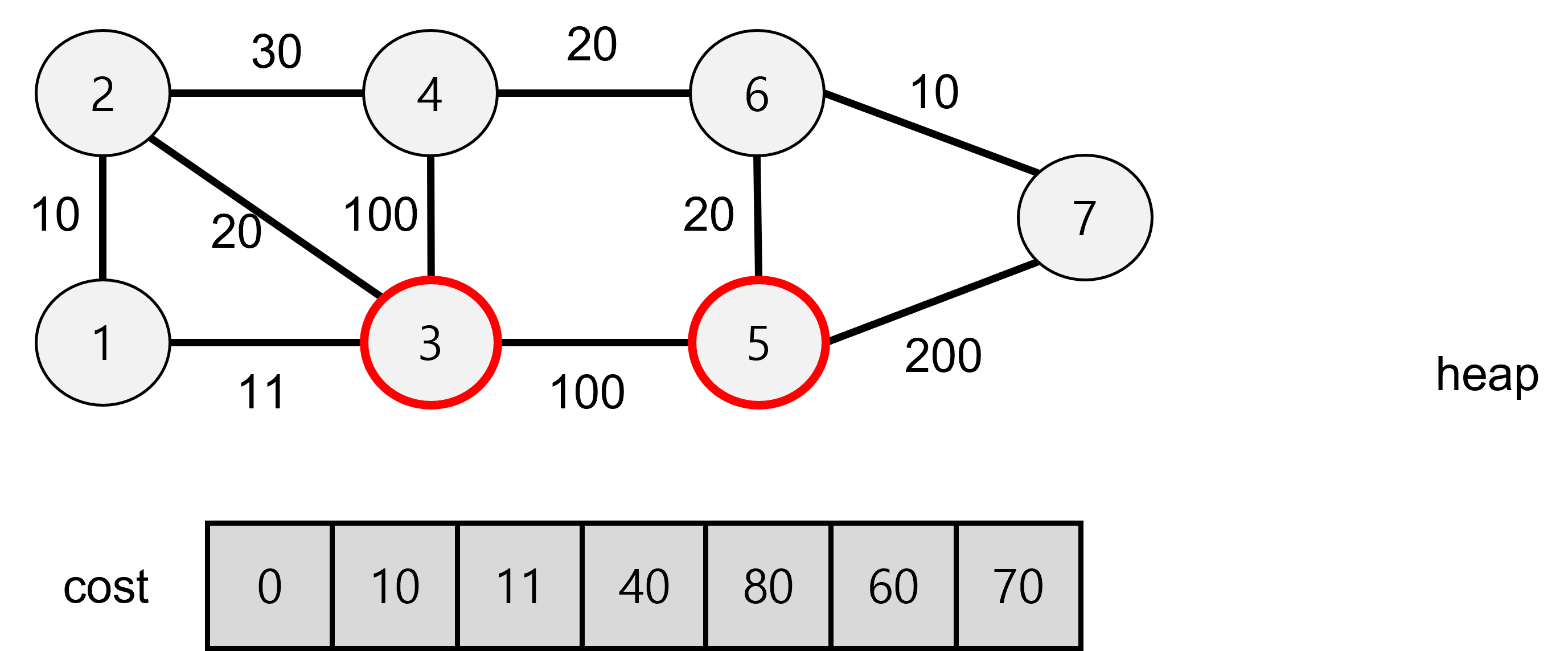
heap이 비어있으므로 탐색을 중단하고

1에서 출발할 경우 중간 도착지점인 3 또는 5를 return한다.

해당 소스코드에선 다익스트라를 총 6번 사용하지만,

실질적으로는 3->5, 5->3이 같기 때문에 최소 5번을 사용해야 한다.

다익스트라를 1 -> 3 -> 5 -> 7 혹은 1 -> 5 -> 3 -> 7 을 진행했을 때,

더 짧은 값을 반환하면 된다.

3. 소스코드

import sys
import heapq
input = sys.stdin.readline

def search(V,start,end,graph):
	answer = 0
	length = [1e9] * (V+1)
	length[start] = 0
	q = [(start,0)]
	while q:
		now,value = heapq.heappop(q)
		if length[now] < value:
			continue

		for edge in graph[now]:
			e,v = edge
			if v+value < length[e]:
				heapq.heappush(q,(e,v+value))
				length[e] = v+value

	return length[end]

def solution(V,E,edges,must):
	graph = dict()
	for i in range(1,V+1):
		graph[i] = []
	for edge in edges:
		heapq.heappush(graph[edge[0]],(edge[1],edge[2]))
		heapq.heappush(graph[edge[1]],(edge[0],edge[2]))
	length_A = search(V,1,must[0],graph.copy()) + search(V,must[0],must[1],graph.copy()) + search(V,must[1],V,graph.copy())
	length_B = search(V,1,must[1],graph.copy()) + search(V,must[1],must[0],graph.copy()) + search(V,must[0],V,graph.copy())
	if length_A >= 1e9 and length_B >= 1e9:
		return -1
	else:
		return min(length_A,length_B)

if __name__ == "__main__":
	V,E = map(int,input().split())
	edges = []
	for _ in range(E):
		edges.append(tuple(map(int,input().split())))
	must = list(map(int,input().split()))
	print(solution(V,E,edges,must))