1. 문제
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.
재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
선거구를 나누는 방법은 다음과 같다.
- 기준점 (x, y)와 경계의 길이 d1, d2를 정한다.
(d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N) - 다음 칸은 경계선이다.
- (x, y), (x+1, y-1), ..., (x+d1, y-d1)
- (x, y), (x+1, y+1), ..., (x+d2, y+d2)
- (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
- (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)
- 경계선과 경계선의 안에 포함되어있는 곳은 5번 선거구이다.
- 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
- 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
- 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
- 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
- 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.
구역 (r, c)의 인구는 A[r][c]이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.
제한 사항
시간 : 1 초
메모리 : 512 MB
5 ≤ N ≤ 20
1 ≤ A[r][c] ≤ 100
입력
첫째 줄에 재현시의 크기 N이 주어진다.
둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A[r][c]를 의미한다.
출력
첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.
- 키워드
- 일단 무식하게 풀면 답이 나온다. Bruteforce를 사용해보자.
2. 풀이
처음 이 문제를 봤을 때 이걸 어떻게 1초라는 시간안에 해결을 할 까 고민이 되었다.
방법이라고 해봐야 떠오르는 것은 5번 지역구가 나오는 모든 경우의 수를 돌려보는 Bruteforce뿐이고,
그 외에 다른 방법이 좀처럼 떠오르지도 않았다.
무엇보다 모양이 정사각형이 아닌 중구난방한 사각형이라 더더욱 로직이 떠오르질 않았다.
다른 사람들의 생각을 알아보기 위해 구글링을 돌려본 결과 정말 무식하게 풀어보는 것이 정답인 거 같다.
먼저 이 문제의 핵심은 모든 경우의 수 즉, 5번 지역구를 기준으로 값을 구하는 것이다.
5번 지역구의 경계선을
- (x, y), (x+1, y-1), ..., (x+d1, y-d1)
- (x, y), (x+1, y+1), ..., (x+d2, y+d2)
- (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
- (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)
이렇게 설명했지만, 처음 이 문제를 풀 때 머리에 과부하가 오는 것은 정상적일 것이다...
쉽게 말해서 x,y는 사각형에서 맨 꼭대기를 말하는 것이며,
d1,d2는 왼쪽 끝까지의 길이, 오른쪽 끝까지의 길이다.
즉 1번은 왼쪽 위, 2번은 오른쪽 위, 3번은 왼쪽 아래, 4번은 오른쪽 아래 경계선을 뜻한다.
다음 테스트케이스를 살펴보자.
8
1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 1
4 5 6 7 8 9 1 2
5 6 7 8 9 1 2 3
6 7 8 9 1 2 3 4
7 8 9 1 2 3 4 5
8 9 1 2 3 4 5 6
먼저, 우리가 탐색해야 할 부분은 (x,y)를 기준으로 해야하므로 이 부분만 탐색을 해주면 된다.
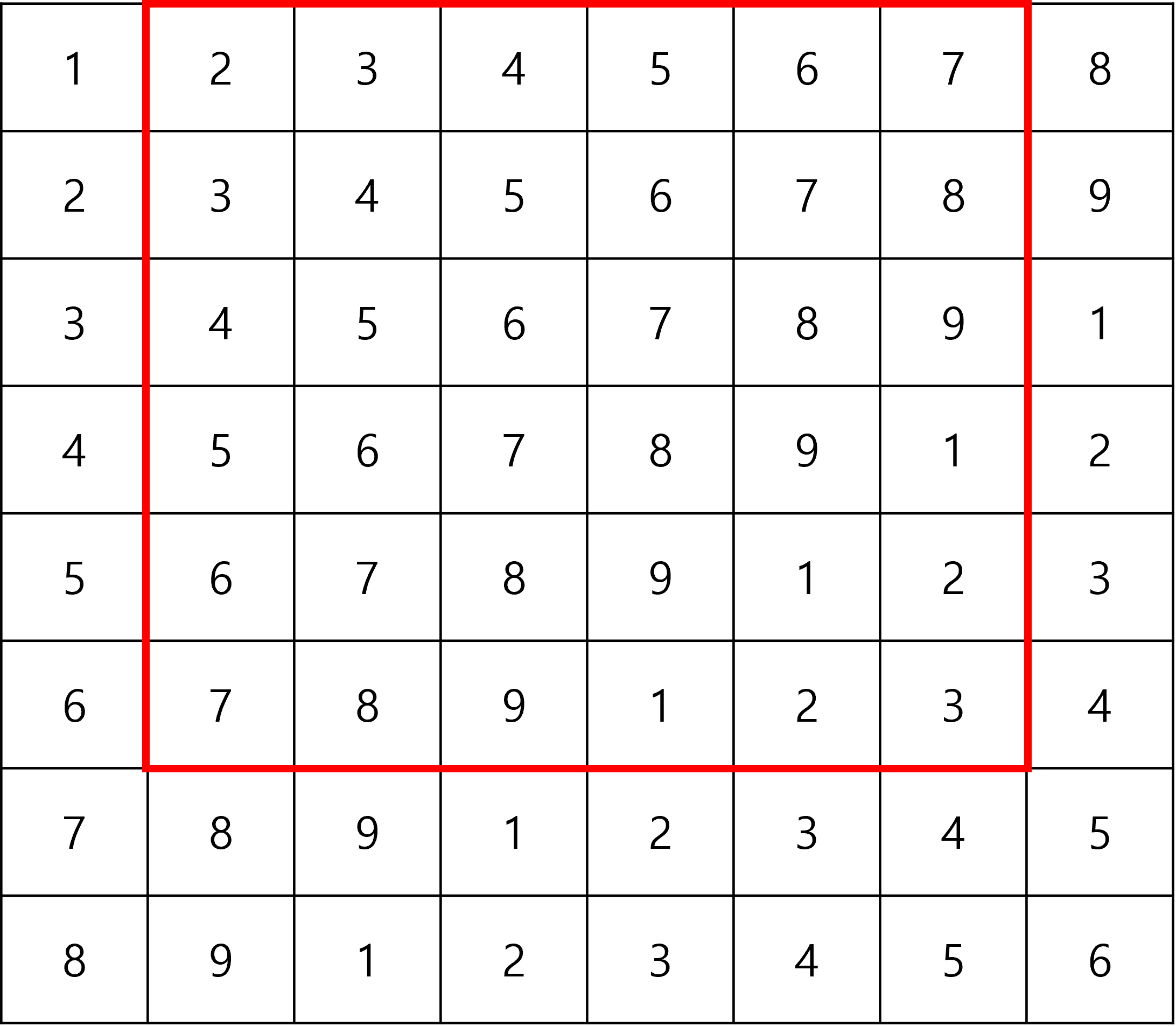
빨간 부분 안에서 특정 x,y를 기준으로 왼쪽 아래로 최대 길이까지 탐색한다.
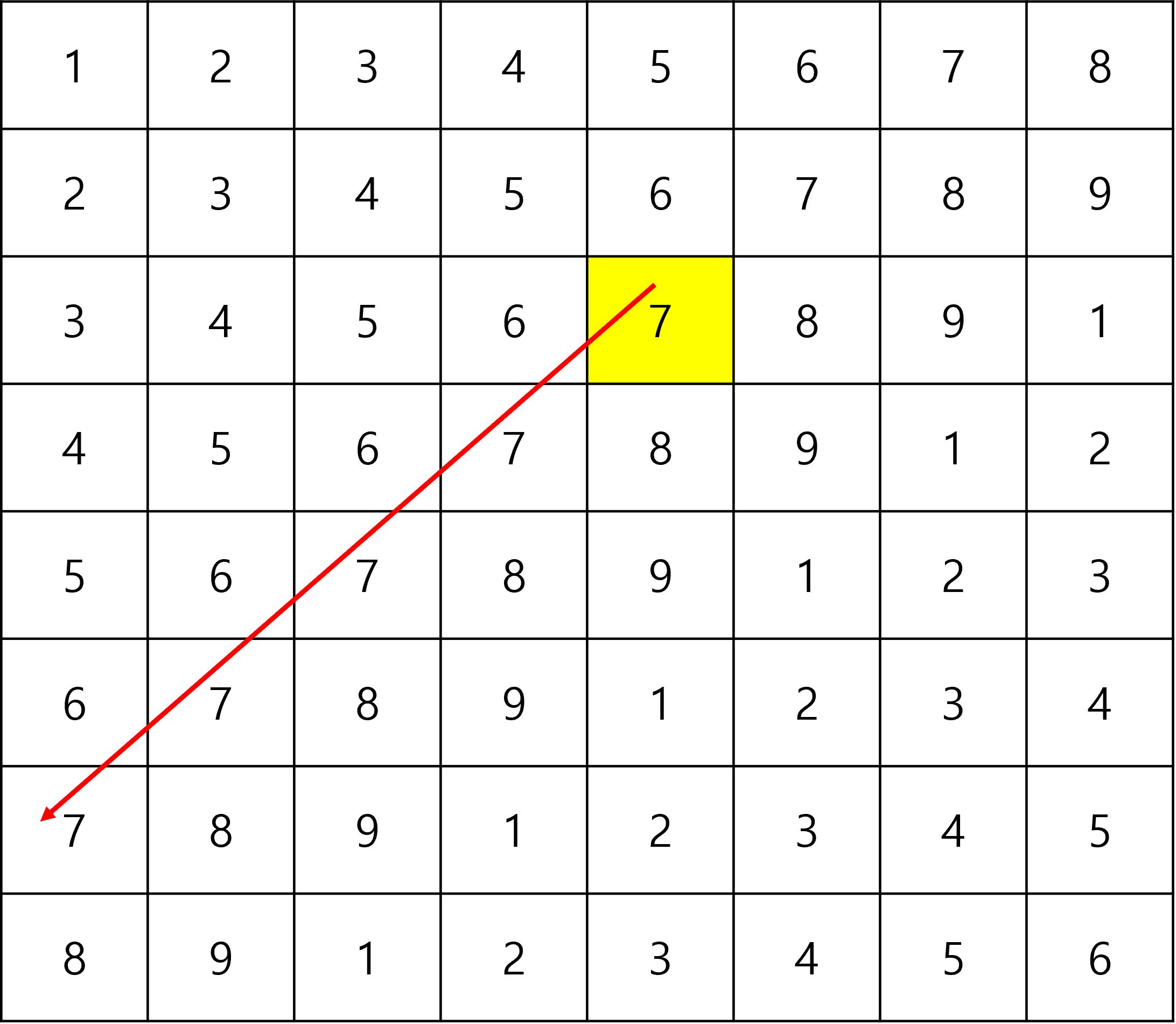
예시로 (3,5)를 해보자.
(3,5)에서 최대한 왼쪽 아래로 내려갈 수 있는지 체크하고
도착한 곳을 모두 저장한다.
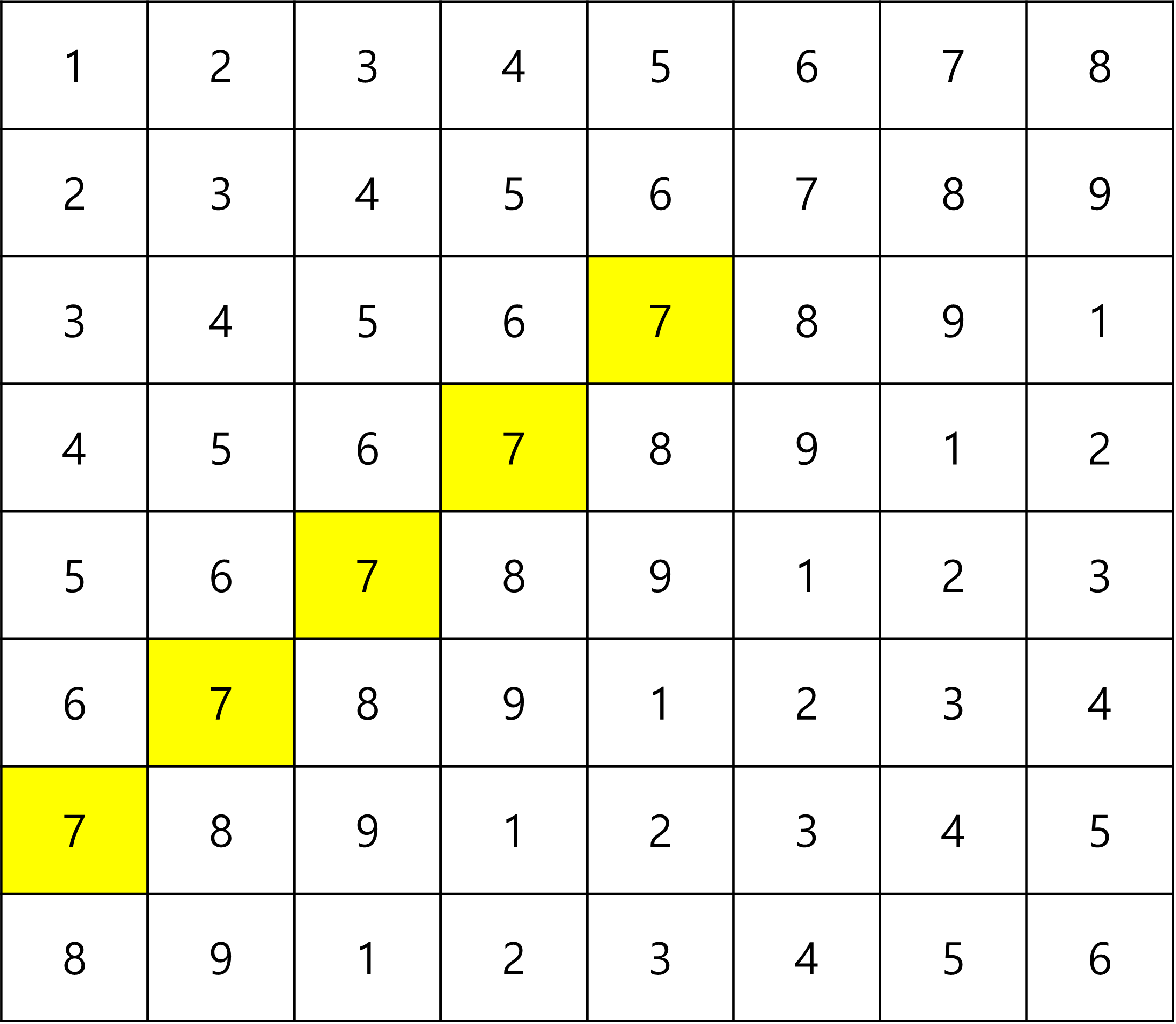
그리고 처음 시작한 곳 그리고 방문한 곳을 기준으로 오른쪽 아래로 탐색을 진행한다.
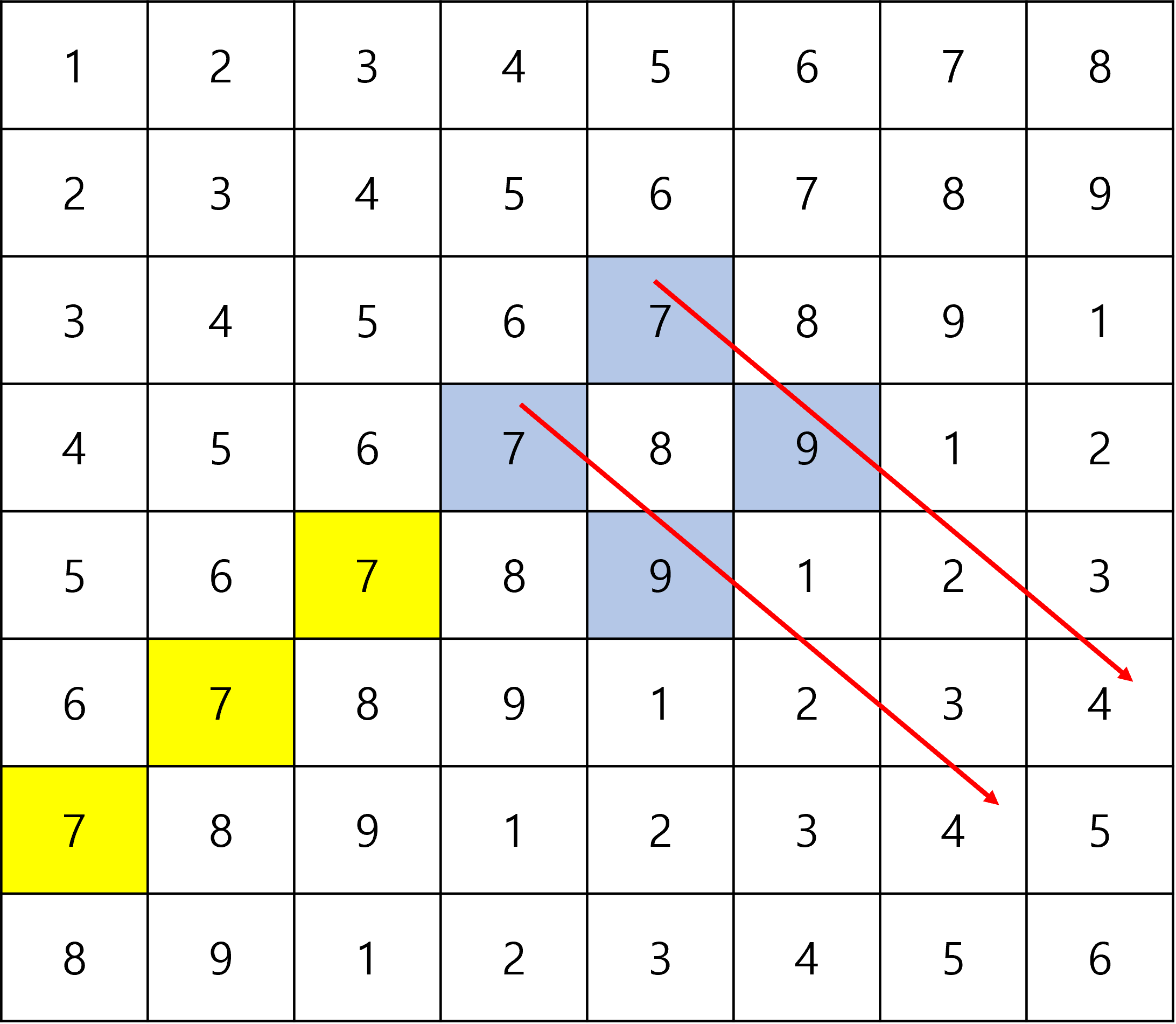
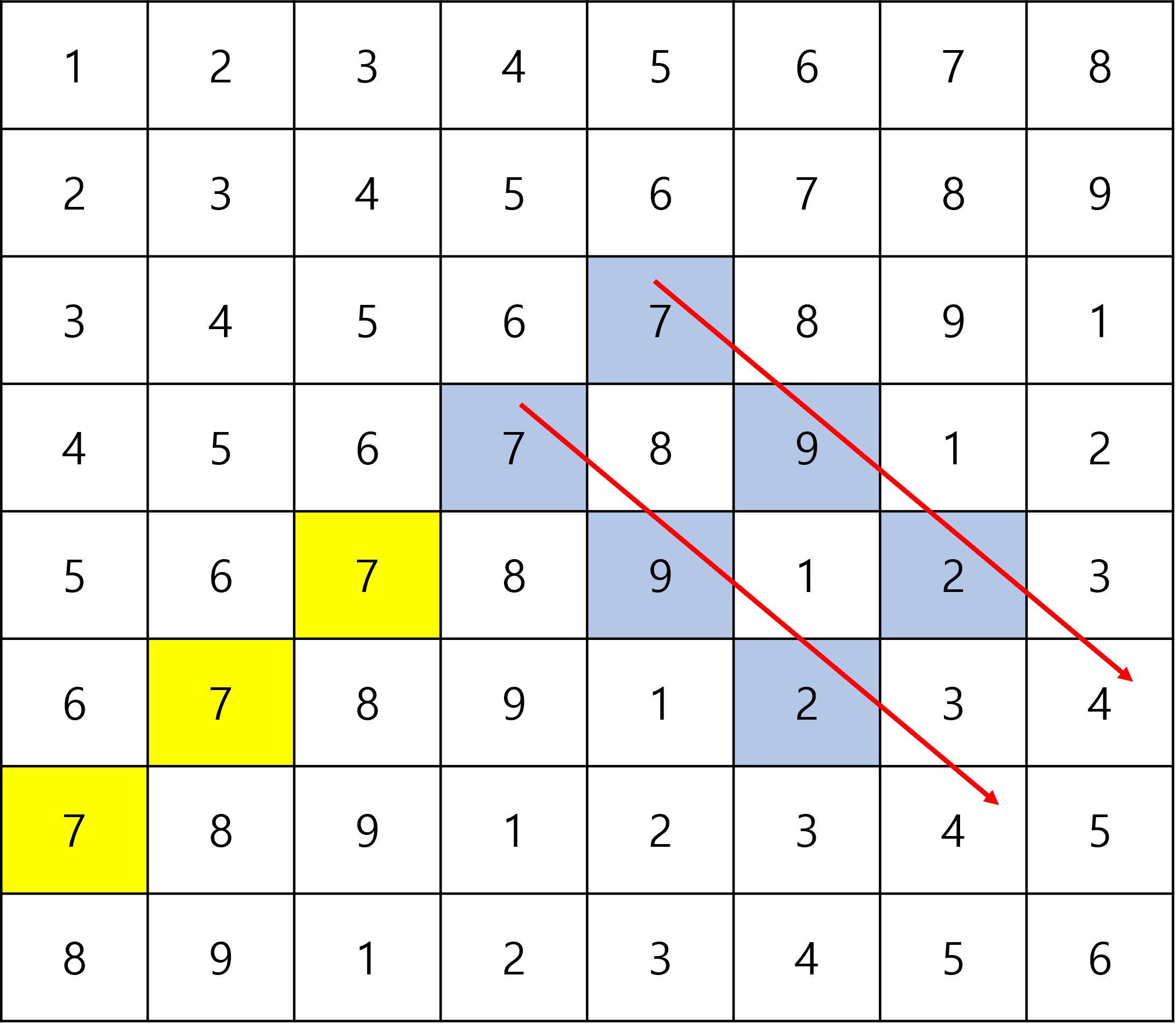
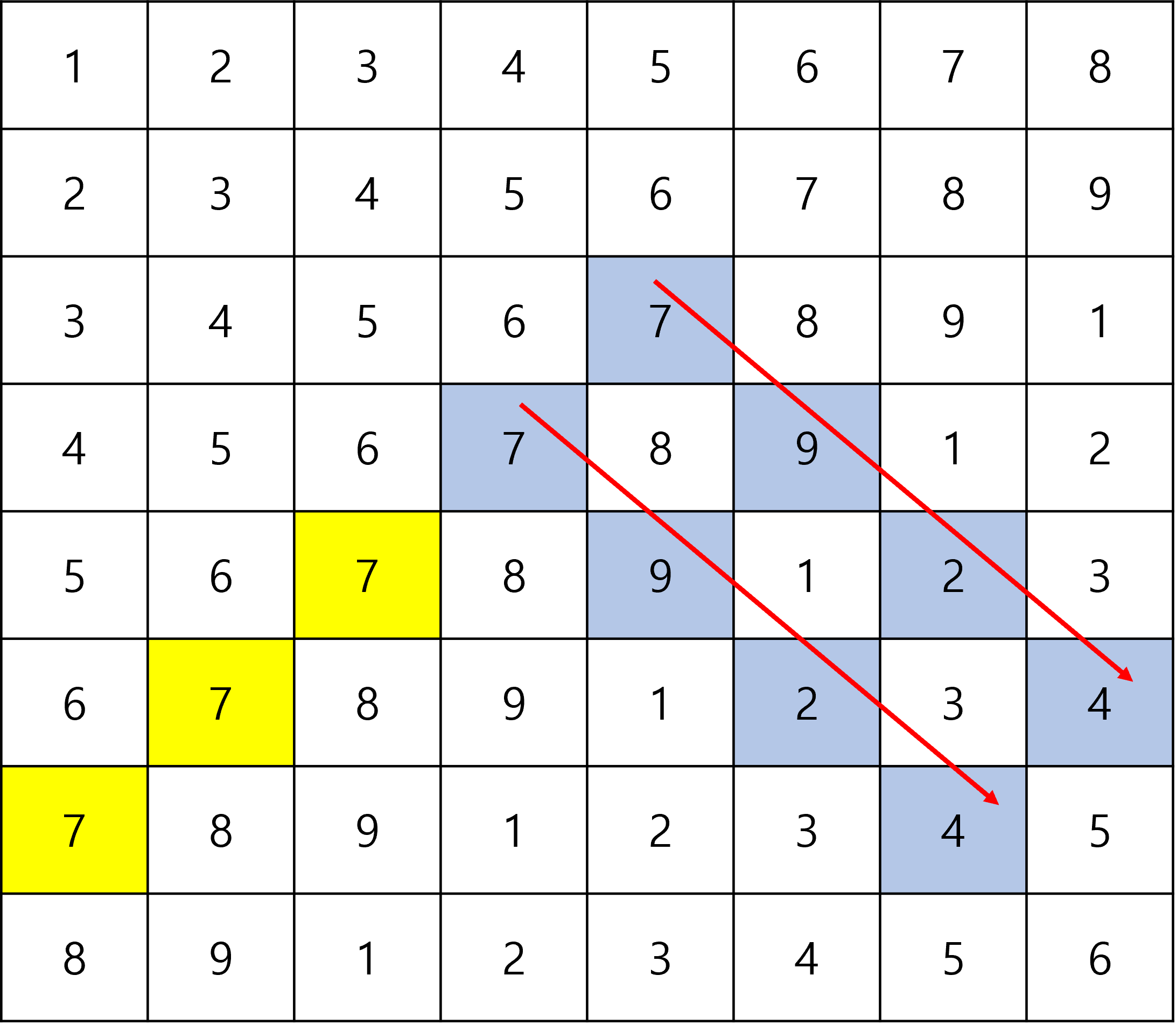
도착한 곳을 차례로 저장한다.
다른 곳도 똑같이 탐색하여 방문한 곳을 저장하도록 한다.
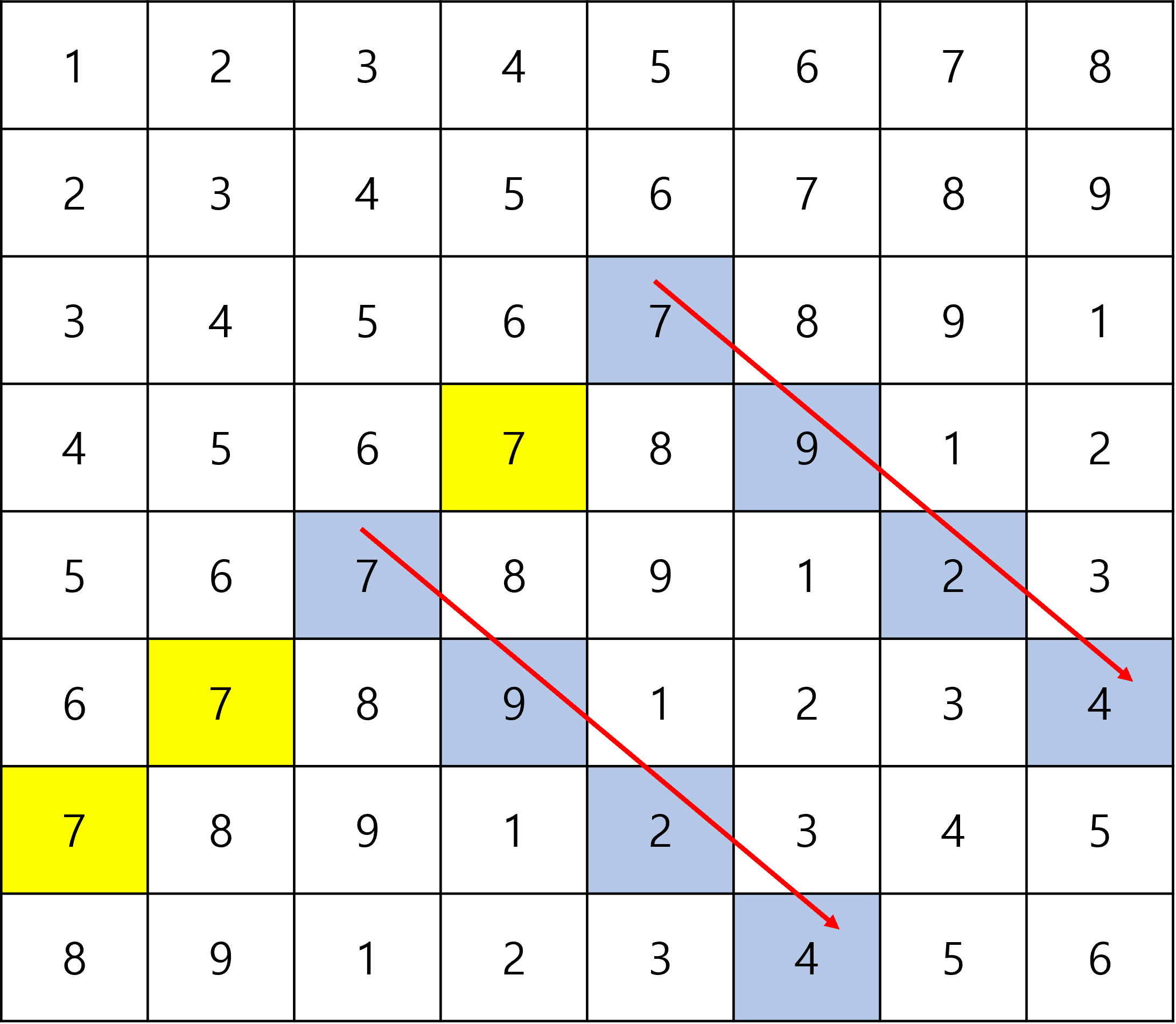
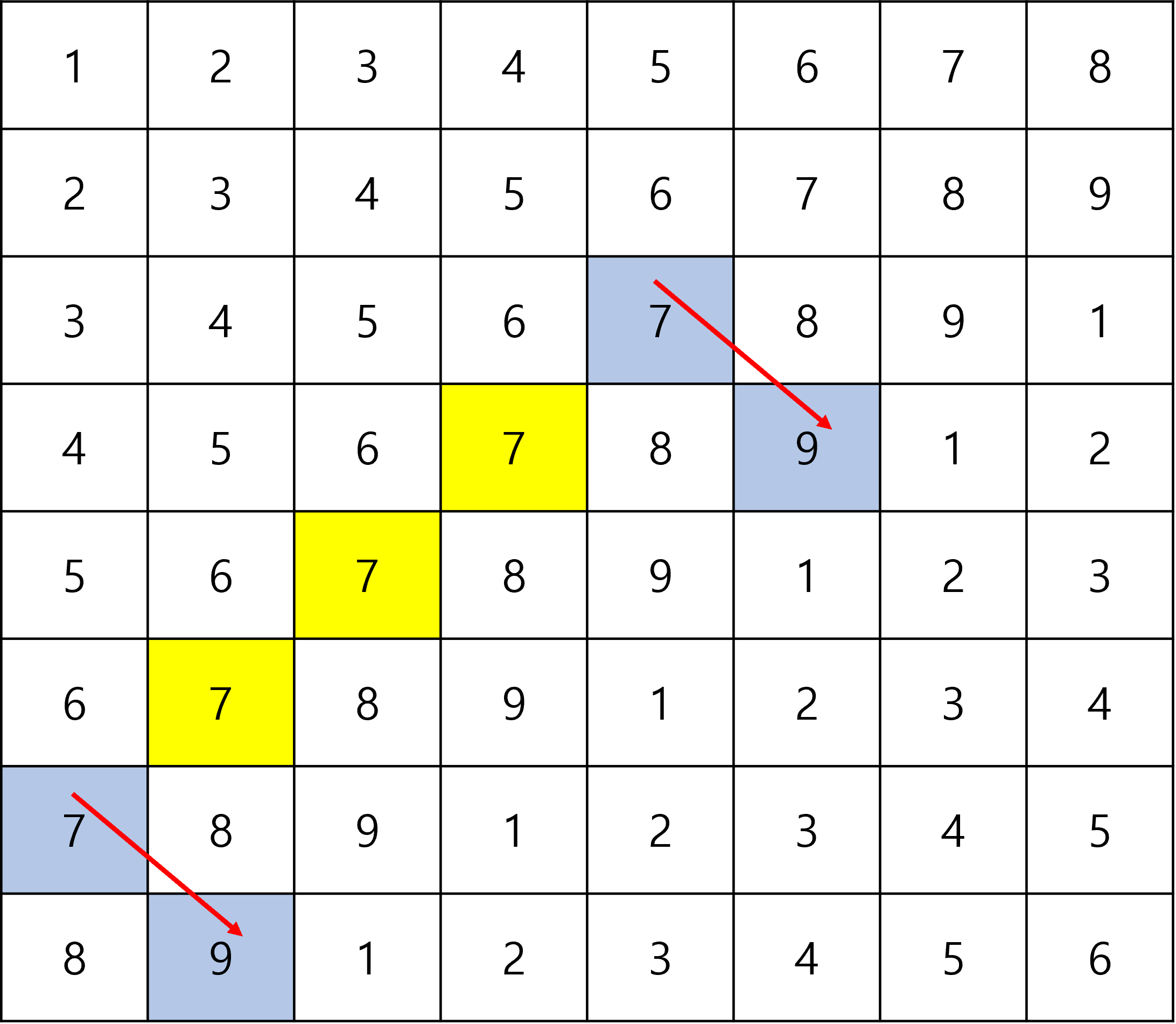
처음 빨간 영역에 해당됐던 부분을 기준으로 시작해서 모든 곳을 탐색 완료했다면
저장된 내용들을 기준으로 각 지역구 별로 인구 계산을 하도록 한다.
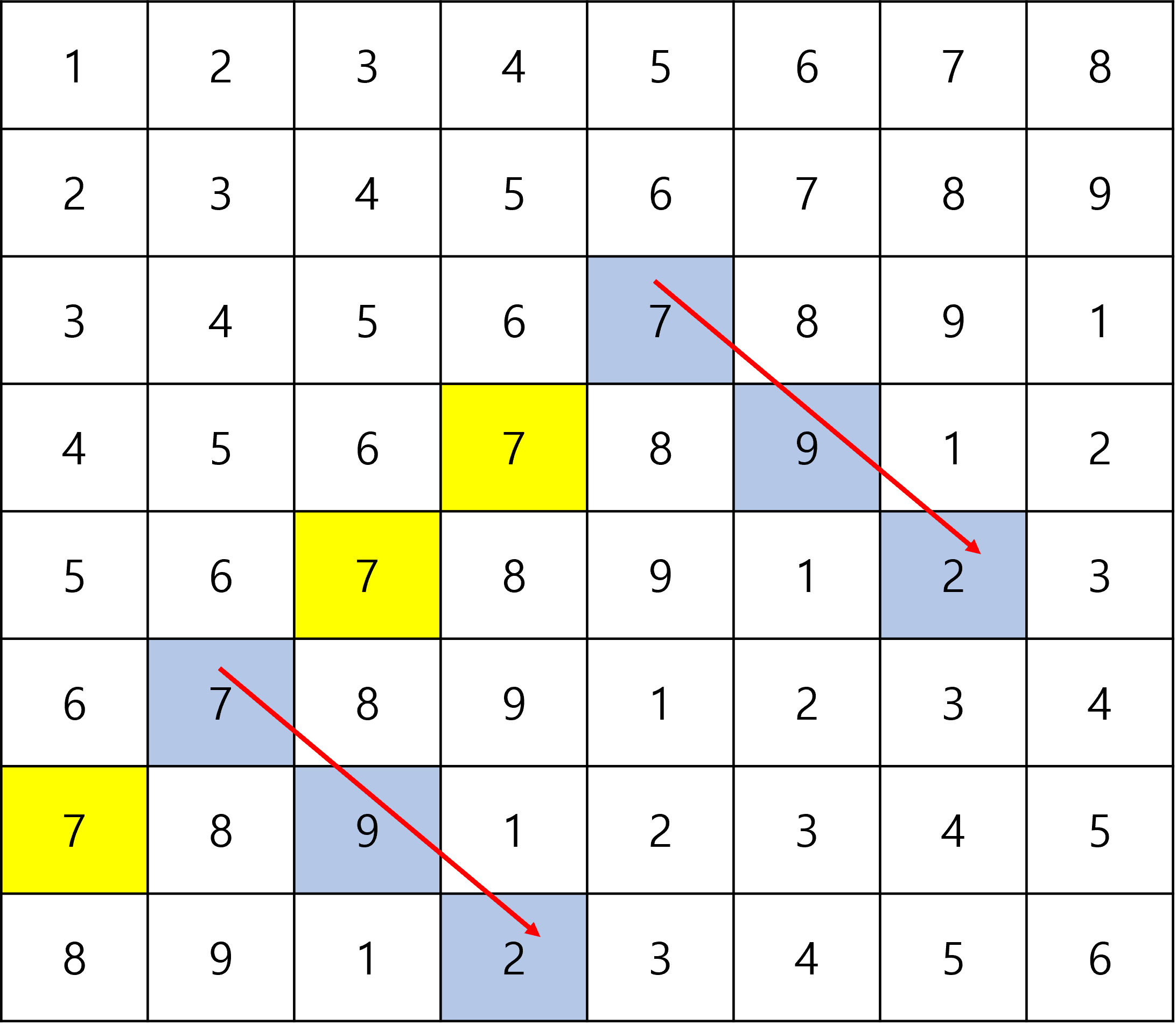
예를 들어, 지금 탐색했던 (3,5) 일부를 계산해보자.
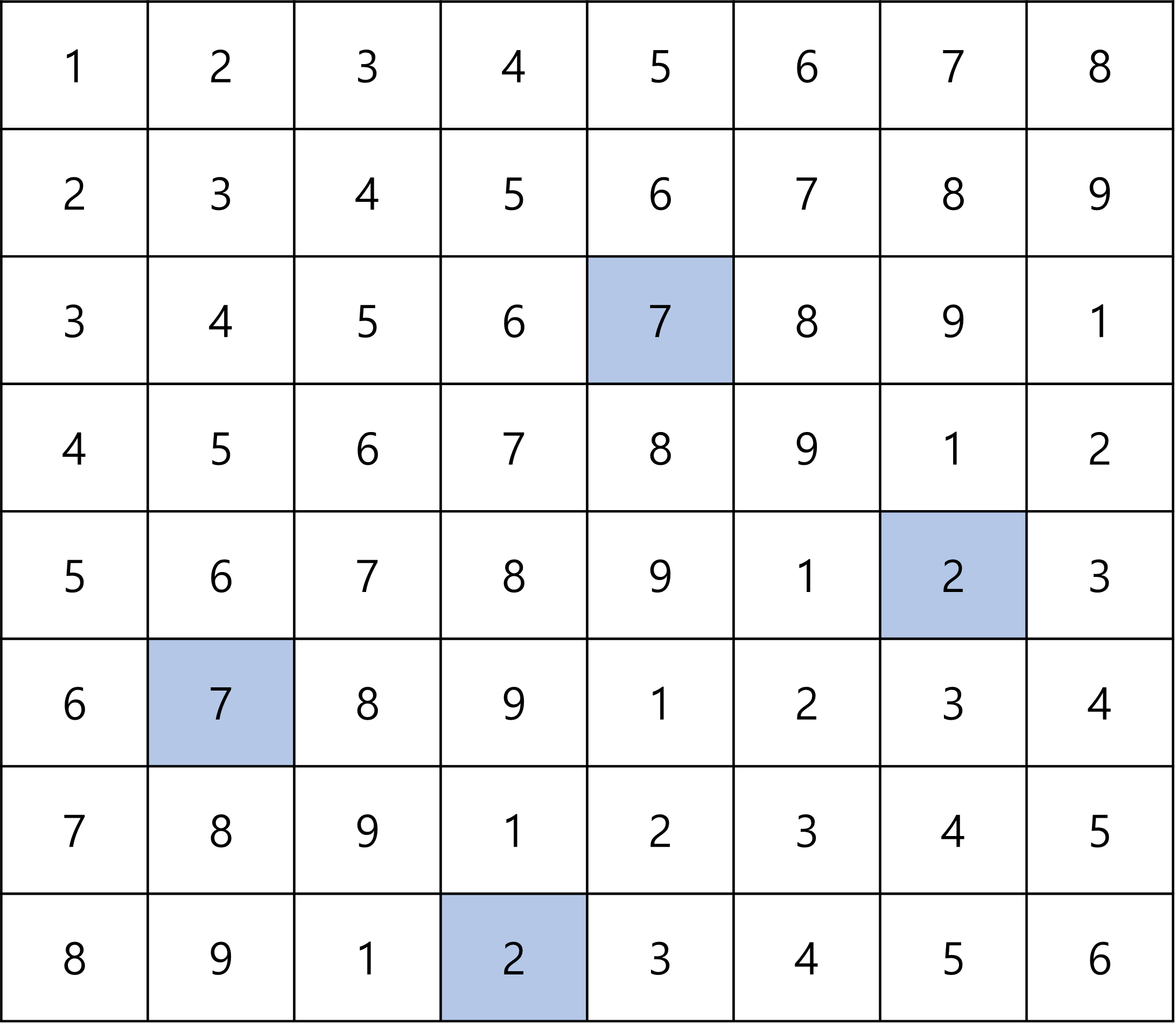
좀 전에 탐색하면서 저장한 경계선의 끝부분이다.
해당 부분을 기준으로 1,2,3,4 지역구의 인구를 계산한다.
계산 하기 전 전체 인구 수를 먼저 계산하고
그 다음 지역구 인구를 계산하도록 하자.
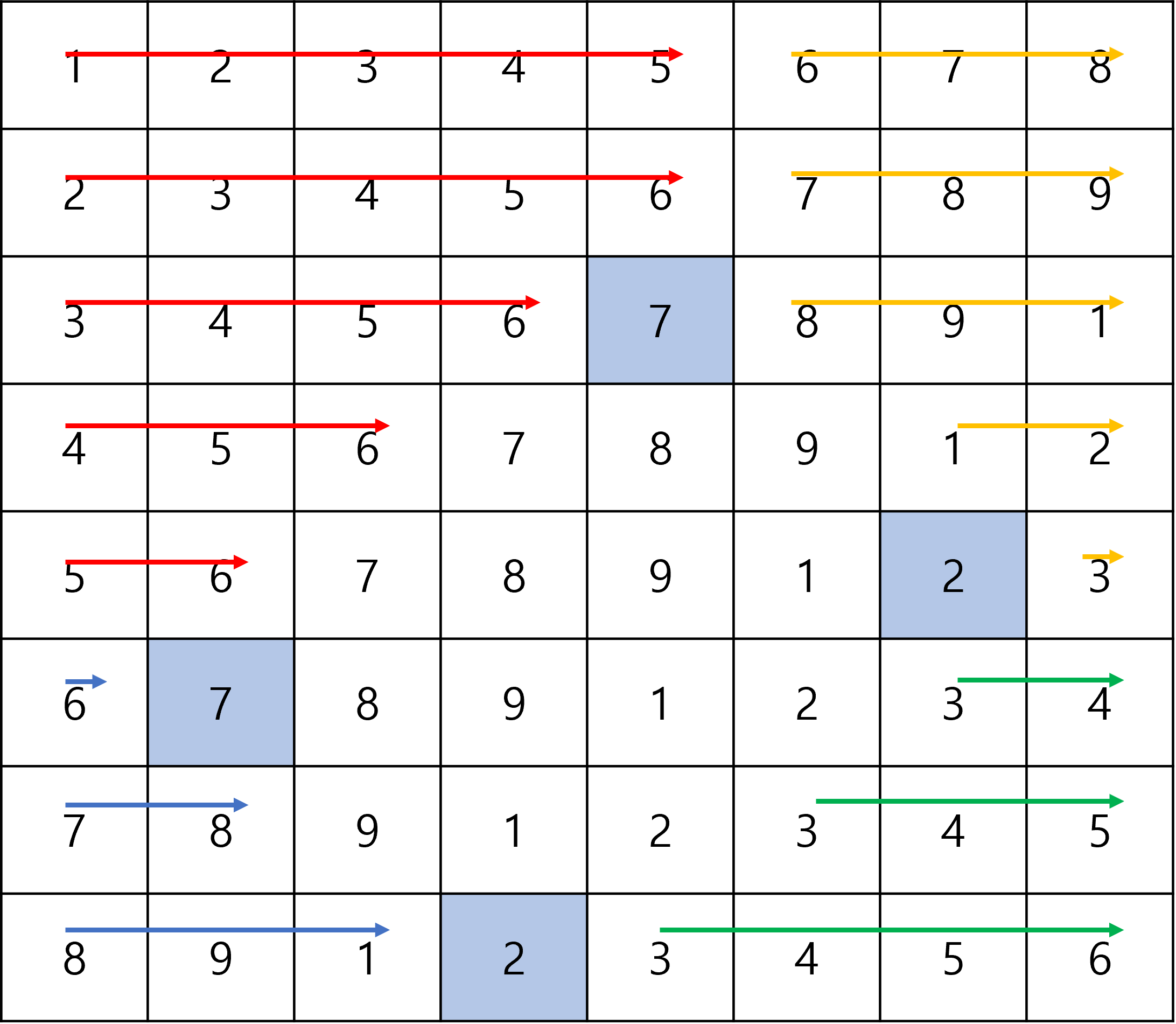
그리고 5번 지역구 인구를 계산해야 하는데
전체 인구 수 - (1번 지역구 + 2번 지역구 + 3번 지역구 + 4번 지역구)를 하면 쉽게 구할 수 있다
해당 과정을 나올 수 있는 모든 5번 지역구 경우의 수만큼 반복하면 된다. 정말 무식한 방법이다.
3. 소스코드
import sys
input = sys.stdin.readline
# 5번 지역구 구역 찾기
def find_divide(N,board,row,col):
half = [] # 위 그리고 왼쪽 점 저장
result = [] # 4점 저장
for d1 in range(1,N//2+1):
if 0 <= row+d1 < N and 0 <= col-d1 < N:
half.append([row+d1,col-d1])
else:
break
for d2 in range(1,N//2+1):
for i in half:
r,c = i
if 0 <= row+d2 < N and 0 <= col+d2 < N and 0 <= r+d2 < N and 0 <= c+d2 < N:
result.append([(row,col),(r,c),(row+d2,col+d2),(r+d2,c+d2)])
else:
break
return result
def city1(N,board,u,l): # 왼쪽 위 지역구 계산
people = 0
end = u[1]
for row in range(l[0]):
if row >= u[0]:
end -= 1
for col in range(end+1):
people += board[row][col]
return people
def city2(N,board,u,r): # 오른쪽 위 지역구 계산
people = 0
start = u[1]+1
for row in range(r[0]+1):
if row > u[0]:
start += 1
for col in range(start,N):
people += board[row][col]
return people
def city3(N,board,d,r): # 오른쪽 아래 지역구 계산
people = 0
start = r[1]
for row in range(r[0]+1,N):
for col in range(start,N):
people += board[row][col]
if start != d[1]:
start -= 1
return people
def city4(N,board,d,l): # 왼쪽 아래 지역구 계산
people = 0
end = l[1]
for row in range(l[0],N):
for col in range(end):
people += board[row][col]
if end < d[1]:
end += 1
return people
def solution(N,board):
divide = []
for row in range(N):
for col in range(1,N):
divide += find_divide(N,board,row,col)
people = 0
for i in board:
people += sum(i)
answer = people
for i in divide:
u,l,r,d = i
max_p,min_p = 0,1e9 # 최대 인구수와 최소 인구수
p1 = city1(N,board,u,l)
max_p = max(p1,max_p)
min_p = min(p1,min_p)
p2 = city2(N,board,u,r)
max_p = max(p2,max_p)
min_p = min(p2,min_p)
p3 = city3(N,board,d,r)
max_p = max(p3,max_p)
min_p = min(p3,min_p)
p4 = city4(N,board,d,l)
max_p = max(p4,max_p)
min_p = min(p4,min_p)
p5 = people - (p1+p2+p3+p4)
max_p = max(p5,max_p)
min_p = min(p5,min_p)
answer = min(answer,max_p-min_p)
return answer
if __name__ == "__main__":
N = int(input())
board = []
for _ in range(N):
board.append(list(map(int,input().split())))
print(solution(N,board))4. 후기
테스트 출력을 지우지 않아 한 번 오답판정을 받았지만 해당 과정은 여유롭게 수행하는 거 같다.
Bruteforce를 웬만하면 사용하지 않으려 했지만, 표본이 작아서 일단 풀고보자라고 생각했던 거 같다.
실제로 이렇게 기업 코딩테스트에서 나오진 않겠지만, 가끔은 무식하게 풀어보자는 것을
고려해볼 필요는 있을 거같다. 제발 이렇게 나오지만 않았으면 한다.
