[백준 17837번] 새로운 게임 2

mokomoko·2022년 2월 21일

1. 문제

재현이는 주변을 살펴보던 중 체스판과 말을 이용해서 새로운 게임을 만들기로 했다. 새로운 게임은 크기가 N×N인 체스판에서 진행되고, 사용하는 말의 개수는 K개이다. 말은 원판모양이고, 하나의 말 위에 다른 말을 올릴 수 있다. 체스판의 각 칸은 흰색, 빨간색, 파란색 중 하나로 색칠되어있다.

게임은 체스판 위에 말 K개를 놓고 시작한다. 말은 1번부터 K번까지 번호가 매겨져 있고, 이동 방향도 미리 정해져 있다. 이동 방향은 위, 아래, 왼쪽, 오른쪽 4가지 중 하나이다.

턴 한 번은 1번 말부터 K번 말까지 순서대로 이동시키는 것이다. 한 말이 이동할 때 위에 올려져 있는 말도 함께 이동한다. 말의 이동 방향에 있는 칸에 따라서 말의 이동이 다르며 아래와 같다. 턴이 진행되던 중에 말이 4개 이상 쌓이는 순간 게임이 종료된다.

A번 말이 이동하려는 칸이
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
  - A번 말의 위에 다른 말이 있는 경우에는 A번 말과 위에 있는 모든 말이 이동한다.
  - 예를 들어, A, B, C로 쌓여있고, 이동하려는 칸에 D, E가 있는 경우에는 A번 말이 이동한 후에는 D, E, A, B, C가 된다.
- 빨간색인 경우에는 이동한 후에 A번 말과 그 위에 있는 모든 말의 쌓여있는 순서를 반대로 바꾼다.
  - A, B, C가 이동하고, 이동하려는 칸에 말이 없는 경우에는 C, B, A가 된다.
  - A, D, F, G가 이동하고, 이동하려는 칸에 말이 E, C, B로 있는 경우에는 E, C, B, G, F, D, A가 된다.
- 파란색인 경우에는 A번 말의 이동 방향을 반대로 하고 한 칸 이동한다. 방향을 반대로 바꾼 후에 이동하려는 칸이 파란색인 경우에는 이동하지 않고 가만히 있는다.
- 체스판을 벗어나는 경우에는 파란색과 같은 경우이다.

다음은 크기가 4×4인 체스판 위에 말이 4개 있는 경우이다.

첫 번째 턴은 다음과 같이 진행된다.

두 번째 턴은 다음과 같이 진행된다.

체스판의 크기와 말의 위치, 이동 방향이 모두 주어졌을 때, 게임이 종료되는 턴의 번호를 구해보자.

제한 사항

시간 : 0.5 초
메모리 : 512 MB
4 ≤ N ≤ 12
4 ≤ K ≤ 10

입력

첫째 줄에 체스판의 크기 N, 말의 개수 K가 주어진다. 둘째 줄부터 N개의 줄에 체스판의 정보가 주어진다. 체스판의 정보는 정수로 이루어져 있고, 각 정수는 칸의 색을 의미한다. 0은 흰색, 1은 빨간색, 2는 파란색이다.

다음 K개의 줄에 말의 정보가 1번 말부터 순서대로 주어진다. 말의 정보는 세 개의 정수로 이루어져 있고, 순서대로 행, 열의 번호, 이동 방향이다. 행과 열의 번호는 1부터 시작하고, 이동 방향은 4보다 작거나 같은 자연수이고 1부터 순서대로 →, ←, ↑, ↓의 의미를 갖는다.

같은 칸에 말이 두 개 이상 있는 경우는 입력으로 주어지지 않는다.

출력

게임이 종료되는 턴의 번호를 출력한다. 그 값이 1,000보다 크거나 절대로 게임이 종료되지 않는 경우에는 -1을 출력한다.

- 키워드

간단하게 말하면 3차원 배열을 사용, 편하게 구현하기 위해선 N*N 칸 별로 Deque를 하나씩 두자.

각 역할군 별로 설계를 제대로 하지 않으면 머리에 과부하가 올 확률이 높다. 잘 생각해두자.

2. 풀이

문제를 봤을 땐 직관적이긴 하지만, 햇갈릴 수 밖에 없는 문제같다.

이 문제를 풀면서 햇갈리지 않으려면 문제를 제대로 읽고 이해한 뒤 풀어야 만 한다.

문제를 다시보자.

먼저, 특정 말이 이동하는데 흰색 칸, 빨간 칸, 파란 칸 세 가지 경우의 수로 나뉜다.

흰색 칸의 경우 이동하려는 칸에 말이 존재 할 경우 그 위에 올려놓는다.

그냥 이동하기만 하면 되는 이동 후 저장만 생각하면 된다.
빨간 칸의 경우 이동하려는 칸에 말이 존재 할 경우 그 위에 올려놓는다.

그리고 그 올려놓은 말까지만 순서를 뒤집는다.
파란 칸의 경우 이동하지 않고 이동하려는 말의 번호의 방향만 바꾼다.

그리고, 다시 체크한다.
1. 흰색 칸의 경우 이동하려는 칸에 말이 존재 할 경우 그 위에 올려놓는다.
2. 빨간 칸의 경우 이동하려는 칸에 말이 존재 할 경우 그 위에 올려놓는다.
  그리고 그 올려놓은 말까지만 순서를 뒤집는다.
3. 파란 칸의 경우 움직이지 않는다.

여기서 우리가 만들어야 할 기능은 다음과 같다.

특정 말의 집단을 이동하는 기능
특정 말의 기준을 토대로 뒤집는 기능
특정 한 가지 말의 방향을 뒤집는 기능

이 세 가지만 잘 구현한다면 문제를 해결할 수 있다.

입력할 때 N*N의 체스판을 입력한다.

예시로, 테스트 케이스 5번을 보자.

6 10
0 1 2 0 1 1
1 2 0 1 1 0
2 1 0 1 1 0
1 0 1 1 0 2
2 0 1 2 0 1
0 2 1 0 2 1
1 1 1
2 2 2
3 3 4
4 4 1
5 5 3
6 6 2
1 6 3
6 1 2
2 4 3
4 2 1

해당 테스트 케이스를 입력하면 다음과 같은 체스판이 나올 것이다.

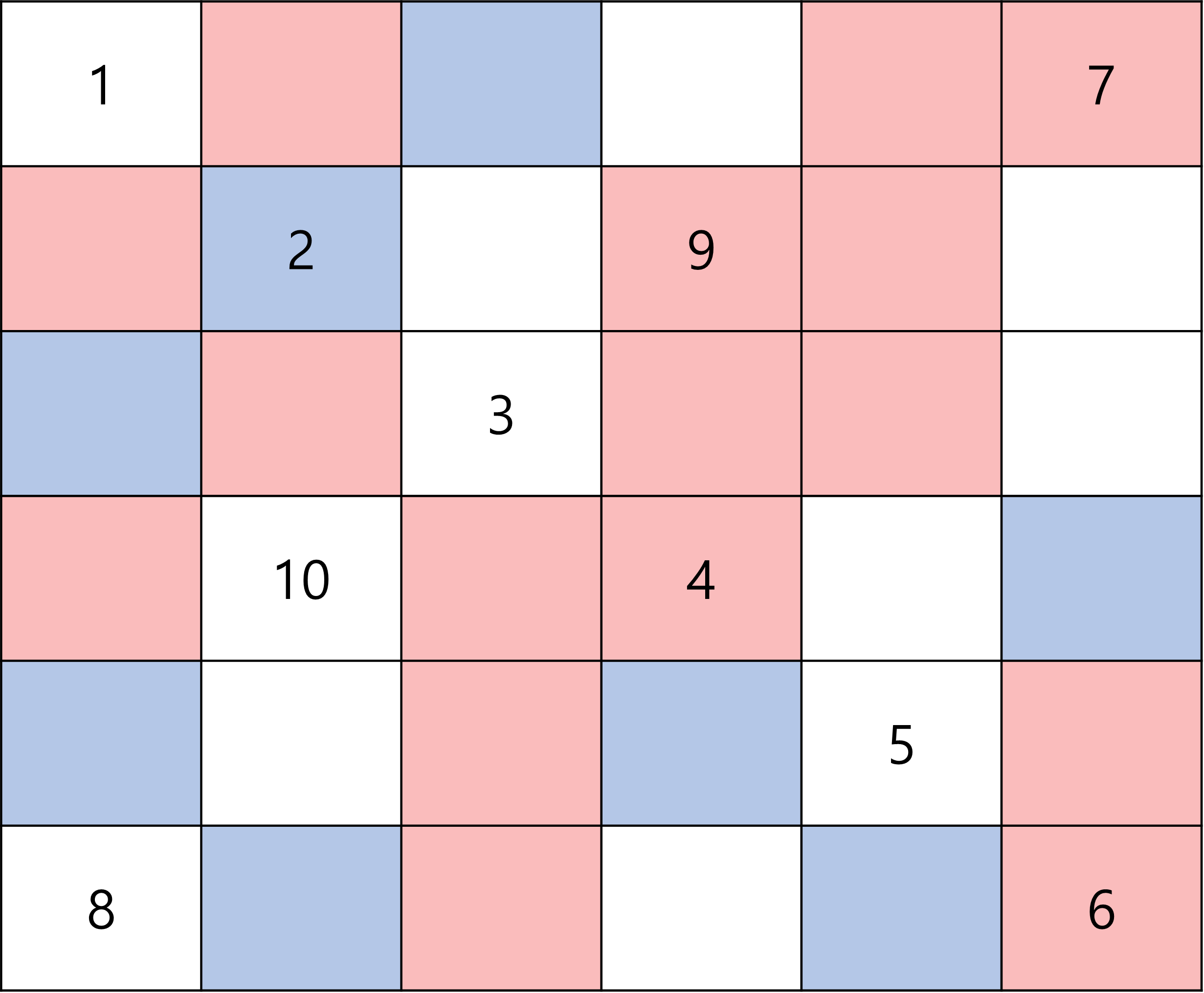
입력 자체는 이렇게 받지만, 기능을 구현할 때 우리는 고려해야 할 사항이 있다.

체스판을 벗어나는 경우에는 파란색과 같은 경우이다.

그러므로, (N+2) * (N+2) 로 설정하여 문제를 풀면 훨씬 수월하게 풀 수 있다.

각 테두리 부분을 파란색으로 설정해서 다시 받는다.

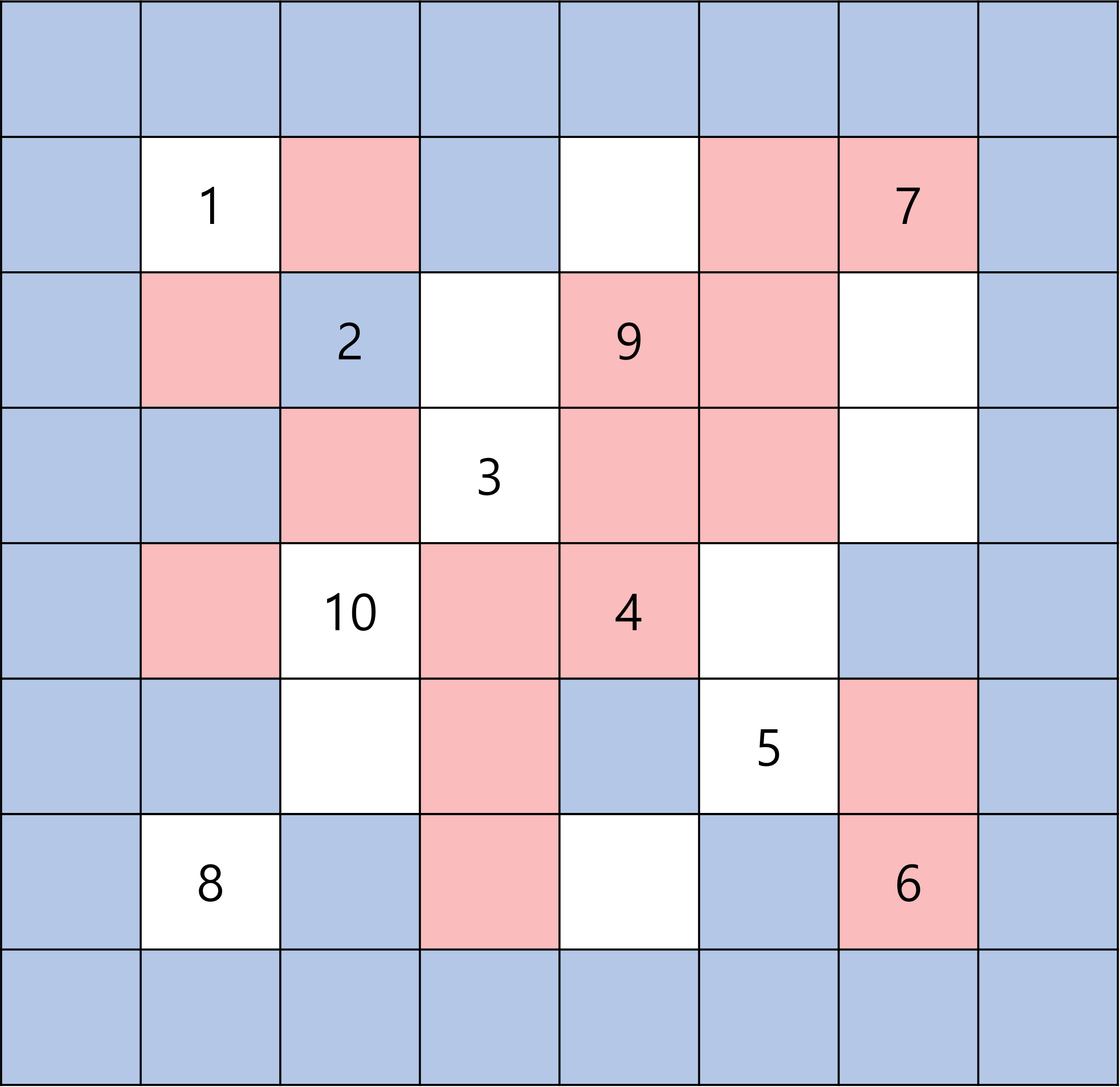
이제 이동하는 로직을 만들어야 한다.

1. 특정 말의 집단을 이동하는 기능

현재 위치에 있는 특정 말을 포함하여 그 위에 있는 말들을 이동할 칸에 이동시킨다.

이동할 위치에 말이 존재할 경우 그 위에 올려놓는다.

Queue를 써도 되지만, Deque를 사용하기가 편하다.

다음 과정을 거친다.

이동 집단 Deque를 생성하고, 현재 위치의 말의 가장 앞에 있는 말을 넣는다.
Deque의 끝 부분이 특정 말의 번호일 때 까지 현재 위치의 말을 계속 넣는다.
이동할 위치의 앞에 Deque의 끝 부분부터 차례대로 넣는다.

def move(board_q,row,col,w,i):
	move_q = deque()
	move_q.append(board_q[row][col].popleft())

	while move_q[-1] != i:
		move_q.append(board_q[row][col].popleft())

	while move_q:
		board_q[row+w[0]][col+w[1]].appendleft(move_q.pop())

이동은 흰색이든 빨간색이든 이 함수만 사용한다.

이동을 한 뒤 이동한 칸의 위치를 저장한다.

def save(units,board_q,row,col):
	for i in board_q[row][col]:
		units[i-1][0] = row
		units[i-1][1] = col

2. 특정 말의 집단을 뒤집는 기능

move 함수 안에 조건을 설정해 구현해도 되지만, 나는 따로 구현했다.

빨간 칸에 도달했을 경우 흰색 칸 과정을 거친 뒤 해당 기능을 수행한다.

뒤집을 Deque를 생성하고 해당 칸의 가장 앞 부분을 넣는다.
Deque의 마지막 부분이 특정 말의 번호일 때 까지 넣는다.
이동한 위치에 Deque의 앞 부분부터 차례대로 넣는다.

def reverse(board_q,row,col,i):
	reverse_q = deque()
	reverse_q.append(board_q[row][col].popleft())

	while reverse_q[-1] != i:
		reverse_q.append(board_q[row][col].popleft())

	while reverse_q:
		board_q[row][col].appendleft(reverse_q.popleft())

해당 기능은 빨간 칸에 도달했을 때만 사용하고, 위치가 변경되지 않으므로

save를 실행할 이유가 없다.

3. 특정 한 가지 말의 방향을 뒤집는 기능

해당 기능은 따로 만들 필요는 없다. 다만, 해당 기능을 수행 한 뒤

다시 1,2 과정을 거치는지의 여부를 판단해야 한다.

# 1 : right, 2 : left, 3 : up, 4 : down
way = [(0,0),(0,1),(0,-1),(-1,0),(1,0)]
if units[i][2] % 2 == 0:
	units[i][2] -= 1
else:
	units[i][2] += 1

이 과정을 거치고 다시 이동할 칸의 색을 판별한다.

흰색 칸의 경우 move->save

빨간 칸의 경우 move->save->reverse를 하면된다.

정리

이동할 칸이

흰색 칸의 경우 move를 하고 save한다.
빨간 칸의 경우 move를 하고 save한 뒤, reverse한다.
파란 칸의 경우 방향을 바꾸고 다시
- 흰색 칸의 경우 move를 하고 save한다.
- 빨간 칸의 경우 move를 하고 save한 뒤, reverse한다.
- 파란 칸의 경우 아무 일도 일어나지 않는다.

3. 소스코드

import sys
from collections import deque
input = sys.stdin.readline

# 1 : right, 2 : left, 3 : up, 4 : down
way = [(0,0),(0,1),(0,-1),(-1,0),(1,0)]

def move(board_q,row,col,w,i):
	move_q = deque()
	move_q.append(board_q[row][col].popleft())

	while move_q[-1] != i:
		move_q.append(board_q[row][col].popleft())

	while move_q:
		board_q[row+w[0]][col+w[1]].appendleft(move_q.pop())	

def save(units,board_q,row,col):
	for i in board_q[row][col]:
		units[i-1][0] = row
		units[i-1][1] = col

def reverse(board_q,row,col,i):
	reverse_q = deque()
	reverse_q.append(board_q[row][col].popleft())

	while reverse_q[-1] != i:
		reverse_q.append(board_q[row][col].popleft())

	while reverse_q:
		board_q[row][col].appendleft(reverse_q.popleft())

def solution(N,K,board,units):
	board_q = [[deque() for _ in range(N+2)] for _ in range(N+2)] 
	for i in range(len(units)):
		row,col,w = units[i]
		board_q[row][col].append(i+1)
	cnt = 0
	while cnt <= 1000:
		cnt += 1
		for i in range(len(units)):
			row,col,w = units[i]
			if len(board_q[row][col]) >= 4:
				return cnt
			w = way[w]
			if board[row+w[0]][col+w[1]] == 0:
				move(board_q,row,col,w,i+1)
				save(units,board_q,row+w[0],col+w[1])
			elif board[row+w[0]][col+w[1]] == 1:
				move(board_q,row,col,w,i+1)
				reverse(board_q,row+w[0],col+w[1],i+1)
				save(units,board_q,row+w[0],col+w[1])
			else:
				if units[i][2] % 2 == 0:
					units[i][2] -= 1
				else:
					units[i][2] += 1
				row,col,w = units[i]
				w = way[w]
				if board[row+w[0]][col+w[1]] == 0:
					move(board_q,row,col,w,i+1)
					save(units,board_q,row+w[0],col+w[1])
				elif board[row+w[0]][col+w[1]] == 1:
					move(board_q,row,col,w,i+1)
					reverse(board_q,row+w[0],col+w[1],i+1)
					save(units,board_q,row+w[0],col+w[1])
			if len(board_q[units[i][0]][units[i][1]]) >= 4:
				return cnt 
	return -1

if __name__ == "__main__":
	N,K = map(int,input().split())
	board = [[2]*(N+2)]
	for _ in range(N):
		line = list(map(int,input().split()))
		board.append([2]+line+[2])
	board.append([2]*(N+2))
	units = []
	for i in range(K):
		units.append(list(map(int,input().split())))
	print(solution(N,K,board,units))