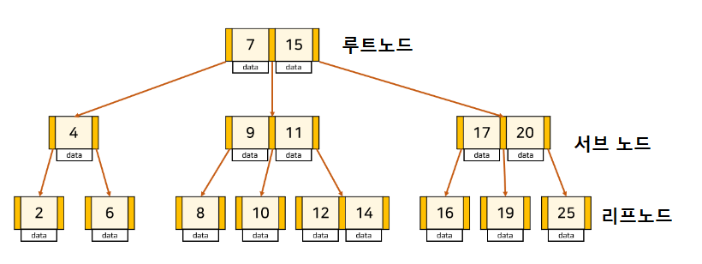
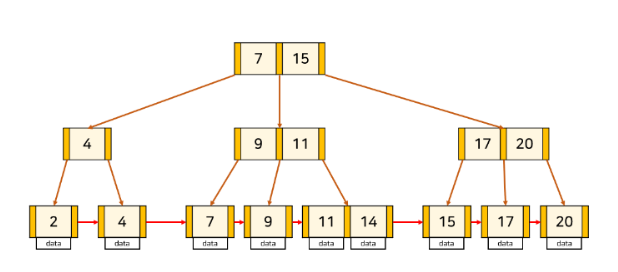
클러스터형 인덱스와 보조 인덱스는 모두 내부적으로 B-Tree(균형 트리)로 만들어진다.
🌲 B-Tree 인덱스
DB 인덱스 알고리즘 가운데 가장 일반적이며, 가장 먼저 도입되었다.
가장 범용적으로 사용되는 인덱스 알고리즘이다.
B는 Balanced를 의미한다.
칼럼의 원래 값을 변형시키지 않고,
인덱스 구조체 내에서 항상 정렬된 상태로 유지한다.
🎇 B-Tree 구조 및 특성
- 트리 구조의 최상위에 하나의 Root node가 존재
- 가장 하위에 있는 노드는 Leaf node
- 중간의 노드는 Branch node
- DB에서 인덱스와 실제 데이터는 따로 관리되는데, 인덱스의 Leaf node는 항상 실제 데이터 레코드를 찾아가기 위한
주소값을 가짐 - 노드는 MySQL에서는 페이지로, 최소한의 저장 단위(16KB)
- 무조건 Root node (Root page)부터 검색한다.
🎇 B-Tree 인덱스 키 추가, 삭제, 변경, 검색
INSERT
- 저장될 키 값을 사용해 B-Tree상의 적절 위치를 검색
- 저장 위치 결정하면 레코드의 키 값과 대상 레코드의 주소 정보를 B-Tree Leaf node에 저장
- Leaf node가 꽉차서 저장할 수 없으면 Leaf node split해야함 (
페이지 분할 작업으로 인해 추가 작업이 비용이 많이 듬)
DELETE
해당 키 값이 저장된 B-Tree의 Leaf node를 찾아 삭제 마크 작업
UPDATE
Leaf node의 위치때문에 단순히 키 값만 변경하는 것은 불가능
따라서 먼저 키 값을 삭제한 후 다시 새로운 키 값을 추가
SEARCH
- B-Tree의 Root node -> Branch node -> Leaf node까지 이동하며 비교 작업을 수행 (
트리 탐색과정) - 100% 일치 혹은 값의 앞부분만 일치하는 경우에 사용할 수 있음
- 인덱스의 키 값에 변형이 가해지면 B-Tree의 빠른 검색을 사용할 수 없음 -> 함수나 연산을 수행한 결과로 정렬하거나 검색하는 건 B-Tree의 장점을 이용할 수 없음 😅
🎇 B-Tree 인덱스 사용에 영향을 미치는 요소
칼럼의 크기, 레코드 건수, 유니크한 인덱스 키 값의 개수 등에 의해 검색이나 변경 작업 성능이 영향을 받는다.
인덱스 키 값의 크기
- DBMS의 B-Tree는 자식 노드 개수가 가변적
- 자식 노드 개수는 인덱스의 페이지 크기(보통 단위 기본값 16KB)와 키 값의 크기에 따라 결정
- 인덱스를 구성하는 키 값의 크기가 커지면 디스크로 읽는 횟수가 증가하고 그만큼 느려진다!!
B-Tree 깊이
인덱스 키 값의 크기가 커지면, 하나의 인덱스 페이지가 담을 수 있는 인덱스 키 값의 개수가 적어지고, B-Tree 깊이가 깊어져 디스크 읽기가 더 많이 필요해진다.
선택도(기수성)
- 선택도(Selectivity) == 기수성(Cardinatlity) == 인덱스 키 값 가운데 유니크한 값의 개수
- 중복된 인덱스 키 값이 많아지면 기수성은 낮아지고 선택도 또한 감소
- 인덱스는 선택도가 높을수록 검색 대상이 줄어들어서 그만큼 빠르게 처리
읽어야하는 레코드 건수
- 인덱스를 통해 테이블 레코드를 읽는 것은 바로 테이블 레코드를 읽는 것보다 비용이 높음
- 전체 테이블을 모두 읽어 필요없는 걸 버리는게 효율적인지, 인덱스를 통해 필요한 건수만 읽는게 효율적인지 판단해야함
🌲 B+Tree 인덱스
B-Tree의 변형으로, B-Tree보다 디스크 I/O 작업 성능을 개선했다.
B-Tree는 키값과 데이터 값이 노드 안에 함께 들어가 노드 크기가 크고 디스크 I/O 작업이 많다.
따라서, B+Tree는 데이터 노드의 포인터만을 가지고, 모든 데이터는 Leaf node에 저장한다!!
🎆 Hash 인덱스
- DBMS에서 메모리 기반 테이블에 주로 구현
- 디스크 대용량 테이블용으로는 거의 사용 x
- 검색 값을 주면, 해시 함수를 거쳐 찾고자하는 키가 포함된 버켓을 찾아냄
범위 검색,동등비교조건일 경우 빠른 장점 이용 가능 (>=, <=, >, <, LIKE, BETWEEN AND / ==, IN, IS NULL, IS NOT NULL, <==>)
장점
- 실제 키값과 관계 없이 인덱스 크기가 작고 검색이 빠름
- 인덱스가 트리 구조가 아니라 버켓 하나만 읽어서 실제 레코드가 저장된 위치 파악 가능
- B-Tree보다 빠름
단점
- 함수의 결과 값 범위가 너무 넓으면 많은 버켓이 필요해 공간 낭비가 심해짐
- 해시함수를 거쳐 변형된 값을 저장해서 범위 검색, 원본값 기준 정렬이 불가능
🧨 커버링 인덱스
쿼리를 충족하는데 필요한 모든 데이터를 갖는 인덱스
- 예를 들어 (A,B) 컬럼으로 인덱스를 구성했다면
SELECT A,B FROM table WHERE A = ?와 같이 구하려는 컬럼값이 모두 인덱스에 있다면 테이블에 다시 접근하지 않아도 됨- SELECT, WHERE, ORDER BY, LIMIT, GROUP BY 등에서 사용되는 모든 컬럼이 인덱스 컬럼 안에 다 포함되는 경우
🧨 다중 칼럼(Multi-column) 인덱스
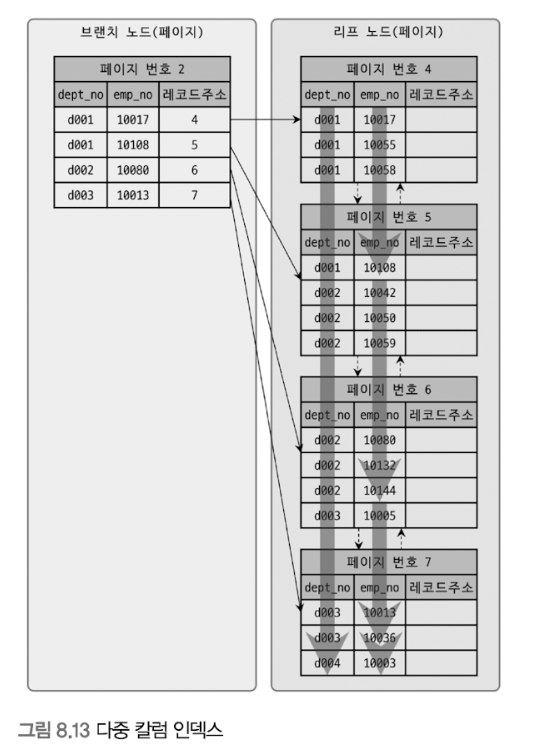
출처: Real MySQL 8.0 1권
지금까지 살펴본 인덱스들은 모두 1개 칼럼만 포함된 인덱스였다.
하지만 실제 서비스용 DB에서는 2개 이상의 칼럼을 포함하는 인덱스가 더 많이 사용된다.
다중 칼럼인덱스 == 복합 칼럼 인덱스 == Concatenated Index