머신러닝이란?

• 작업&평가를 반복하면서 결과를 개선하는 것

D1 = np.array([[1.0, 1.2, 3, 4, 5, 6], # x좌표
			  [1.7, 3, 2.3, 5.3, 3.8, 5.5]]) # y좌표
              
D2 = np.array([[-0.6, 1.0, 1.2, 3, 4, 5, 6], # x좌표
			  [2.9, 1.7, 3, 2.3, 5.3, 3.8, 5.5]]) # y좌표

• 위와 같은 두 2차원 어레이 2개가 있다고 한다면
• 좌표평면 상에 다음과 같이 나타낼 수 있음
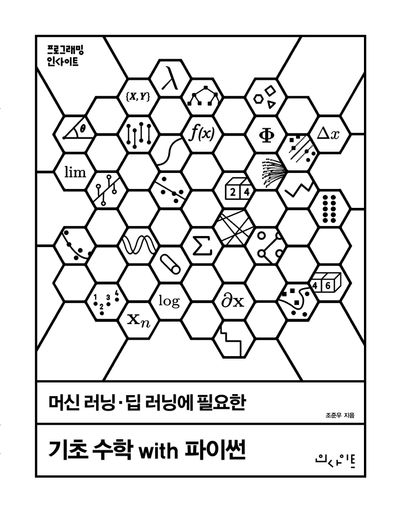
• 좌표평면 상의 점들과 가장 '친한' 선을 그리고자 한다면,
• 누군가는
  1. 여러번의 시도를 통해 그릴 수 있고
  2. 매우 똑똑하여 왼쪽 첫점과 오른쪽 끝점을 연결할 수 있음
• 또한, 머신러닝은 어떻게 선을 그릴까?

def machine_learning(D): # 노멀방정식을 통한 머신러닝 풀이
  N = D.shape[1] # N은 데이터의 갯수 (D의 shape를 떠올려보자)
  X = np.c_[np.ones(N), D[0]] # 1열에는 숫자1을 가지고, 2열에는 데이터의 x좌표를 갖는 2차원 어레이 생성, Nx2
  y = D[1] # y 좌표

  w = np.linalg.solve(np.dot(X.T, X), np.dot(X.T, y)) # 노멀 방정식을 통한 직선의 계수 구하기
  return w

def more_clever(D): # 위에서 제시한 2번과 같은 방법
  first, last = D[:,0], D[:,-1] # 첫점과 끝점

  w1 = (last[1]-first[1])/(last[0]-first[0]) # 기울기 : y증가량/x증가량
  w0 = -w1*first[0] + first[1] # 절편 구하는 식

  return (w0,w1)

def f(x,w): # 직선을 그리기 위해 입력 x와 계수 w를 입력받는 함수 정의
  return w[1]*x + w[0] # 보통 직선의 방정식을 y=ax+b로 표현하지만
  					   # 여기서는 a 대신 w[1]을, b 대신 w[0]을 사용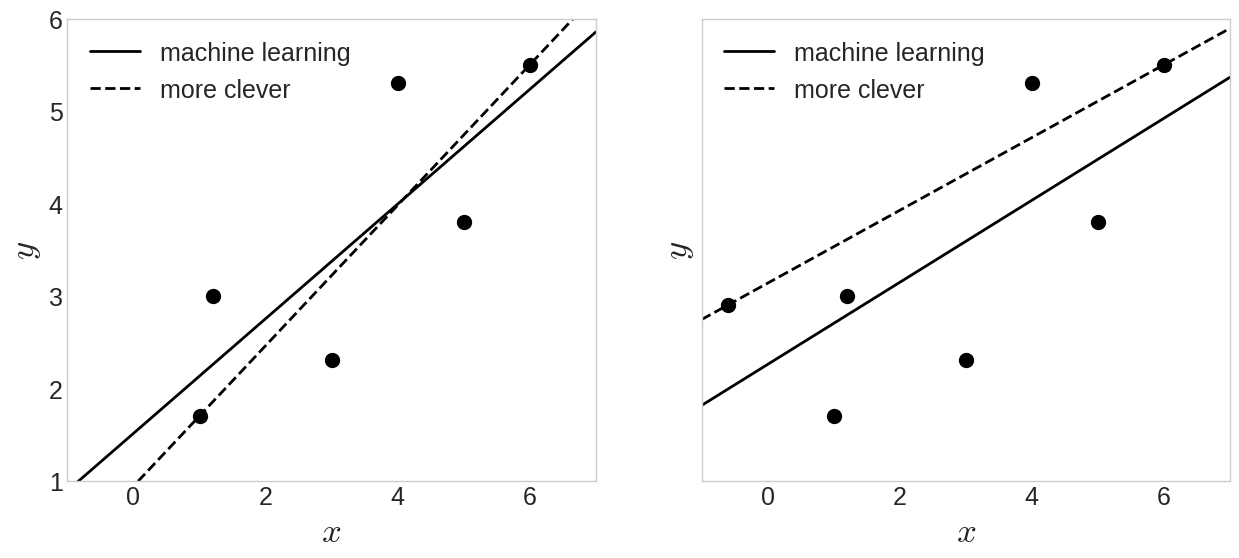

• 위에서 제시한 2번과 같은 방법(똑똑한 경우)로 오른쪽 데이터에 적용 시, 머신러닝보다 덜 친한 직선을 그리게 됨
• 따라서 머신러닝이 규칙기반 알고리즘보다 데이터에 대한 강인함과 범용성에 있어서 더 뛰어난 것을 알 수 있음

입력과 출력의 관계

• 위 직선의 의미를 생각해보면 전체 데이터에 대해 입력-출력 관계를 설명할 수 있음
• 데이터로부터 획득된 직선을 가지고 있으면 입력-출력 관계가 없던 새로운 입력 값에 대한 출력도 계산할 수 있게 됨
• 즉, 데이터로부터 입력과 출력 관계를 찾아내고 이를 통해 예측까지 하는 것

수학이 사용되는 순간

• 위에서 제시한 1번과 같은 과정을 컴픁에게 시키기 위해선 단계마다 복잡한 과정을 거쳐야 함
• 선과 점이 떨어진 정도를 계산해야 하기에 여러 수학 개념이 필요

• $point = \left(x,y\right)$ # 좌표라는 개념이 필요
• $h = ax + b$ # 직선을 수식으로
• 위의 수식을 다음과 같이 생각할 수 있음 $h = ax + b * 1$
• 입력 $(x,1)$에 적당한 수 $a,b$를 곱해서 결과를 만들어 낸다고 생각할 수 있음
• 입력 : $(x,1)$
  출력 : $ax + b * 1$
• 머신 러닝에서는 입력에 곱하는 $a,b$를 가중치weight로 자주 이야기함
• 같은 가중치 이기 때문에 벡터로 표현하며
• $h(x,\mathbf{w})=w_{1}x+w_{0}*1$ 로 표시할 수 있음
• 직선의 모양은 $w_{1}$,$w_{0}$에 의해 변하므로
• 직선을 그린다는 행동이 $w_{1}$,$w_{0}$을 결정한다는 수치적 과정으로 모델링 된 것

• 그렇다면 컴퓨터는 점과 친한 선을 그리기 위해 어떻게 이동시킬까?
• 선과 점들 사이의 수직 거리로 친함의 정도를 나타낸다면
  
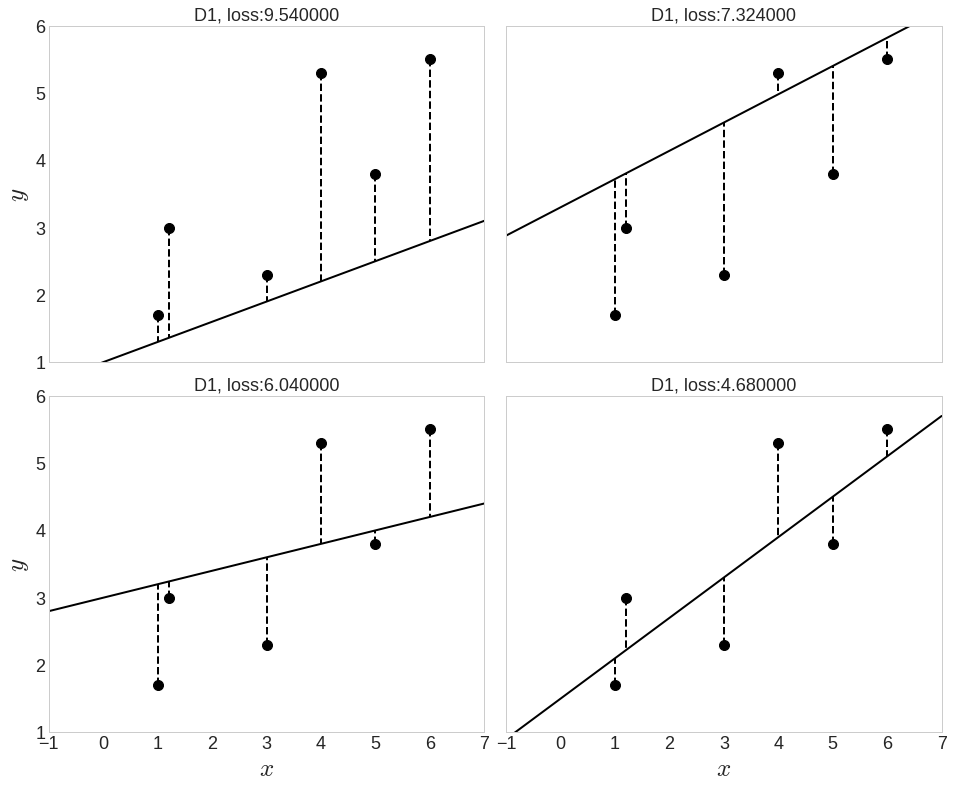
• 다음과 같은 그림을 파악할 수 있고
• 이 수직 거리를 모두 더한 총합을 손실loss라고 하며

  $L = \frac{1}{2} \sum_{n=1}^N \left\{ h(x_n, \mathbf{w}) - y_n \right\}^2$

• 손실은 점과 선이 친하지 않은 정도
• 따라서 손실을 줄이는 방향으로 $w_{1}$,$w_{0}$을 바꿔야 함
• 하지만, $w_{1}$,$w_{0}$을 잘못 바꾸면 오히려 손실 증가할 수 있음
• 그래서 우리는 손실이 감소하도록 $w_{1}$,$w_{0}$을 바꿀 수 있게 해주는 안전장치 필요
• 그것이 바로, 경사도 벡터

  $\triangledown_{\mathbf{w}}L = \frac{\partial }{\partial \mathbf{w}}\left(\frac{1}{2} \sum_{n=1}^N \left\{ h(x_n, \mathbf{w}) - y_n \right\}^2\right)$

• 위의 식을 통해 $\mathbf{w}$를 변경 시킬 수 있고, 그렇게 변경하면 절대 $L$이 커지지 않음

  $\mathbf{w}\leftarrow \mathbf{w}-\eta\frac{\partial }{\partial \mathbf{w}}\left(\frac{1}{2} \sum_{n=1}^N \left\{ h(x_n, \mathbf{w}) - y_n \right\}^2\right)$

• 위와 같이 $\mathbf{w}$를 업데이트 시킴
• 위의 과정을 코드로 표현하면 다음과 같음

num_iters = 150
alpha = 0.02

np.random.seed(2)
w = np.random.randn(2)
N = D1.shape[1] 

ws, L = [], []

# 1열에 1, 2열에 데이터의 x좌표를 가지는 행렬을 만듭니다.
# X: (N,2), y: (N,)
X = np.c_[np.ones(N), D1[0]]
y = D1[1]

# 여기서 우리의 경험 E를 반복하면서 태스크 T를 개선해 나간다.
for i in range(num_iters) :
    # grad L
    c = (1/N) * np.dot(X.T, np.dot(X, w) - y) 
    # 안전장치 grad L을 이용해서 w를 수정한다.
    w -= alpha * c 
    # w가 변화되는 과정을 저장해둔다.
    ws.append(w)
    
    # 손실을 계산한다.
    L.append( ((np.dot(X, w) - y)**2).sum()/(2*N) )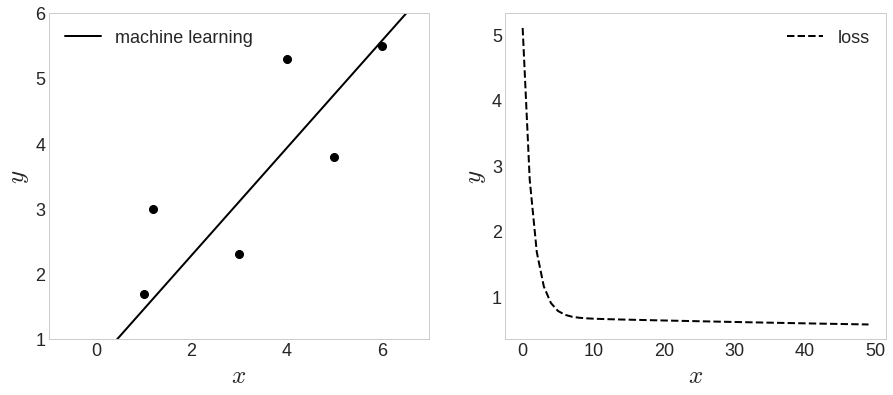

머신러닝의 분류

• 지도학습 : 입력과 출력이 있을 때, 이것들 사이의 관계를 찾아내는 과정
  ex) 분류, 회귀
• 비지도학습 : 입력과 출력이 쌍으로 주어지지 않고 입력만 사용해서 의미있는 결과를 이끌어 내는 과정
  ex) 군집화, 차원축소
• 선찾기 작업은 주어진 점들이 보여주는 분포에서 평균을 찾는 과정으로 해석할 수 있음
• 점들이 특정 분포에서 발생했다고 가정하면 이런 점들은 평균으로 회귀하는 성질이 있음
• 따라서 점들이 회귀regression하고자 하는 평균선을 찾는다고 해서 회귀라는 용어 사용

왜 선형회귀를 배울까?

• 비지도 학습의 k-최근접 이웃은 입력-출력 관계를 찾지않고 주어진 데이터를 그대로 이용함
• 선형회귀의 경우 입력-출력이 가질 것 같은 직선관계를 잘 표현하고 있음
• 위 두 모델의 차이점은, 모델을 설정하는냐 하지 않느냐의 차이
• 선긋기 예제에서 우리는 직선이라는 모델을 선택하였고, k-최근접 이웃은 그냥 주어진 데이터 기반으로 결과를 만들어 냄
• 선형회귀는 $w_{1}$,$w_{0}$이라는 분명하게 알고리즘이 결정하는 요소들이 있음
• 우리는 모델을 설정하고 관계를 찾는 알고리즘이며, 선형회귀는 그런 알고리즘의 출발점이라고 할 수 있음
• 분류를 위한 가장 기본적인 알고리즘은 '로지스틱 회귀'
• 선형회귀 출력단에 s자형 함수를 추가한 것이 로지스틱 회귀임을.. 또 이것들이 모여 '다층 퍼셉트론'까지 이어지는 흐름을 본다면 선형회귀가 딥러닝으로 가는 시발점이기에 선형회귀를 완전히 구현하고 이해하는 것이 필요