함수를 공부하기 위한 기초체력

수 체계

• 자연수 : 자연수란 사물을 셀 때나 순서를 매길 때 사용하는 수

• 정수 : 자연수에 0과 음수를 더한 것

• 유리수 : 유리수는 분자, 분모로 정수를 갖는 분수로 나타낼 수 있는 수

• 무리수 : ratio가 없는 수, 즉 비율로 표현되지 않는 수를 의미 ex) $\pi$

• 실수 : 무리수 + 유리수, 우리가 수직선을 그었을 때 그 수직선 위에 있는 모든 수

함수의 정의

• 함수란 입력과 출력의 관계를 나타내는 것

• 정의 : "공집합이 아닌 두 집합 $X, Y$에서 $X$의 각 원소에 $Y$의 원소가 오직 하나씩 대응할 때 이 대응 $f$를 $X$에서 $Y$로의 함수"

• 머신러닝에서 데이터는 X의 원소와 Y의 원소를 의미

• 지도학습이 하는 일은 그 데이터를 이용해서 왼쪽과 오른쪽의 연결관계를 찾아내는 것

입력과 출력의 관계를 설명하는 그래프

• 함수를 직교 좌표계가 아닌 밝기 그래프로 표현 가능

• 독립변수가 많아지면 밝기 그래프로 표현하는 것이 유리

합의 기호

• $\sum$의 특징

• $\sum_{i=1}^m\sum_{j=1}^na_ib_j = \sum_{i=1}^ma_i\sum_{j=1}^nb_j$

• 복잡한 시그마 기호가 등장하면 인덱스를 자세히 보고 어떤 인덱스가 어떤 시그마 기호게 영향을 받는지 살펴봐야 함

다항함수

• 함수를 도구로 사용하여 현상을 설명할 수 있도록 하는 작업을 모델링이라고 함

지수함수

거듭제곱근

• 어떤 수 x를 n번 곱했을 때, a가 되었다면 다시말해 $x^n=a$라면, 이때 a에 대한 n 제곱근은 x임

• 8의 세제곱근 = "어떤 수를 3번 곱해야 8이냐?"

• 지수함수는 매우 빠르게 증가하는 특징이 있음

자연상수 $e$

• 지수함수의 밑으로 자주 쓰이고 대표적인 무리수

• $\lim_{x \rightarrow \infty}(1+\frac{1}{x})^x = e$ or $\lim_{x \rightarrow 0}(1+x)^\frac{1}{x} = e$

로그함수

• $y = log_ax$

• a를 y번 제곱하면 x가 되는 꼴

• a를 밑, x를 진수라고 함

• $log_aMN = log_aM + log_aN$ / $log_a\frac{M}{N} = log_aM - log_aN$ (O)

• $log_aM log_aN = log_aM + log_aN$ / $\frac{log_aM}{log_bN} = log_aM - log_aN$ (X)

역함수

• y = f(x)인 함수에서 입력과 출력이 뒤바뀐 경우를 생각해 볼 수 있음

• 이 함수를 g라고 하면 x = g(y)라는 말. 이때 g를 f의 역함수라고 함

• 보통 독립변수를 x로 쓰는 관행이 있으므로 y = g(x)라고 표현

• $f^{-1}$라고 표현

• 그러나 원래의 함수가 일대일 대응일 때만 역함수가 존재, 일대일 대응이 아니라면 역함수에서 함수의 조건을 만족하지 못함

• 지수함수의 역함수 = 로그함수

• 밑이 1보다 큰 로그함수의 그래프는 매우 완만하게 증가

자주 만나는 특별한 함수 : 로지스틱 시그모이드 함수

• $\sigma(z) = \frac{1}{1+e^{-z}}$

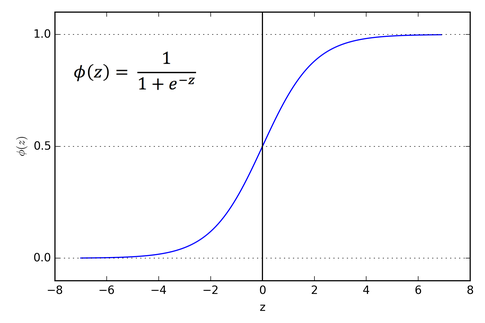
• 그래프를 보면 정의역은 실수 전체, 함숫값은 0에서 1사이

• 즉 어떤 값이 입력되더라도 0에서 1사이의 값을 출력한다는 의미

• 따라서 출력값을 확률로 해석 가능