책의 내용을 정리하다보니, 쉽게 설명한 부분에서 정확하지 않은 부분이 있을 수 있습니다.
입력과 출력에 따른 함수
스칼라와 벡터
-
스칼라 : 크기만을 가지는 값, 숫자 하나로 표현되는 값 ex)재산, 온도의 크기
-
벡터 : 크기와 방향을 모두 가지는 값, 숫자 여러 개인 값, 벡터는 기본적으로 열벡터 ex) 속도
-
일변수 스칼라함수, 일변수 벡터함수, 다변수 스칼라함수, 다변수 벡터함수
일변수 스칼라함수
- 입력 : 숫자 하나 / 출력 : 숫자 하나
일변수 벡터함수
-
입력 : 숫자 하나 / 출력 : n차원 벡터
-
경사도 벡터가 함수의 최대 증가 방향을 가리킨다는 중요한 성질을 증명하는데 사용됨
다변수 스칼라함수 = 벡터변수 스칼라 함수
-
함숫값을 최대 or 최소로 만들면 어떤 목적이 달성되는 함수를 목적함수 or 비용함수 or 손실함수라고 함, 모두 다변수 스칼라함수
-
입력 : 여러 개 / 출력 : 숫자 하나
다변수 스칼라함수의 함숫값이 고정되어 있다면?
-
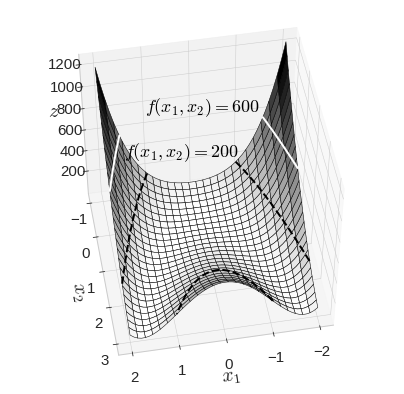
2차원에서 정의된 함수가 있고, 그 높이를 하나의 차원으로 표시한다면 3차원에 어떠한 곡면이 생길 것임
-
이변수 함수(2차원에서 정의된 함수)의 함숫값을 고정하면, 곡면에 곡선이 그어질 것
-
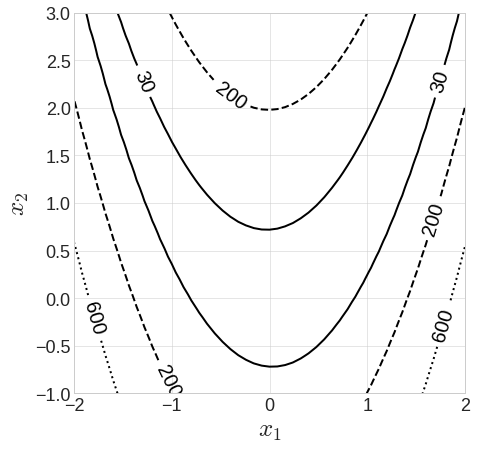
그어진 여러 개의 곡선을 등고선 그래프라 하고
-
경사도 벡터의 방향이 어느 방향인지 이 등고선 그래프를 통해 알 수 있음
다변수 벡터함수
-
대표적인 예 : 인공신경망
-
인공신경망은 딥러닝 분야의 핵심 모델
-
좀 복잡한 "다변수 벡터함수"
-
왜 복잡하냐? 출력이 입력이 되는 과정이 여러 번 반복되는 형태(층이 깊을 경우)
-
이렇게 "출력이 입력이 되는" 것을 "합성함수"라고 함
합성함수
-
머신러닝의 궁극적인 목적은 입력에 대해서 좋은 출력을 만들어 내는 모델을 만드는 것
-
그렇기 때문에 간단한 하나의 함수로는 표현할 수 없음 -> "합성함수" 사용
-
어떤 두 함수 f와 g가 있을 때, 함수 f가 집합 X의 원소 x를 집합 Y의 원소 y로 대응시키고, 함수 g가 y를 집합 Z의 원소 z로 대응시킬 때, x를 z로 대응시키는 함수를 "합성함수"라 표현함
-
로그함수의 특징 : 원래 함수의 오목, 볼록한 위치(정의역)를 변화시키지 않음 -> 확률을 기반으로 하는 머신러닝 과정에서 중요하게 사용되는 특징
소프트맥스 함수
-
대표적인 "다변수 벡터함수"
-
동일한 분모에 대해서 각 요소가 차지하는 비율이므로, 결과를 모두 더하면 1이 됨
-
이와 같은 특징으로 소프트맥스의 출력도 확률로 해석
-
다중분류문제에서 마지막 출력단을 소프트맥스 함수로 설정