[논문리뷰] SRDenseNet

고주원·2021년 6월 16일

Abstract

논문 발표 당시 이미지 super-resolution 분야는 상당히 좋은 성능을 내는 딥러닝 신경망이 많이 나왔습니다. 저자는 dense-skip connection을 활용한 딥러닝 네트워크를 제시했습니다. 제안된 네트워크는 각각의 layer의 feature map이 후속 layer에 전파됩니다. 그리고 하위 단계의 feature가 상위 단계의 feature에 결합되는 효과적인 방법을 제공합니다.
dense skip connection은 layer 각각의 output에 지름길을 직접 만들기 때문에 vanishing-gradient 문제를 예방할 수 있습니다. 또한, deconvolution layer는 업샘플링 필터를 학습하고 복원 과정에서 속도를 높이기 위해 네트워크에 통합되어 있습니다. 이는 실질적으로 파라미터의 개수가 줄고, 컴퓨팅 성능이 강화됩니다.

특징 분석

특징 분석에 앞서 논문에서는 사용한 Operation과 Optimizer, Loss function을 소개하고 넘어갔습니다. 각 convolution, deconvolution layer에는 ReLU layer를 두었습니다. Loss Function은 당시 자주 사용했던 MSE(Mean Squared Error)를 사용했습니다. Optimizer는 역시나 자주 사용하는 Adam을 사용했습니다.

DenseNet Blocks

DenseNet Block은 2017년 CVPR Best Paper 상을 받은 Densely Connected Convolutional Networks 라는 논문에서 차용한 아이디어입니다.

DenseNet Block이란

DenseNet은 종종 ResNet과 비교되곤 하는데 두 네트워크의 차이로 비교해봅시다. DenseNet의 설명은 이 분의 포스팅을 많이 참고했습니다.

ResNet은 feature map끼리 더하는 방식 vs DenseNet은 feature map끼리 결합하는 방식
결합과 더하기가 비슷한 의미라 이해를 위해 코드를 보며 짚고 넘어가겠습니다.

class ResidualBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, downsample=None):
        super(ResidualBlock, self).__init__()
        self.conv1 = conv3x3(in_channels, out_channels, stride)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(out_channels, out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.downsample = downsample
       
    def forward(self, x):
        residual = x
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        if self.downsample:
            residual = self.downsample(x)
        out += residual
        out = self.relu(out)
        return out

ResBlock은 forward의 마지막단 즈음에서 out += residual 이런 식으로 단순히 더해줍니다. 이는 아래와 같은 방식으로 계산이 됩니다.

[1,2,3] + [4,5,6] = [5,7,9]
그렇기 때문에 더하는 데 있어서 채널 개수의 차이는 발생하지 않습니다.

class Dense_Block(nn.Module):
    def __init__(self, in_channels):
      super(Dense_Block, self).__init__()
      self.relu = nn.ReLU(inplace = True)
      self.bn = nn.BatchNorm2d(num_channels = in_channels)

      self.conv1 = nn.Conv2d(in_channels = in_channels, out_channels = 32, kernel_size = 3, stride = 1, padding = 1)
      self.conv2 = nn.Conv2d(in_channels = 32, out_channels = 32, kernel_size = 3, stride = 1, padding = 1)
      self.conv3 = nn.Conv2d(in_channels = 64, out_channels = 32, kernel_size = 3, stride = 1, padding = 1)
      self.conv4 = nn.Conv2d(in_channels = 96, out_channels = 32, kernel_size = 3, stride = 1, padding = 1)
      self.conv5 = nn.Conv2d(in_channels = 128, out_channels = 32, kernel_size = 3, stride = 1, padding = 1)
    
    def forward(self, x):
      bn = self.bn(x) conv1 = self.relu(self.conv1(bn))
      conv2 = self.relu(self.conv2(conv1))
      c2_dense = self.relu(torch.cat([conv1, conv2], 1))
      
      conv3 = self.relu(self.conv3(c2_dense))
      c3_dense = self.relu(torch.cat([conv1, conv2, conv3], 1))
      
      conv4 = self.relu(self.conv4(c3_dense)) 
      c4_dense = self.relu(torch.cat([conv1, conv2, conv3, conv4], 1))
      
      conv5 = self.relu(self.conv5(c4_dense))
      c5_dense = self.relu(torch.cat([conv1, conv2, conv3, conv4, conv5], 1))

      return c5_dense

DenseBlock은 c2_dense = self.relu(torch.cat([conv1, conv2], 1)) 이런 식으로 concat연산을 해주는데 아래와 같은 방식으로 계산이 됩니다.

[1,2,3] + [4,5,6] = [1,2,3,4,5,6]
이해하기 어려웠었는데 out_channel과 in_channel의 개수를 보고 힌트를 얻었습니다.
conv3 = self.relu(self.conv3(c2_dense)) 을 보면 들어가는 in_channel의 개수가 64개입니다. 만약 단순히 conv2를 넣어주는 형태였다면, 차원의 개수가 다르기 때문에 에러가 떴을 것입니다.
c2_dense에서 conv1과 conv2를 concat 연산을 해서 합쳐줬기 때문에 32+32로 64개의 차원이 되었기 때문에 정상적으로 동작 한 것입니다.
실제로 document에서 torch.cat의 예제를 보면

>>> x = torch.randn(2, 3)
>>> x
tensor([[ 0.6580, -1.0969, -0.4614],
        [-0.1034, -0.5790,  0.1497]])
>>> torch.cat((x, x, x), 0)
tensor([[ 0.6580, -1.0969, -0.4614],
        [-0.1034, -0.5790,  0.1497],
        [ 0.6580, -1.0969, -0.4614],
        [-0.1034, -0.5790,  0.1497],
        [ 0.6580, -1.0969, -0.4614],
        [-0.1034, -0.5790,  0.1497]])
>>> torch.cat((x, x, x), 1)
tensor([[ 0.6580, -1.0969, -0.4614,  0.6580, -1.0969, -0.4614,  0.6580,
         -1.0969, -0.4614],
        [-0.1034, -0.5790,  0.1497, -0.1034, -0.5790,  0.1497, -0.1034,
         -0.5790,  0.1497]])

이런식으로 병합? 결합? 해주는 형태의 연산을 해주게 됩니다.
c5_dense 에선 결국 앞서 했던 모든 convolution을 합쳐서 연산하게 됩니다. (이런 특징 때문에 조밀하다[dense]는 이름을 붙인게 아닐까요?)
Dense Block을 통해 얻을 수 있는 이점은 다음과 같습니다.
1. Vanishing Gradient 개선
2. Feature 전파 강화
3. Feature 재사용
4. Parameter 수 절약

Deconvolution layers

SRCNN과 VDSR의 경우에는 bicubic Interpolation을 진행 한 후에 SR 연산을 진행합니다.
이는 컴퓨터 자원 소모가 많이 발생하게 됩니다.
또한 Interpolation 접근법은 SR 문제에서 새로운 정보를 가져오지 않습니다.
이 부분은 보간이 늘어난 만큼 연산량은 증가하지만, 단순 연산을 통해 얻어진 결과이기 때문에 그것이 의미있는 정보가 아니라는 뜻으로 이해했습니다.
기존 보간법들은 공식이 정해져서 feature 정보를 늘리기 보다는 단순히 숫자만 늘어난 결과를 낳게됩니다.
논문에서는 upsampling시에 이미지의 정교한 복원을 위해서 Deconvolution layer를 차용했습니다.
Convolution Layer와 Deconvolution Layer
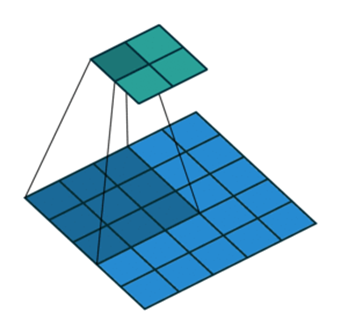
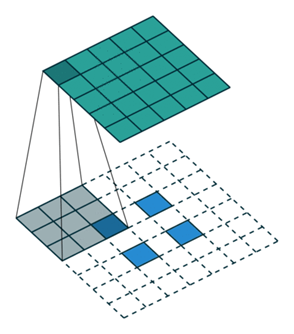
- 간단하게 짚고 넘어가자면, Convolution 연산은 feature map이 줄어들면서 압축된다면,
- Deconvolution 연산은 그 반대로 feature map을 늘려준다.
Deconvolution Layer는 두가지 이점이 있습니다.

SR 복원 과정이 빨라집니다.
- Deconvolution Layer는 네트워크의 끝에서 더해지는데, 이 전체 계산 과정이 LR 공간에서 수행됩니다.
- 만약에 Upscaling factor가 $r$ 이라면 보간을 한 이후에 계산 과정이 진행됩니다. 그러면 $r^2$ 만큼 계산량이 증가하게 됩니다. Deconvolution Layer에서는 $r$ 만큼만 계산하면 됩니다.
High frequency에 대한 디테일을 살릴 수 있습니다.

Combination of feature maps

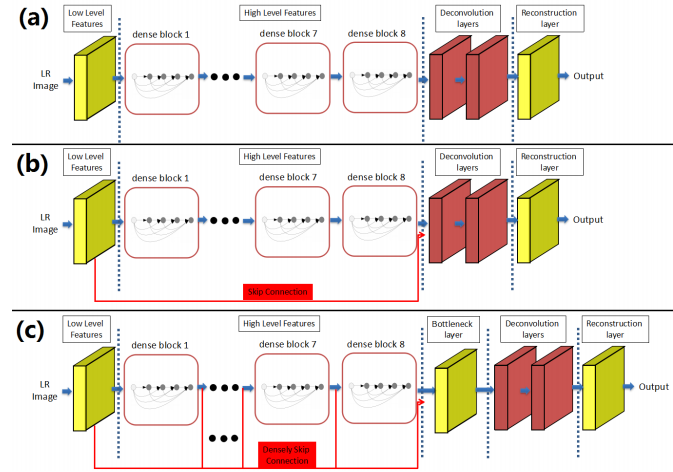
논문은 (a)를 SRDenseNet_H, (b)를 SRDenseNet_HL, (c)를 SRDenseNet_ALL이라고 명명했습니다.
(a)의 경우에는 Top Layer에 feature map만이 존재하는 단순 모델입니다.
(b)는 (a)에 Skip Connection이 추가되어서 Low-level과 High-level이 합쳐집니다.
(c)는 모든 feature map이 연결되어서 Deconvolution layer에 전달합니다.
PSNR과 SSIM으로 비교한 결과에 따르면 (c)>(b)>(a) 순의 성능 차이가 있습니다.

Bottleneck and Reconstruction Layers

앞서 보았던 (c) 모델은 모든 Feature map이 연결되어 Deconvolution에 많은 입력을 제공합니다.
다만, 많은 수의 Feature map이 직접 Deconvolution layer에 들어간다면 계산 비용과 모델 크기가 크게 증가합니다.
따라서 모델 간결성을 유지하고 계산 효율성을 향상시키기 위해서 1x1 크기의 커널을 가진 Convolution Layer를 거치게해 입력되는 feature map의 수를 줄일 수 있습니다.
이를 병목계층이라고 합니다.

고주원

Deep learning for super-resolution

이전 포스트

[논문리뷰] EDSR

다음 포스트