chap02 모델 평가 및 선택

이상민·2023년 9월 13일

2.1 경험 오차 및 과적합

Training error: 모델이 학습 데이터셋에서 만들어낸 오차
Generalization error: 모델이 새로운 데이터 셋에서 만들어 낸 오차
Overfitting: 모델이 특정 훈련 데이터의 특성을 과하게 학습하여 특정 데이터의 특성을 일반적인 성질이라 혼동하는 것
Underfitting: 모델이 훈련 데이터의 일반 성질을 제대로 학습하지 못한 것

모델 학습시 우리의 목표는 학습오차와 일반화 오차 중 일반화 오차를 줄이는 것이 목표이다. 그러나 사전에는 새로운 데이터 셋에 대한 정보를 얻을 수 없기 때문에, 훈련 오차(training error)를 최소화 하는 것이다.

편향과 분산 Trade Off

bias(편향): 예측값과 실제 값이 서로 먼 정도를 나타냄
variance(분산): 예측값들이 서로 떨어저 있는 정도를 나타냄

왼쪽 그래프의 경우 점선으로 표시된 예측값과 실제값들은 서로 멀리 떨어져있고(편향이 높다) 예측값들이 서로 가까이 붙어 있다(분산이 낮다) 분산과 편향이 둘다 낮은 것이 좋은 모델이지만 둘 중 하나를 줄이면 나머지 하나는 증가하는 상충관계이다.
해결법

Underfitting: 신경망 모델의 경우 epoch를 늘리거나, 의사결정트리는 가지치기를 늘린다.
Overfitting: 과적합은 인공지능이 넘어야할 핵심 장애물인 만큼 과적합을 해결하는 방법은 없다. early stop, ensemble, 작은 모델 사용 등등 "완화"하는 방법 밖에 없다.

2.2 평가 방법

모델의 일반화 성능을 평가하기 위해 다양한 방법으로 모델을 평가한다. 평가하는 방법을 배워 보자

2.2.1 홀드 아웃

데이터 세트 D를 겹치지 않는 임의의 두 집합으로 나누어 평가를 진행.

주의
train/test 데이터 셋을 나눌 때 되도록이면 데이터 분포가 같게 나눠야한다. 그렇지 않으면 데이터의 편향에 의해 의도치 원치 않은 결과를 얻을 수 있다.

Stratified Sampling을 이용하자!

2.2.2 교차검증

교차검증 cross validation은 데이터 세트 D를 k개의 서로소 집합으로 나누는 것으로 시작한다. 되도록 부분 집합은 D의 데이터 분포를 반영하도록 나눈다. 그 후에 k-1개의 부분집합들을 train set으로 사용하고 나머지는 테스트 데이터 세트로 사용한다.

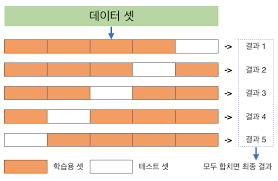
이후 p번의 교차검증을 실행한 값의 평균을 최종 평과 결과로 사용한다

2.2.3 부트스트래핑

2.2.4 파라미터 튜닝과 최종 모델

2.3

2.3.2 재현율, 정밀도 그리고 F1 스코어

평가지표로써 오차율(error)과 정확도(acc)는 자주 사용되지만 모든 문제에 활용 되지는 못한다.

사기를 검출하는 모델이 있다고 생각해보자. 데이터셋은 사기인 데이터와 사기가 아닌 데이터 샘플이 1:9의 분포를 갖는 불균형데이터 셋이다. 여기서 만약에 모델이 모두 사기가 아니다(False)로 예측한다면 모델의 정확도는 0.9로 매우 높은 정확도를 갖으므로 좋은 모델인 것 처럼 보이지만 재현율과 정밀도로 평가하면 그렇지 않다. (정밀도: $\infty$ , 재현율: 0)

정밀도(precision): 양성이라고 예측한 것들 중 실제 양성인 비율
재현율(recall): 실제 양성인 데이터 중 양성이라고 예측한것의 비율

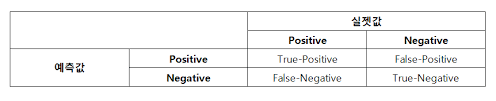
정밀도 P와 재현율 R 공식

$Precision=\frac{TP}{TP+FP}$ (양성이라 예측한 것 중 실제 양성인 비율)

$Recall=\frac{TP}{TP+FN}$ (실제 양성인 데이터중 양성이라 예측한 비율)
정밀도와 재현율의 Trade Off

정밀도와 재현율 사이에서도 트레이드 오프가 존재한다. 일반적으로 정밀도가 높으면 재현율이 낮고 재현율이 높으면 정밀도가 낮다.
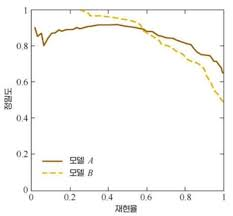
PR Curve

PR curve란 Threshold를 줄여가면서 precision과 recall에 대해 그린 곡선이다. 다양한 모델 혹은 다양한 하이퍼 파라미터를 조절해가며 PR curve를 그리면 모델 간 성능을 직관 적으로 비교해 볼수 있다.
P-R Curve 그리는 법

1. 모델의 모든 예측값을 Probability 기준으로 내림차순 정렬한다.
2. 가장 높은 Probability를 갖는 샘플의 Probabilitty를 Threshold로 정한다.
3. 2번에서 정한 Threshold를 기준으로 Precision, recall을 구한다.
4. 이후 다음으로 높은 Probability를 갖는 샘플을 Threshold로 정하여 다시 precision,recall을 구한다
5. 모든 샘플에 대하여 반복한 뒤 구해 놓은 (Recall, Precision)을 좌표로 그래프를 그린다.

f1 score
재현율과 정밀도의 조화 평균

$F_1 = \frac{2PR}{P+R}$

2.3.3 ROC와 AUC

ROC - Curve
ROC-Curve는 TPR(Recall) 과 FPR(False Posivive Rate)의 관계를 나타내는 그래프이다. (0,1)에 가까울 수록 좋은 모델이다.

$TPR=\frac{TP}{TP+FN}$ (실제 양성인 데이터 중 양성이라 예측한 샘플의 비율)
$FPR=\frac{FP}{FP+TN}$ (실제 음성인 데이터 중 음성이라 예측한 샘플의 비율)

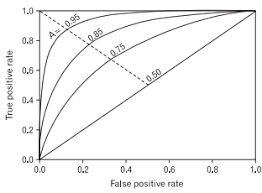
AUC
Area Under ROC Curve의 약자로 ROC커브의 면적을 의미한다. 주로 두 모델의 ROC curve가 교차하여 비교하기 어려울때 사용한다.

- AUC 공식: 만약 ROC곡선이 각 좌표로 $\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$ 로 이루어 졌다고 가정한다면.

$AUC=\frac{1}{2}\sum_{i=1}^{m-1} (x_{i+1}+x_{i})(y_{i+1}+y_{i})$

ROC, P-R 정리

P-R Curve
- 불균형 데이터셋에 적합: PR-Curve에 경우 불균형 데이터셋에 대한 평가로 적합한데, 특히 양성 클래스 성능에 대해 더 민감하다.
- 양성 클래스에 초점: PR-curvesms 양성 클래스에 대해 민감하기 때문에 질병 탐지, 사기 탐지와 같은 이상 탐지에 적합하다.
- 임계값 조절: 어떠한 임계값이 적합한지 찾을 수 있다.
ROC Curve
- 균형 데이터셋: 양성, 음성 클래스 분포가 비슷한 데이터셋에 적합
- 일반적인 상황에 적합: 이상탐지가 아닌 일반적인 상황(랭킹, 추천)과 같은 Task를 평가하는데 적합