3.1 기본형식

$d$ 개의 속성을 가진 샘플 $x = (x_1,x_2,x_3,...x_d)$이고, $x_i$는 $x$의 $i$번째 속성이라고 가정한다면 선형모델의 식은 다음과 같다.

$f(x) = w_1x_1 + w_2x_2 + ... w_dx_d + b$
이 식을 벡터로 정의하면 다음의 수식이 된다.
$f(x)=w^Tx+b$

위 식에서 $w$와 $b$를 학습한 후 모델이 결정 된다.

3.2 선형 회귀

선형회귀(linear regression)는 최대한 정확하게 실제 데이터를 예측하는 선형 모델을 학습하는 것을 목표로한다.
앞서 말했 듯 선형 회귀는 $f(x_i)=wx_i+b$ 함수를 학습해 $w,b$를 조정해가며, $f(x_i)\simeq y_i$을 얻는다.

그렇다면 위 식에서 $w$와 $b$는 어떻게 정해질까? 선형 회귀에서는 평균 제곱 오차를 최소화 하는 방식으로 w,b를 조절한다.

$E_{(w,b)}=argmin{\sum_{i=1}^m}(f(x_i)-y_i)^2$

$w$와 $b$를 찾기 위해 $w$와 $b$에 대해 미분하면 다음과 같은 식을 얻을 수 있다.

• 식(1)

$\frac{\delta E_{w,b}}{\delta w} = 2(w\sum_i^mx_i^2-\sum_i^m(y_i-b)x_i)$

• 식(2)

$\frac{\delta E_{w,b}}{\delta w} = 2(mb-\sum_i^m(y_i-bx_i))$

그리고 식 (1)와 (2)을 0으로 만들어 $w$와 $b$ 최적해의 닫힌해를 구할 수 있다.

• 식(3)

$w=\frac{\sum_i^m(y_i-m)}{\sum_ix^2-\frac{1}{m}(\sum_{i=1}^mx_2)^2}$
$b=\frac{1}{m}{\sum_i^m(y_i-bx_i)}$
$m$은 $x$의 평균

3.2.2 최소 제곱법

최소 제곱법을 사용해서 바로 구할 수도 있다

https://subprofessor.tistory.com/104

하지만 최소 제곱법을 사용하기 위해서는 $X^TX$의 역행렬이 존재하기 때문에 햔실에서는 사용하기 어렵다.
(예를 들어 feature 보다 샘플의 수가 많은 경우 즉 행보다 열이 많은 경우와 같은 상황.)

3.3 로지스틱 회귀

앞서 선형 모델을 사용하여 회귀학습하는 방법에 대해 알아 보았다. 선형 모델을 이용하면 회귀문제 뿐만 아니라 분류문제까지 학습할 수 있는데, 시그모이드 함수를 이용하여 선형 회귀 모델의 예측값을 연결해 주면 된다.

결과값이 $y\in \{0,1\}$인 이진 분류 분제라고 가정해보자.
선형회귀 모델이 생성한 예측값 $z=w^Tx+b$는 연속적인 값을 갖는 실수이다.
따라서 우리는 연속적인 실수 $z$를 {0,1}의 값으로 변환해 주기 위해 시그모이드함수를 활용한다.

• 시그모이드 (sigmoid)함수
  시그모이드 함수는 (0,1)의 범위를 갖는 함수로 회귀모델의 예측값을 활용하여 sigmoid의 값이 0.5 이상이면 True 이하는 False으로 간주한다.

$y = \frac{1}{1+e^{-z}}$

$z = w^Tx + b$

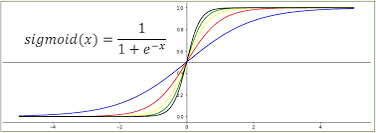
시그모이드함수를 다음식으로 바꿀 수 있다.

$y = \frac{1}{1+e^{-(w^Tx + b)}}$
$y(1+e^{-(w^Tx + b)) }= 1$
$\frac{1}{y} = 1+e^{-(w^Tx + b)}$
$\frac{1-y}{y} = e^{-(w^Tx + b)}$
$\ln\frac{1-y}{y} = -(w^Tx + b)$
$\ln\frac{y}{1-y} = (w^Tx + b)$

• Odds
  위 식에서 $\frac{y}{1-y}$은 odds라고 하며 만약 y를 샘플 $x$가 양성일 확률로 본다면 $(1-y)$는 반대로 음성 값일 확률이다. odds는 $x$가 양성일 상대적인 가능성을 나타낸다.

  예를 들어 $x$가 양성일 가능성이 $\frac{2}{3}$ 이라면 odds는 $\frac{2}{1}$이며 이는 1 번 음성(분모)이면 2번(양성) 분자일 것이다라는 의미로 해석됨

• logit (log odds)
  odds에 log를 취한것이 log odds 또는 Logit이라 부른다

  $\ln\frac{y}{1-y}$ -----------logit

• logit 근사
  아래 식에서 알 수 있듯이 선형회귀의 예측값은 실제 데이터의 logit에 근사한다. 따라서 이러한 모델을 logistic regression 혹은 logit regression라고 부른다

  $\ln\frac{y}{1-y} = (w^Tx + b)$

참고: https://nittaku.tistory.com/478

‼️ 주의: 로지스틱 회귀는 '회귀'지만 사실상 일종의 분류 학습법이다. 이러한 방법은 많은 장점이 있다.
예를 들어 이러한 모델은 분류 가능성에 대해 .......(보충할 예정 p.72)

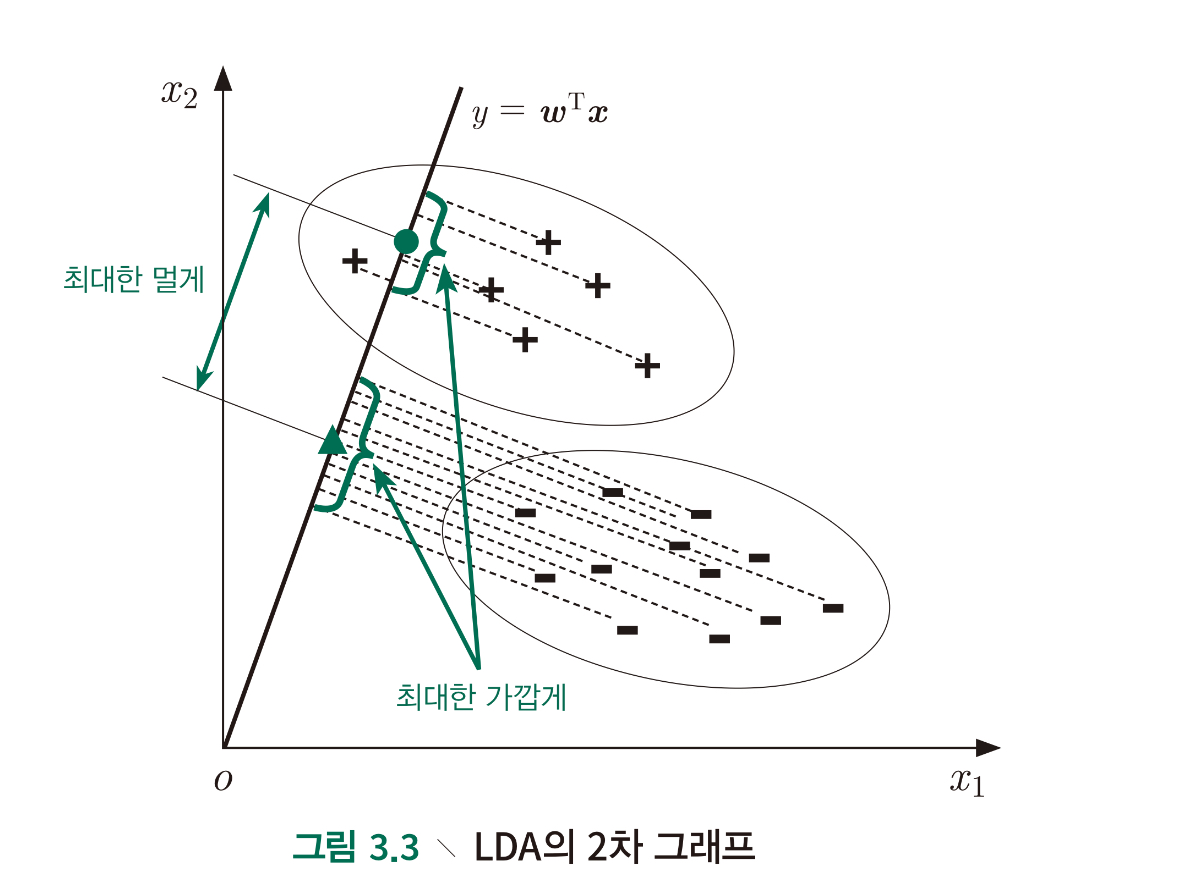
3.4 선형 판별분석

선형판별분석(Linear Discriminant Analysis, LDA)는 전통적인 선형 학습법이다.

• 학습

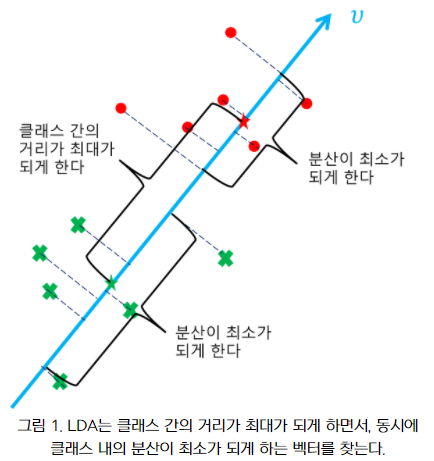
  LDA는 훈련 데이터 세트를 정하고 샘플을 하나의 직선 위에 투영시키는 것이다. 같은 클래스에 속하는 샘플을 가능한 가까운 투영점에 놓고 서로 다른 클래스에 속한 샘플들은 최대한 먼 위치에 위치 하도록 한다.

• 예측

  새로운 데이터에 대해 분류를 진행할 때 해당 직선 상에 투영 되도록하며 투영된 위치에 따라 데이터의 클래스를 분류한다.

3.5 다중 분류학습