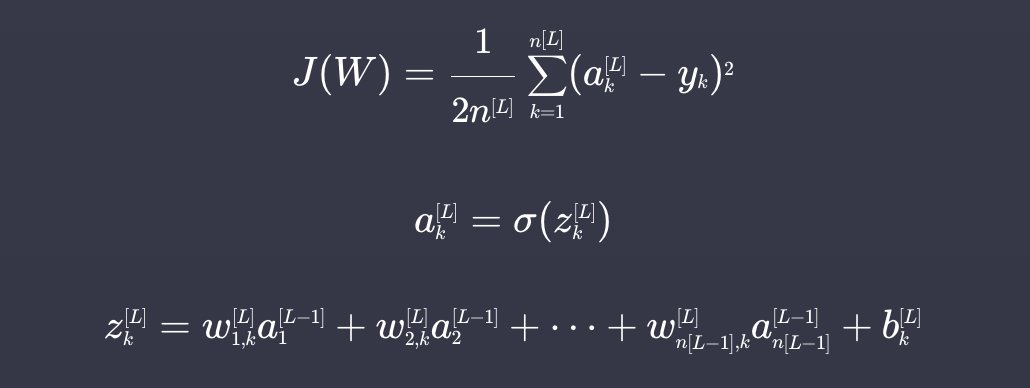역전파

역전파란?

역전파란 딥러닝 신경망의 가중치와 편향들에 대한 손실함수의 편미분 값을 구하는 방법이다. 역전파의 핵심은 출력에 대한 편미분 값을 앞 층에 전달하는 것이다.

연쇄법칙

딥러닝의 손실함수는 복잡한 합성함수이기 때문에 연쇄법칙을 사용하여 미분한다.

만약 $\frac{df}{dx}$를 구하고 싶으면 아래와 같은 과정을 통해 구할 수 있다.

$f(y)=y^3, y(x)=x^2+2x+1$

$\frac{df}{dy}=3y^2, \frac{dy}{dx}=2x+2$

$\frac{df}{dx}=\frac{df}{dy}*\frac{dy}{dx}=(2x+2)*3y^2$

편미분 계산

• 가중치에 대한 편미분: 앞층의 i번 째 뉴런과 j번 뉴런을 연결하는 가중치 $w^L$를 바꾸면 앞층의 $a_j^L$에만 영향을 미치기 때문에 $w$를 바꿀때 $z,a,j$가 어떻게 바뀌는지 계산하여 곱함
  

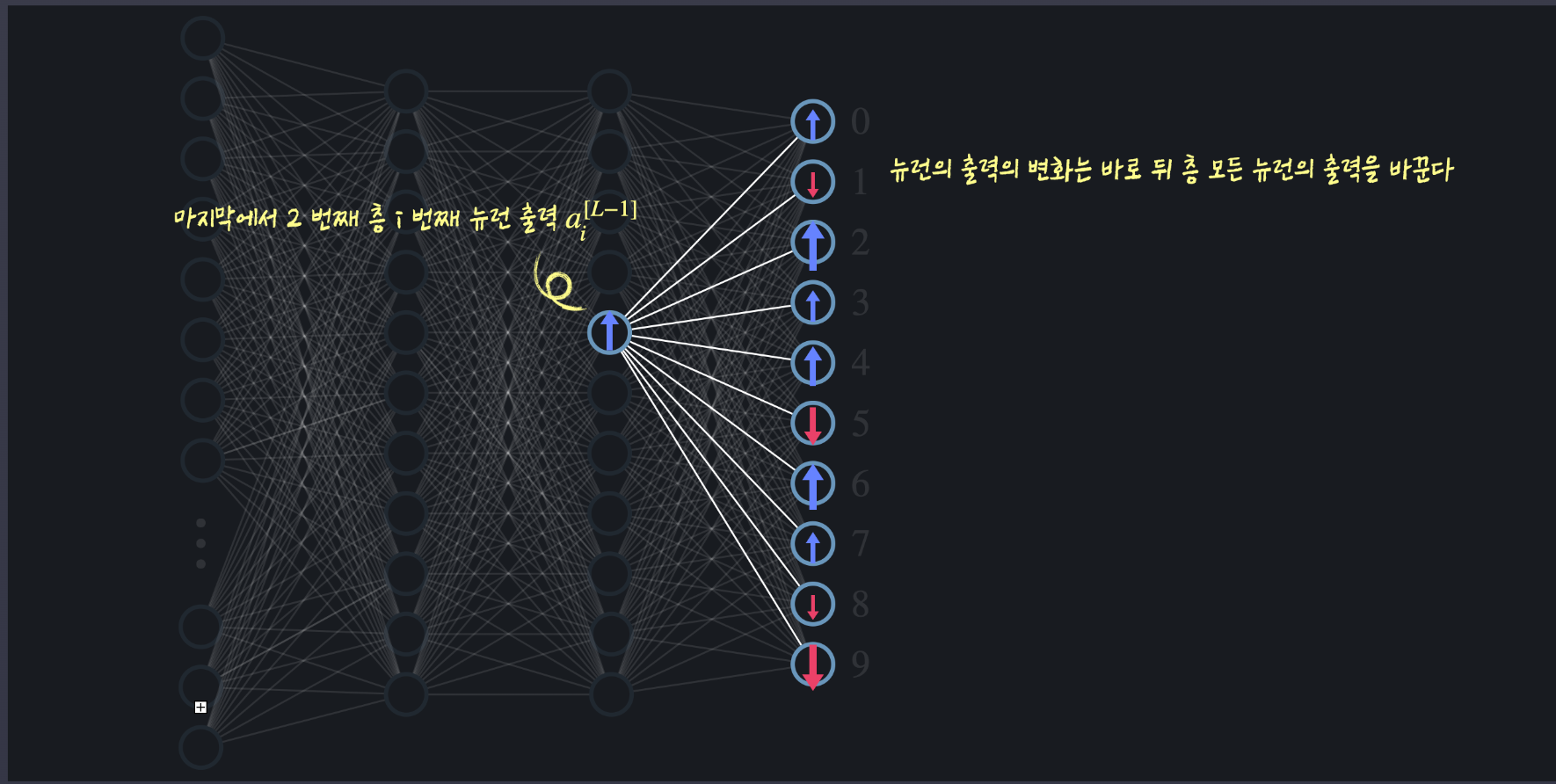
• 이전 층의 뉴런에 대한 편미분: 가중치와 편향이 바뀌면 뒷층 하나의 뉴런에만 영향을 미치지만, 전층뉴런의 출력을 바꾸면 뒤층 모든 뉴런의 출력에 영향을 미침

  

• 공식
  

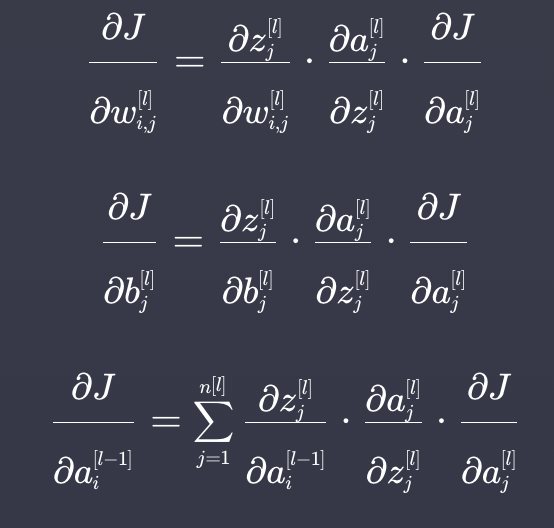
정리

역전파는 신경망에서 각 가중치와 편향에 대한 손실 함수와 편미분, 즉 가중치와 편향을 바꿀 때 손실함수가 어떻게 바뀌는지를 계산하는 과정이다.