경사하강법(gradient descent method)

경사하강법

경사하강법이란 미분을 이용하여 손실함수의 최솟값을 찾아가는 iterative한 방법이다.

경사하강법목적

인공지능 모델을 검증할 때 예측값과 레이블(정답)값의 오차를 나타내는 손실함수를 이용하여 검증하는데 손실함수 값이 작을 수록 모델의 오차가 적다. 머신러닝,딥러닝에서 사용하는 손실함수는 간단하지 않고 매우 복잡한 경우가 많아 미분값을 구하기 어려운 경우가 많다. 경사하강법을 사용하면 손실함수를 최소화 시킬 수 있는 파라미터를 효율적으로 찾을 수 있다.

경사하강법 수식 유도

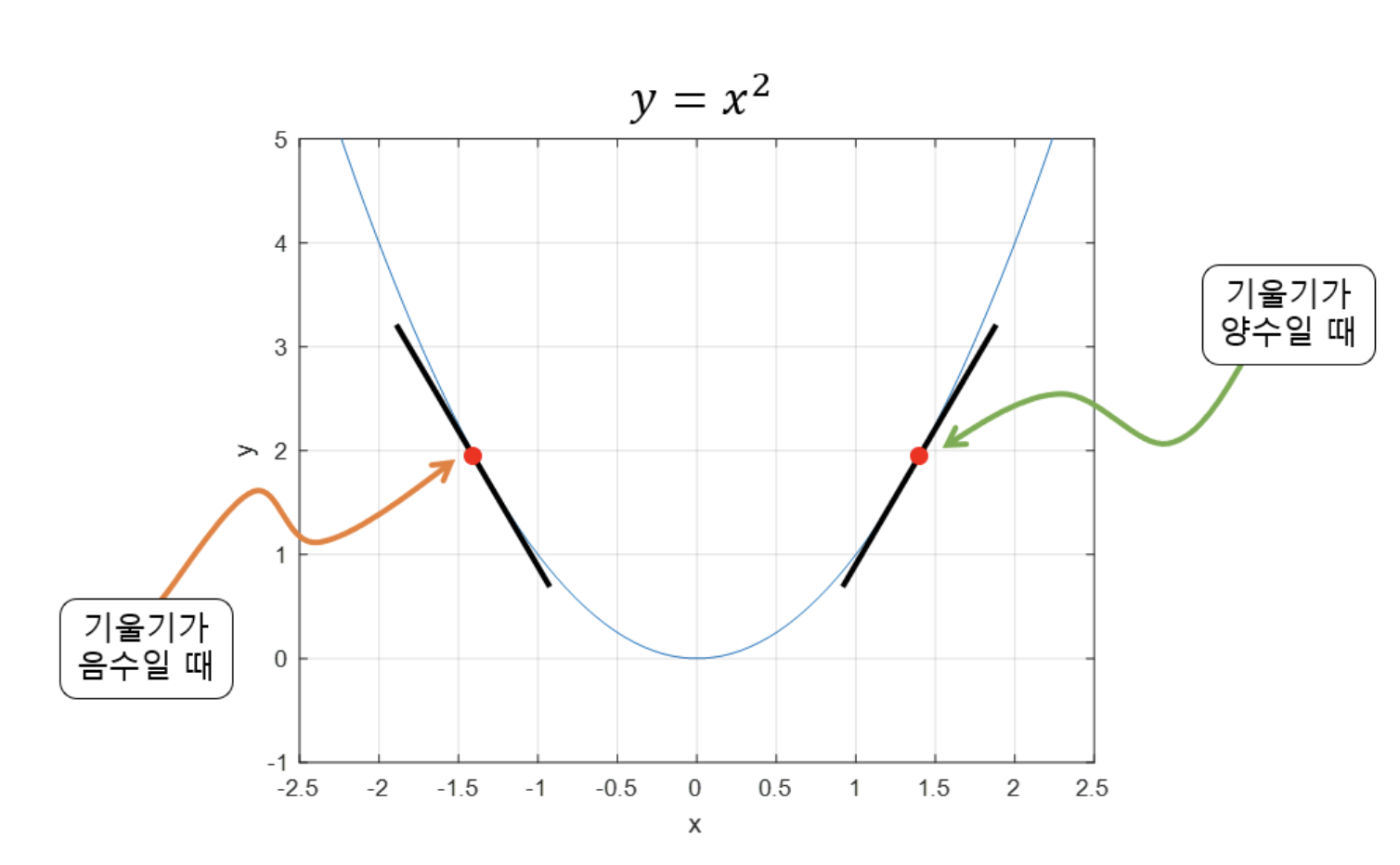
• $f'(x) > 0$: 기울기가 양수 일때 $x$값이 작아질 수록 함수값이 작아짐

• $f'(x) < 0$: 기울기가 음 일때 $x$값이 커질 수록 함수값이 작아짐

  	따라서 _해당 파라미터에서 기울기를 빼면 최솟값이 되는 장소를 찾을 수 있다.

$x_i=x_i-l*f'(x_i)$

경사하강법의 한계

선형회귀의 손실함수의 경우 미분가능하고 convex하므로 수렴이 보장된다. 하지만 비선형 회귀에 경우 손실함수가 항상 convex하지 않을 수 있으므로 수렴이 항상 보장 되지는 않는다.

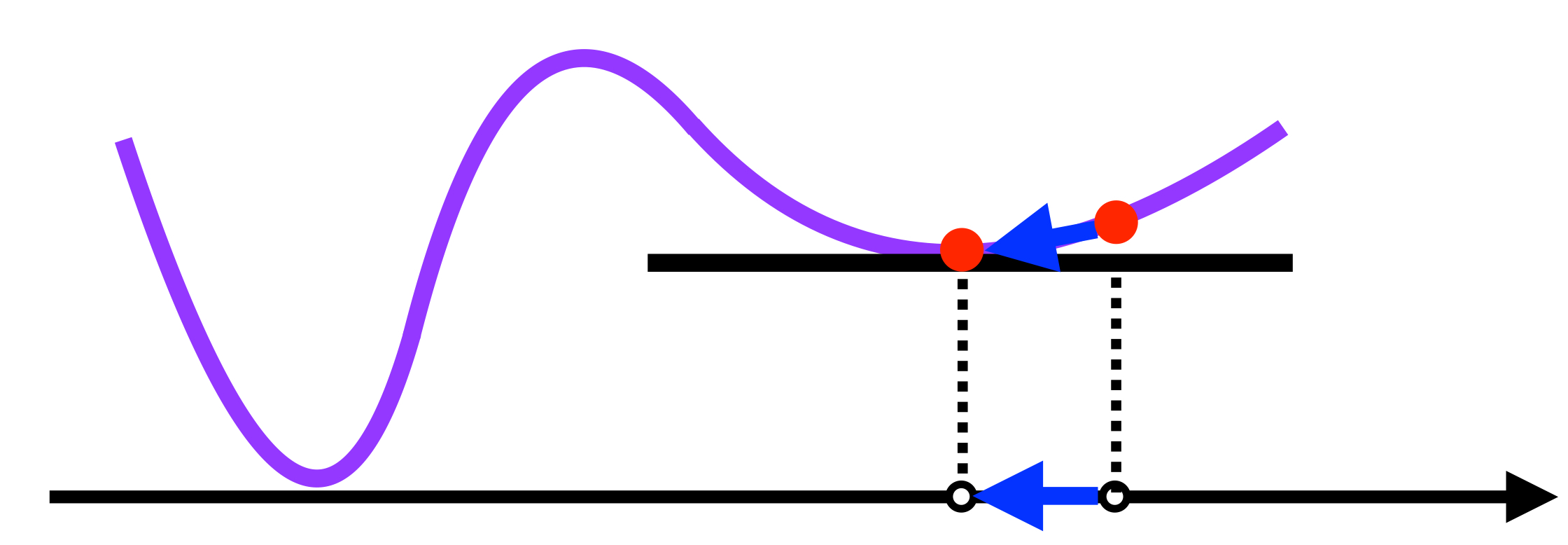
• 그림처럼 현재 수렴하고 있는 값이 global minima이 아닌 local minima 일 수 있다.