최적화 알고리즘

앞서 배운 경사하강법을 바탕으로 딥러닝 학습을 빠르게하는 최적화 알고리즘에 대해서 배워보자.

Mini-batch gradient descent

미니배치 경사하강법은 전체훈련 데이터를 미니배치로 나누어 미니배치에 대하여 경사하강법을 진행하는 기법이다. Mini-batch gradient descent(MGD)는 전체 데이터에 대해 학습을 진행하는 Batch-gradient descent(BGD) 보다 빠르게 학습을 진행할 수 있는 장점이 있다.

MGD pseudo

미니배치 경사하강법의 의사코드는 다음과 같다.

• $X$: 전체 5,000,000개의 학습 데이터
• $X[t]$: 전체 데이터 X를 1,000개씩 나눈 mini-batch
• $y[t]$: $X[t]$에 대응하는 labels

    for t in range(5000) # forward on X[t]
    	Z[1] = W[1]X[t] + b[1]
        A[1] = activate(Z[1])
        ...
        A[l] = activate(Z[l]) #순전파 진행
        
        compute loss
        Backprop # 역전파 계산
        optm.step() # weight update

코드를 보면 5000개의 미니배치에 대해 각각 forward prop와 backward prop를 진행하는 것을 알수 있다

MGD cost graph

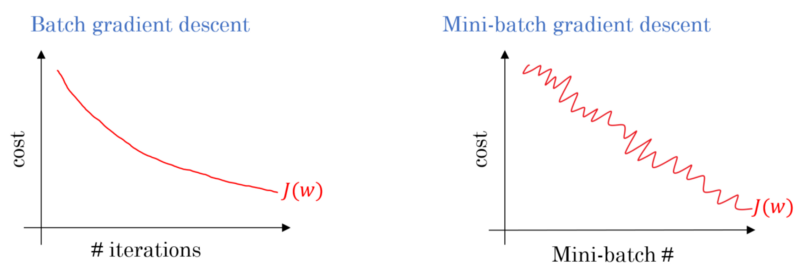
MGD를 진행하면 cost 값은 위 그래프와 같이 진동하면서 전체적인 흐름은 감소한다. 이러한 결과가 나오는 까닭은 미니배치마다 데이터의 분포가 달라서mini-batch에 noise가 껴있거나 mini-batch각각 난이도가 달라 cost가 적게 나올 수도 크게 나올 수도 있기 때문이다.

Choosing mini-batch size

전체 m개의 학습 데이터가 있다고 가정할때

Mini-batch-size = m : Batch Grandient decesent
Mini-batch-size = 1: Stochastic Gradient Descent

만약 batch size를 크게 설정한다면 학습하는 데 매우 오랜 시간이 걸릴 수있다. batch size를 작게 설정한다면 적은 샘플만 처리한 뒤에 진행할 수 있어 매우 간단하지만 gpu 병렬 연산의 장점이 사라진다.

따라서 1과 m 사이 적절한 값을 찾아야 된다.

choosing size
if small train set (m<2000): BGD 사용
Typical minibatch size
64,128,256,512 와 같이 2의 n승 단위로 설정
미니배치의 사이즈가 cpu, gpu 메모리에 맞는지 확인해야된다.

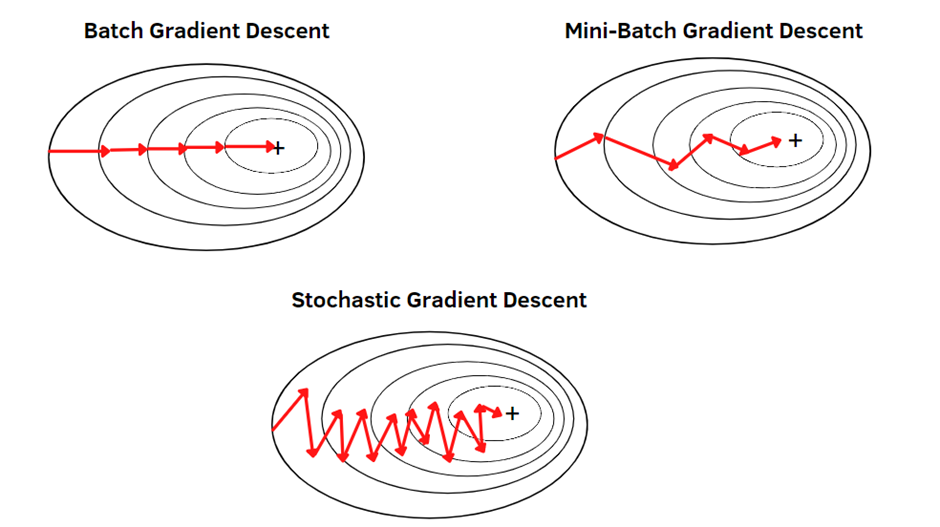
Exponentially weighted averages(지수가중이동평균)

이후에 효율적인 최적화 알고리즘을 배우기 위해 우선 지수 가중 이동평균을 이해해야 된다.

지수가중평균
데이터의 이동 평균을 구할 때, 오래된 데이터가 미치는 영향을 지수적으로 감쇠(exponential decay) 하도록 만들어 주는 방법.

• 즉 오래된 데이터가 현재 데이터에 미치는 영향을 줄이도록 하는 방법

런던 날씨 예시

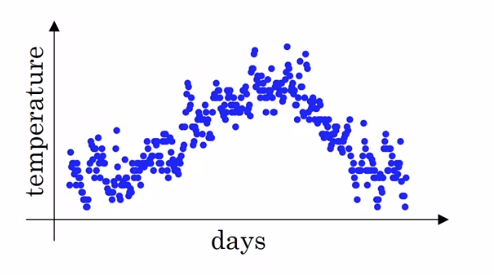
만약 런던 날씨에 대한 날짜와 날씨에 대한 산점도가 위 그래프와 같다. 이 데이터는 noisy해서 최신 트랜드를 산출하기 위해서는 지수가중 평균을 이용해야한다.

$V_t = β×V_{t-1} + (1−β) ×{\theta}_t$
$V_{t−1} = β×V_{t−2} + (1−β) ×{\theta}_{t−1}$

• β: 0 ~ 1의 값을 갖는 상수
• ${\theta}_t$: t 시점의 현재 데이터 (온도)
• $V_t$: 현재 경향을 나타냄

만약 ${\beta}$를 0.9로 설정하고 지수가중 평균을 구하면 다음과 같다.

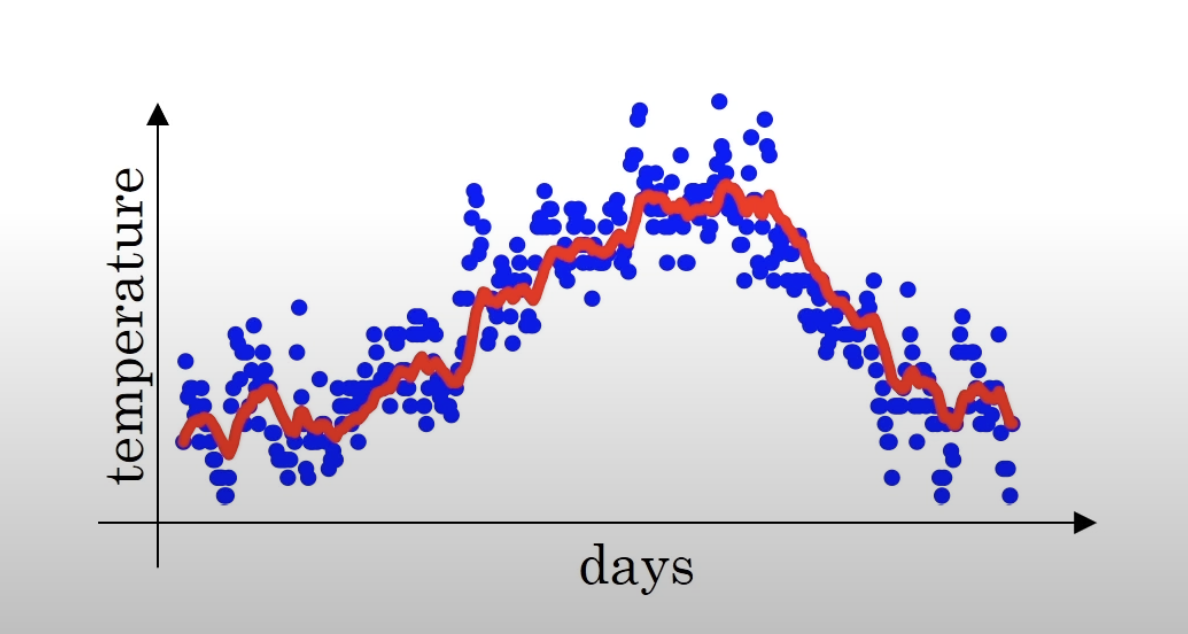
이전의 그래프 보다 트랜드를 더 잘 반영하고 있다.