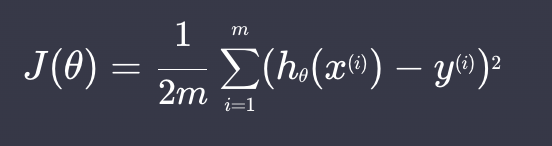정규화(Regularization)

높은 분산으로 신경망이 데이터를 과대적합하는 문제가 의심 된다면 가장 처음 시도해야 될 것은 정규화다. 보편적으로 데이터를 더 추가하는 것이 성능 향상에 도움이 되지만 데이터를 구하는 것은 비용이 듦으로 현실적인 상황에서는 정규화를 시도하는 것이 바람직하다.

L1 정규화

다항 회귀로 예시를 들기전에 다항회귀의 손실 함수는 아래와 같다 (#미분의 편의를 위해 2를 나누었다)

손실함수는 일반적으로 가설함수(예측값)를 평가하는 함수이다. 하지만 이러한 손실함수로 경사하강을 진행하면 가중치가 커져 과적합이 될 수가 있다.
그래서 L1 정규화는 가중치가 커져 과적합이 되는 것을 막기 위해 손실함수에 항을 한개 더 추가했다.

• $\lambda$: 가중치에 대한 페널티

손실함수를 이렇게 정의하면 가중치가 커질 수록 손실함수 값이 커지기 때문에, 손실함수가 커져 과적합 되는 것을 막을 수 있다.

L2 정규화

L2 정규화는 손실함수에 가중치의 절대값의 합이 아닌 제곱의 합에 대한 항을 더 해준다

손실함수를 최소화하려면 가중치와 손실함수를 둘다 줄여야 되기때문에 과적합을 예방할 수 있다.

L1, L2 정규화의 차이점

• L1 정규화: 모델에 중요하지 않다고 생각 되는 가중치을 0으로 만들어 준다
• L2 정규화: 가중치를 0으로 만들지 않고 조금씩 줄인다
  
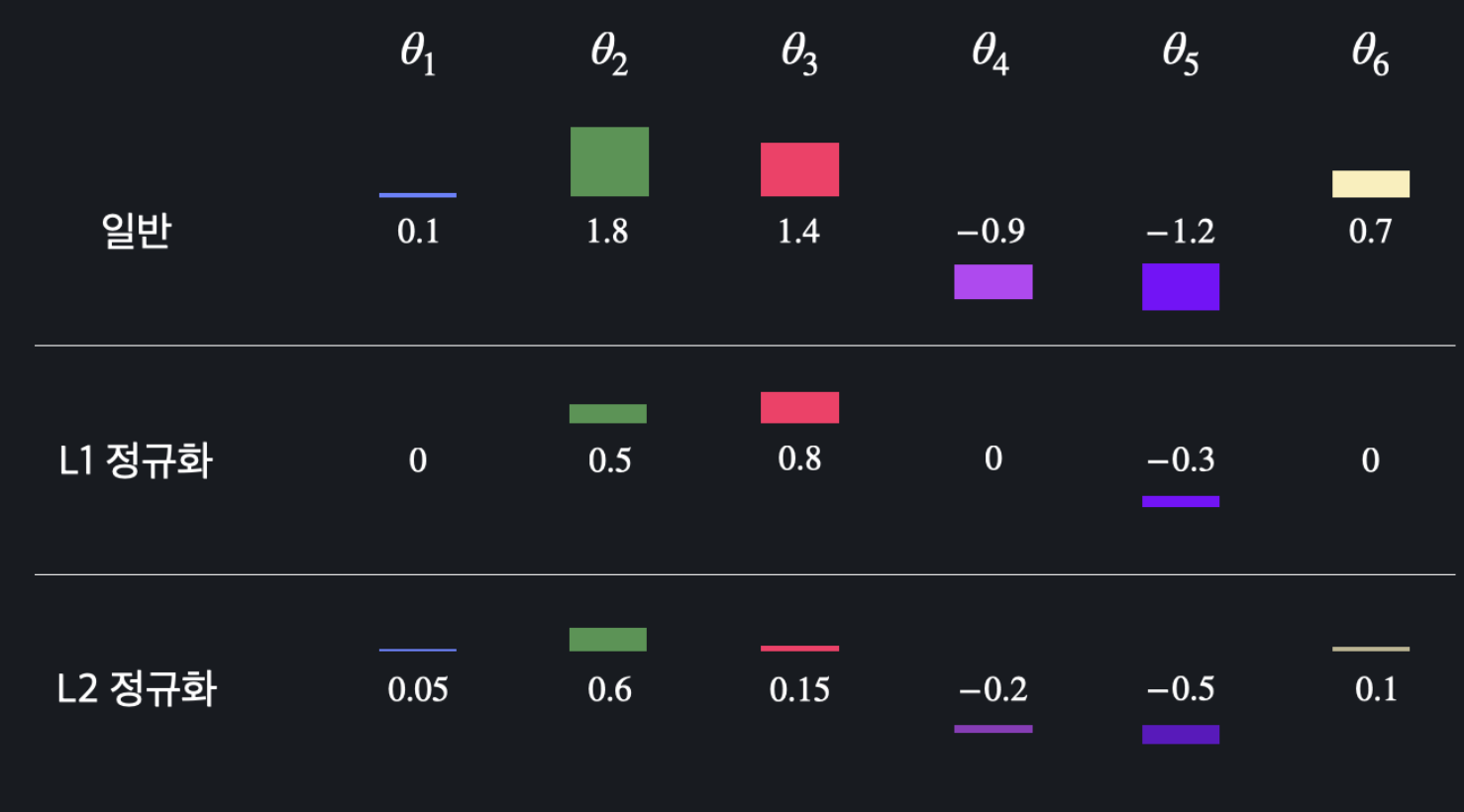
  L1 정규화에 경우 가중치가 0이되는 것들이 있으니 불필요한 feature가 많은 데이터에 사용하면 좋다. 그러나 보편적으로 L2 정규화를 많이 사용한다

Dropout 정규화

Dropout 방식은 신경망의 각각의 층에 대해 노드를 삭제하는 확률을 설정한다. 삭제할 노드를 랜덤으로 선정후 삭제된 노드와의 연결을 끊는다.
이렇게하면 더 작고 간단한 네트워크가 만들어지고 작아진 네트워크로 훈련을 진행한다.

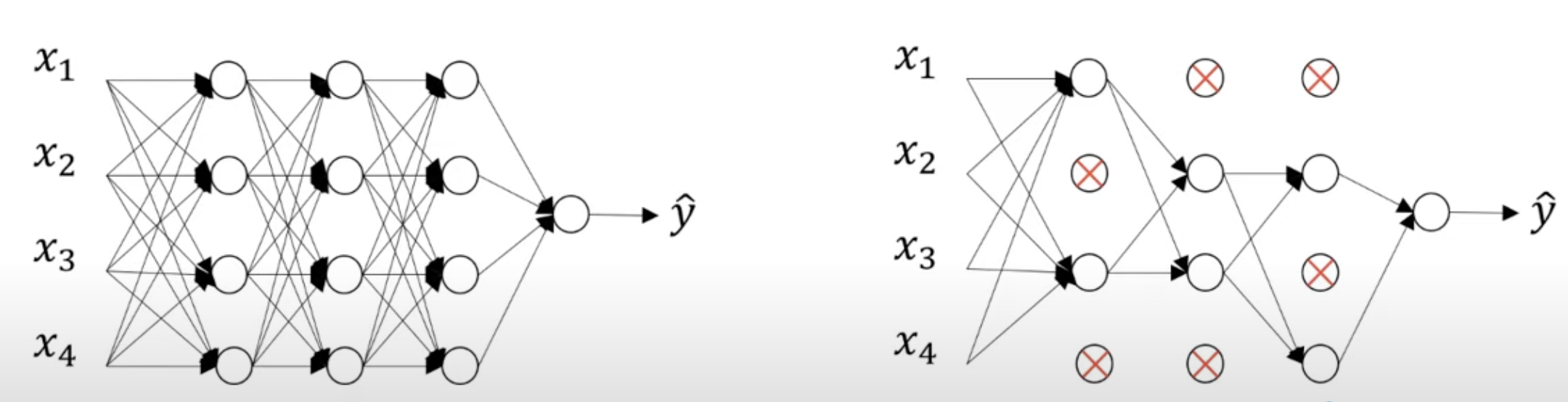
Dropout이 작동하는 원리

• 랜덤으로 노드를 삭제하기 때문에 하나의 특성에 의존하지 못하게 만듦으로 가중차를 다를 곳으로 분산 시키는 효과가 있다

Data augmentation

이미지의 경우 더 많은 훈련 데이터를 사용함으로서 과대적합을 해결 할 수 있다.
보통 이미지를 대칭 확대 왜곡 시켜서 새로운 훈련 데이터를 만든다.