
📝 회귀 분석(Regression Analysis)
하나 이상의 독립변수들이 종속변수에 미치는 영향을 추정하는 통계 기법으로
numerical data(수치형 데이터)를 이용하여 예측하는 모델이다.
y = β0 + β1X + ϵ
(y=종속변수, X=독립변수, β0=절편, β1=회귀계수, e=오차항)
🔎 자세히 알아보기
X = 독립변수, 설명변수, 예측변수, features
y = 종속변수, 반응변수, 결과변수, label, target1) Linear Regression
독립변수와 종속변수의 선형 상관 관계를 모델링하는 회귀분석 기법이다.
# Linear 모델 학습
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)단순회귀(Simple Linear Regression)
독립변수와 종속변수가 각각 한 개이며, 종속변수와 직선 관계인 회귀 모델이다.
y = β0 + β1X1
다중회귀(Multi Linear Legression)
독립변수가 2개 이상이며, 종속변수와 선형 관계인 회귀 모델이다. 설명변수들 사이에 다중공선성 문제가 발생하면 문제가 있는 변수를 제거하거나 주성분 회귀 모델을 적용하여 문제를 해결한다.
y = β0 + β1X1 + β2X2
2) Ridge(L2 Norm) Regression
정규화(regularized) 선형회귀 방법으로 선형회귀 계수에 대한 패널티(λ)라는 제약 조건을 추가함으로써 모델의 과적합을 줄여준다.
회귀계수(β)에 가중치들의 제곱의 합을 대입하여 계수가 0에 가깝게 축소시킨다.(dimension을 축소)
# Ridge 모델 학습
from sklearn.linear_model import Ridge
model = Ridge(alpha=alpha, normalize=True)
model.fit(X_train, y_train)3) Lasso(L1 Norm) Regression
정규화(regularized) 선형회귀 방법으로 회귀계수(β)에 가중치들의 절대값의 합을 대입하여 계수가 0으로 축소시킨다.(dimension을 삭제)
# Lasso 모델 학습
from sklearn.linear_model import Lasso
model = Lasso()
model.fit(X_train, y_train)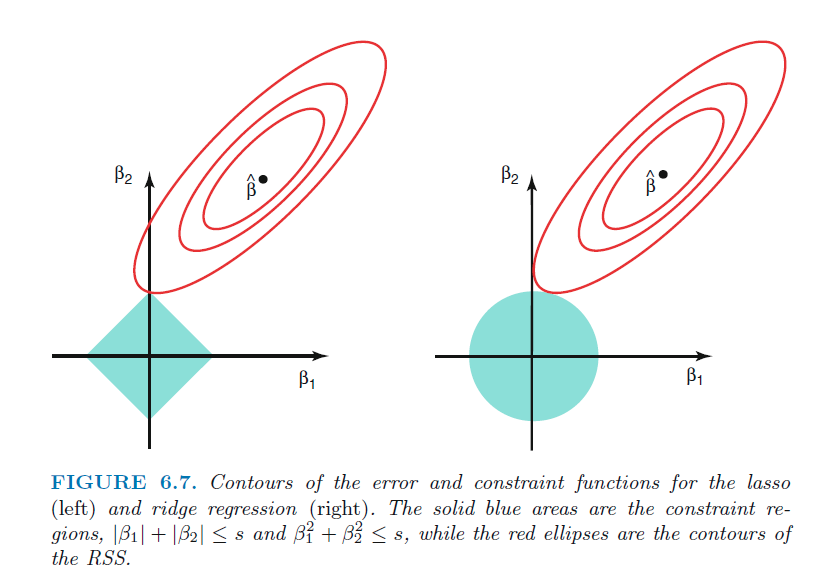
4) Elastic Net Regression
정규화(regularized) 선형회귀 방법으로 회귀계수(β)에 가중치의 절대값의 합과 제곱합을 동시에 축소시킨다.
5) Logistic Regresstion
종속 변수가 범주형 데이터이며 이진형(binary)인 회귀 모델이다.
# Logistic 모델 학습
from sklearn.linear_model import LogisticRegression
logistic = LogisticRegression()
logistic.fit(X_train, y_train)📝 용어정리
1. Tabular Data
행과 열로 구성된 표 형식의 데이터이다.
observations(행/관측점), variable(열/변수), relationships 3가지 특징이 있다.
2. 회귀선(Regression Line)
잔차 제곱들의 합인 RSS(residual sum of squares)를 최소화 하는 직선이다. 머신러닝에서 RSS는 회귀모델의 비용함수(Cost function)가 된다.
🔎 자세히 알아보기
잔차(residual): 예측값과 관측값 차이
오차(error): 모집단에서의 예측값과 관측값 차이3. 기준모델(Baseline Model)
예측 모델을 만들기 전에 직관적이면서 최소한의 성능을 나타내는 기준이 되는 모델이다.
🔎 자세히 알아보기
분류문제: 타겟의 최빈 클래스
회귀문제: 타겟의 평균값
시계열회귀문제: 이전 타임스탬프의 값4. 훈련/검증/테스트 데이터
훈련(train) 데이터: 학습을 위한 데이터 셋
검증(validation) 데이터: 최적 모델(하이퍼 파라미터)을 선택하기 위한 데이터 셋
테스트(test) 데이터: 학습된 모델의 성능 검증을 위한 데이터 셋(테스트용)
머신러닝에서는 모델이 학습에 사용하지 않은 테스트 데이터를 얼마나 잘 맞추는지가 중요하기 때문에 데이터를 훈련/검증/테스트 데이터로 나누어야 모델의 예측 성능을 제대로 평가할 수 있다.
5. 회귀계수(cofficient)
독립변수가 한 단위 변화함에 따라 종속변수에 미치는 영향력 크기이다.
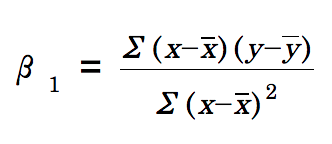
6. 최소제곱법(OLS)
잔차제곱합(RSS)를 최소화하는 가중치 벡터를 구하는 방법이다.
7. Bias–variance tradeoff
모델을 학습시킬 때 bias와 variance가 동시에 최소화될 수 없는 상충관계를 의미한다.
편향(Bias): 실제 데이터와 예측 데이터 사이의 거리
분산(Variance): 예측 데이터들 사이의 거리(흩어진 정도)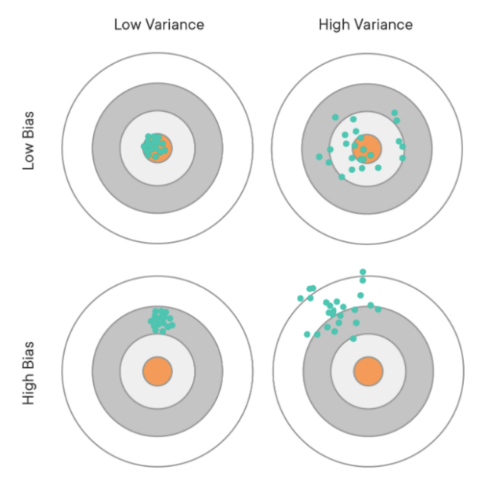
✍🏻 그래프 해석(1)
첫번째 그래프: 예측값(녹색점)들이 target(주황색점)과 거의 붙어있으므로 편향이 적고, 예측값들이 서로 가까우므로 분산이 적다.
두번째 그래프: 예측값들이 target과 가까우므로 편향이 적고, 예측값들이 서로 멀리 떨어져있으므로 분산이 크다.
세번째 그래프: 예측값들이 target과 멀리 떨어져있으므로 편향이 크고, 예측값들이 서로 가까우므로 분산이 적다.
네번째 그래프: 예측값들이 target과 멀리 떨어져있으므로 편향이 크고, 예측값들이 서로 멀리 떨어져있으므로 분산이 크다.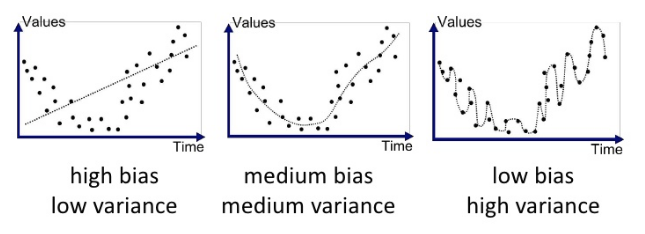
✍🏻 그래프 해석(2)
첫번째 그래프: 데이터(점)들이 모델(선)과 멀어져 있으므로 편향이 크고, 모델의 예측 데이터들은 서로 가까우므로 분산이 적다.(Underfitted)
두번째 그래프: 데이터들이 모델과 어느 정도 가까우므로 편향이 적당하고, 모델의 예측 데이터들 사이의 거리도 어느 정도 가까우므로 분산이 적당하다.(Good fit/Robust)
세번째 그래프: 데이터들이 모델과 거의 붙어있으므로 편향이 적고, 모델의 예측 데이터들은 서로 멀어져 있으므로 분산이 크다.(Overfitted)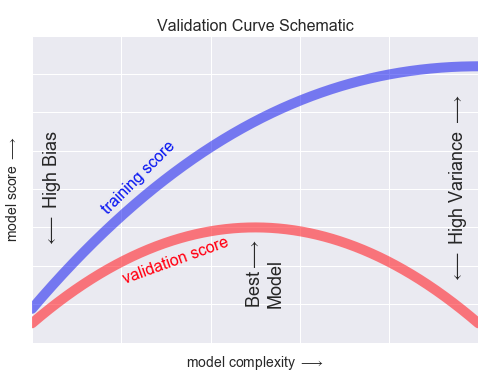
✍🏻 그래프 해석(3)
모델의 복잡성에 따른 성능 그래프이다.
모델이 복잡해질 수록 훈련데이터 성능은 계속 증가하는데,
검증데이터 성능은 어느정도 증가하다가 증가세가 멈추고 오히려 낮아지는 지점이 있다.
이 지점을 '과적합'이 일어나는 시점이라고 한다.Code Review
import pandas as pd
from sklearn.linear_model import LinearRegression
# 데이터셋 만들기
data = pd.DataFrame({'height': [160, 161, 165, 173, 171],
'weight': [55, 57, 60, 68, 65]})
# X: 특성들의 테이블, y: 타겟 벡터
target = 'weight'
feature = 'height'
y_train = data[target]
X_train = data[[feature]]
# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)
# 계수(coefficient)
model.coef_
# 절편(intercept)
model.intercept_
# 예측
n = 180
X_test = [[n]]
y_pred = model.predict(X_test)
print('키가',n,'일 때 몸무게: ', y_pred)