Binary Tree

이진 트리

• 각 노드가 최대 두 개의 자식을 갖는 트리

• 모든 트리가 이진트리는 아니다.

• 이진 트리 순회

  • 중위 순회(in-order traversal)

    

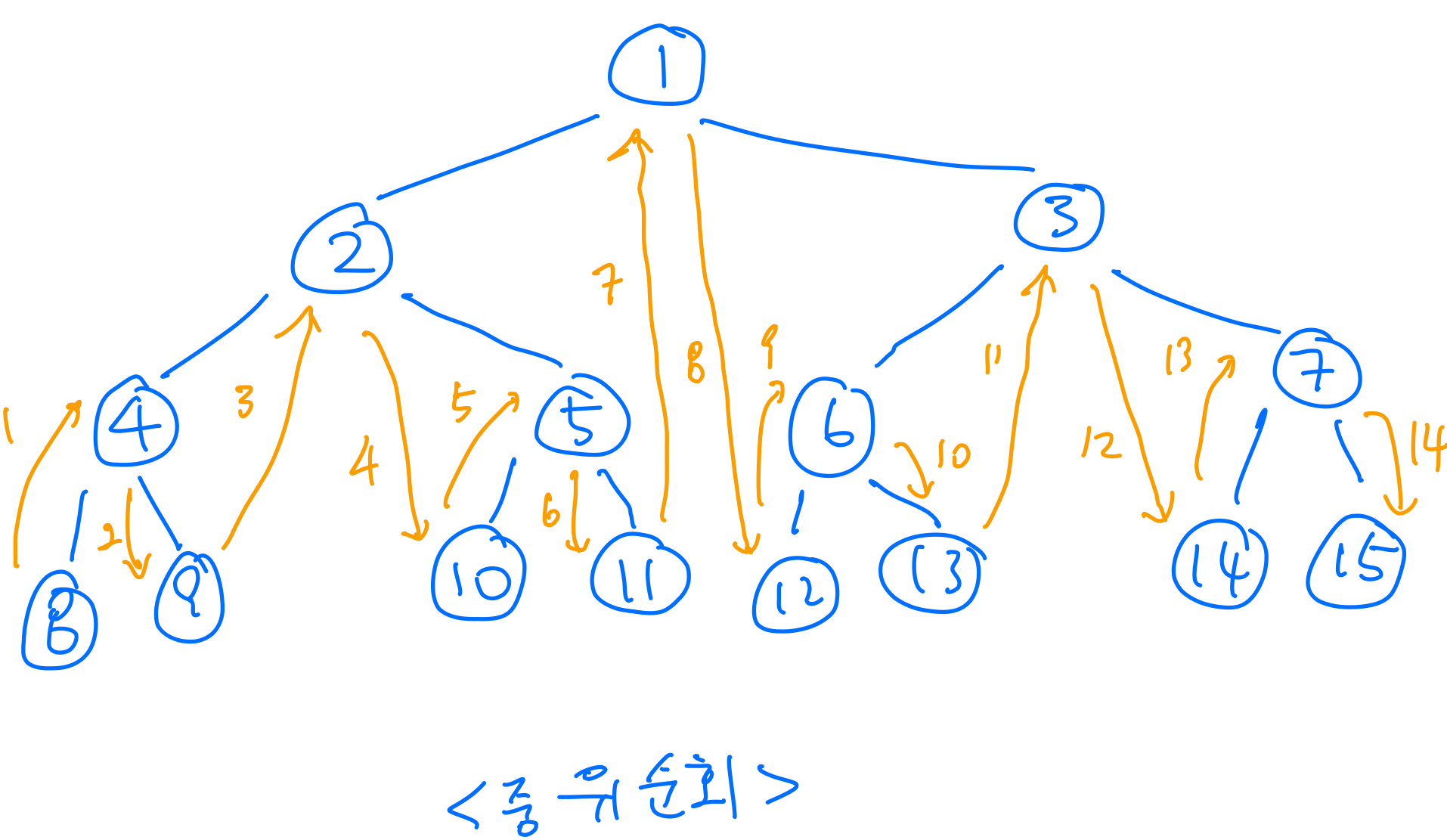
    void in_order_traversal(tree_node node)
    {
    	if (node != NULL)
    	{
    		in_order_traversal(node->left);
    		visit(node);
    		in_order_traversal(node->right);
    	}
    }

  • 전위 순휘(pre-order traversal)

    

    void pre_order_traversal(tree_node node)
    {
    	if (node != NULL)
    	{
    		visit(node);
    		pre_order_traversal(node->left);
    		pre_order_traversal(node->right);
    	}
    }

  • 후위 순회 (post-order traversal)

    

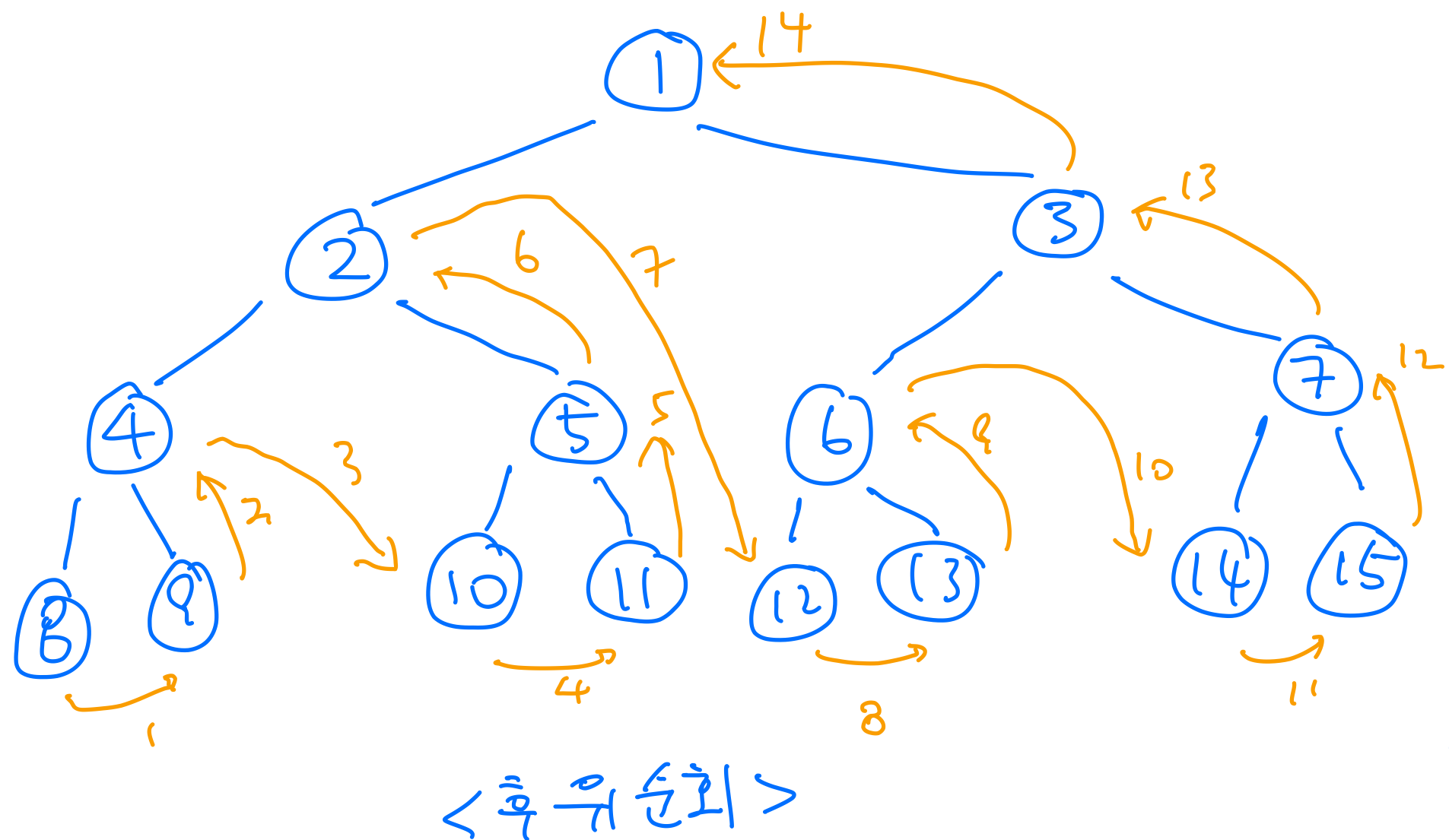
    void post_order_traversal(tree_node node)
    {
    	if (node != NULL)
    	{
    		post_order_traversal(node->left);
    		post_order_traversal(node->right);
    		visit(node);
    	}
    }

이진 트리 vs 이진 탐색 트리

• 이진 탐색 트리 (Binary Search Tree)
  • 모든 노드가 아래와 같은 특정 순서를 따르는 속성이 있는 이진 트리
  • 모든 왼쪽 자식들 ≤ n < 모든 오른쪽 자식들

균형 트리 vs 비 균형 트리

• 균형 트리
  • O(logN) 시간에 insert와 find를 할 수 있을 정도로 균형이 잘 잡혀 있는 트리
  • 레드-블랙 트리, AVL 트리

완전 이진 트리 vs 전 이진 트리 vs 포화 이진 트리

• 완전 이진 트리 (Complete BT)

  

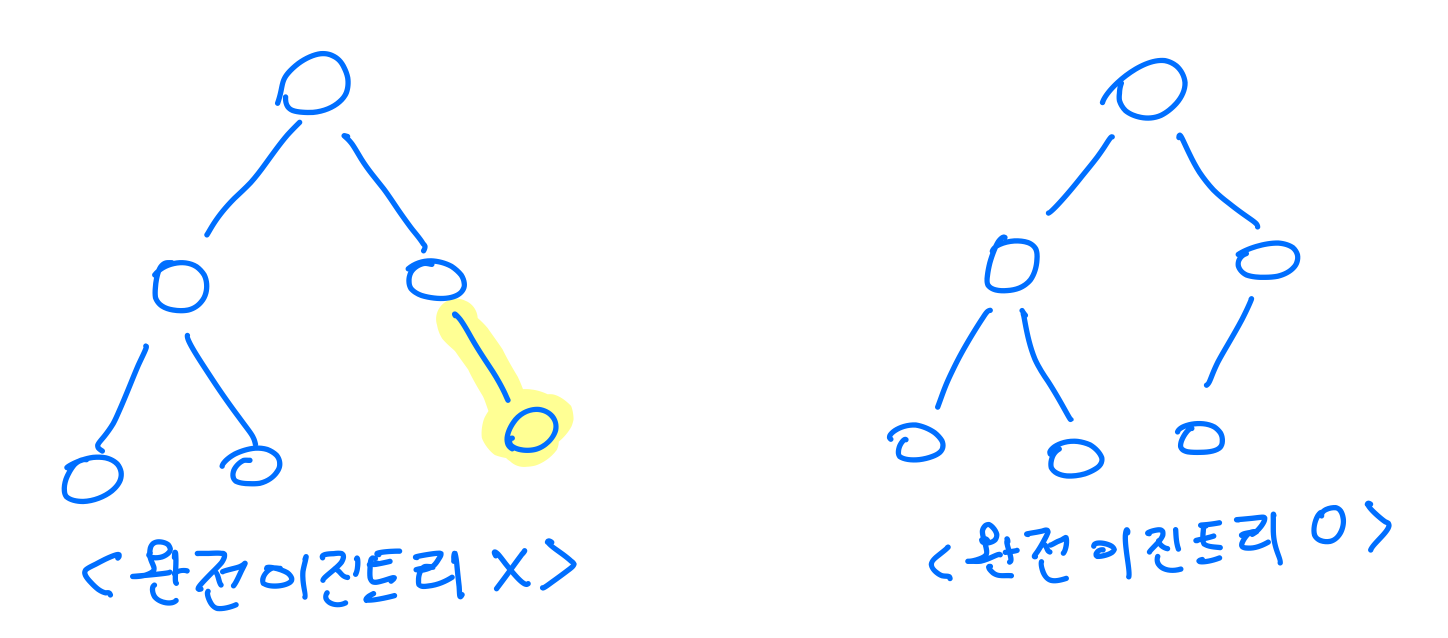
  • 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리. 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
  • 마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
  • 마지막 레벨 h에서는 1개 ~ 2h -1개의 노드를 가질 수 있다.
  • 또 다른 정의는 가장 오른쪽의 리프 노드가 제거된 포화 이진 트리다.
  • 완전 이진 트리는 배열을 사용하여 효율적으로 표현이 가능하다.

• 전 이진 트리 (Full BT / Strictly BT)

  

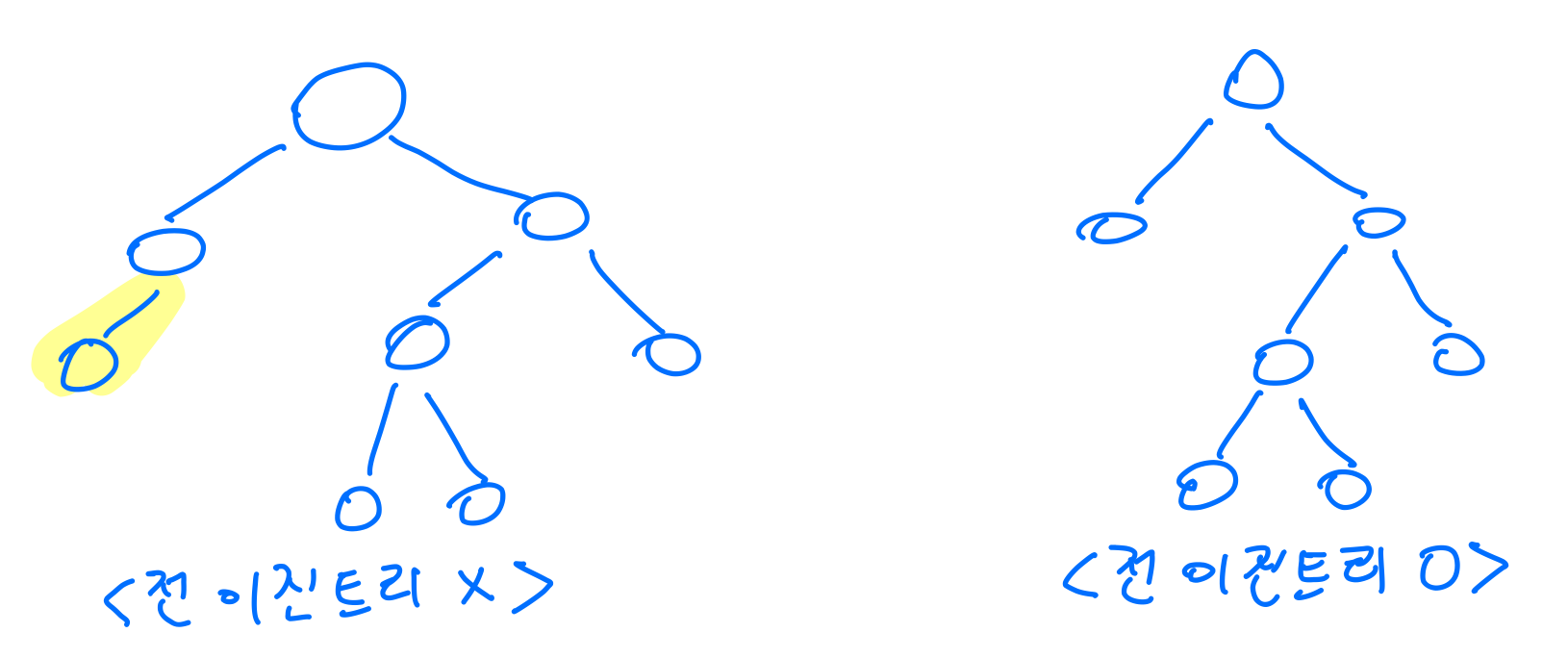
  • 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

• 포화 이진 트리 (Perfect BT)

  

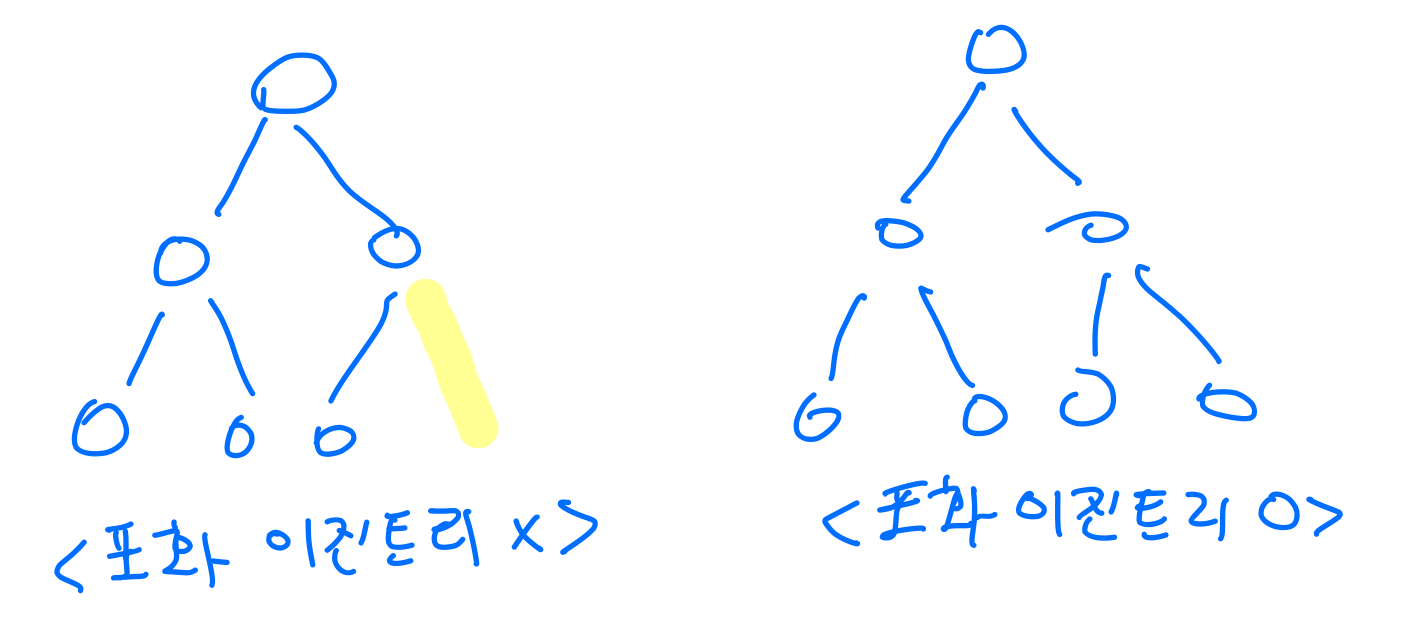
  • 전 이진트리이면서 완전 이진트리인 경우
  • 모든 리프 노드는 같은 높이에 있어야 하며, 마지막 레벨에서 노드의 개수가 최대가 되어야 한다.
  • 모든 내부 노드가 두 개의 자식 노드를 가진다.
  • 모든 말단 노드가 동일한 깊이 / 레벨을 갖는다.
  • 노드의 개수가 정확하게 (2^h - 1)개이다. (h: 트리의 높이)