부스트캠프 week1 추가학습 Gradient Vanishing, Exploding

Dae Hee Lee·2021년 8월 8일

BoostCamp

목록 보기

8/22

기울기 소실(Gradient Vanishing)

이 내용에 대한 지식이 제대로 머리속에 정리되지 않아 한 번 정리하는 시간을 가지려 한다. 기울기 소실은 역전파 과정에서 입력층으로 갈수록 Gradient가 점차적으로 작아지는 현상을 말한다.

활성화 함수로 자주 사용되는 Sigmoid와 같은 여러 함수의 특성이, 미분해서 가지는 값들이 1보다 작아 계속해서 곱해나가면 0에 가까이 되고, 이는 가중치 업데이트가 제대로 이루어지지 않게 된다. 이렇게 가중치들이 업데이트가 제대로 되지 않으면 최적의 모델을 찾는 데 어려움을 겪게 된다. 반대의 경우로는 기울기 폭주(Gradient Exploding) 이 있는데, 기울기가 점차 커지더니 가중치들이 비정상적으로 큰 값이 되면서 발산하는 형태이며, RNN에서 발생할 수 있다.

Gradient Vanishing 해결 - ReLU
따라서 위와 같은 문제를 해결하기 위해 ReLU, 또는 ReLU의 변형 함수를 Activation Function으로 활용하게 된다.

Gradient Exploding 해결 - Gradient Clipping
Gradient Clipping은 기울기 값을 자른다는 의미로, 임계값을 설정해 기울기가 임계값을 넘지 않도록 임계치만큼 크기를 감소시키게 된다.

가중치 초기화

가중치 행렬 W를 초기화(Initialization)하는 방법으로, 가중치 행렬의 분포를 균등 분포(Uniform Distribution)를 사용하여 초기화하는 방법이다. 자세한 내용은 논문을 링크걸어놓도록 하겠다.
1) 세이비어 초기화(Xavier Initialization)
2) HE Initialization

배치 정규화

위의 방법으로 기울기 소실 문제를 어느정도 해결할 수 있지만, 훈련 중에 언제든지 문제가 다시 발생할 수 있다. 따라서 또 다른 기울기 소실 및 폭주 예방법으로 배치 정규화를 사용한다. 간단하게 이야기하면 NN의 각 층에 들어가는 입력을 평균과 분산으로 정규화하여 학습을 효율적으로 하는 방식이다.

1)내부 공변량 변화(Internal Covariate Shift)
배치 정규화를 이해하기 위한 사전 지식으로 내부 공변량 변화를 이해해야 한다. Internal Covariate Shift란 학습 과정에서 층 별로 입력 데이터 분포가 달라지는 현상을 말한다. 이전 층들의 학습에 의해 이전 층의 가중치가 변하게 되면, 현재 층에 전달되는 입력 데이터의 분포가 현재 층이 학습했던 시점의 분포와 차이가 발생하게 된다.

2)배치 정규화(Batch Normalization)
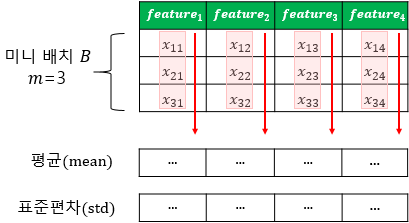
배치 정규화는 말 그대로 한 번에 들어오는 배치 단위로 정규화를 진행하는 것을 의미한다. 각 층에서 활성화 함수를 통과하기 전에 수행되며, 입력 데이터의 평균을 0으로 옮기고 정규화를 진행한다. 정규화된 데이터에 대해서는 스케일과 시프트를 수행한다. 두 개의 매개변수 $\gamma$ , $\beta$ 를 사용하는데 $\gamma$ 는 스케일을 위해 사용하고, $\beta$ 는 시프트를 하는 것에 사용하며 다음 레이어에 일정한 범위의 값들만 전달되게 한다. 아래 식을 통해 쉽게 이해할 수 있다.

$m$ 은 미니 배치에 있는 샘플의 수
$\mu_{B}$ 는 미니 배치 $B$ 에 대한 평균
$\sigma_{B}$ 는 미니 배치 $B$ 에 대한 표준편차
$\hat{x}^{(i)}$ 은 평균이 0이고 정규화 된 입력 데이터
$\varepsilon$ 은 $\sigma^{2}$ 가 0 일 때, 분모가 0이 되는 것을 막는 작은 양수. 보편적으로 $10^{-5}$
$\gamma$ 는 정규화 된 데이터에 대한 스케일 매개변수로 학습 대상 $\beta$ 는 정규화 된 데이터에 대한 시프트 매개변수로 학습 대상
$y^{(i)}$ 는 스케일과 시프트를 통해 조정한 $B N$ 의 최종 결과

2-1) 배치 정규화의 특징

배치 정규화를 사용하면 시그모이드 함수나 하이퍼볼릭탄젠트 함수를 사용하더라도 기울기 소실 문제가 크게 개선된다.
가중치 초기화에 훨씬 덜 민감해진다.
훨씬 큰 학습률을 사용할 수 있어 학습 속도를 개선시킨다.
미니 배치마다 평균과 표준편차를 계산하여 사용하므로 훈련 데이터에 일종의 잡음 주입의 부수 효과로 과적합을 방지하는 효과도 낸다. 다시 말해, 마치 드롭아웃과 비슷한 효과를 낸다. 물론, 드롭 아웃과 함께 사용하는 것이 좋다.
배치 정규화는 모델을 복잡하게 하며, 추가 계산을 하는 것이므로 테스트 데이터에 대한 예측 시에 실행 시간이 느려진다. 그래서 서비스 속도를 고려하는 관점에서는 배치 정규화가 꼭 필요한지 고민이 필요하다.
배치 정규화의 효과는 굉장하지만 내부 공변량 변화때문은 아니라는 논문도 있다. : https://arxiv.org/pdf/1805.11604.pdf

3) 배치 정규화의 한계

미니 배치 크기에 의존적이다.
배치 정규화는 너무 작은 배치 크기에서는 잘 동작하지 않을 수 있다. 단적으로 배치 크기를 1로 하게되면 분산은 0이 된다. 작은 미니 배치에서는 배치 정규화의 효과가 극단적으로 작용되어 훈련에 악영향을 줄 수 있다. 배치 정규화를 적용할때는 작은 미니 배치보다는 크기가 어느정도 되는 미니 배치에서 하는 것이 좋다. 이처럼 배치 정규화는 배치 크기에 의존적인 면이 있다.
RNN에 적용하기 어렵다.
RNN은 각 시점(time step)마다 다른 통계치를 가진다. 이는 RNN에 배치 정규화를 적용하는 것을 어렵게 만든다. RNN에서 배치 정규화를 적용하기 위한 몇 가지 논문이 제시되어 있지만 여기서는 다루지 않을 것이다. 대신 배치 크기에도 의존적이지 않으며 RNN에도 적용하는 것이 수월한 층 정규화(layer normalization)라는 방법을 소개하고자 한다.