LaTex수식 관련:
- 수식 변환 프로그램 설치(Mathpix)
설치 후 원하는 수식 스크린샷을 활용하여 LaTex로 변환할 수 있다.
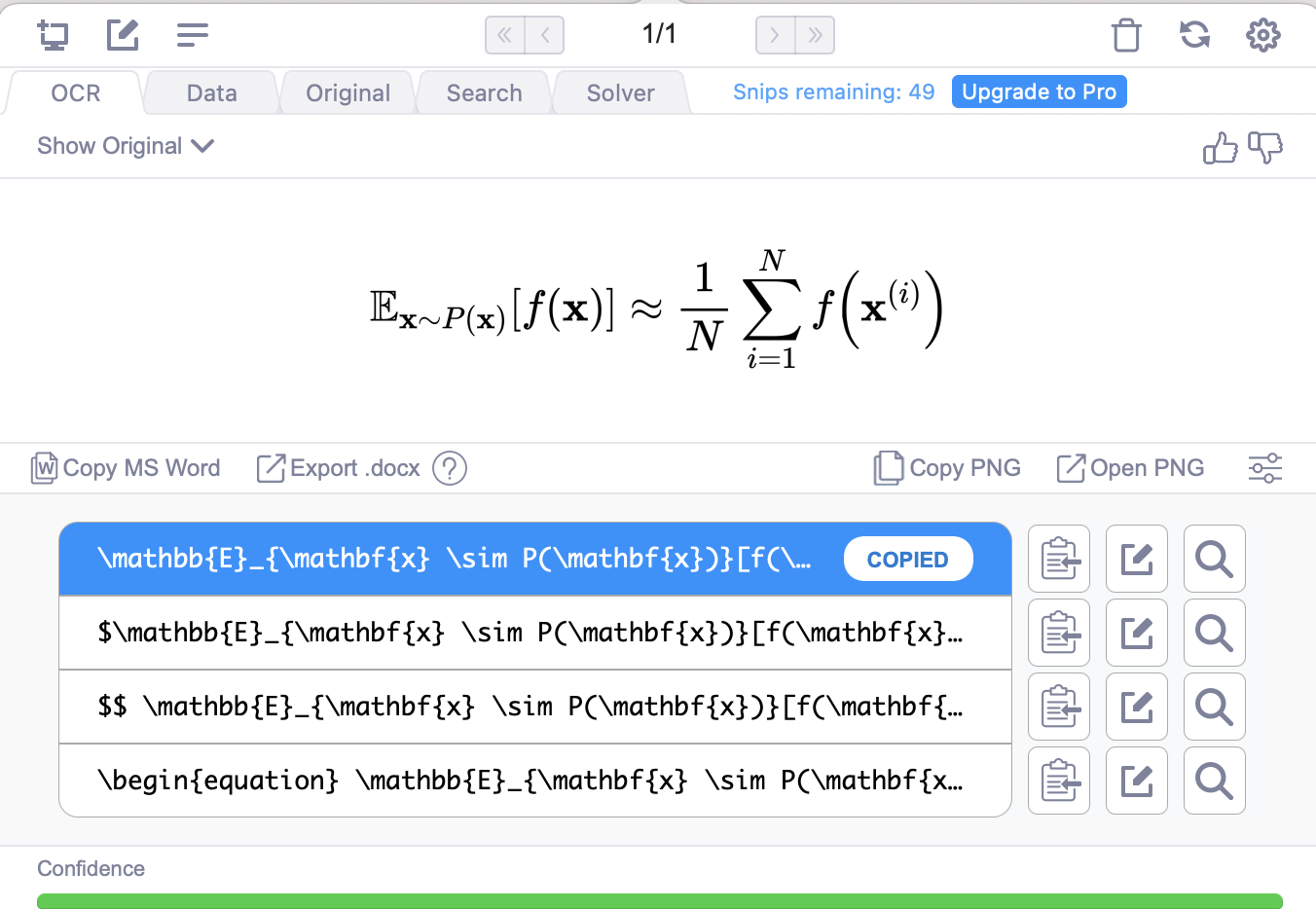
확률론
딥러닝에 확률론이 왜 필요할까?
딥러닝 : 확률론 기반의 기계학습 이론에 바탕
- 손실함수(Loss Function)은 데이터 공간을 통계적으로 해석해서 유도
- 회귀 분석에서 손실함수로 사용되는 L2 norm은 예측 오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도
- 분류 문제의 Cross Entropy는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도
- 분산 및 불확실성을 최소화하기 위해 이를 측정하는 방법을 알아야 함
조건부확률과 기계학습
- 딥러닝은 MLP를 이용해서 데이터로부터 특징 패턴을 추출함
- 분류에서는 softmax함수가 조건부 확률을 계산하고, 회귀에서는 조건부 기대값을 추정
몬테카를로 샘플링
- 이산형이든 연속형이든 상관없지만 독립적이어야함
- 확률 분포를 모르는 경우가 대부분으므로, 데이터를 이용하여 기대값을 계산하는 방법
- Uniform Distribution의 x로 샘플링하여 평균을 구하는 방법임.
아래는 몬테카를로 샘플링을 이용하여 원주율을 근사하는 방법이다.
import numpy as np
def mc_int(fun,low,high,sample_size=100,repeat=10):
int_len = np.abs(high-low)
stat = []
for _ in range(repeat):
x = np.random.uniform(low,high,size=sample_size)
fun_x = fun(x)
int_val = int_len * np.mean(fun_x)
stat.append(int_val)
return round(np.mean(stat),5), round(np.std(stat),5)
def f_x(x):
return np.sqrt(1-x**2)
print(2*mc_int(f_x,low=-1,high=1, sample_size=100000, repeat=100)[0])통계학
통계적 모델링은 적절한 가정 위에서 확률분포를 추정(Inference) 하는 것이 목표이며, 기계 학습과 통계학이 공통적으로 추구하는 목표이다. 따라서 유한 개의 데이터를 관찰하여 근사적으로 확률 분포를 추정할 수 있다.
-
데이터가 특정 확률 분포를 따른다고 가정한 후, 그 분포를 결정하는 Parameter(모수)를 추정하는 방법을 Parametric(모수적 방법론)이라고 한다. 특정 확률 분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌먄 비모수 방법론이라고 부른다.
-
다음은 확률분포를 가정하는 대표적인 예이다.
- 데이터가 2개의 값만 가질 때 : 베르누이 분포
- 데이터가 n개의 이산적인 값을 가질 경우 : 카테고리 분포
- 데이터가 [0,1]사이의 값을 가질 경우 : 베타 분포
- 데이터가 0 이상의 값을 가지는 경우 : 감마분포, 로그정규분포
- 데이터가 실수 집합 전체에서 값을 가지는 경우 : 정규분포, 라플라스분포
- 데이터를 관찰한 후에 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙
- 모수 추정 후에는 적절한 방식으로 검증을 해야 한다.
정규분포 모수 추정
데이터로 모수를 추정하는 대표적인 예는 정규분포의 모수 추정이다.
정규분포는 ()의 모수를 가지며, 각각 평균과 분산이다. 우리는 임의의 표본을 추출하였을 때 표본 평균의 기대값을 모집단의 평균으로 추정할 수 있고, 보통의 분산 공식과 달리 N-1로 나누어주어 구한 표본 분산의 기대값을 통해 모집단의 분산을 추정할 수 있다. 참고 - 표본 분산은 로 나누어주는 이유 수식으로 증명(중심극한정리 이용)
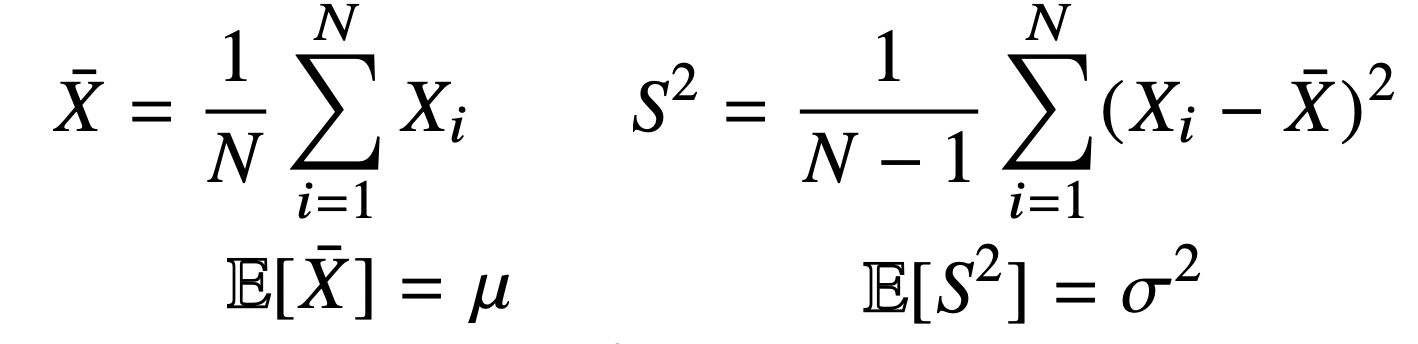
이런 통계량의 확률 분포를 Sampling distribution이라고 하고, 이는 표본들의 분포를 의미하는 Sample Distribution과는 차이가 있다.
그리고 표본평균의 은 N이 커질수록 정규분포 을 따르는 것이 통계적으로 증명되어있다. 참고 - 중심극한정리
표본평균, 표본분산도 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 필요하다. 가장 가능성이 높은 모수를 추정하는 방법 중 하나가 최대가능도 추정법이다.
최대가능도방법 (最大可能度方法, 영어: maximum likelihood method) 또는 최대우도법(最大尤度法)은 어떤 확률변수에서 표집한 값들을 토대로 그 확률변수의 모수를 구하는 방법이다. 어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도를 최대로 만드는 모수를 선택하는 방법이다. 점추정 방식에 속한다.
쉽게 말하면, 우리는 어떠한 확률 변수를 가지는 상황에서 결과값들을 모으게 된다. 이 때, 확률 변수란 말 그대로 그 상황이 발생할 확률을 변수로 표현한 것이다.
이 때 Likelihood는 번의 시행이 각각 이 나올 가능성(확률)이다. 즉, 각 확률변수에 대해서 확률 밀도(질량) 함수가 라면, Likelihood값은 이다. 만약 각 확률변수들이 독립적이고 같은 확률 분포를 가지고 있다면 으로 표현이 가능할 것이고, 여기에 를 취해 단조 증가함수로 만들어 계산을 쉽게 하기도 한다.
확률변수들이 독립적이다 = 데이터 행렬 X의 행 벡터가 독립적이다.

왜 로그가능도를 사용할까?
- 로그가능도를 통해 찾은 MLE는 가능도를 최적화하는 MLE이다. 하지만 만약 수 억개 이상의 아주 많은 데이터라면 컴퓨터에서는 곱셈 연산이 어려워집니다. 하지만 로그가능도를 이용해서 덧셈 연산으로 계산할 수 있기 때문에 연산이 가능해집니다.
- 또한 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그가능도를 사용하면 연산 복잡도를 에서 으로 줄일 수 있습니다.
- 경사하강법에서는 음의 로그가능도를 통해 최적화를 합니다.
이 때, 이러한 함수들에 영향을 주는 모수가 존재한다. Gaussian Distribution에서 가 그럴 것이다. 우리는 이 모수들을 통틀어 로 표현할 수 있다. 따라서
로 표현할 수 있다. 이 때, 우리는 이 가능도를 최대로 만드는 가 구하고 싶은 것이다. 즉 이렇게 Likelihood를 최대로 만드는 값을 라 하고, 위 내용을 수식으로 적으면
가 된다. 이제 우리는 가능도함수를 , 즉 데이터에 관한 함수로 보는 것이 아니라 , 즉 모수에 대한 함수로 표현하는 것이다. 데이터는 주어져있는 상태이고, 여기서 모수를 변형시켰을 때마다 값이 바뀌는 함수이다.
즉 가능도함수란 를 가지는 분포가 데이터 를 가질 가능성을 나타내는 지표이다. 따라서 로 표현할 수도 있다.
이러한 값을 찾기 위해서는 간단하게 말하면 미분해서 0이되는 지점을 찾는 것이다. Gradient Descent에서와 같이 Learning Rate와 Loss Function의 Gradient의 곱을 계속해서 빼주는 형식으로 업데이트를 하는 것이다.
기계학습에서도 가중치를 표현했을 때 분류문제에서 소프트맥스 벡터는 카테고리분포의 모수를 모델링하는 것이다.
원핫벡터로 표현한 정답레이블 y를 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있다.

확률분포의 거리를 구해보자
기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도한다.
데이터공간에 두 개의 확률 분포 P,Q가 있을 때, 두 확률분포 사이의 거리를 계산하는 방법은 다음과 같다.
- 총변동 거리(TV)
- 쿨백-라이블러 발산(KL)
- 바슈타인 거리(WD)
쿨백-라이블러 발산
크로스 엔트로피와 엔트로피로 표현할 수 있다.
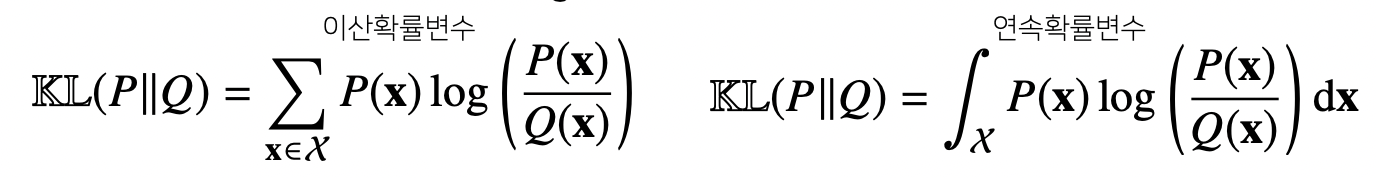

두개의 확률분포의 거리를 최소화시킨다는 것과 데이터로부터 목적 확률 분포에 최적화된 모수를 구하는 것과 동일하다.
이 블로그에서 수식적으로 크로스엔트로피가 딥러닝에서 왜 사용되는지를 잘 가르쳐주고 있다.
이렇게 MLE 를 Machine Learning을 활용해서 찾아내게 되면 주어진 데이터를 가장 잘 설명하는 확률 분포 함수를 찾으려고 하다보니, Overfitting의 가능성이 매우 높다. 이 과적합을 최소화하기 위해서는 Training Set와 Test Set으로 분리할 때, 일부를 Validation Set으로 만들어 검증을 실시해주어야 한다.
실제로 학습을 진행할 때, loss값과 val_loss값을 비교할 수 있는데, loss값은 epoch수가 커질 수록 계속 작아지지만, val_loss값은 일정 수준 떨어지다가 다시 올라가는 현상을 볼 수 있다. 따라서 val_loss값이 최소가 되는 값을 찾는 것이 중요하다고 할 수 있다.
이 외에도 오버피팅을 막기 위해서는
- 많은 데이터
- 적은 Feature 수
- Regularization(규제)
여기서 Regularization의 방법으로는 다음과 같은 것들이 있다.
- Early Stopping :
Val_loss값이 더이상 낮아지지 않을 때 Stop - Reducing Network Size :
NN 학습 양 줄일 수 있음 - Weight Decay :
NN 파라미터의 크기를 제한 - Dropout
- Batch Normalization
