CNN(Convolutional Neural Network)

Convolution 연산은 MLP와 다르게 커널을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.

입력 벡터를 모두 활용하는 것이 아니라 커널 사이즈만큼 움직여가면서 계산하는 것이며, MLP의 가중치 행렬은 i에 따라 변하는 반면 Convolution연산은 고정된 커널을 움직여가며 계산하게 되어 파라미터 사이즈를 줄이는 등의 효과가 있다.

활성화 함수를 제외한 Convolution연산도 선형 변환에 속한다.

Convolution 연산 이해하기

수학적 의미는 신호(signal)을 커널을 이용해 국소적으로 증폭, 또는 감소시켜 정보를 추출 또는 필터링 하는 것이다.

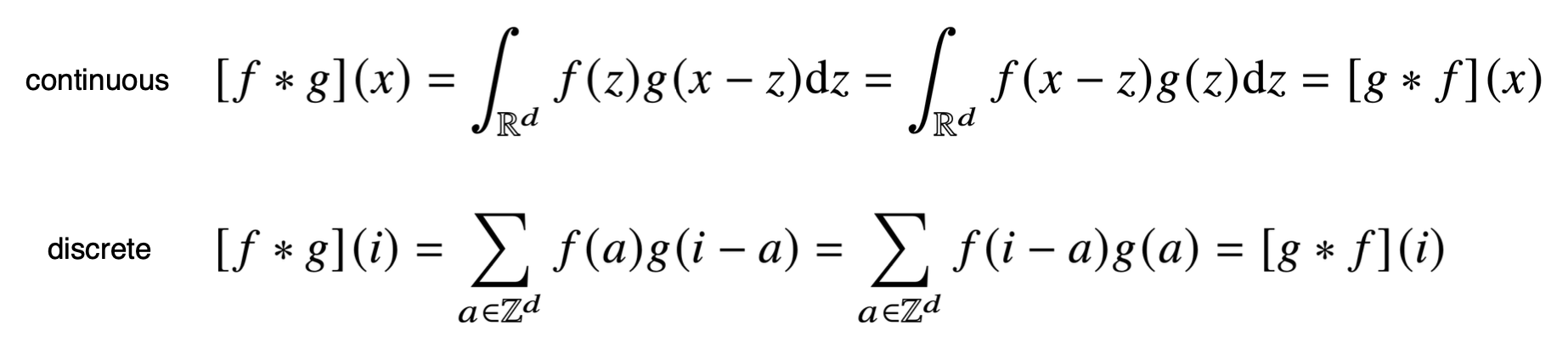
위의 수식에서 Signal, Kernel이 f,g로 표현되어 보통 kernel의 경우 함수에서 $f(z), g(a)$ 등으로 표현되는 형태이다.

CNN에서는 엄밀히 말해서 convolution보다 가운데 signal 안의 부호가 +인 cross-correlation이라 부른다. 역사적으로는 Convolution이라고 부른다.

커널은 정의역 내에서 움직여도 변하지 않고(Translation invariant) 주어진 신호에 국소적(local)으로 적용한다.

• 음성이나 텍스트는 1차원 Convolution, 흑백영상과 컬러 영상은 각각 2차원,3차원의 Convolution을 사용하며 차원이 올라가도 Kernel은 변하지 않는다.

2D-Conv 연산은 커널을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.
입력 크기를 (H,W), 커널 크기를 ($K_H$$K_W$),출력 크기를 ($O_H$$O_W$)라 하면 출력 크기는 다음과 같이 계산될 수 있다.

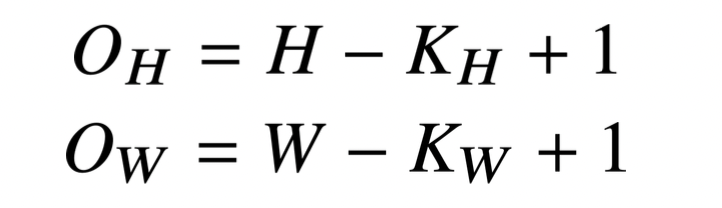
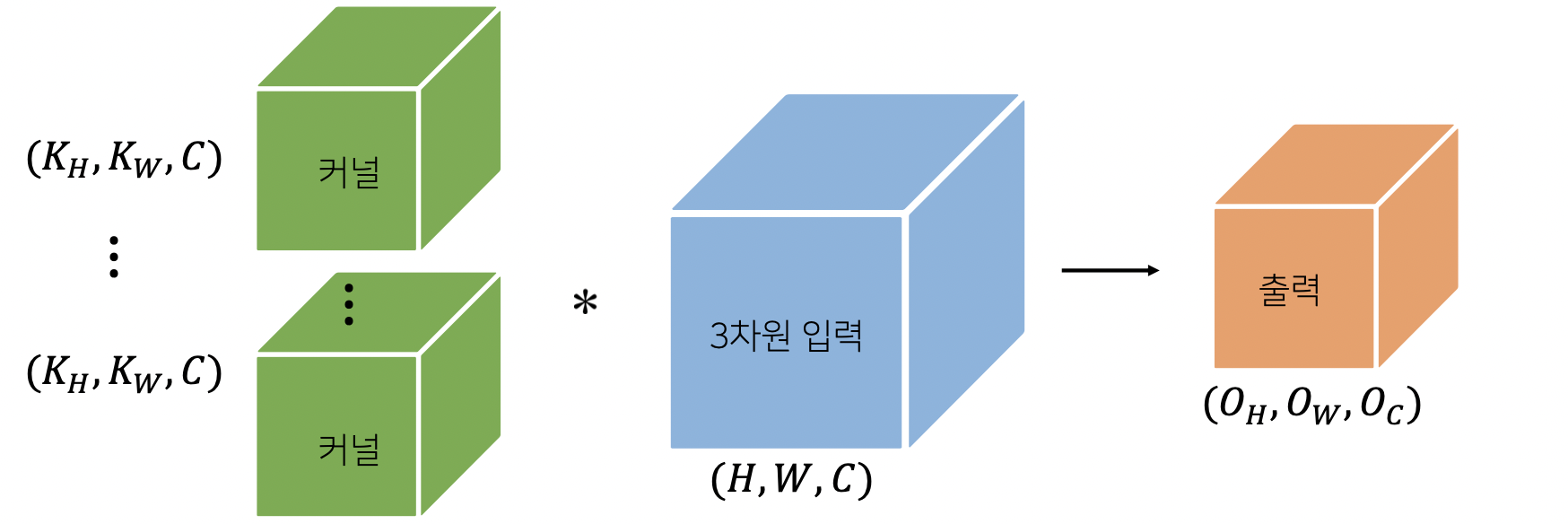
• 채널이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다고 생각하면 된다.(각각의 채널마다 Convolution 수행) 3차원부터는 행렬이 아닌 텐서라고 부른다.

즉, 2차원 커널과 입력 데이터에 채널 차원을 추가한 3차원 데이터로 바꾼다면 커널과 입력은 같은 채널값을 가지게 되고, 출력 채널은 1일 것이다.

출력의 채널을 여러개 만들고싶다면 커널의 수를 $O_C$개 만큼 늘려서 출력 채널 값을 $O_C$로 만들고 이러한 방식이 기본적인 CNN의 구조라고 볼 수 있다.

Convolution 연산의 역전파

Convolution역시 선형 변환이고, MLP의 역전파와 동일한 방식이지만 조금 다른 점이 있다.

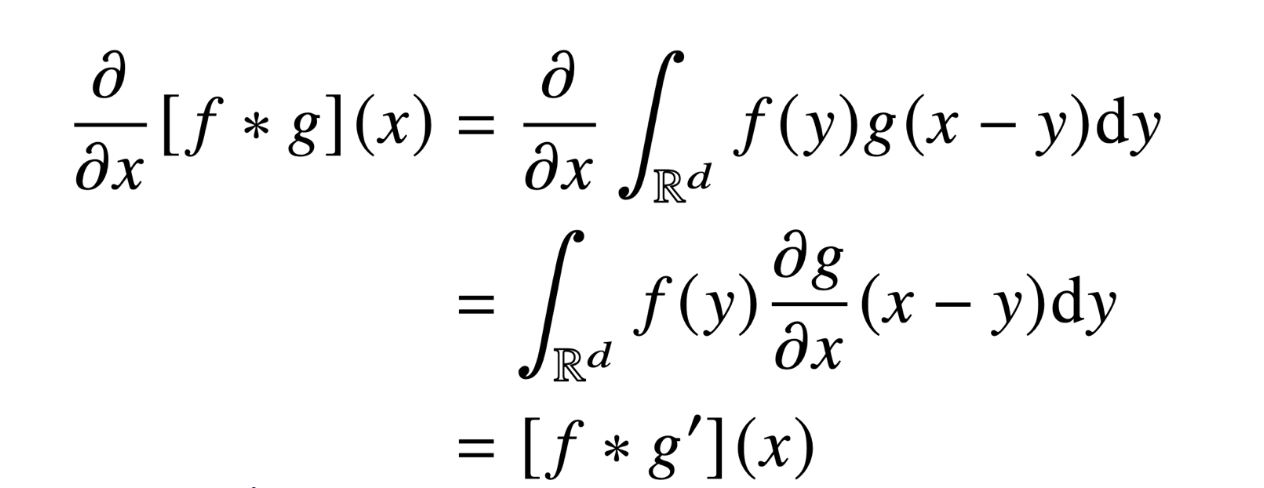
즉, convolution을 미분해도 convolution이 남아있는 모습을 볼 수 있다.

RNN(Recurrent Neural Network)

시퀀스 데이터

순차적으로 들어오는 데이터인 소리, 문자열, 주가 등의 데이터를 시퀀스 데이터로 분류한다. 또, 시계열 데이터는 시간 순서에 따라 나열된 데이터로 시퀀스 데이터이다.

시퀀스 데이터는 IID(Independent Identical Distribution) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다.

개가 사람을 물었다.
사람이 개를 물었다.

따라서, 순차적으로 들어오는 데이터를 어떻게 처리해야할까?

이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해서는 조건부확률을 이용한다.
$P(X_1, ... ,X_t) = P(X_t|X1,...,X_{t-1})\times P(X_{t-1}|X1,...,X_{t-2}) \times ...$

$X_t ~ P(X_t|X_{t-1},...,X_1)$

하지만 시퀀스 데이터는 반드시 모든 과거의 정보를 필요로하는 것은 아니다. 예를 들면 주가 예측이라면 최근 5년정도로 생각하는 등 최근의 데이터로만 필요할 수도 있다. Truncation하는 것도 데이터 처리의 한 방법이 될 것이다.

이러한 특징을 가진 시퀀스 데이터를 다루기 위해서는 가변적인 데이터를 다룰 수 있는 모델이 필요하다. 하지만 고정된 길이만큼의 시퀀스만 사용하는 경우는 AR(자기회귀)모델이라고 부른다.

특히, Latent AR(잠재 자기회귀) 모델이 RNN의 기본 모델인데, 바로 직전 정보를 제외한 정보들을 $H_t$로 놓고 인코딩하는 방법이다. 이러한 모델은 모든 데이터를 활용할 수도 있고, 가변적 길이를 고정시킬 수 있다는 장점이 있다. 그리고 여기서 과거의 정보들의 잠재변수들을 어떻게 인코딩할지에 대한 결과물이 바로 RNN이다. 잠재변수 $H_t$를 이전 잠재변수를 가지고 예측하는 방법이다.

RNN이해하기

이전 MLP와 유사한 모양이다.
먼저 데이터 X에 가중치행렬 W1를 곱하고 bias를 더한 뒤 활성화함수를 곱한다.
$H = \sigma(XW^{(1)}+b^{(1)})$
그 다음, 다시 가중치행렬 W2를 곱하고 bias를 더해 최종 출력을 한다.(2 layers)
$O = XW^{(2)}+b^{(2)}$

여기서 W1, W2는 시퀀스데이터와 관계없이 공유되는 가중치 행렬이다.
H는 잠재변수, $\sigma$는 활성화함수, b는 bias이다.

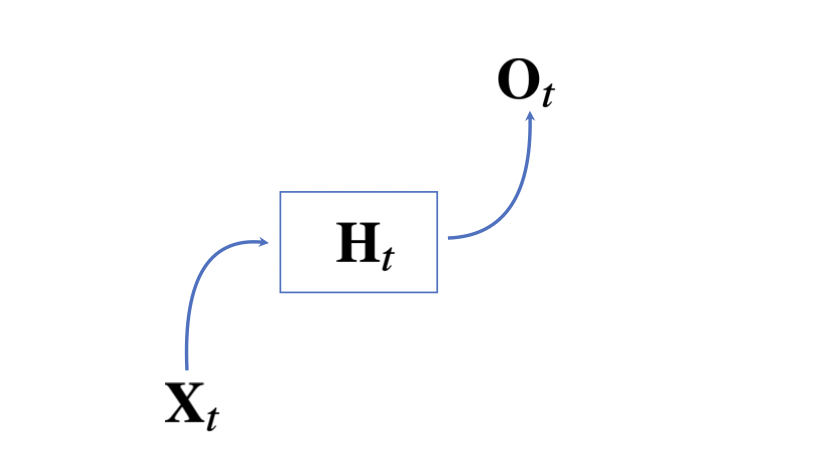
위의 형태는 과거의 정보를 다루지 않는다. 정확하게 t시점에서의 데이터에 대해서만 계산하기 때문이다.

이 문제를 해결하기위해 이전 순서의 잠재변수와 현재의 입력을 활용하여 모델링을 진행하는 방식이 RNN모형이다.

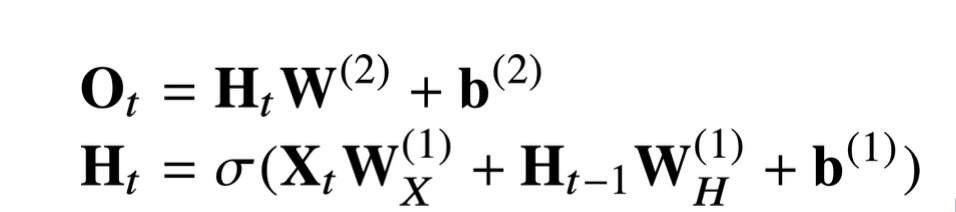
위에서 세 개의 가중치 행렬이 등장하고, 가중치 행렬은 t에 의해 변하지 않는다는 것과 t에 따라 변하는 것은 X, H라는 것을 알아두자.

위의 방법까지는 RNN의 순전파이다. 역전파는 반대의 모양으로 만들어지게 되는데, 잠재변수의 연결그래프에 따라 순차적으로 계산하게 된다.(BPTT) 따라서 잠재변수는 두가지 입력을 받게 되는데, 출력에서 오는 Gradient와 그 다음 시점에서의 Gradient이다. 또한 값을 전달받은 H는 다시 입력과 그 전 시점의 H로 값을 전달해주는 방식이다.

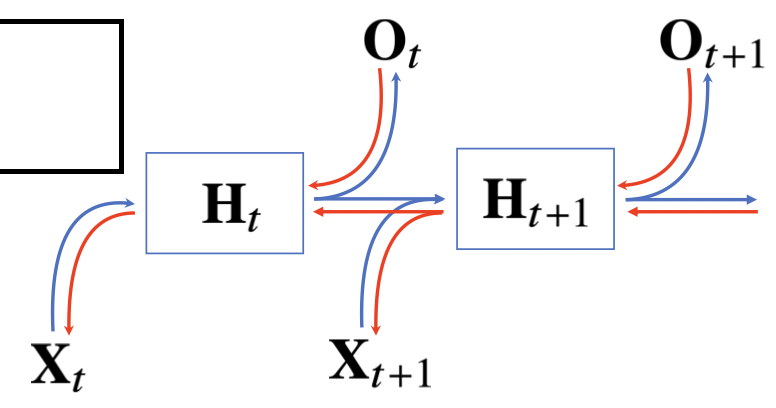
우리는 가중치 행렬의 미분을 아래와 같이 계산할 수 있다.

위 수식의 마지막 $\prod$연산의 미분값은 현재시점으로부터 멀어질 수록 그 값이 매우 커지거나 작아지게 되어 매우 불안정해진다. 보통 기울기 소실 문제라고 부르며, 이 문제를 해결하기 위해 시퀀스의 길이를 끊어주어야 한다.

이를 Truncated BPTT라고 부르는데, Gradient를 전달할 때 특정 시점에서 끊어주어서 잠재변수로부터 Gradient를 전달받지 않고 출력으로부터의 Gradient만 전달받는 방식을 사용한다.

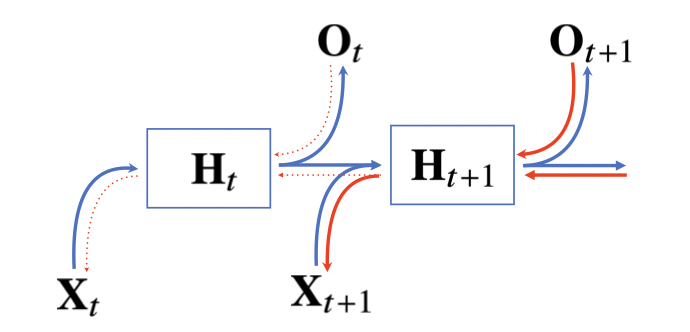
이러한 방법이 완전한 해결책이 되지는 못한다. 따라서 최근에는 긴 시퀀스를 처리하는데 있어서 기본적인 RNN을 사용하기보다 GRU, LSTM등을 사용하는 추세이다.

임성빈 교수님 마스터 클래스

kakaobrain - UNIST 인공지능대학원 교수

• Statistical Learning
• Reinforcement Learning
• Stochastic Optimization
• Causal Inference
  머신러닝 분야에서 최근 주목받는 분야
  데이터 사이언스 분야에서 중요!
  

수학공부 어려운데 쉽게 공부하는 방법?
머리로는 어렵지만 손으로 익히는 건 가능하다!!

익숙해지는 방법

Q. 익숙해지는 방법
용어의 정의는 일단 외우는 것부터 시작한다. 교과서나 위키피디아를 활용, 또는 인공지능 커뮤니티에 물어보자!(Tensorflow KR, Pytorch KR)

용어를 외웠다면 예제를 찾아보도록 하자.

Q. 여러 모델들의 수학적 원리를 모두 이해하고 있어야하나요?

• 모두 이해하는 것은 어렵지만 적어도 이해하는데 필요한 기초는 갖춰야 한다.
• 본인은 매일 아침 한 시간 동안 공부한다.

Q. 선형대수/확률론 /통계학

• 기업 및 대학원 면접 때 정말 많이 물어봄
• 알고리즘이랑 최적화 내용도 같이 공부하면 시너지가 좋다.
• 머신러닝 이론을 공부할 게 아니라면 해석학/위상수학까지 공부할 필요는 없어요
• 기초 자체를 공부하기보다 머신러닝에서 어떻게 활용되는지 검색해보자.
  예) 분류문제에서 왜 cross entropy를 손실함수로 사용하는가?
• 기초 공부는 기초에서 끝나는 게 아니라 걔네들을 어떻게 활용하는지 이해해야 완성!
  Dive into Deep Learning

Q. ML엔지니어는 수학을 어느 정도 알아야할까요?

• 필요한 걸 공부해서 빠르게 따라잡을 수 있을만큼 알아야 한다.

Q. 수학이 어디서 쓰이는가?

• 문제를 정의하고 Brainstorming(정보를 모아서 솔루션을 구하고) 하는데 필요하다.
• 기술적인 Implement나 Analyze(결과 테스트, 문서화)에는 사실 크게 필요하지 않다.

Q. 추천시스템 공부할 때 알아야 할 내용?

• Doive into Deep Learning 16장 참고!
• Multi-Armed Bandit

Q. 인공지능대학원 관심있어요!

• 카이스트, 서울대, .. 등등 있는데 학석박 간에 어떤 차이?
• 분야마다 다르겠지만 전문성이 다르고, 대중화되지 않은 영역은 학위과정이 중요!
• CV, NLP와 같은 분야는 굳이 대학원에 안가도 가능한 수준!
• 인터넷에 다양한 소스들이 많기 때문
• 강화학습, Causal Inference 등의 분야는 학위가 중요할 수 있다.

Q. Explainable,,

• 학사수준으로는 어렵다. 평가하는 방법에 대한 것 자체가 연구하기 시작한지 얼마 되지 않은 분야.

Q. 학부생이고 취업을 하고 싶은데 대학원생과 견줄 만한 스펙을 갖출 수 있는 활동을 추천해주세요

• 논문을 주고 구현한다든지, 새로운 문제를 풀어보라든지..와 같은 트레이닝되어있는 것을 선호하는 것. 대학원을 선호하는 것이 아니라 대학원 내에서 갖춘 실력을 선호하는 것. 즉, 전문성을 평가하는 것.
• 그 분야에서 논문을 썼느냐.
• 이 사람이 과연 이 분야에서 중요한 기술적인 것들을 직접 구현해서 오픈소스로 만들었는지
• Tensorflow아니고 Pytorch로 구현했다? 더 좋아해요
• Lab에서 인턴을 많이 연계해주고, 같이 일해본 사람들을 ㅃㅂ게 된다.
• 레퍼런스 검증 : 교수님 추천, 인턴 실습 회사 추천 등

Q. 딥러닝 서적

• Dive into deep learning
• 밑바닥부터 시작하는 딥러닝 123

Q. 심슨의 역설과 같은 통계의 오류같은 것들이 잘 정리된 책들이 있을까요?

• book of why
• 영어로 된 책,,,,,

Q. 어느정도 ?

• 주니어라면 line by line 으로 연습을 계속 해보는 것이 좋다. 회사 들어가기 전에 하냐 들어가고 나서 하냐 차이. 들어가기 전에 하는게 좋고, 다 하면 너무 오래걸리니까 정말 중요한 것들(논문에서 구현하는...)을 위주로,,
  딥러닝 프레임워크가 지원하는 부분은 기초적인 개념정도만 알고 있어야하지만
  line by line으로 구현해야만 하는 부분이 있다. 연습해볼만한 가치가 있을 것 같다고 생각이 든다면 해보길 권장
  역행렬을 구하던가 그런거는 비추천

나중에 시니어 엔지니어가 된다면 이론에 대해서 디테일하게 잘 알고 있어야 할 것.

논문 구현하는데 명확하지 않은 부분?

• 명확하지 않은 것은 엔지니어의 상상력이다.
• 기상천외한 상상력이 아니라 비슷한 상황에서 어떤 시도를 했는지 알아보고, 검색해봐야 한다.
• 먼저 구현하기 쉬운 논문부터 구현하는 것을 연습하자.
• 공부는 혼자하지 말자. 주변인들에게 물어보면서 하자!!!!!
• 질문에 대한 대답을 열정적으로 해주실 것이다.

멘토링
이 현 멘토님
통계학과

모수를 안다 = 분포를 안다

모집단 : 분포가 궁금한 집단, 모르는 집단