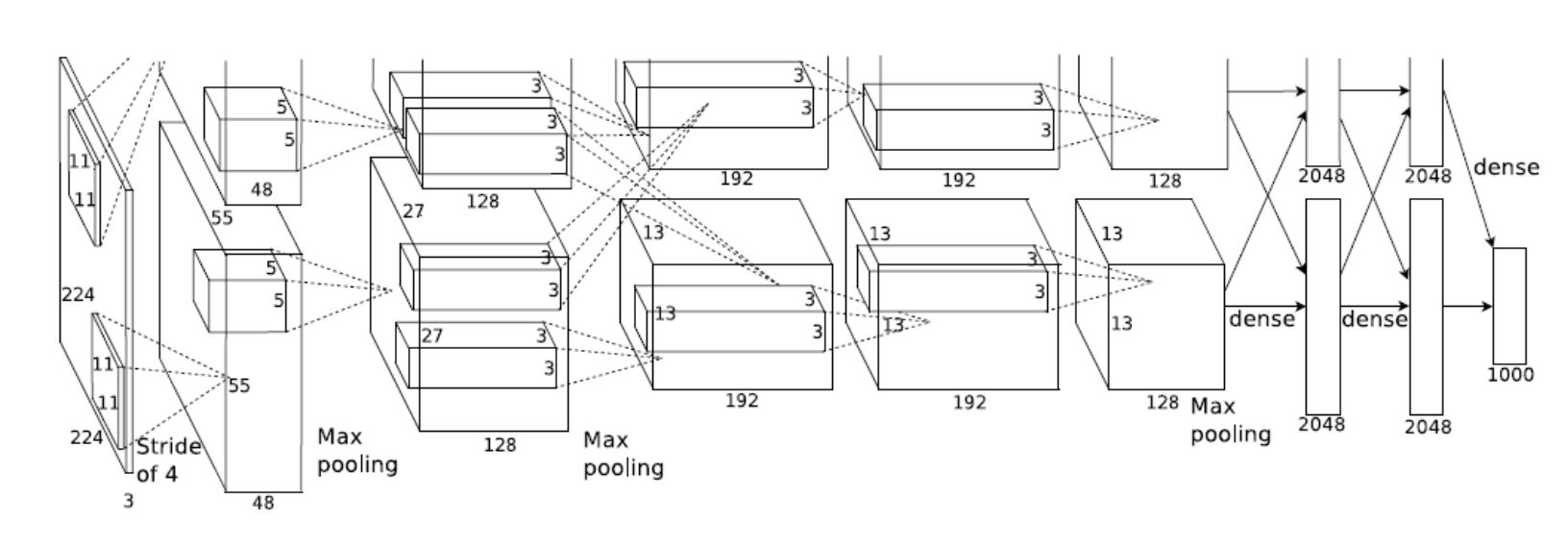
CNN
1. Convolution이란 무엇인가
Convolution의 정의
Convolution 연산 방법과 기능
(RGB는 3채널)
Input Channel과 output convolution feature map의 channel을 알면 여기에 적용되는 convolution feature의 크기 역시 알 수 있다.
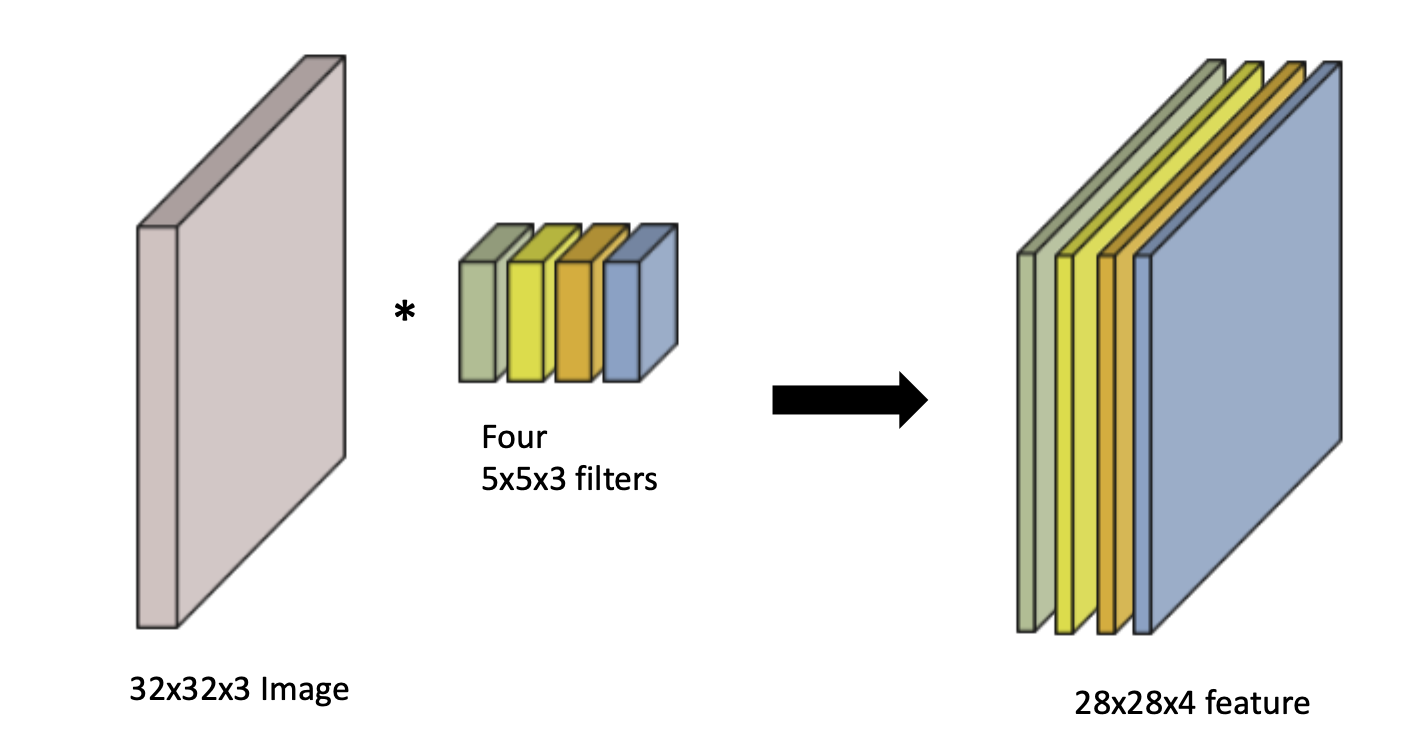
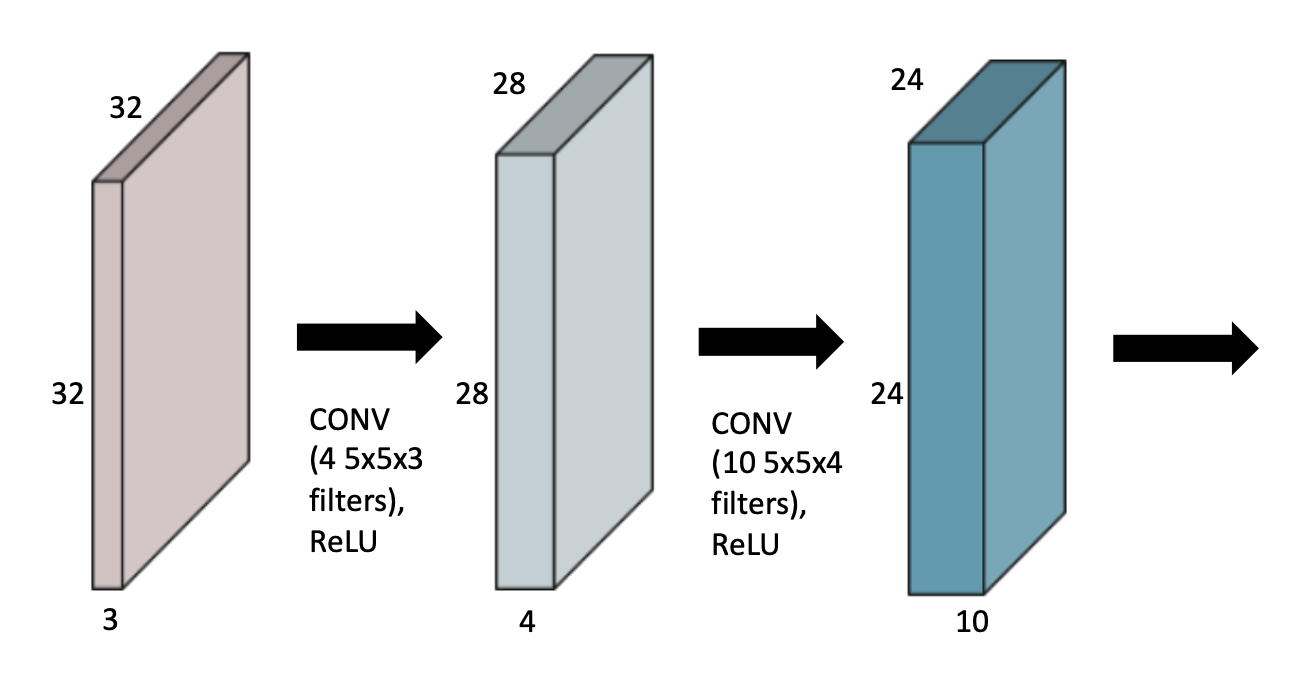
파라미터의 숫자를 잘 보자.
첫 번째 CONV에서는 4개의 5x5x3 conv filter가 필요하다.
두 번째 CONV에서는 10개의 5x5x4의 conv filter가 필요하다.
최근에서는 Fully connected layer가 점점 사라지는 추세. 기계 학습에서 parameter 수가 많을 수록 Gerneralization performance가 줄어들게 된다. 따라서 Deep하게, 파라미터를 줄이는 방식으로 학습을 하게 된다.
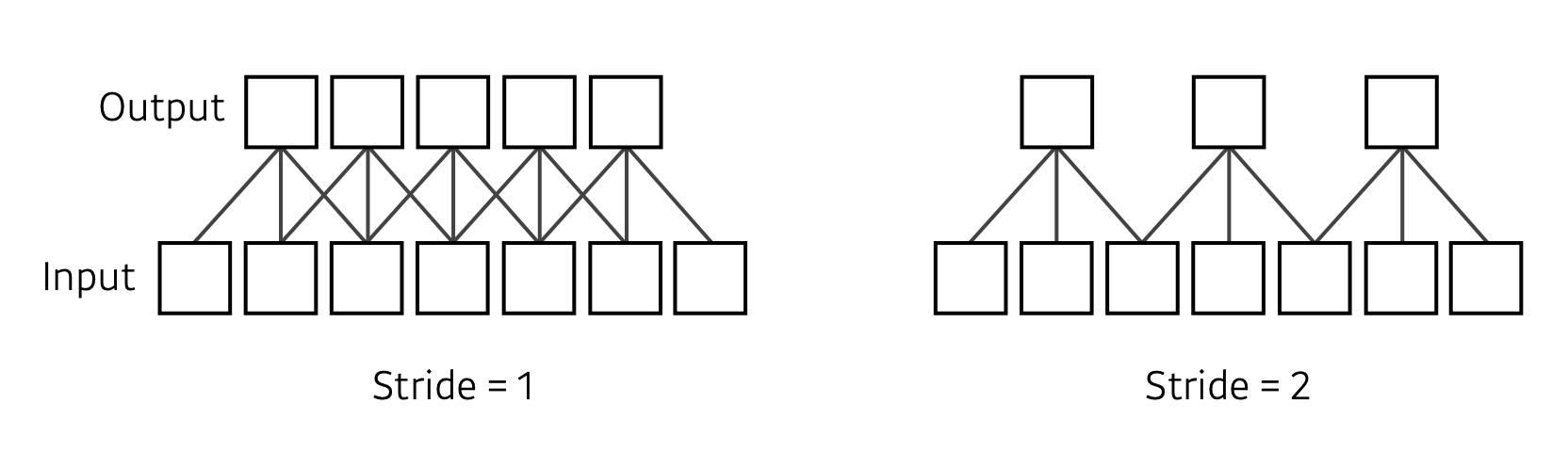
Stride
넓게 걷는다. 보폭이라고 생각하자.
Padding
가장자리 값을 채워준다.
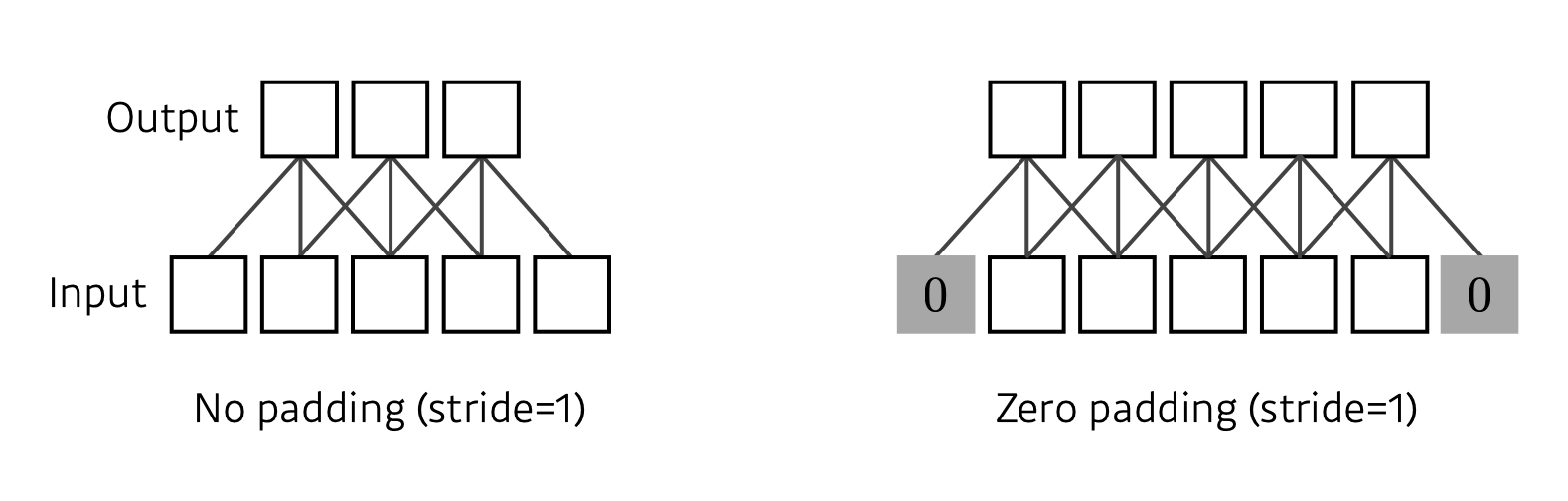
커널의 크기에 맞게 적절한 패딩값을 설정하면 CONV의 Input과 Output이 같은 형태를 지니게 된다.
파라미터 수 계산
(Kernel의 가로) X (세로) (input 채널 수) (output 채널 수)
이런 계산을 통한 사이즈에 감이 생길 수 있어야 한다.
Exercise
최근에는 Fully connected layer는 줄이고 convolution을 깊게 만들어 파라미터 수를 줄이는 시도를 한다.
Dimension Reduction, 1X1 CONV
이미지에서 영역을 보는 것은 아니다. 1 pixel로 채널 방향으로 진행하는 것.
- conv layer를 깊게 쌓고 파라미터 수를 줄일 수 있는 방법이다.
2016 Stanford Winter Quarter class Youtube 영상
2. Modern CNN - 1X1 Conv의 중요성
5개 Network 들의 주요 아이디어와 구조
ILSVRC
- ImageNet Large-Scale Visual Recognition Challenge
AlexNet

8단의 CNN Net으로, Input이 들어오고 11x11 필터를 사용하는데, 하나의 convolution 레벨에서 볼 수 있는 영역은 넓어지지만 파라미터 수가 늘어나게 된다.
특징
2012년도에 시도했다는 것에 큰 의미
- ReLU activation을 사용했다.
- 비선형- slope이 1이어서 gradient가 사라지지 않음
- 기울기 소실문제 해결
- 2개의 GPU 사용
- LRN(Local Response Normalization,response가 많이 나오는 local area에 대한 정규화)
- Overlapping pooling
- Data Augmentation
- Dropout
VGGNet
특징
- 3x3 convolution filter만 사용함(stride 1)
- 1x1 conv 사용
- Dropout(p = 0.5)
- layer 16, 19개
왜 3x3일까?
conv filter의 크기가 커지면 하나의 fiter에서 고려되는 input의 크기가 커진다는 이점이 있다. (Receptive Field)
3x3 convolution filter를 2번 거치면 Receptive filter는 5x5가 될 것이다.
GoogLeNet
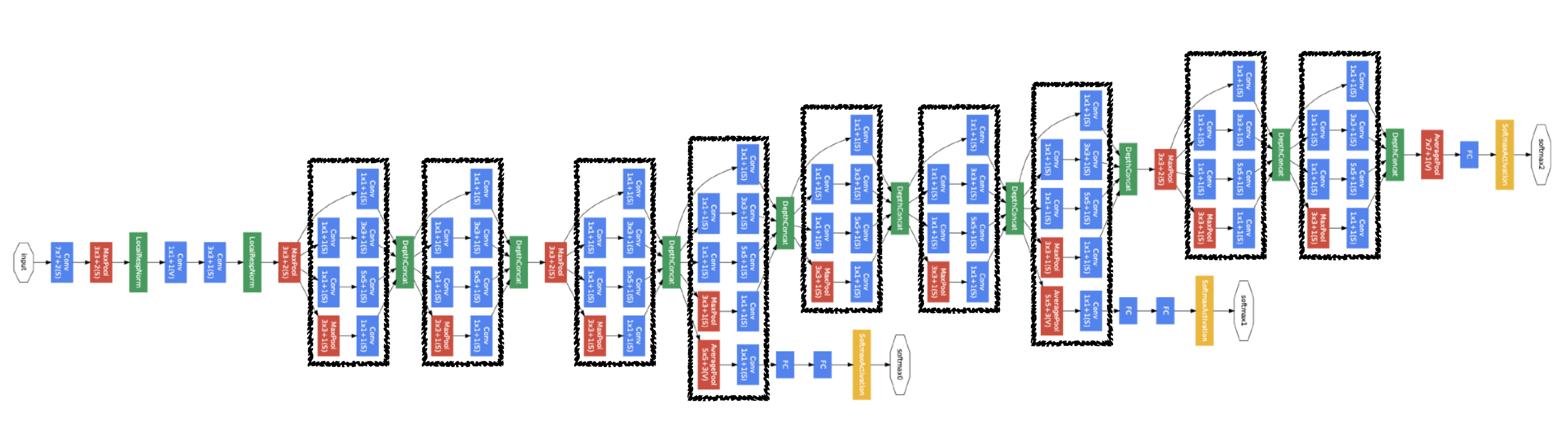
비슷하게 생긴 네트워크가 반복된다.(Network in Network)
특징
-
Inception Block
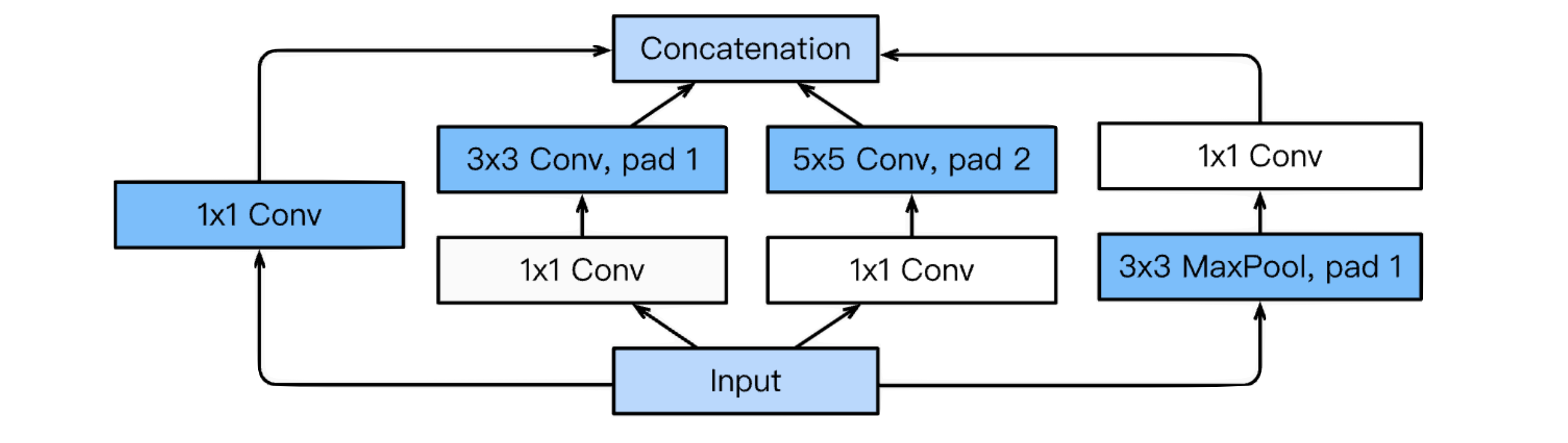
하나의 입력에 대해서 여러개의 Rceptive Filter를 거치고 여러개의 Response를 합치는 것도 중요하지만,
1x1 컨볼루션을 추가함으로써 파라미터 수를 줄였다.(채널 방향) -
Benefit of 1x1 Conv
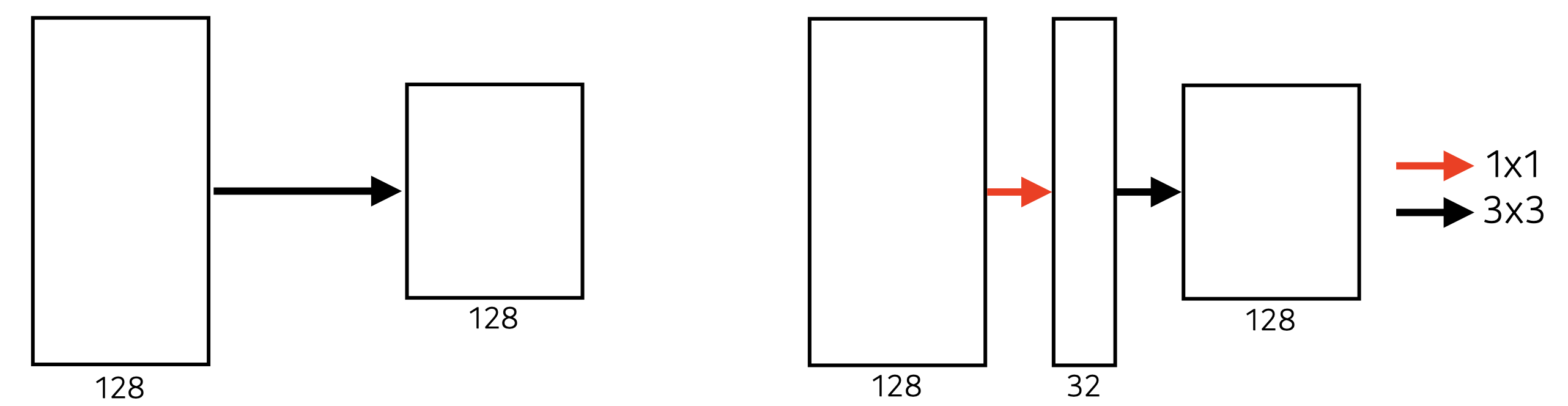
Left :
Right :
Quiz
parameter의 수가 가장 작은 CNN architecture는?
: GoogLeNet(4M), AlexNet(60M), VGGNet(110M)
ResNet
일반적으로 파라미터의 수가 많으면 Overfitting의 가능성이 생긴다. Genralization 문제가 생기는 것. 그러나 CNN에서는 overfitting의 문제는 아니다.
문제는 layer를 깊게 쌓았는데도 낮은 layer에 비해 성능이 좋지 않게 나올 수 있다는 것.
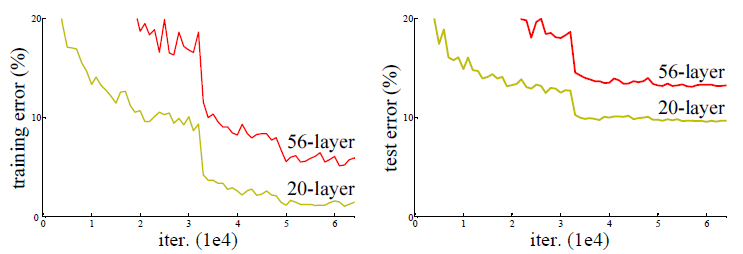
즉, Resnet저자들은 기존의 방식이 아닌 새로운 방식을 통해야 망을 깊게 만드는 효과를 볼 수 있을 것이라고 생각했다.
Residual Connection(Identity Map)

기존의 신경망은 입력값 x를 타겟값 y로 매핑하는 함수 H(x)를 얻는 것이 목적이었다. 그러나 ResNet은 위 그림과 같이 F(x) + x를 최소화하는 것을 목적으로 한다. x는 현시점에서 변할 수 없는 값이므로 F(x)를 최소로 해준다는 것은 H(x) - x를 최소로 해주는 것과 동일한 의미를 지닌다. 여기서 H(x) - x를 잔차(residual)라고 한다. 즉, 잔차를 최소로 해주는 것이므로 ResNet이란 이름이 붙게 된다.
bottleneck architecture
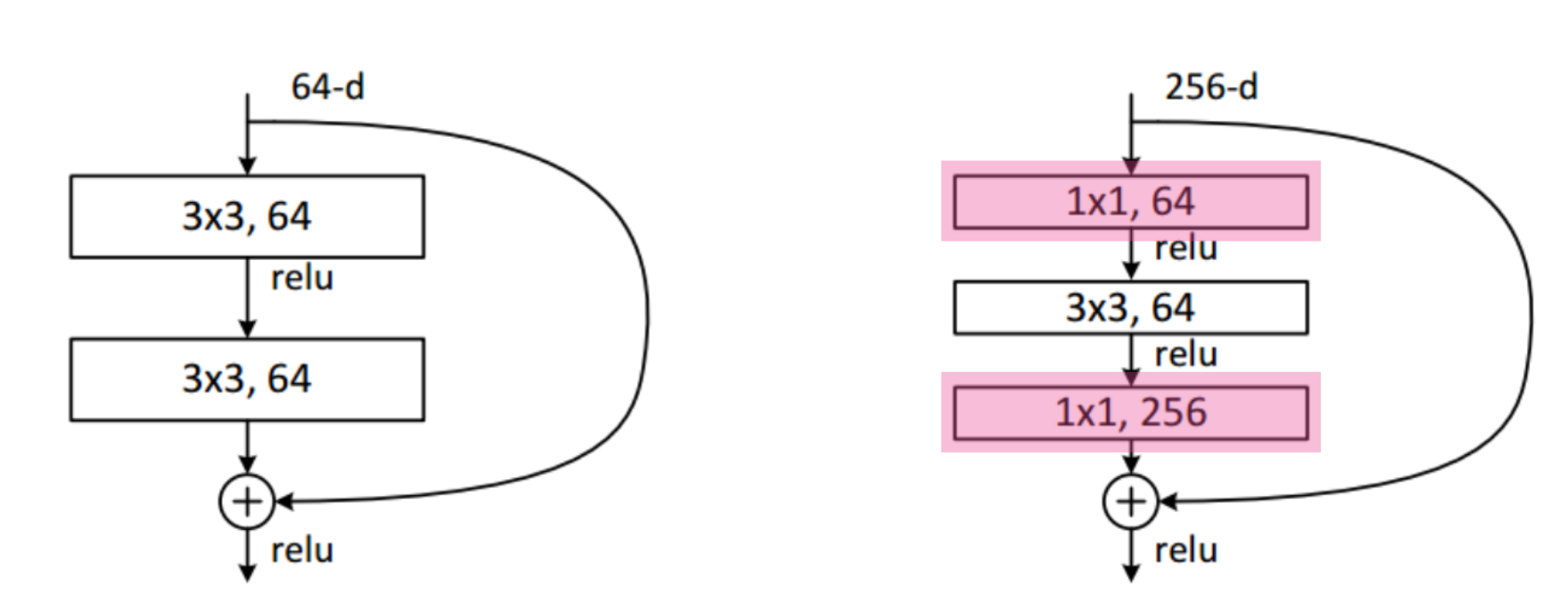
DenseNet
Concatenation instead of Addition
채널이 점점 커지고 파라미터 수가 점점 커지기 때문에 중간에 채널을 줄여주는 방식이 필요하다.
- Dense Block(늘리기)
concatenates - Transition Block(줄이기)
batchnorm -> 1x1 conv -> 2x2 avgpooling
3. Computer Vision Applications
- Computer Vision 에서 CNN을 이용한 분야
- Semantic segmentation의 정의, 핵심 아이디어
- Object detection의 정의, 핵심 아이디어, 종류
Semantic Segmentation
(Dense Classification으로도 불린다)
자율주행에서 활용되는 기술이다.
Fully Convolutional Network
Dense Layer를 없애는 방식이다. Input과 Output의 형태나 파라미터의 수는 완전히 똑같다. 그저 데이터를 쭉 폈는가 아닌가 차이이다. 이런 작업을 Convolutionalization 이라고 한다.
왜?
Fully Convolutional Network는 input의 Spatial dimension에 독립적이다. Transforming fully connected layers into convolution layers enables a classification net to output a heat map.
While FCN can run with inputs of any size, the output dimensions are typically reduced by subsampling. So we need a way to connect the coarse output to the dense pixels.
Deconvolution(conv transpose)
convolution의 역 연산이라고 생각할 수 있다(엄밀히는 아니다). stride가 2일 때 convolution을 통해 input data의 사이즈를 반으로 줄였다면 deconvolution을 통해서는 사이즈를 두 배로 늘릴 수 있다.
Detection
R-CNN

랜덤하게 이미지에서 바운더리 박스를 정한 뒤 SVM을 최종적으로 사용한다.
SPPNet
CNN을 한 번 돌려서 학습한다.
Fast R-CNN
SPP와 동일한 컨셉이다. Bounding Box Regressor를 통해 박스 이동을 예측한다.
Faster R-CNN
Region Proposal Network + Fast R - CNN
- RPN
- 특정 영역이 바운딩 박스로서의 의미가 있을지 없을지(Region Proposal)을 확인
- k Anchor Boxes(미리 정해놓은 바운딩 박스의 크기들)
- Fully Convolution Network 사용- 9 diffrent (region size, ratios)
- 4 bounding box regression parameters
- 2 box classification
- 9*(4+2) 개
YOLO
yolo(v1)
It simultaneously predicts multiple bounding boxes and class probabilities.
No explicit bounding box sampling (compared with Faster R-CNN) -> 빠르다.
bounding box와 클래스를 찾아내는 것을 동시에 하기 때문.