[99클럽 코테 스터디 18일차 TIL] 깊이탐색

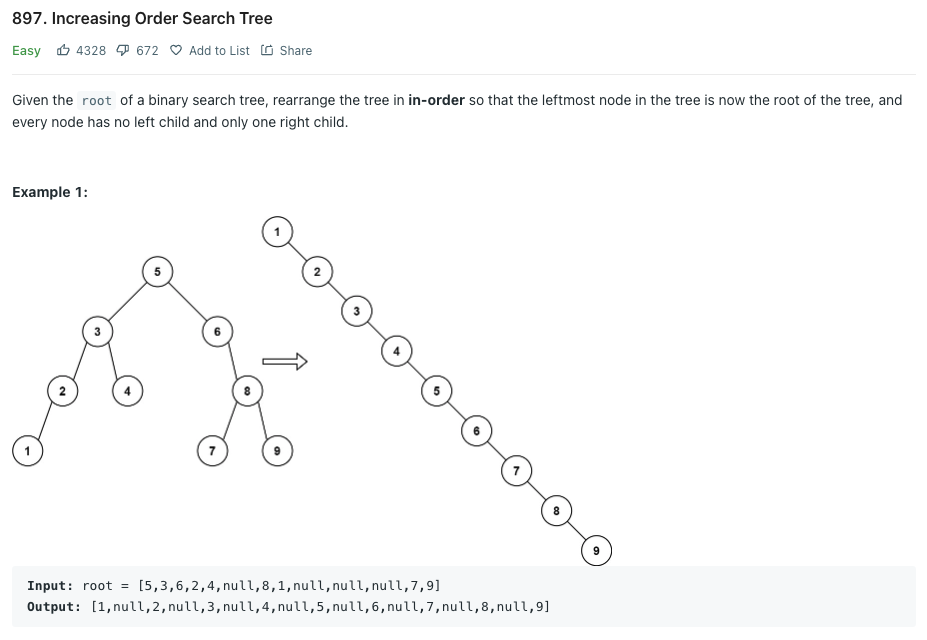
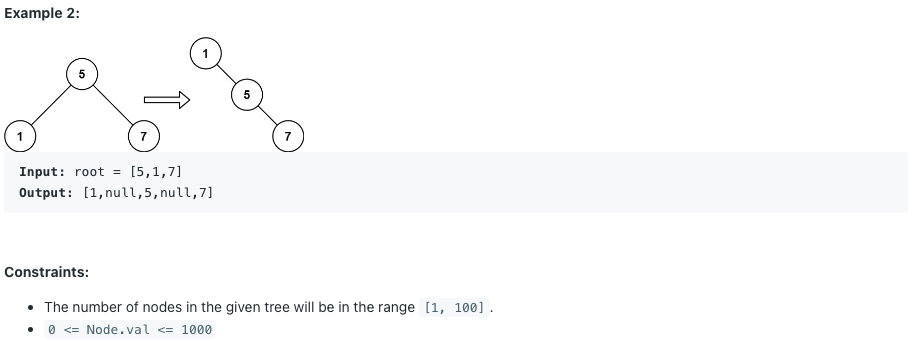
문제

답

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}


class Solution {
    private TreeNode newRoot = null;
    private TreeNode current = null;
    
    public TreeNode increasingBST(TreeNode root) {
        inOrderTraversal(root);
        return newRoot;
    }
    
    private void inOrderTraversal(TreeNode node) {
        if(node == null) return;
        
        inOrderTraversal(node.left);
        
        if(newRoot == null) {
            newRoot = new TreeNode(node.val);
            current = newRoot;
        } else {
            current.right = new TreeNode(node.val);
            current = current.right;
        }
        
        inOrderTraversal(node.right);
    }
}

문제해결

• 이진 탐색 트리(Binary Search Tree, BST)
  왼쪽 서브트리의 모든 노드들은 현재 노드보다 작다.
  오른쪽 서브트리의 모든 노드들은 현재 노드보다 크다.

• 중위 순회(in-order)
  트리를 순회하는 방법 중 하나로, 트리의 노드들을 왼쪽에서 오른쪽으로 순서대로 방문하는 방식이다.
  이 순회 방법을 사용하면 이진 탐색 트리에서는 노드들이 오름차순으로 방문하게 된다.

- 이진 탐색 트리 구조
    5
   / \
  3   7
 / \   \
2   4   8

- 중위 순회
2 -> 3 -> 4 -> 5 -> 7 -> 8

문제를 해결하기 위해
1. 이진 탐색 트리를 중위 순회한 후,
2. 모든 노드를 오름차순으로 나열하는 새로운 트리를 만들어야 한다.
(새로운 트리에서는 각 노드가 오직 오른쪽 자식만을 가지며, 왼쪽 자식은 없다.)

• 새로운 트리 만들기
  새로운 트리를 만들기 위해서 어떻게 접근해야 할지 아예 감이 안 잡혀서, gpt한테 힌트를 얻었다.
  우선 class 내부에 변수 newRoot를 선언하여 새로운 트리를 선언한다.

• 오른쪽 트리만 있는 구조 만들기
  그렇다면 오름차순으로 나열한 오른쪽 트리만 있는 구조는 어떻게 만들어야 할지 또 난관에 봉착했다.

1. current 내부변수 추가
   이를 위해 class 내부 변수로 current 를 선언해서, 새로운 노드를 current.right 에만 추가하고, 이를 current로 변경해준다.

2. inOrderTraversal 메서드 내부에 재귀함수 호출
   트리 구조에서는 재귀함수를 빼 놓을 수 없는데, 재귀함수를 언제 호출하며, 인자값을 무엇으로 주어주느냐 고민했다. 먼저 오름차순으로 정렬해야 하기 때문에 node.left를 먼저 인자로 넣어주고, 그 후 newRoot/current 를 처리하는 로직을 배치한 후, 마지막에 node.right 를 인자로 넣어서 재귀함수를 또 한번 호출해준다.

3. newRoot/current 내부변수 조작
   newRoot 는 최상단 노드로 오름차순 정렬시 첫번째 값이 들어간다.
   일단 newRoot의 null 여부로 분기를 가르고, null 인경우 new TreeNode로 값을 생성하고, current 를 newRoot로 할당한다.
   만약 newRoot가 null이 아닐 경우, 새로운 트리는 오른쪽 트리만 가지기 때문에, current.right 에 new TreeNode를 추가하고, current 는 current.right 으로 재할당해준다.

회고

트리 구조 문제 좀 풀었다고, 이제 풀수 있을거란 오만한 생각을 함.
계속 새로운 문제를 접하면서 언젠가 능숙하게 풀 수 있는 날이 오기를..
오늘 문제는 gpt 문제풀이를 보고도 이해하는데 한참 걸렸다. 복습 여러번 해야 할듯
아좌좌~