
손실 함수
실제 값과 예측 값의 오차를 의미한다.
손실 함수가 작을수록 예측이 정확함을 의미한다.
오차 함수(Error Function), 비용 함수(Cost Function), 목표 함수(Objective Function) 이라고도 한다.
최적화 (Optimizer)
딥러닝은 데이터들 사이에서 숨겨진 규칙을 찾아낼 때 사용한다.
즉 적절한 가중치를 처음부터 알 수는 없다는 것이다.
그렇다면 어떻게 적절한 가중치를 찾아낼 수 있을까?
1) 먼저 각 층에 임의의 가중치를 설정한다. (보통 가중치는 0, 편향은 1로 설정한다.)
2) 출력값을 계산한 후, 오차가 허용 오차 이내가 되도록 각 층의 가중치를 업데이트한다.
이 과정에서 출력값과 실제값의 차이를 나타내는 지표로 사용되는 것이 손실함수다.
손실함수를 최소화시키기 위해, 가중치의 미분을 계산하고 그 값을 기반으로 가중치를 갱신해간다.
이 기울기를 기반으로 최적의 미분 값을 찾아가는 방식을 최적화라고 하며, 이에 사용되는 것이 역전파와 경사하강법이다.
손실 함수의 종류
제곱 오차 (Square Error, SE)
- 손실을 제곱한다.
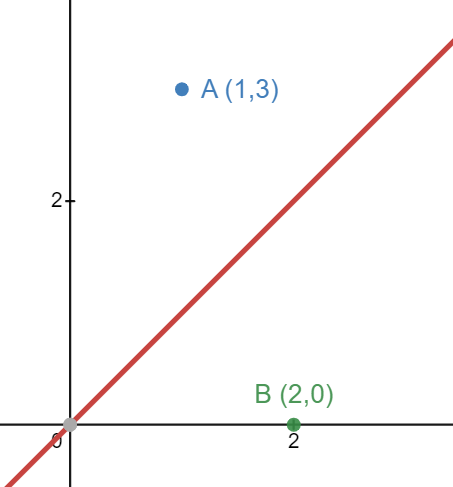
위와 같이 y=x인 실제 값에서 A는 +2, B는 -2만큼의 손실이 발생했다.
손실에서는 오차의 크기가 중요하지, 부호는 의미가 없다.
그런데 부호 때문에 둘의 손실이 다르다고 느껴질 수 있기 때문에, 손실을 제곱하여 부호를 없앤다.
절대값 함수가 아니라 제곱 함수를 사용하는 이유는 무엇일까?
절대값 오차는 미분 연속적이지 않으며, 제곱 오차에 비해 오차의 크기를 작게 보여주기 때문이다.
(오차를 크게 보여주는 제곱 오차에서 학습이 더 잘된다.)
오차 제곱합 (Sum of Squares for Error, SSE)
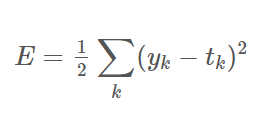
- 모든 오차의 제곱을 합한다.
가장 많이 사용되는 손실 함수다.
💡 손실함수에 사용되는 오차제곱합은 일반적인 오차제곱합에 1/2를 곱한 것이다.
교차 엔트로피 오차 (Cross Entropy Error, CEE)
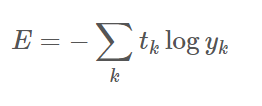
교차 엔트로피는 다중 분류 신경망에서 사용된다.
y는 신경망의 출력, t는 원-핫 인코딩 된 정답 레이블이다.
💡 원-핫-인코딩(One-Hot Encoding)
전체 벡터에 단 한 개의1이 있고, 나머지 인덱스는 전부0으로 구성된 벡터
t는 정답인 레이블은 1, 아닌 레이블은 0이다.
따라서 교차 엔트로피 수식에서
정답이 아닌 k에 대해 t * log y = 0 이므로
정답 레이블의 출력값만 고려해 계산하면 된다.
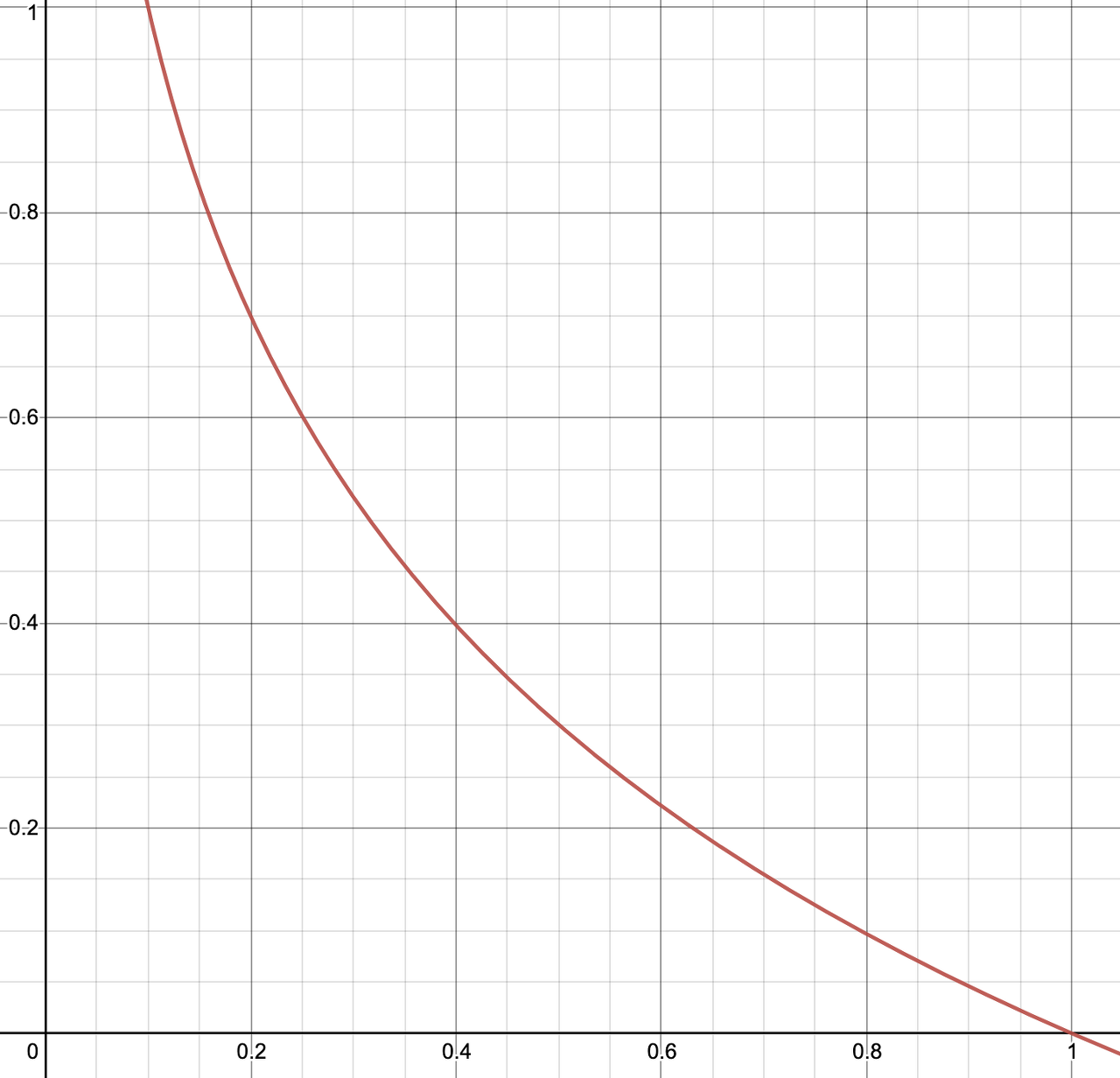
위는 y = -log(x)의 그래프다.
x(출력값)이 클수록 오차가 작아짐을 확인할 수 있다.
📑 참조
https://gooopy.tistory.com/59
https://kingnamji.tistory.com/18
