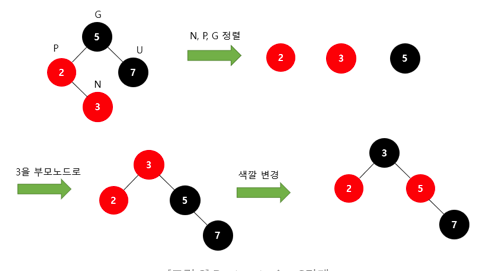
힙에 대해 설명해 주세요.
완전 이진 트리의 일종으로 반정렬 상태를 유지하여 최대 혹은 최소의 값을 빠르게 반환할 수 있는 자료구조이다. 주로 우선순위 큐를 구현하기 위해 이용된다.
힙을 배열로 구현한다고 가정하면, 어떻게 값을 저장할 수 있을까요?
루트 노드를 첫번째 인덱스에 저장하고 부모 노드의 인덱스를 기준으로 2i에 왼쪽 자식 2i+1에 오른쪽 자식을 저장한다.
힙의 삽입, 삭제 방식에 대해 설명하고, 왜 이진탐색트리와 달리 편향이 발생하지 않는지 설명해 주세요.
삽입
삽입은 맨 마지막 자리에 요소를 삽입 후 힙의 속성에 맞을 때 까지 부모와 자식간의 교환을 한다.
삭제
루트노드와 맨 마지막 요소를 스왑한 후 마지막 요소를 반환한다. 그 후 힙의 속성에 맞을 때까지 부모와 자식간의 교환을 한다.
편향이 발생하지 않는 이유
이진탐색트리에서 편향이 발생하려면 완전 정렬된 상태로 삽입이 이루어졌을 시에 발생한다. 하지만 이때 힙은 최대 혹은 최소 요소를 루트 노드로 하는 완전 이진 트리를 유지하도록 삽입 및 삭제를 하기 때문에 편향이 발생하지 않는다.
힙 정렬의 시간복잡도는 어떻게 되나요? Stable 한가요?
힙 정렬의 시간복잡도는 힙을 구성하고 나서 삭제연산을 반복하면 되므로 O(nlogN)이다. 그리고 unstable하다.
BBST (Balanced Binary Search Tree) 와, 그 종류에 대해 설명해 주세요.
이진탐색트리의 단점을 보완한 트리로 편향트리가 발생하지 않도록 삽입 혹은 삭제할때 높이의 균형을 유지하는 트리이다. 그 종류로는 AVL, red-black tree, B트리, B+ 트리 등이 있다.
Red Black Tree는 어떻게 균형을 유지할 수 있을까요?
조건
- 모든 노드는 빨간색 혹은 검은색이다.
- 루트 노드는 검은색이다.
- 모든 리프(null lif)는 검은색이다.
- 빨간색 노드의 자식은 검은색이다.
- 모든 리프노드에서 black depth 는 같다.
리프노드에서 루트노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.
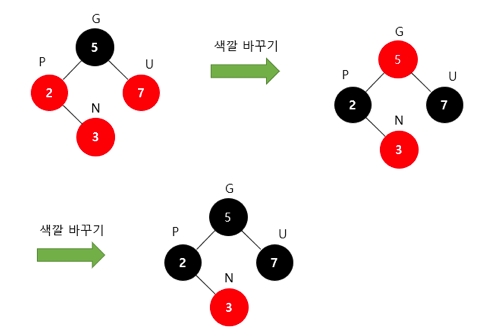
삽입 연산
- 새로운 노드는 항상 빨간색이다.
- Doulbe Red 발생할 시 삼촌 노드의 색이 검은색이면 Restructuring, 빨간색이면 Recoloring을 수행한다.
Restructuring
1. 새로운 노드 부모 노드 조상노드를 오름차순으로 정렬
2. 셋 중 중간값을 부모로 만들고 나머지 둘을 자식으로 만듬
3. 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 변경
Recoloring
1. 새로운 노드의 부모와 삼촌을 검은색으로 바꾸고 조상을 빨간색으로 바꿈.
1-1. 조상이 루트노드라면 검은색으로 바꿈
1-2. 조상을 빨간색으로 바꿨을 때 다시 문제가 발생하면 문제가 발생하지 않을 때까지 반복
삭제
- target이 red일 경우 그대로 삭제
- target이 black 경우 target 노드 쪽에 black 추가
- target의 조카들이 모두 black인 경우 부모의 색을 target과 target의 형제에게 나누어 준다.
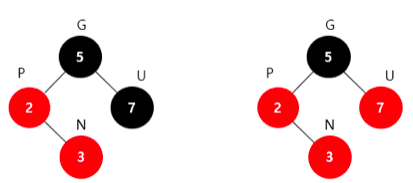
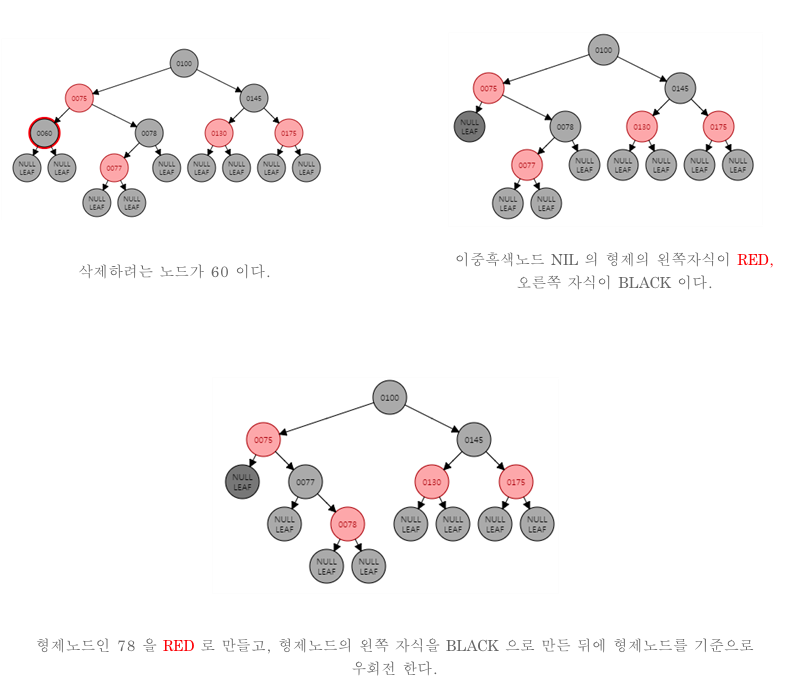
- target의 조카 중 일부가 red일 경우 회전을 이용한다.아래의 예는 이중 흑색 노드가 왼쪽에서 발생할 시 이다. 따라서 오른쪽에서 발생할 시도 고려를 해야한다.
Default
- Default는 삭제가 일어나면 무조건 실행된다.
- 삭제된 노드가 검은색인 경우, 그 자리를 대체하는 노드를 검은색으로 칠한다.
- 원래 검은색 노드를 검은색으로 칠하는 경우 이중흑색 노드가 발생한다.
case change
- 이중 흑색 노드의 형제가 빨간색인 경우 형제를 검은색 부모를 빨간색으로 칠한다. 그 후 부모를 기준으로 좌회전한다.
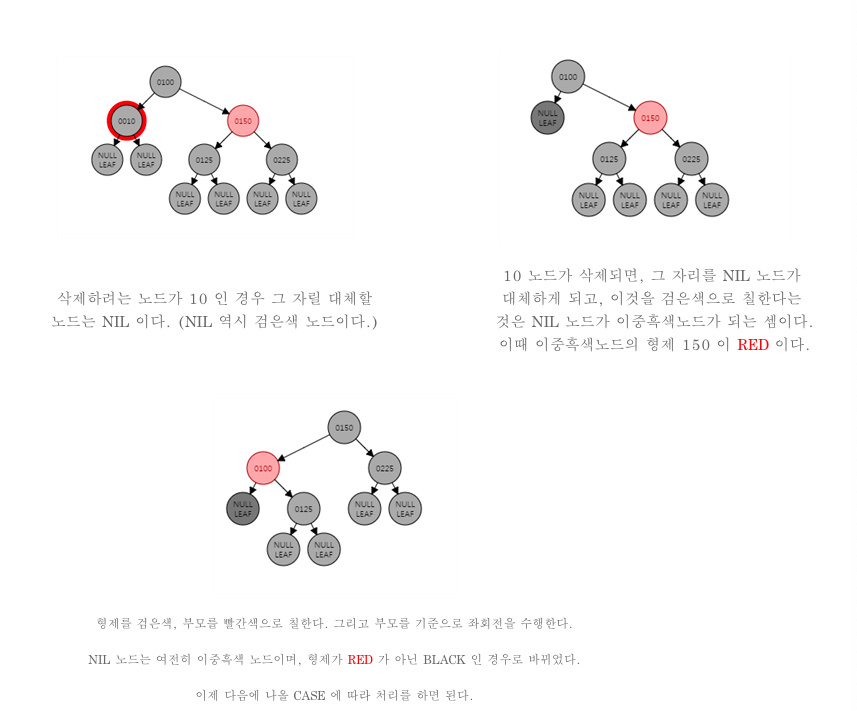
case a
- 이중 흑색 노드의 형제가 검은색인 경우 형제의 양쪽 자식 모두 검은색인 경우 형제노드만 빨간색으로 변경하고 이중 흑색 노드의 검은색 1개를 부모에게 전달한다.
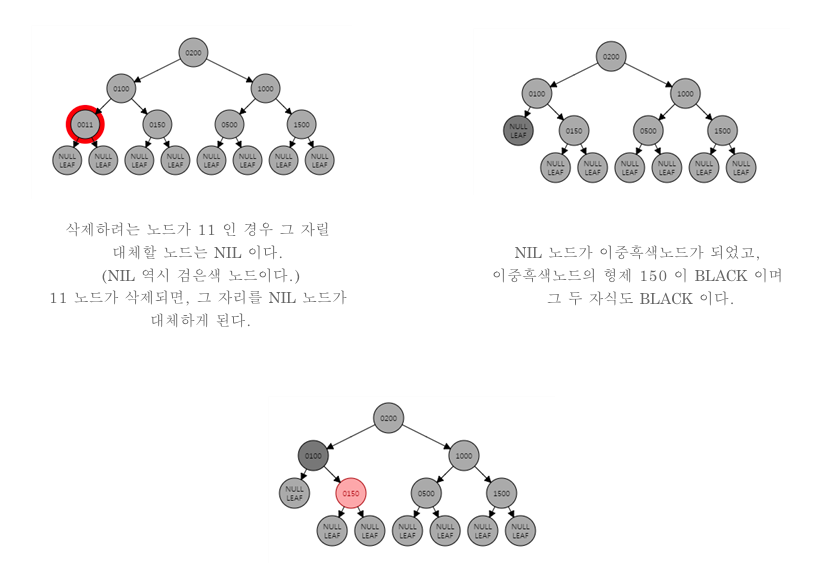
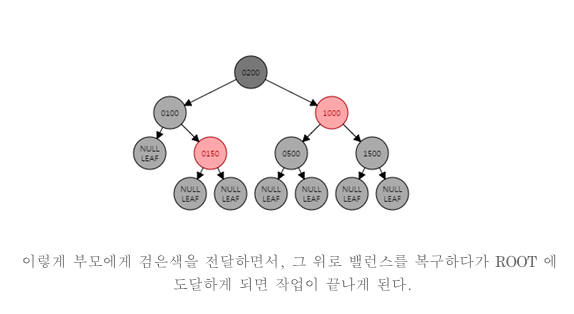
case b
- 이중 흑색 노드의 형제가 검은색이고 형제의 왼쪽 자식이 빨간색, 오른쪽 자식이 검은색인 경우 형제 노드를 빨간색으로 형제 노드의 왼쪽 자식을 검은색으로 칠한 후에 형제노드를 기준으로 우회전한다.
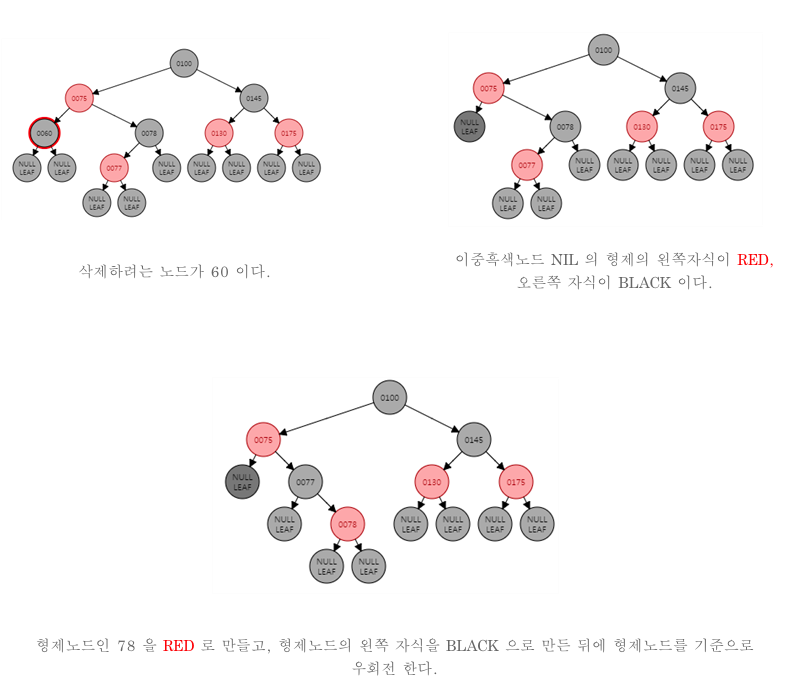
case c
- 이중 흑색 노드의 형제가 검을색이고 형제의 오른쪽 자식이 빨간색인 경우 부모 노드의 색을 형제에게 넘긴다. 부모 노드와 형제 노드의 오른쪽 자식을 검은색으로 칠한다. 부모 노드 기준으로 좌회전한다.
Red Black Tree의 주요 성질 4가지에 대해 설명해 주세요.
- 루트 노드는 검은색이다.
- 모든 리프(null lif)는 검은색이다.
- 빨간색 노드의 자식은 검은색이다.
- 모든 리프노드에서 black depth 는 같다.
2-3-4 Tree, AVL Tree 등의 다른 BBST 가 있음에도, 왜 Red Black Tree가 많이 사용될까요?
1) Red Black Tree
- 삽입, 삭제 작업 시 균형을 맞추기 위한 작업 횟수가 적다.
- 각 노드당 색깔을 표현하는 데 단 1bit의 저장공간만 필요하다.
- 언제 회전에 의해 균형을 잡아햐 하는지가 쉽게 판별된다.
- 이진 탐색 트리의 함수를 거의 그대로 사용한다.
2) AVL
- 조회 시 더 빠른 성능을 자랑한다.
- 노드에 색깔이 없다.
- 빠르지만 재균형 잡는 시간이 든다.
- 프로그래밍과 디버깅이 어렵다.
- Balance Factor를 이용해 밸런스를 유지한다. 모든 노드의 BF가 -1, 0, 1 중 하나여야 한다.
BF(K) = K의 왼쪽 서브트리의 높이 - 오른쪽 서브 트리의 높이
LL(Left Left) case
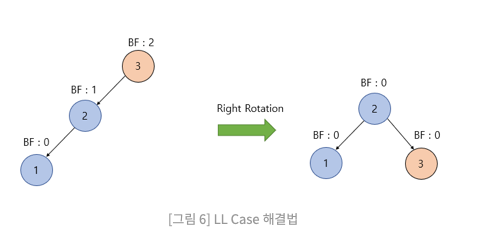
위 그림처럼 BF가 벗어난 노드를 기준으로 우회전을 적용한다.
RR(Right Right) case
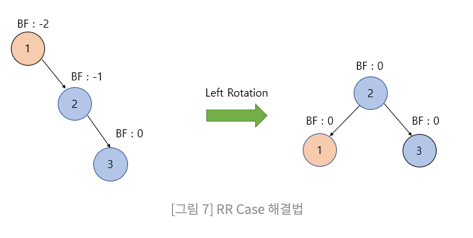
위 그림처럼 BF가 벗어난 노드를 기준으로 좌회전을 적용한다.
LR(Left Right) case
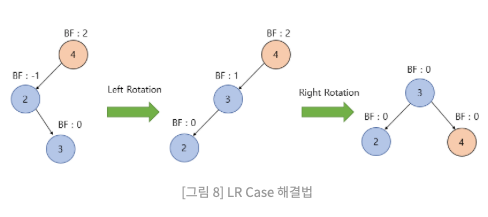
위 같은 케이스일 시 BF에 이상이 있는 노드의 왼쪽 자식 노드를 기준으로 좌회전한다. 그 후 BF에 이상이 있는 노드를 기준으로 우회전을 진행한다.
RL(Right Left) case
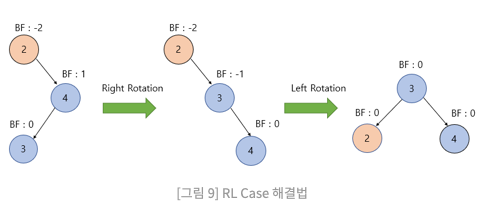
위 같은 케이스일 시 BF에 이상이 있는 노드의 오른쪽 자식 기준으로 우회전한 후, BF에 이상이 있는 노드를 기준으로 좌회전한다.
3) 2-3-4 트리
- 2 노드, 3 노드, 4 노드가 있는 균형 탐색 트리
- n 노드란 n-1개의 키와 n개의 자식 가지고 있다는 의미이다. - 한 노드의 한 키의 왼쪽 부분 트리에 있는 모든 키 값은 그 키 값보다 작고 오른쪽 부분 트리에 있는 모든 키 값은 그 키 값보다 커야 한다.
- 모든 리프노드의 높이는 동일
- 삽입 연산은 4 노드에서 스플릿 연산이 이뤄진다.
- 노드 구조가 복잡하다.
- 삽입 삭제 코드가 복잡하다.
삭제 연산
- 삭제 연산은 리프노드에서 일어난다.
- 만약 internal node라면? 리프노드의 데이터중 삭제하려는 데이터와 가장 가까운 노드를 찾아 서로 교환한다.
- 삭제 연산은 만나는 2 노드에 대해서 두 연산 중 하나를 실행한다.
- 형제 노드가 2 노드라면 merge, 3,4 노드라면 redistribute를 수행한다.
- 루트의 경우는 두개의 자식노드의 데이터가 한개일 경우 merge
- 리프노드가 2 노드가 아니라면 그냥 삭제한다
- 2 노드라면 아래 상황에 따른다.
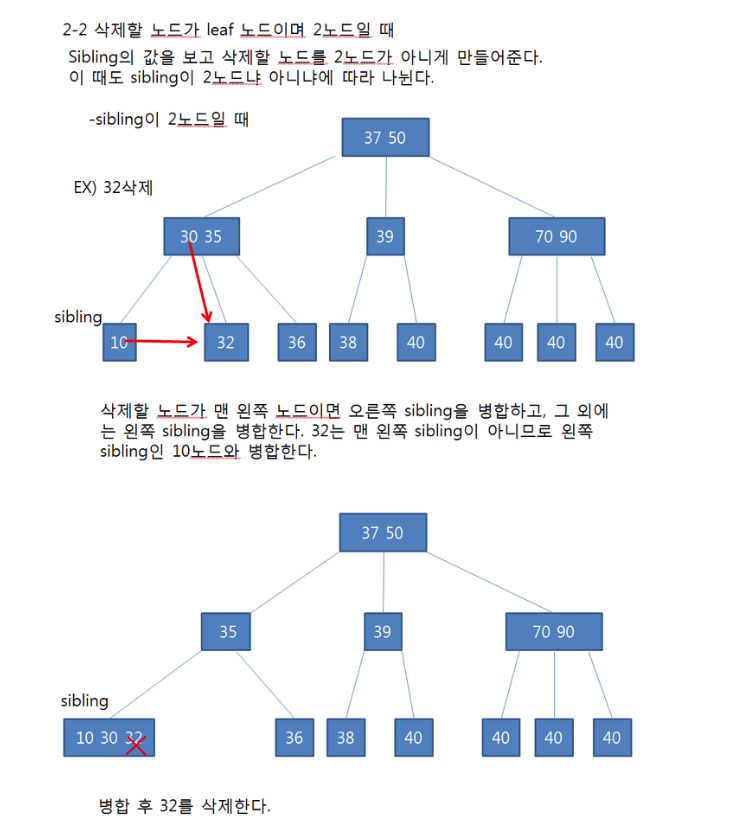
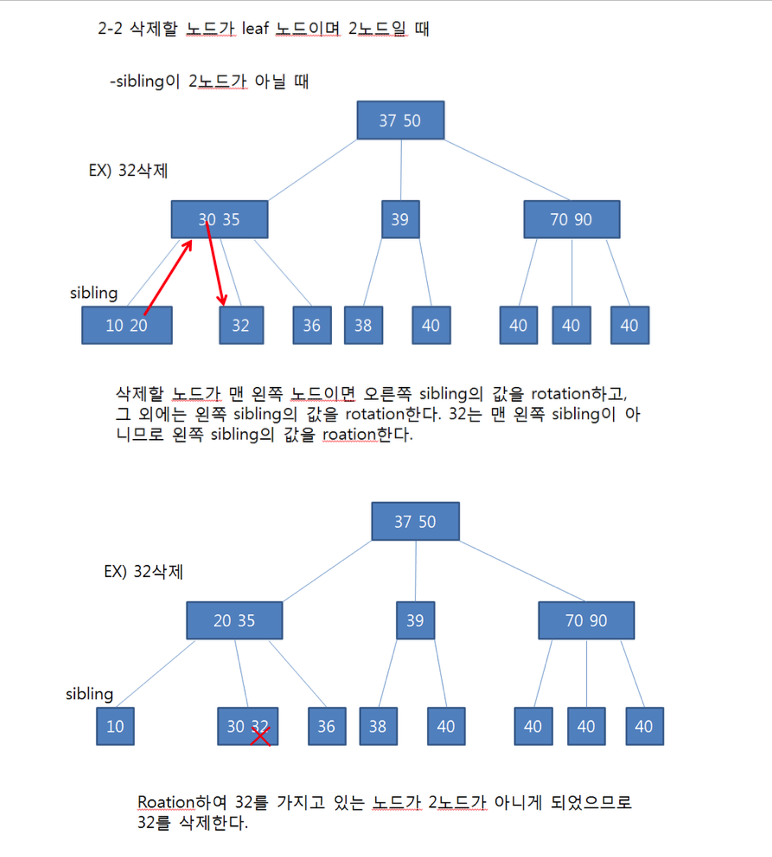
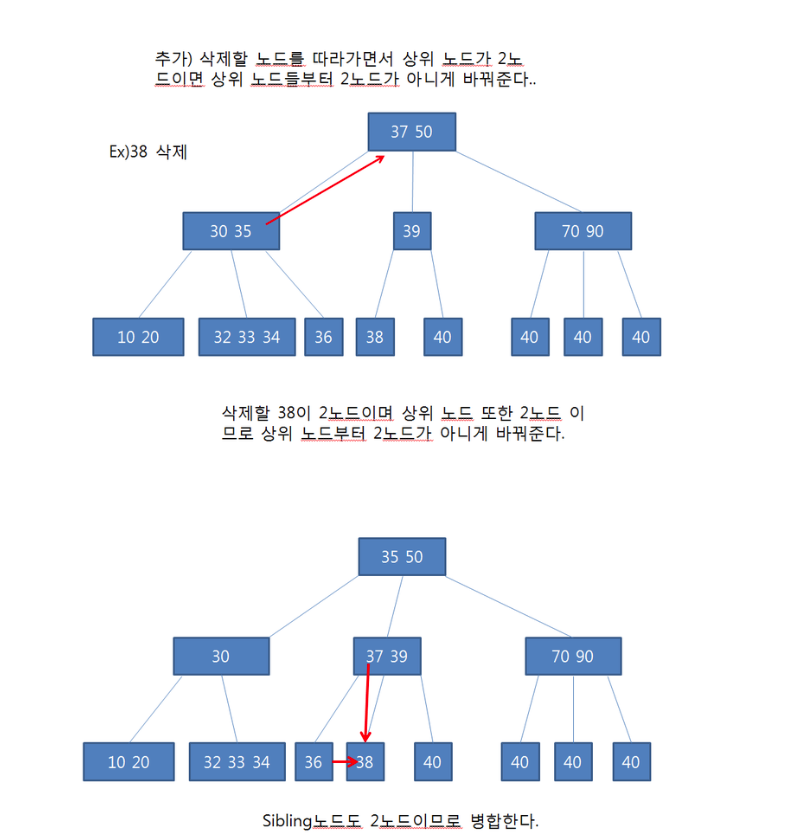
정렬 알고리즘에 대해 설명해 주세요.
정렬 알고리즘은 말 그대로 어떠한 자료구조를 정렬하는 방법으로 대표적으로 quick sort, merge sort, radix sort, counting sort, bubble sort, insertion sort, selection sort 등이 있다.
Quick Sort와 Merge Sort를 비교해 주세요.
quick sort는 pivot을 기준으로 나눠 정렬하는 기법이고, merge sort는 자료구조를 분할 후에 합치면서 정렬하는 방법이다. merge sort는 최악, 평균, 최선일 경우 모두 O(nlogn)의 소요되는 반면에 quick sort는 역순으로 정렬되어 있을 시 pivot의 효과를 볼 수 없어 최악의 경우 O(n^2)의 시간이 소요된다.
Quick Sort에서 O(N^2)이 걸리는 예시를 들고, 이를 개선할 수 있는 방법에 대해 설명해 주세요.
오름차순 혹은 내림차순으로 정렬되어 파티션이 나뉘지 않는 경우이다. 이를 개선하기 위해서는 중간값과 맨 앞값을 서로 스왑해주면 어느정도 개선이 가능하다.
Stable Sort가 무엇이고, 어떤 정렬 알고리즘이 Stable 한지 설명해 주세요.
stable sort란 중복된 값이 있을 시 이 순서가 변경되지 않는 정렬을 의미한다. insertion sort, merge sort, bubble sort, counting sort가 있다.
Merge Sort를 재귀를 사용하지 않고 구현할 수 있을까요?
큐를 이용하여 구현할 수 있다.
struct Queue<T>{...}
func merge(_ lhs: [Int], _ rhs: [Int]) -> [Int]{...}
func mergeSortWithOutRecursion(arr: [Int]) -> [Int]{
var queue = Queue<[Int]>()
for i in arr{
queue.push([i])
}
while queue.queue.count > 1{
guard let arr1 = queue.pop() else{
return
}
guard let arr2 = queue.pop() else{
return
}
queue.push(merge(arr1, arr2))
}
return queue.pop()!
}Radix Sort에 대해 설명해 주세요.
Radix sort는 자릿수를 이용해 정렬을 하는 정렬 기법이다. 0~9에 해당하는 버킷을 만들고, 낮은 자릿수 부터 진행하며, 순서대로 해당하는 자릿수의 버킷에 요소를 저장하고 정렬시키는 과정을 반복하여 정렬을 하는 기법입니다. 시간복잡도는 O(dn)으로 여기서 d는 자릿수를 의미합니다.
Bubble, Selection, Insertion Sort의 속도를 비교해 주세요.
시간복잡도는 모두 O(n^2)
값이 거의 정렬되어 있거나, 아예 정렬되어 있다면, 위 세 알고리즘의 성능 비교 결과는 달라질까요?
Selection sort는 정렬되어있을 시 비교연산만 하기 때문 O(n)의 시간복잡도를 가진다.
본인이 사용하고 있는 언어에선, 어떤 정렬 알고리즘을 사용하여 정렬 함수를 제공하고 있을까요?
timsort 사용, 다양한 종류의 실제 데이터에서 잘 수행되도록 설계된 merge sort 및 insertion sort에서 파생된 안정적인 하이브리드 정렬방법. 최선의 경우 O(n) 최악의 경우 O(nlogn)
정렬해야 하는 데이터는 50G 인데, 메모리가 4G라면, 어떤 방식으로 정렬을 진행할 수 있을까요?
- 4G 만큼 데이터를 메모리에 읽어 일반적인 정렬 알고리즘을 이용해 정렬한다.
- 그러면 13개의 파일이 생긴다.
- 280MB씩 각 파일의 앞부분을 읽어온다. (남은 280MB은 출력을 위한 버퍼)
- 280MB씩 merge를 수행하고 출력버퍼에 작성한다. 출력버퍼가 차면 파일에 쓰고 출력 버퍼를 비운다. 입력버퍼가 비워지면 다음 용량만큼 읽는다.
그래프 자료구조에 대해 설명하고, 이를 구현할 수 있는 두 방법에 대해 설명해 주세요.
그래프란 노드와 edge로 구성되어있는 자료구조이다. 이를 구현하기 위해서는 연결 리스트와 배열을 이용하여 구현할 수 있다.
각 방법에 대해, "두 정점이 연결되었는지" 확인하는 시간복잡도와 "한 정점에 연결된 모든 정점을 찾는" 시간복잡도, 그리고 공간복잡도를 비교해 주세요.
두 정점이 연결되었는지 확인하는 시간복잡도
배열의 경우 인덱스를 이용해 접근하기 때문에 O(1) 만큼 걸리지만 연결리스트는 순회를 필요로 하기 때문에 최악의 경우 O(V)만큼 걸리게 된다.
한 정점에 연결된 모든 정점을 찾는 시간복잡도
배열의 경우 모든 노드를 수노히해야하기 떄문에 O(V)만큼 걸리지만 연결리스트는 O(E)만큼 걸린다.
공간 복잡도
이차원 배열은 O(V^2)의 공간복잡도를 가지나 연결리스트는 O(V+E)의 공간복잡도를 가진다.
정점의 개수가 N개, 간선의 개수가 N^3 개라면, 어떤 방식으로 구현하는 것이 효율적일까요?
간선의 개수가 많기 때문에 배열이 효율적이다.
사이클이 없는 그래프는 모두 트리인가요? 그렇지 않다면, 예시를 들어주세요.
아니요, 방향성이 없는 그래프는 트리가 아닙니다.
그래프에서, 최단거리를 구하는 방법에 대해 설명해 주세요.
그래프의 종류에 따라 BFS(가중치 없는경우), 다익스트라(가중치가 다 양수일 경우), Bellman-ford 알고리즘 등이 있다.
트리에서는 어떤 방식으로 최단거리를 구할 수 있을까요? (위 방법을 사용하지 않고)
LCA를 이용하면 가능하다.
다익스트라 알고리즘에서, 힙을 사용하지 않고 구현한다면 시간복잡도가 어떻게 변화할까요?
O(N^2)으로 변화한다.
정점의 개수가 N개, 간선의 개수가 N^3 개라면, 어떤 알고리즘이 효율적일까요?
- floyd
A* 알고리즘에 대해 설명해 주세요. 이 알고리즘은 다익스트라와 비교해서 어떤 성능을 낼까요?
- 가중치 그래프에서 시작노드에서 목표노드까지의 최단경로만을 구하려는 알고리즘
- f(n) = g(n)+h(n)
- A*가 다익스트라에 비해 빠르다
g(n)은 시작노드부터 현재 노드까지의 비용
h(n)은 휴리스틱 함수라 하여 주로 맨해튼거리나 유클리드 거리를 사용한다.
음수 간선이 있을 때와, 음수 사이클이 있을 때 각각 어떤 최단거리 알고리즘을 사용해야 하는지 설명해 주세요.
음수 간선이 있을시 floyd나 bellman을 사용하면 된다. 음수 사이클이 있으시에는 어떠한 알고리즘도 작동하지 않는다.
참고자료