재귀함수에 대해 설명해 주세요.

재귀함수란 함수안에서 자기 자신을 호출하는 함수를 의미한다.

재귀 함수의 동작 과정을 Call Stack을 활용해서 설명해 주세요.

재귀함수의 동작은 stack에 함수가 계속 쌓여가다가 return을 시작하면서 stack에서 다시 쌓였던 함수를 call하며 최종 결과를 도출한다.

언어의 스펙에 따라, 재귀함수의 최적화를 진행해주는 경우가 있습니다. 어떤 경우에 재귀함수의 최적화가 가능하며, 이를 어떻게 최적화 할 수 있을지 설명해 주세요.

꼬리 재귀

반환값에서 추가적인 연산을 수행하지 않도록 구현해 스택을 재활용할 수 있게 한다.

MST가 무엇이고, 어떻게 구할 수 있을지 설명해 주세요.

Minimum cost Spanning Tree를 의미하고 버텍스가 n개 있을 때 n-1개의 엣지로 모두 연결되어 있으며 사이클이 없고 가중치의 합이 최소가 되는 Spanning Tree를 의미한다. Kruskal 알고리즘등을 사용할 수 있다.

Kruskal 알고리즘에서 사용하는 Union-Find 자료구조에 대해 설명해 주세요.

합집합을 찾는 구조이고, 버텍스에 라벨을 붙여서 라벨이 같다면 같은 그래프에 속하는 것으로 판단하고, 아니라면 다른 그래프에 속하는 것으로 판단하는 알고리즘이다.

Kruskal 과 Prim 중, 어떤 것이 더 빠를까요?

• Kruskal: 간선을 정렬하고 순서대로 연결, Union-Find 상수 시간이기 때문에 O(ElogE)
• Prim : 모든 노드에 대해 최소간선을 찾는 시간 O(VlogV) + 각 노드의 인접 간선을 찾아 힙에 넣는 시간 O(ElogV) = O(ElogV)

  일반적으로 E가 V보다 크기 때문

그래프 내 간선이 많은 경우 프림, 간선이 적은 경우 kruskal이 빠르다.

Thread Safe 한 자료구조가 있을까요? 없다면, 어떻게 Thread Safe 하게 구성할 수 있을까요?

없다, mutex lock을 걸거나, 세마포어, swift라면 gcd를 이용해서 구현해야한다.

배열의 길이를 알고 있다면, 조금 더 빠른 Thread Safe 한 연산을 만들 순 없을까요?

모름

사용하고 있는 언어의 자료구조는 Thread Safe 한가요? 그렇지 않다면, Thread Safe 한 Wrapped Data Structure 를 제공하고 있나요?

아니요. swift 는 thread safe를 고려하고 만든 언어가 아닙니다. Wrapped Data structure는 없으나 Actor라는 스레드 안정성을 보장하는 타입이 존재한다.

문자열을 저장하고, 처리하는 주요 자료구조 및 알고리즘 (Trie, KMP, Rabin Karp 등) 에 대해 설명해 주세요.

Trie

• 문자열의 집합을 표현하는 트리 자료구조
• K진 트리 구조를 통해 문자열을 저장
• O(M)의 시간으로 문자열 탐색 가능

KMP

• failure function을 이용해 비교

• O(n+m)시간으로 탐색 가능

• 패턴을 정의해서 했던 비교를 다시하지 않는다
  
  
  

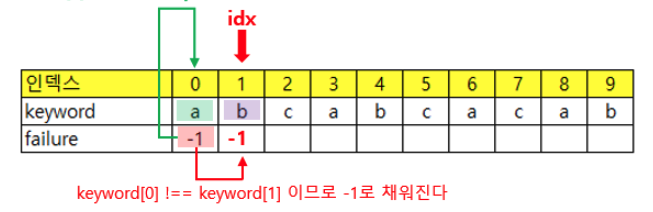
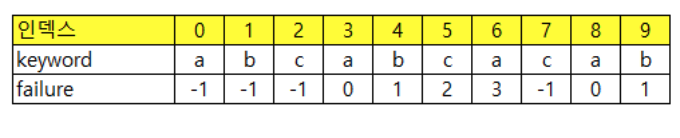
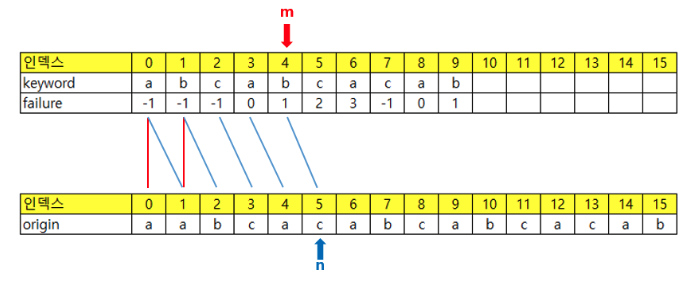
• 키워드와 origin이 달라졌을 때 n의 값은 현재 m의 값의 한 칸 앞의 failure 값에 1을 더한 값이 된다.

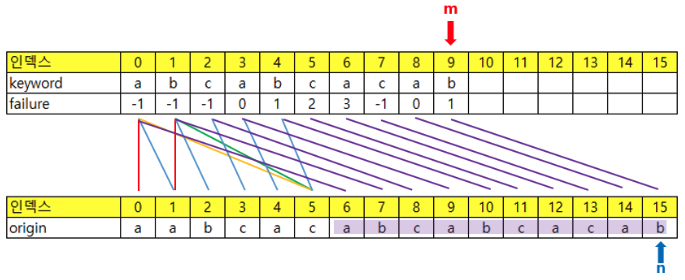
Rabin-Karp

• 해시값을 이용해 문자열 비교
• 해시값이 같더라도 문자열이 다를 수 있기 때문에 해시값이 같을 경우 문자열 자체를 비교함

  Spurious Hit

• 해시함수는 $\Sigma_{i=0}^nm_ix^{n-i}$을 사용하며 표현범위를 초과할 때를 대비해 나머지 연산을 하기도 한다.

  m: 아스키 코드 값
  x: 소수, 일반적으로 2
  n: 문자열 길이

• rolling hash를 통해 최적화

  틀렸을 시 hash = 2*(기존 해쉬 - 맨 앞 문에 대한 해쉬 값) + 새로 들어온 문자

• O(M+N)의 시간복잡도

이진탐색이 무엇인지 설명하고, 시간복잡도를 증명해 보세요.

중간에 있는 임의의 값을 선택하여 찾고자하는 값이 크다면 오른쪽 작다면 왼쪽으로 이하여 탐색한다. 동일한 방법으로 중간의 값을 선택하고 비교하며 해당 값을 찾을 때 까지 반복한다.

시간 복잡도

N개의 크기의 배열을 이진 탐색한다고 가정했을 때 2씩 나눠 탐색하므로 연산의 수를 K라 가정하면
$2^K = N$
$K = log_2(N)$
따라서 O(logN)

Lower Bound, Upper Bound 는 무엇이고, 이를 어떻게 구현할 수 있을까요?

lower bound

• 찾고자 하는 값 이상이 처음 나타나는 위치
• A[m-1] < k, A[m] >= k를 만족하는 최소 m
• 구간을 잡을 때 [1,N]의 범위가 아닌 [1,N+1]

upper bound

• 찾고자 하는 값보다 큰 값이 처음으로 나타나는 위치
• A[m-1]<=k, A[m]>k를 만족하는 최소 m
• 구간을 잡을 때 [1,N]의 범위가 아닌 [1,N+1]

이진탐색의 논리를 적용하여 삼진탐색을 작성한다고 가정한다면, 시간복잡도는 어떻게 변화할까요? (실제 존재하는 삼진탐색 알고리즘은 무시하세요!)

• 최악의 경우 2개의 기준점을 비교하여 1/3 범위를 줄임
• 이진탐색은 2번 탐색하면 범위가 1/4로 줄여짐
• 이진 탐색 알고리즘이 빠르다.

기존 이진탐색 로직에서 부등호의 범위가 바뀐다면, (ex. <= 라면 <로, <이라면 <= 로) 결과가 달라질까요?

범위의 끝부분을 볼 것인가 말것인가가 달라진다. 예를 들어 배열이 [0,1]이고 1을 찾는다면 end=1이고 start = 0 이기 때문에 반복문이 한번 실행된다 이때 mid = 0이기 때문에 start는 1이되어 반복문의 부등호가 < 라면 종료해 탐색의 실패하고 <=라면 반복문을 한번 더 수행하므로 성공한다.

참고자료

• https://bozeury.tistory.com/96
• https://bowbowbow.tistory.com/26
• https://8iggy.tistory.com/159
• https://ongveloper.tistory.com/376
• https://frtt0608.tistory.com/115
• https://blinders.tistory.com/83
• https://yoongrammer.tistory.com/93
• https://cjh5414.github.io/binary-search/
• https://12bme.tistory.com/120
• https://hojunking.tistory.com/65