Imaging Geometry

Object of Interest in World Coordinate System (U, V, W)
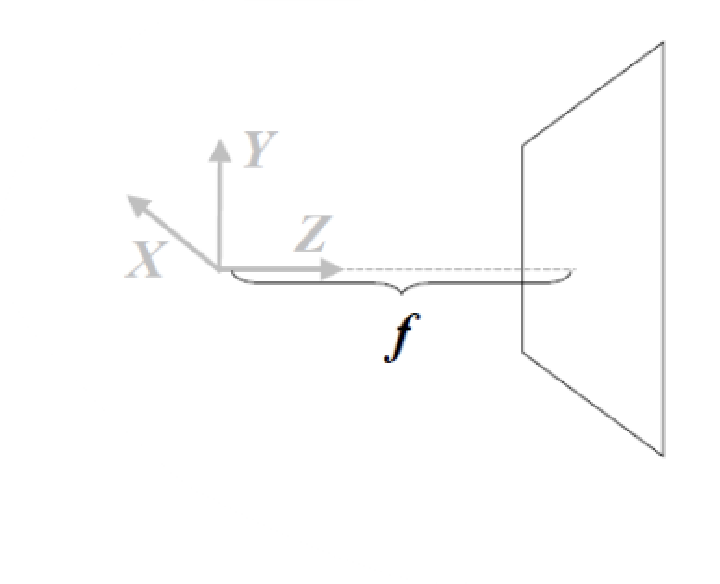
Camera Coordinate System (X, Y, Z)
- f is focal length
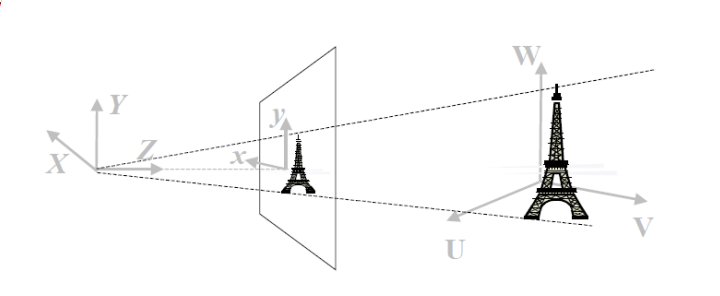
Forward Projection onto image plane 3D (X, Y, Z) projected to 2D (x, y)

Our image gets digitized into pixel coordinates (u, v)
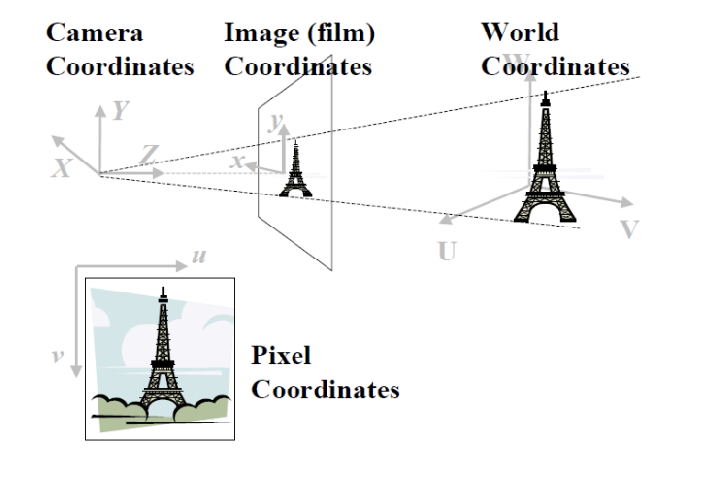
카메라로 촬영을 한다는 것은, 위와 같은 4개의 space을 모두 거친다는 의미이다. 즉, 4개의 좌표계 사이에 3번의 transformation이 발생한다.
Forward Projection
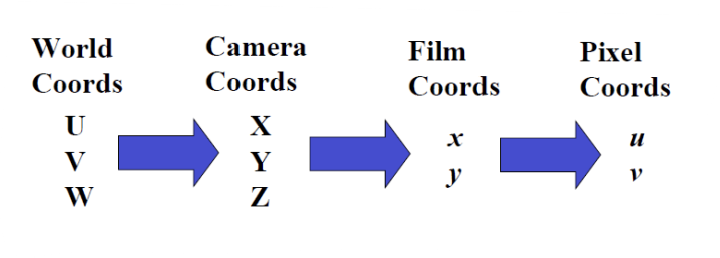
우리는 카메라에 찍힌 이미지를 볼 수 있다. 이렇게 우리가 확인하는 이미지는 Pixel Coordinates 상의 (u, v)이다.
Backward Projection
→ CV가 수행하는 task
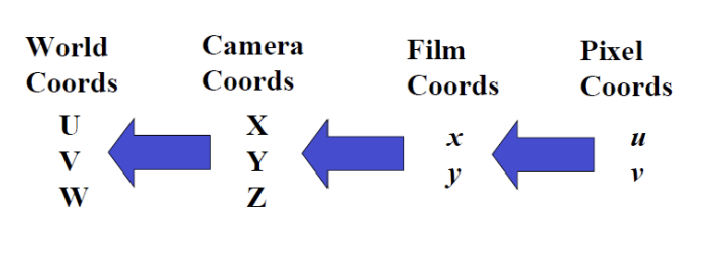
우리는 images(via stereo or motion)으로부터 3D 형상을 reconstruction하기 위해 backward projection을 수행해야 한다.
앗, 근데 backward projection을 수행하기 전에 forward projection부터 알아보자
Forward Projection
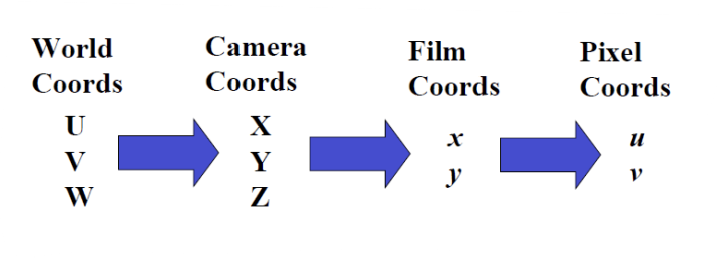
World Coords → Camera Coords 를 확인해보자. (U, V, W) 가 (X, Y, Z)로 변환된다. 이러한 transformation같은 경우, data의 크기와 모양에 왜곡을 주지 않고 진행하는 transformation이다.
이러한 transformation을 Rigid Transformation이라고 한다. Rigid Transformation은 rotation + translation 두 개의 변환만 일어난다.
World to Cmaera Transformation
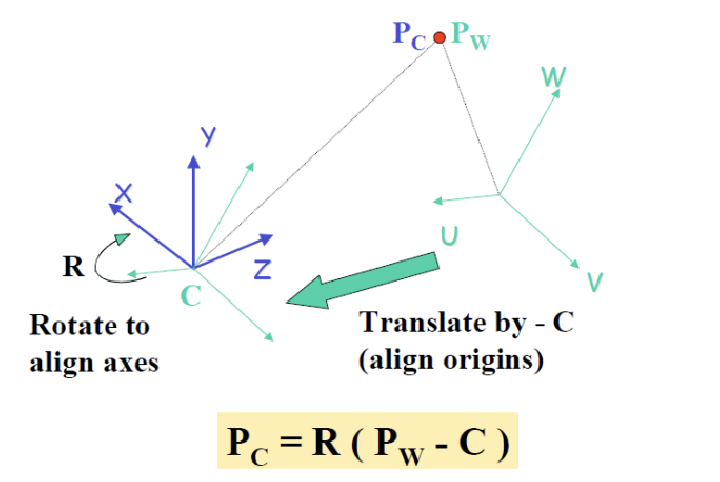
world coordinate를 camera coordinate으로 변환하기 위해서는 translate하고, rotate하기만 하면 됨.
2차원은 한 방향으로 회전 가능하고, 3차원은 세 방향으로 회전 가능하다.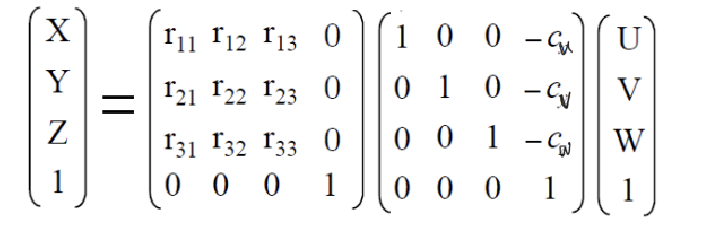
위는 rigid transformation하기 위한 행렬식이다. 먼저 가운데 행렬과 가장 오른쪽 행렬을 보면, 각각에 상수값을 더해주는 translation과정이라고 볼 수 있다. 그리고 왼쪽 행렬은 3차원 공간을 rotation하기 위한 matrix이다.
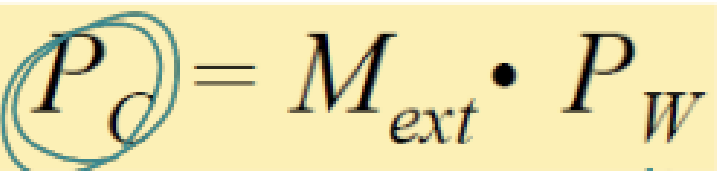
rotation 행렬과 translation 행렬을 하나로 합쳐서 한 번에 계산하자.
Forward Projection
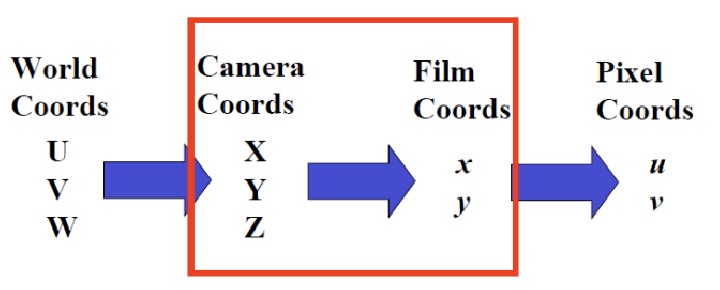
Camera Coords에서 Film Coords로 변환될 때는 projection이 일어난다. 3D-to-3D transformation에서는 데이터 왜곡이 없어서 one-to-one matching이 되는 반면, 이와 같이 3D-to-2D projection에서는 data 손실이 발생한다.
Pinhole Camera Model
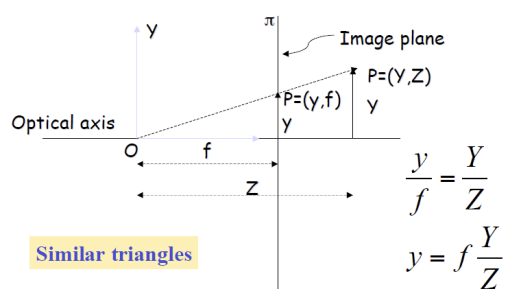
위 사진과 같이 3D를 2D로 변환할 때에는 z축의 모든 점이 2D의 딱 한 점에 모두 모이게 된다.
즉, y / f = Y / Z이다. f는 focal length이므로 이미 알고 있는 값이며, y의 길이도 안다. 따라서 y와 f는 given이다. 그리고 두 삼각형은 닮음이므로, f:y = Z:Y이므로, 비율도 알고 있다.
정리해보면, y = f * Y / Z이다.
Perspective Projection
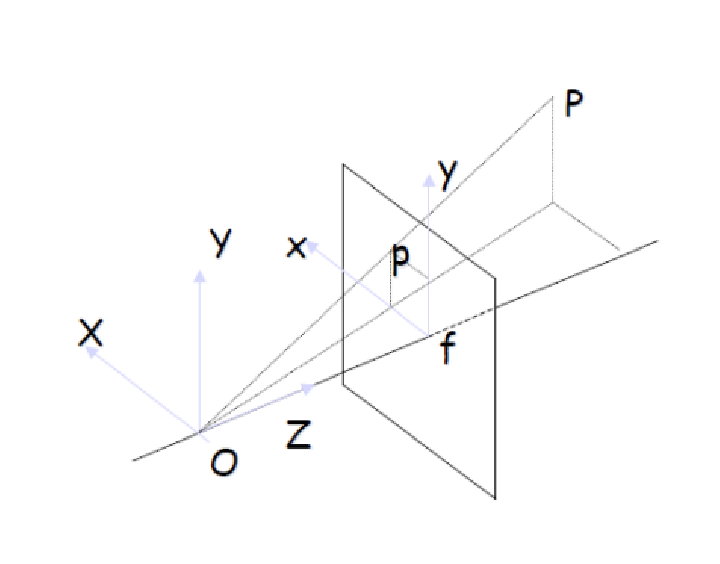
x = f * X / Z, y = f * Y / Z
- Non-linear equation
- Any point on the ray OP has image P(This is a fundamental ambiquity).
Z축에 있는 모든 값들이 image의 한 픽셀 안으로 들어온다. 이것이 바로 근본적인 3D-to-2D projection에 있어 loss가 발생하는 부분이다.
Weak Perspective Approximation
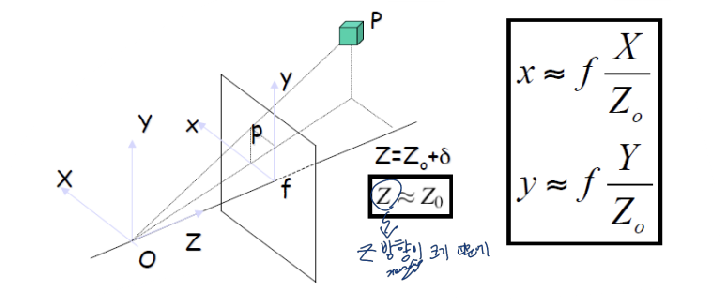
물체와의 거리가 충분히 멀다면(Z값이 크다면), 카메라를 좌우로 움직여도 크게 변하지 않는다. 따라서 좌우 이동에 따른 Z의 변화를 무시하자(== Z를 상수라고 하자).
좌우 이동에 따른 Z 변화를 무시하자는 것이 weak perspective
Perspective Matrix Equation
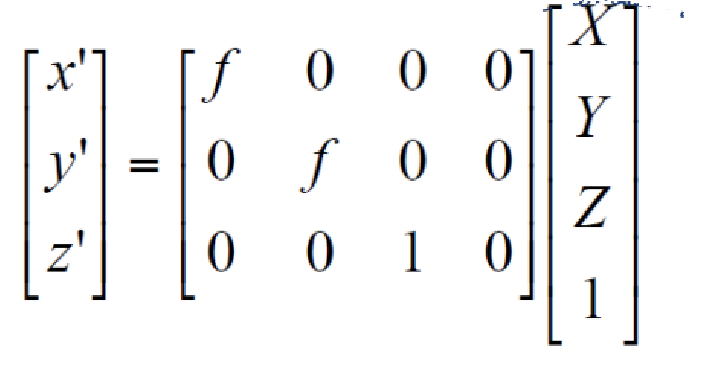
(Using homogeneous coordinates)
- x = f * x / Z
- y = f * Y / Z
homogeneous coordinate이 무엇인가?
3차원 상의 한 점인데, 행렬은 (4x1)이다. 이와 같이 원래 차원 수에 혹이 하나더 붙어있는 coordinate를 homogeneous coordinate이라고 한다.
위 matrix 식과 같이, Z를 1로 만들어서 3D-to-2D transformation을 수행한다.
그런데, 3D-to-2D의 결과라면 3차원상의 한 점이 4x1이고, 마지막 원소가 1이었으니, 위와 같이 transformation하여 나온 결과가 3x1이고, 마지막 원소가 1이어야 하지 않을까?
→ 위처럼 나온 3x1 matrix에 상수를 곱해주면 3x1이며, 마지막 원소를 1로 만들어줄 수 있다. 이렇게 matrix에 상수를 곱한다는 것은, size가 바뀐다는 것을 의미한다.
→ 그럼 이렇게 생각해볼 수 있다. 아, 이 계산은 어떤 상수가 곱해지는 상황을 개의치 않는구나
→ 이게 무슨 말이냐면, 이 세상의 object size를 카메라에 정확하게 담을 수 없다는 의미이다. 카메라로 세상을 담는 순간, '절대 크기'가 사라진다.
3D-to-2D projection이 수행할 때, 크기 정보를 잃는다.
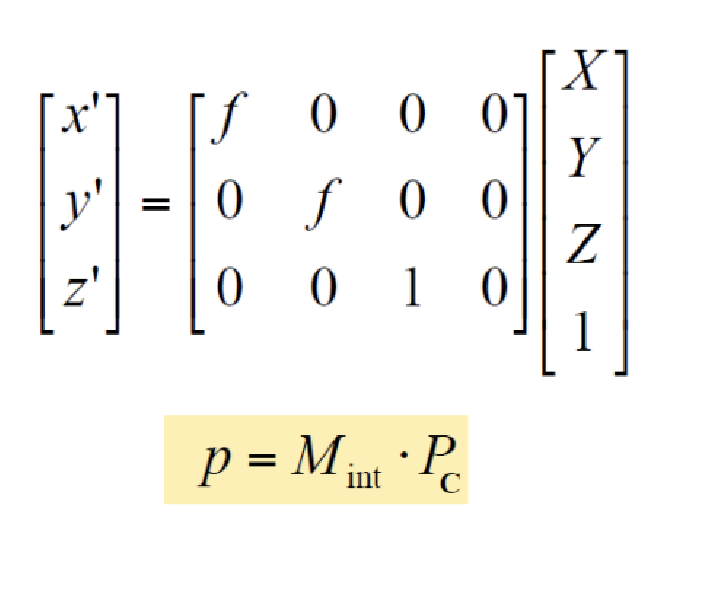
Forward Projection
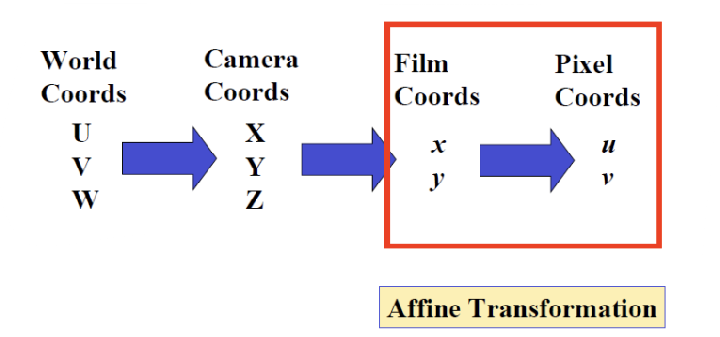
- World Coords → Camera Coords: Rigid Transformation
- Cameara Coords → Film Coords: Perspective Transformation
- Film Coords → Pixel Coords: Affine Transformation
Affine Transformation은 transformation이 발생하긴 하나, 상대적으로 규칙적인 찌그러짐이 발생하는 transformation이다.
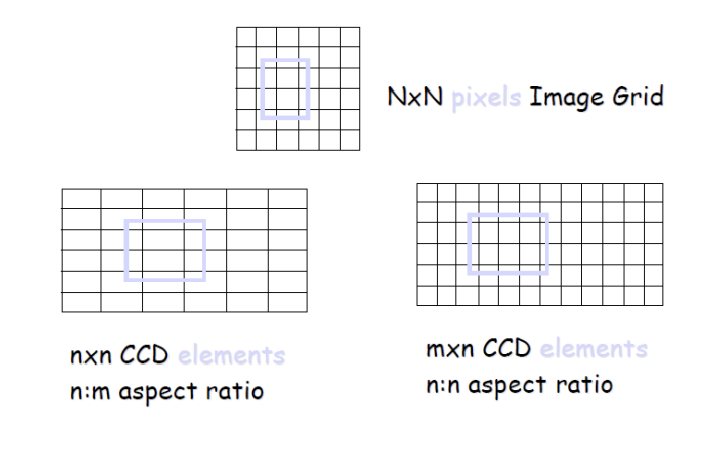
- 센서가 좌우로 늘어져있으면, 사진엔 홀쭉해져서 나온다 → deformation
- 카메라라는 device와 저장된 image 사이의 왜곡을 일으키는 것이 affine transformation이다.
Summary: Forward Projection
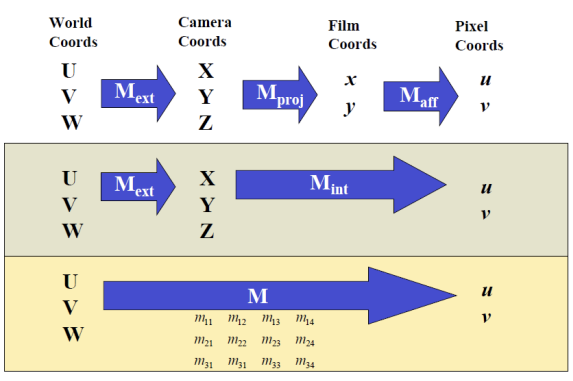
World Coords에서 Camera Coords로 변환되는 과정을 External Transformation이라고도 한다(카메라 외부에서 일어난다고 하여). perspective transformation과 affine transformation을 통틀어 Internval transformation이라고도 한다(카메라 내부에서 일어난다고 하여).
World Coordinate과 Camera Coordinate 사이에는 시점의 이동만 있을 뿐인데, World Coordinate는 왜 있을까 의문이 들 수 있다.
이는 카메라가 여러 대 있을 때, 각각의 카메라의 기준 말고, 하나의 통일된 기준이 된다(사실상 특정 카메라를 기준점이 되기도 한다.)
homogeneous coordinate는 왜 사용할까?
3차원을 원소 1이 추가된 4x1로 표현하는 것을 homogenous coordinate이라고 하였다. 그런데, 왜 이렇게 사용하는 것일까?
이렇게 함으로써 3차원 공간 상의 x, y, z라는 point(점)을 의미한다. vecotr는 3차원 공간 상에 여러 개(방향이 같은) 존재할 수 있기 때문에, 하나의 점을 나타내기 위해 1을 추가한다.
Consider a Line in the World
→ 선도 3D to 2D 해보자.
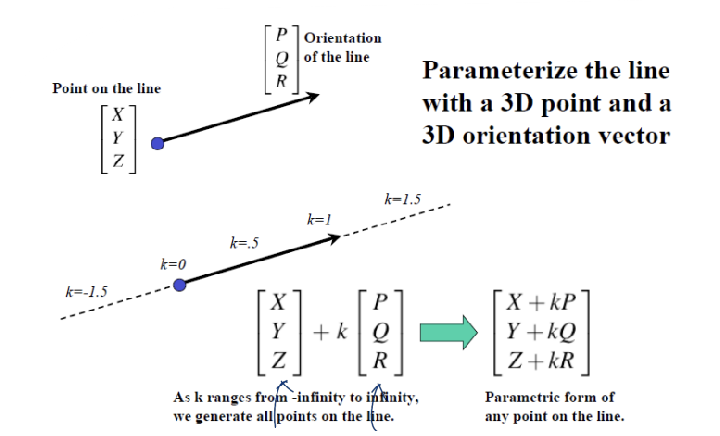
[X, Y, Z]'는 점을 의미하고, [P, Q, R]'은 벡터를 의미한다. 이 두 벡터를 더한다는 의미는, 하나의 point에서 어떤 방향(벡터)으로 갈건데, k만큼 이동하겠다는 것을 의미한다. 이렇게 계산된 결과인 [X + kP, Y + kQ, Z + kR]은 3차원 공간 상의 선을 의미한다.
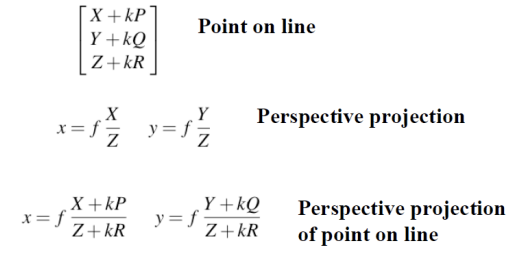
이렇게 계산해보면 다음과 같은 결과가 나온다.
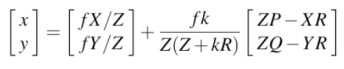
결과적으로, [x, y]는 2차원 상에서의 '선'을 의미하게 된다. 즉, 3차원 상에서의 선을 2차원으로 transformation하여도 선이라는 것을 확인할 수 있다.